2020-2021学年湖南省长沙市雨花区广益八年级(下)期中数学试卷(word解析版)
文档属性
| 名称 | 2020-2021学年湖南省长沙市雨花区广益八年级(下)期中数学试卷(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 786.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 17:20:02 | ||
图片预览




文档简介
2020-2021学年湖南省长沙市雨花区广益八年级(下)期中数学试卷
一、选择题(共12小题,满分36分,每小题3分).
1.函数y=自变量x的取值范围是( )
A.x≥﹣1 B.x≠2 C.x≥﹣1且x≠2 D.﹣1≤x<2
2.下列是一元二次方程的是( )
A.﹣5x+2=1 B.2x2﹣y+1=0 C.x2+2x=0 D.x2﹣=0
3.在“中国汉字听写大赛”选拔赛中,甲,乙两位同学的平均分都是85分,甲的成绩方差是16,乙的成绩方差是5.下列说法正确的是( )
A.甲的成绩比乙的成绩稳定
B.乙的成绩比甲的成绩稳定
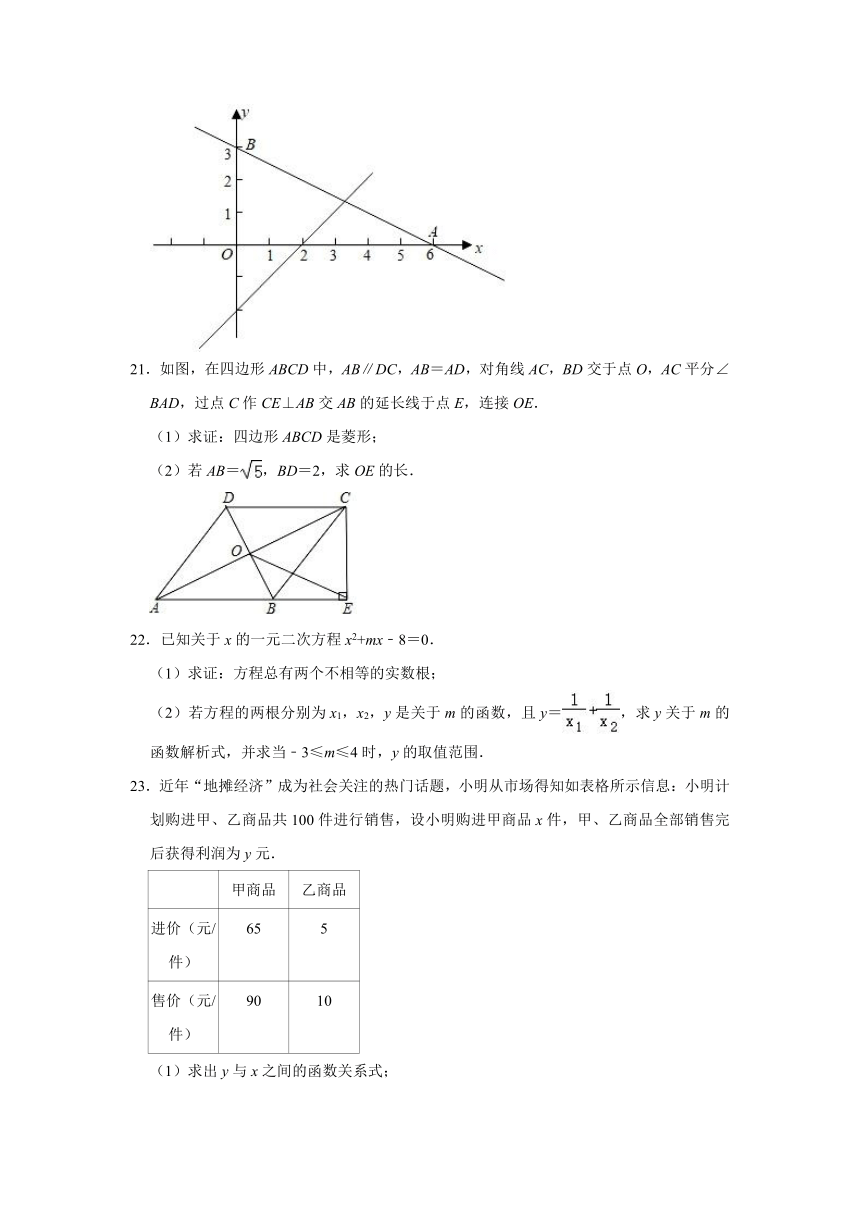
C.甲、乙两人的成绩一样稳定
D.无法确定甲、乙的成绩谁更稳定
4.如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AO=4,则AB的长是( )
A.4 B.5 C.6 D.8
5.最近两年长沙成为了网红城市,岳麓山、橘子洲头、省植物园、省博物馆、世界之窗都深受游客喜爱.某班同学分小组到以上五个地方进行“我爱长沙”主题研学旅行,人数分别为:12,10,11,10,7,这组数据的众数和中位数分别是( )
A.10,10 B.10,11 C.10,12 D.7,11
6.疫情期间,医用物资的运输常常比较棘手,快递小哥甲和的士司机乙同时接到了“将一些药物从江岸区的赵家条运往江夏区的八分山”的任务.已知,两地之间有20km的距离.设他们前进的路程为skm,甲出发后的时间为th,甲,乙前进的路程与时间的函数图象如图.根据图象信息,下列说法正确的是( )
A.乙比甲晚出发1h B.甲比乙晚到3h
C.甲的速度是4km/h D.乙的速度是10km/h
7.用配方法解一元二次方程2x2﹣4x=1,配方后的结果是( )
A.(x﹣1)2= B.(2x﹣1)2=0 C.2(x﹣1)2=1 D.(x+2)2=
8.下列说法中,正确的是( )
A.对角线互相垂直的四边形是菱形
B.对角线相等的四边形是矩形
C.四条边相等的四边形是菱形
D.矩形的对角线一定互相垂直
9.已知一次函数y=kx+b,函数值y随自变量x的增大而减小,且kb<0,则函数y=kx+b的图象大致是( )
A. B.
C. D.
10.在平面直角坐标系中,已知点A(0,2),点B(3,2),正比例函数y=kx(k≠0)的图象恰好经过线段AB的中点.若点C(2,p)在该正比例函数的图象上,则p的值为( )
A. B. C. D.
11.如图,平行四边形ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为8,那么平行四边形ABCD的周长是( )
A.8 B.12 C.16 D.20
12.如图所示,在平面直角坐标系中,函数y=|x﹣1|的图象由一次函数y=x﹣1和y=﹣x+1的图象与x轴的交点及x轴上方的部分组成.根据前面所讲内容,当自变量﹣1≤x≤2时,若函数y=|x﹣a|(其中a为常量)的最小值为a+5,则满足条件的a的值为( )
A.﹣3 B.﹣5 C.7 D.﹣3或﹣5
二、填空题(共4小题满分12分,每小题3分)
13.若一组数据8,6,x,4,7的平均数是6,则这组数据的方差是 .
14.将函数y=﹣3x+3的图象向下平移2个单位,得到的图象的函数表达式是 .
15.如图,已知E点在正方形ABCD的BC边的延长线上,且CE=AC,AE与CD相交于点F,则∠AFC= .
16.如图,直线y=ax+b和y=kx+2与x轴分别交于点A(﹣2,0),点B(2.8,0).则的解集为 .
三、解答题(共9小题,满分72分)
17.计算:.
18.解一元二次方程:
(1)3x2﹣9=0;
(2)2x2﹣4x﹣16=0.
19.近期,学校开展“书香校园”活动,阅览室又购进了一批优质读物.为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成统计表.
学生借阅图书的次数统计表
借阅图书的次数 0次 1次 2次 3次 4次
人数 7 13 a 10 3
请你根据统计图表中的信息,解答下列问题.
(1)a= ;b= ;
(2)求抽取的部分学生一周内平均每人阅读的次数;
(3)我校大概有5000名学生,根据调查结果,估计学生在一周内借阅图书为“3次及3次以上”的人数.
20.平面直角坐标系xOy中,点P的坐标为(m+1,m﹣1).
(1)试判断点P是否在直线l1:y=x﹣2的图象上,并说明理由;
(2)如图,直线l2:y=﹣x+3的图象与x轴、y轴分别相交于点A、B,若点C是l1与l2的交点,点D为l1与x轴的交点,求四边形OBCD的面积.
21.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=,BD=2,求OE的长.
22.已知关于x的一元二次方程x2+mx﹣8=0.
(1)求证:方程总有两个不相等的实数根;
(2)若方程的两根分别为x1,x2,y是关于m的函数,且y=,求y关于m的函数解析式,并求当﹣3≤m≤4时,y的取值范围.
23.近年“地摊经济”成为社会关注的热门话题,小明从市场得知如表格所示信息:小明计划购进甲、乙商品共100件进行销售,设小明购进甲商品x件,甲、乙商品全部销售完后获得利润为y元.
甲商品 乙商品
进价(元/件) 65 5
售价(元/件) 90 10
(1)求出y与x之间的函数关系式;
(2)小明用不超过3500元资金一次性购进甲、乙两种商品,求x的取值范围.
(3)在(2)的条件下,若要求甲,乙商品全部销售完后获得的利润不少于1450元,请说明小明有哪些可行的进货方案,并计算哪种进货方案的利润最大,最大利润是多少?
24.在平面直角坐标系xOy中,对于M、N两点给出如下定义:若点M到x,y轴的距离之和等于点N到x,y轴的距离之和,则称M、N两点为“平等点”,例如:M(1,2)、N(﹣2,﹣1)两点即为“平等点”.
(1)已知点A的坐标为(4,2),
①在点J(﹣2,﹣4)K(3,﹣4)L(3,﹣3)中,为点A的“平等点”的是 .(填字母)
②若点B在y轴上,且A、B两点为“平等点”,则点B的坐标为 .
(2)已知直线y=x+4与x轴、y轴分别交于C、D两点,E为线段CD上一点,F是直线y=3x上的点,若E、F两点为“平等点”,求点F的坐标.
(3)如图,点P(m,n)位于第一象限,且m+n=6,第二象限的点Q为P的“平等点”,且∠POQ=90°,过P、Q两点作x轴的垂线,垂足分别为R、S.若直线y=﹣2x平分四边形PQSR的面积,求直线PQ的解析式.
25.如图,在边长为4的正方形ABCD中,点E,F分别是边BC,CD上的点,且BE=DF=t,连接EF,AC,相交于点O,G为对角线AC延长线上一点.
(1)求证:△AEF是等腰三角形.
(2)当t为何值时,△AEF的周长比△EFC的周长大8.
(3)当四边形AEGF为菱形时,设△AEF的面积为S1,△GFC的面积为S2,求S1﹣S2关于t的函数解析式,并写出当∠EAF=60°时,S1﹣S2的值.
参考答案
一、选择题(共12小题,满分36分,每小题3分)
1.函数y=自变量x的取值范围是( )
A.x≥﹣1 B.x≠2 C.x≥﹣1且x≠2 D.﹣1≤x<2
解:由题意得,x+1≥0,x﹣2≠0,
解得,x≥﹣1且x≠2,
故选:C.
2.下列是一元二次方程的是( )
A.﹣5x+2=1 B.2x2﹣y+1=0 C.x2+2x=0 D.x2﹣=0
解:A、含有一个未知数,不是一元二次方程,故此选项不符合题意;
B、含有两个未知数,不是一元二次方程,故此选项不符合题意;
C、是一元二次方程,故此选项符合题意;
D、含有分式,不是一元二次方程,故此选项不符合题意.
故选:C.
3.在“中国汉字听写大赛”选拔赛中,甲,乙两位同学的平均分都是85分,甲的成绩方差是16,乙的成绩方差是5.下列说法正确的是( )
A.甲的成绩比乙的成绩稳定
B.乙的成绩比甲的成绩稳定
C.甲、乙两人的成绩一样稳定
D.无法确定甲、乙的成绩谁更稳定
解:∵甲,乙两位同学的平均分都是85分,
而甲的成绩方差是16,乙的成绩方差是5,
即甲的成绩方差大于乙的成绩方差,
∴乙的成绩比甲的成绩稳定.
故选:B.
4.如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AO=4,则AB的长是( )
A.4 B.5 C.6 D.8
解:∵四边形ABCD是矩形,
∴AO=OC,BO=OD,AC=BD,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=AO=4,
故选:A.
5.最近两年长沙成为了网红城市,岳麓山、橘子洲头、省植物园、省博物馆、世界之窗都深受游客喜爱.某班同学分小组到以上五个地方进行“我爱长沙”主题研学旅行,人数分别为:12,10,11,10,7,这组数据的众数和中位数分别是( )
A.10,10 B.10,11 C.10,12 D.7,11
解:∵10出现了2次,出现的次数最多,
∴这组数据的众数是10人;
把这些数从小大排列为7,10,10,11,12,
则中位数是10人.
故选:A.
6.疫情期间,医用物资的运输常常比较棘手,快递小哥甲和的士司机乙同时接到了“将一些药物从江岸区的赵家条运往江夏区的八分山”的任务.已知,两地之间有20km的距离.设他们前进的路程为skm,甲出发后的时间为th,甲,乙前进的路程与时间的函数图象如图.根据图象信息,下列说法正确的是( )
A.乙比甲晚出发1h B.甲比乙晚到3h
C.甲的速度是4km/h D.乙的速度是10km/h
解:由图可得,乙比甲晚出发1个小时,故A正确;
甲比乙晚到2个小时,故B错误;
甲的速度是20÷4=5km/h,故C错误;
乙的速度是20÷1=20km/h,故D错误.
故选:A.
7.用配方法解一元二次方程2x2﹣4x=1,配方后的结果是( )
A.(x﹣1)2= B.(2x﹣1)2=0 C.2(x﹣1)2=1 D.(x+2)2=
解:∵2x2﹣4x=1,
∴x2﹣2x=,
则x2﹣2x+1=+1,即(x﹣1)2=,
故选:A.
8.下列说法中,正确的是( )
A.对角线互相垂直的四边形是菱形
B.对角线相等的四边形是矩形
C.四条边相等的四边形是菱形
D.矩形的对角线一定互相垂直
解:A.对角线互相垂直的平行四边形是菱形,故A选项错误;
B、对角线相等的平行四边形是矩形,故B选项错误;
C、四条边相等的四边形是菱形,故C选项正确;
D、矩形的对角线一定相等,但不垂直,故D选项错误;
故选:C.
9.已知一次函数y=kx+b,函数值y随自变量x的增大而减小,且kb<0,则函数y=kx+b的图象大致是( )
A. B.
C. D.
解:∵一次函数y=kx+b,y随着x的增大而减小,
∴k<0,
∴一次函数y=kx+b的图象经过第二、四象限;
∵kb<0,
∴b>0,
∴图象与y轴的交点在x轴上方,
∴一次函数y=kx+b的图象经过第一、二、四象限.
故选:A.
10.在平面直角坐标系中,已知点A(0,2),点B(3,2),正比例函数y=kx(k≠0)的图象恰好经过线段AB的中点.若点C(2,p)在该正比例函数的图象上,则p的值为( )
A. B. C. D.
解:由题意得A,B中点坐标为(,2),
将(,2)代入y=kx得k=.
将点C(2,p)代入y=x得p=.
故选:D.
11.如图,平行四边形ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为8,那么平行四边形ABCD的周长是( )
A.8 B.12 C.16 D.20
解:∵四边形ABCD是平行四边形,
∴AO=CO.
∵OM⊥AC,
∴MA=MC.
∴△CDM周长=MD+MC+CD=MD+MA+CD=AD+DC=8.
∴平行四边形ABCD周长=2(AD+DC)=16.
故选:C.
12.如图所示,在平面直角坐标系中,函数y=|x﹣1|的图象由一次函数y=x﹣1和y=﹣x+1的图象与x轴的交点及x轴上方的部分组成.根据前面所讲内容,当自变量﹣1≤x≤2时,若函数y=|x﹣a|(其中a为常量)的最小值为a+5,则满足条件的a的值为( )
A.﹣3 B.﹣5 C.7 D.﹣3或﹣5
解:对于函数y=|x﹣a|,最小值为a+5.
情形1:a+5=0,
a=﹣5,
∴y=|x+5|,此时x=﹣5时,y有最小值,不符合题意.
情形2:x=﹣1时,有最小值,此时函数y=x﹣a,由题意:﹣1﹣a=a+5,得到a=﹣3.
∴y=|x+3|,符合题意.
情形3:当x=2时,有最小值,此时函数y=﹣x+a,由题意:﹣2+a=a+5,方程无解,此种情形不存在,
综上所述,a=﹣3.
故选:A.
二、填空题(共4小题满分12分,每小题3分)
13.若一组数据8,6,x,4,7的平均数是6,则这组数据的方差是 2 .
解:∵数据8,6,x,4,7的平均数是6,
∴=6,
解得:x=5,
这组数据的方差是S2=×[(8﹣6)2+(6﹣6)2+(5﹣6)2+(4﹣6)2+(7﹣6)2]=2,
故答案为:2.
14.将函数y=﹣3x+3的图象向下平移2个单位,得到的图象的函数表达式是 y=﹣3x+1 .
解:由“上加下减”的原则可知,把一次函数y=2x+1的图象向下平移1个单位后所得直线的解析式为:y=﹣3x+3﹣2,即y=﹣3x+1.
故答案是:y=﹣3x+1.
15.如图,已知E点在正方形ABCD的BC边的延长线上,且CE=AC,AE与CD相交于点F,则∠AFC= 112.5° .
解:∵CE=AC,
∴∠E=∠CAE,
∵AC是正方形ABCD的对角线,
∴∠ACB=45°,
∴∠E+∠CAE=45°,
∴∠E=×45°=22.5°,
在△CEF中,∠AFC=∠E+∠ECF=22.5°+90°=112.5°.
故答案为:112.5°.
16.如图,直线y=ax+b和y=kx+2与x轴分别交于点A(﹣2,0),点B(2.8,0).则的解集为 x>2.8 .
解:由图象可得,
y=ax+b中y随x的增大而增大,与x轴交于点A(﹣2,0),
y=kx+2中y随x的增大而减小,与x轴交于点B(2.8,0),
∴ax+b>0的解集是x>﹣2,kx+2<0的解集是x>2.8,
∴的解集为x>2.8,
故答案为:x>2.8.
三、解答题(共9小题,满分72分)
17.计算:.
解:原式=1+2+﹣1+3
=5+.
18.解一元二次方程:
(1)3x2﹣9=0;
(2)2x2﹣4x﹣16=0.
解:(1)∵3x2﹣9=0,
∴3x2=9,
则x2=3,
∴x1=,x2=﹣;
(2)∵2x2﹣4x﹣16=0,
∴x2﹣2x﹣8=0,
则(x﹣4)(x+2)=0,
∴x﹣4=0或x+2=0,
解得x1=4,x2=﹣2.
19.近期,学校开展“书香校园”活动,阅览室又购进了一批优质读物.为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成统计表.
学生借阅图书的次数统计表
借阅图书的次数 0次 1次 2次 3次 4次
人数 7 13 a 10 3
请你根据统计图表中的信息,解答下列问题.
(1)a= 17 ;b= 20 ;
(2)求抽取的部分学生一周内平均每人阅读的次数;
(3)我校大概有5000名学生,根据调查结果,估计学生在一周内借阅图书为“3次及3次以上”的人数.
解:(1)本次调查的人数为诶:13÷26%=50,
a=50﹣7﹣13﹣10﹣3=17,b%=10÷50×100%=20%,
故答案为:17,20;
(2)==1.78(次),
即抽取的部分学生一周内平均每人阅读的次数为1.78;
(3)5000×=1300(人),
即估计学生在一周内借阅图书为“3次及3次以上”的有1300人.
20.平面直角坐标系xOy中,点P的坐标为(m+1,m﹣1).
(1)试判断点P是否在直线l1:y=x﹣2的图象上,并说明理由;
(2)如图,直线l2:y=﹣x+3的图象与x轴、y轴分别相交于点A、B,若点C是l1与l2的交点,点D为l1与x轴的交点,求四边形OBCD的面积.
解:(1)∵当x=m+1时,y=m+1﹣2=m﹣1,
∴点P(m+1,m﹣1)在函数y=x﹣2图象上.
(2)∵直线l2:y=﹣x+3的图象与x轴、y轴分别相交于点A、B,
∴A(6,0),B(0,3),
直线l1:y=x﹣2中,令y=0,则x=2,
∴D(2,0),
解得,
∴C(,),
∴S四边形OBCD=S△AOB﹣S△ACD=﹣=.
21.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=,BD=2,求OE的长.
解:(1)∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴?ABCD是菱形;
(2)∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴OB=BD=1,
在Rt△AOB中,AB=,OB=1,
∴OA==2,
∴OE=OA=2.
22.已知关于x的一元二次方程x2+mx﹣8=0.
(1)求证:方程总有两个不相等的实数根;
(2)若方程的两根分别为x1,x2,y是关于m的函数,且y=,求y关于m的函数解析式,并求当﹣3≤m≤4时,y的取值范围.
解:(1)∵Δ=m2﹣4×(﹣8)=m2+32>0,
∴方程有两个不相等的实数根;
(2)∵方程的两根分别为x1,x2,
∴x1+x2=﹣m,x1x2=﹣8,
∴y===,
∴y是关于m的反比例函数,
∵当m=﹣3时,y=﹣,
当m=4时,y=,
∴当﹣3≤m≤4时,y的取值范围是:y≤﹣或y≥.
23.近年“地摊经济”成为社会关注的热门话题,小明从市场得知如表格所示信息:小明计划购进甲、乙商品共100件进行销售,设小明购进甲商品x件,甲、乙商品全部销售完后获得利润为y元.
甲商品 乙商品
进价(元/件) 65 5
售价(元/件) 90 10
(1)求出y与x之间的函数关系式;
(2)小明用不超过3500元资金一次性购进甲、乙两种商品,求x的取值范围.
(3)在(2)的条件下,若要求甲,乙商品全部销售完后获得的利润不少于1450元,请说明小明有哪些可行的进货方案,并计算哪种进货方案的利润最大,最大利润是多少?
解:(1)由题意可得:y=(90﹣65)x+(10﹣5)(100﹣x)=20x+500;
(2)由题意可得:65x+5(100﹣x)≤3500,
解得:x≤50,
又∵x≥0,
∴0≤x≤50;
(3)由题意可得:(90﹣65)x+(10﹣5)(100﹣x)≥1450,
解得:x≥47.5,
∴47.5≤x≤50,
又∵x为整数,
∴x=48,49,50,
∴进货方案有:甲商品进48件,乙商品进52件;甲商品进49件,乙商品进51件;甲商品进50件,乙商品进50件;
∵y=20x+500,
∴y随x的增大而增大,
∴当x=50时,有最大利润.
∴当甲商品进50件,乙商品进50件,利润有最大值.
∴利润最大值为20×50+500=1500(元).
答:进货方案有:甲商品进48件,乙商品进52件;甲商品进49件,乙商品进51件;甲商品进50件,乙商品进50件;甲商品进50件,乙商品进50件利润最大,最大利润是1500元.
24.在平面直角坐标系xOy中,对于M、N两点给出如下定义:若点M到x,y轴的距离之和等于点N到x,y轴的距离之和,则称M、N两点为“平等点”,例如:M(1,2)、N(﹣2,﹣1)两点即为“平等点”.
(1)已知点A的坐标为(4,2),
①在点J(﹣2,﹣4)K(3,﹣4)L(3,﹣3)中,为点A的“平等点”的是 J、L .(填字母)
②若点B在y轴上,且A、B两点为“平等点”,则点B的坐标为 (0,6)或(0,﹣6) .
(2)已知直线y=x+4与x轴、y轴分别交于C、D两点,E为线段CD上一点,F是直线y=3x上的点,若E、F两点为“平等点”,求点F的坐标.
(3)如图,点P(m,n)位于第一象限,且m+n=6,第二象限的点Q为P的“平等点”,且∠POQ=90°,过P、Q两点作x轴的垂线,垂足分别为R、S.若直线y=﹣2x平分四边形PQSR的面积,求直线PQ的解析式.
解:(1)①由点A的坐标知,若点A到x,y轴的距离之和为6,
符合这个条件的点由J、L,
故答案为:J、L;
②设点B的坐标为(0,m),由题意得:0+|m|=4+2,
解得m=±6,
故点B的坐标为(0,6)或(0,﹣6),
故答案为:(0,6)或(0,﹣6);
(2)设点E的坐标为(s,t),则s+t=4,即点E的坐标为(s,4+s),设点F的坐标为(f,3f),
由题意得:﹣s+s+4=4=|f|+|3f|,
解得:f=1或﹣1,
故点F的坐标为(1,3)或(﹣1,﹣3);
(3)∵∠POR+∠QOS=90°,∠POR=∠OPR=90°,
∴∠QOS=∠OPR,
∵∠PRO=∠OSQ=90°,
∴△PRO∽△OSQ,
则上述两个三角形的周长比等于相似比,而两个三角形均为直角三角形,则相似比也等于两个直角边和的比,而两个直角边和相等,故两个直角边相等,故△PRO≌△OSQ(SAS),
∴OS=PR,OR=QS,OP=OQ,
则△OSQ相等于△ORP围绕点O逆时针旋转了90°,
∵点P(m,n)位于第一象限,且m+n=6,即点P的坐标为(m,6﹣m),则点Q的坐标为(m﹣6,m),
由点P、Q的坐标得,直线PQ的表达式为y=(x﹣m)+6﹣m,
∵直线y=﹣2x平分四边形PQSR的面积,则该直线是PQ的中垂线,
故设直线PQ的表达式为y=x+r,
即=,解得m=,
则直线PQ的表达式为y=(x﹣m)+6﹣m=x+.
25.如图,在边长为4的正方形ABCD中,点E,F分别是边BC,CD上的点,且BE=DF=t,连接EF,AC,相交于点O,G为对角线AC延长线上一点.
(1)求证:△AEF是等腰三角形.
(2)当t为何值时,△AEF的周长比△EFC的周长大8.
(3)当四边形AEGF为菱形时,设△AEF的面积为S1,△GFC的面积为S2,求S1﹣S2关于t的函数解析式,并写出当∠EAF=60°时,S1﹣S2的值.
解:(1)证明:由正方形ABCD可知AB=AD,∠ABE=∠ADF=90°,
在Rt△ABE与△ADF中,由勾股定理得:
AE=,AF=,
又BE=DF=t,
∴AE=AF,
∴△AEF是等腰三角形;
(2)C△AEF=AE+EF+AF,C△EFC=CE+EF+CF,
∴C△AEF﹣C△EFC=AE+AF﹣CE﹣CF,
又∵AE=AF,CE=CF,
∴C△AEF﹣C△CEF=2AE﹣2CE=2(AE﹣CE)=2(),
当C△AEF﹣C△CEF=8时,有2()=8,(0<t<4),
解得t=3;
(3)四边形AEQF为菱形,则有S△EFG=S△AEF=S1,对角线AG与EF互相垂直平分,
S△GFC=S2=S△GFO﹣S△CFO=﹣,
∴S1﹣S2=S△AEF﹣S△GFC,
=S△AEF﹣(﹣)
=+
=6﹣4t﹣×(4﹣t)2]+
=8﹣2t,
当∠EAF=60°时,△AEF是等边三角形,
∴∠BAE=15°,
在AB边上取点H,使AH=HE,
则∠BHE=30°,
∴HE=2t,BH=,
∴2t+=4,
解得t=8﹣4.
∴S1﹣S2=8﹣2(8﹣4)=8﹣8.
一、选择题(共12小题,满分36分,每小题3分).
1.函数y=自变量x的取值范围是( )
A.x≥﹣1 B.x≠2 C.x≥﹣1且x≠2 D.﹣1≤x<2
2.下列是一元二次方程的是( )
A.﹣5x+2=1 B.2x2﹣y+1=0 C.x2+2x=0 D.x2﹣=0
3.在“中国汉字听写大赛”选拔赛中,甲,乙两位同学的平均分都是85分,甲的成绩方差是16,乙的成绩方差是5.下列说法正确的是( )
A.甲的成绩比乙的成绩稳定
B.乙的成绩比甲的成绩稳定
C.甲、乙两人的成绩一样稳定
D.无法确定甲、乙的成绩谁更稳定
4.如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AO=4,则AB的长是( )
A.4 B.5 C.6 D.8
5.最近两年长沙成为了网红城市,岳麓山、橘子洲头、省植物园、省博物馆、世界之窗都深受游客喜爱.某班同学分小组到以上五个地方进行“我爱长沙”主题研学旅行,人数分别为:12,10,11,10,7,这组数据的众数和中位数分别是( )
A.10,10 B.10,11 C.10,12 D.7,11
6.疫情期间,医用物资的运输常常比较棘手,快递小哥甲和的士司机乙同时接到了“将一些药物从江岸区的赵家条运往江夏区的八分山”的任务.已知,两地之间有20km的距离.设他们前进的路程为skm,甲出发后的时间为th,甲,乙前进的路程与时间的函数图象如图.根据图象信息,下列说法正确的是( )
A.乙比甲晚出发1h B.甲比乙晚到3h
C.甲的速度是4km/h D.乙的速度是10km/h
7.用配方法解一元二次方程2x2﹣4x=1,配方后的结果是( )
A.(x﹣1)2= B.(2x﹣1)2=0 C.2(x﹣1)2=1 D.(x+2)2=
8.下列说法中,正确的是( )
A.对角线互相垂直的四边形是菱形
B.对角线相等的四边形是矩形
C.四条边相等的四边形是菱形
D.矩形的对角线一定互相垂直
9.已知一次函数y=kx+b,函数值y随自变量x的增大而减小,且kb<0,则函数y=kx+b的图象大致是( )
A. B.
C. D.
10.在平面直角坐标系中,已知点A(0,2),点B(3,2),正比例函数y=kx(k≠0)的图象恰好经过线段AB的中点.若点C(2,p)在该正比例函数的图象上,则p的值为( )
A. B. C. D.
11.如图,平行四边形ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为8,那么平行四边形ABCD的周长是( )
A.8 B.12 C.16 D.20
12.如图所示,在平面直角坐标系中,函数y=|x﹣1|的图象由一次函数y=x﹣1和y=﹣x+1的图象与x轴的交点及x轴上方的部分组成.根据前面所讲内容,当自变量﹣1≤x≤2时,若函数y=|x﹣a|(其中a为常量)的最小值为a+5,则满足条件的a的值为( )
A.﹣3 B.﹣5 C.7 D.﹣3或﹣5
二、填空题(共4小题满分12分,每小题3分)
13.若一组数据8,6,x,4,7的平均数是6,则这组数据的方差是 .
14.将函数y=﹣3x+3的图象向下平移2个单位,得到的图象的函数表达式是 .
15.如图,已知E点在正方形ABCD的BC边的延长线上,且CE=AC,AE与CD相交于点F,则∠AFC= .
16.如图,直线y=ax+b和y=kx+2与x轴分别交于点A(﹣2,0),点B(2.8,0).则的解集为 .
三、解答题(共9小题,满分72分)
17.计算:.
18.解一元二次方程:
(1)3x2﹣9=0;
(2)2x2﹣4x﹣16=0.
19.近期,学校开展“书香校园”活动,阅览室又购进了一批优质读物.为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成统计表.
学生借阅图书的次数统计表
借阅图书的次数 0次 1次 2次 3次 4次
人数 7 13 a 10 3
请你根据统计图表中的信息,解答下列问题.
(1)a= ;b= ;
(2)求抽取的部分学生一周内平均每人阅读的次数;
(3)我校大概有5000名学生,根据调查结果,估计学生在一周内借阅图书为“3次及3次以上”的人数.
20.平面直角坐标系xOy中,点P的坐标为(m+1,m﹣1).
(1)试判断点P是否在直线l1:y=x﹣2的图象上,并说明理由;
(2)如图,直线l2:y=﹣x+3的图象与x轴、y轴分别相交于点A、B,若点C是l1与l2的交点,点D为l1与x轴的交点,求四边形OBCD的面积.
21.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=,BD=2,求OE的长.
22.已知关于x的一元二次方程x2+mx﹣8=0.
(1)求证:方程总有两个不相等的实数根;
(2)若方程的两根分别为x1,x2,y是关于m的函数,且y=,求y关于m的函数解析式,并求当﹣3≤m≤4时,y的取值范围.
23.近年“地摊经济”成为社会关注的热门话题,小明从市场得知如表格所示信息:小明计划购进甲、乙商品共100件进行销售,设小明购进甲商品x件,甲、乙商品全部销售完后获得利润为y元.
甲商品 乙商品
进价(元/件) 65 5
售价(元/件) 90 10
(1)求出y与x之间的函数关系式;
(2)小明用不超过3500元资金一次性购进甲、乙两种商品,求x的取值范围.
(3)在(2)的条件下,若要求甲,乙商品全部销售完后获得的利润不少于1450元,请说明小明有哪些可行的进货方案,并计算哪种进货方案的利润最大,最大利润是多少?
24.在平面直角坐标系xOy中,对于M、N两点给出如下定义:若点M到x,y轴的距离之和等于点N到x,y轴的距离之和,则称M、N两点为“平等点”,例如:M(1,2)、N(﹣2,﹣1)两点即为“平等点”.
(1)已知点A的坐标为(4,2),
①在点J(﹣2,﹣4)K(3,﹣4)L(3,﹣3)中,为点A的“平等点”的是 .(填字母)
②若点B在y轴上,且A、B两点为“平等点”,则点B的坐标为 .
(2)已知直线y=x+4与x轴、y轴分别交于C、D两点,E为线段CD上一点,F是直线y=3x上的点,若E、F两点为“平等点”,求点F的坐标.
(3)如图,点P(m,n)位于第一象限,且m+n=6,第二象限的点Q为P的“平等点”,且∠POQ=90°,过P、Q两点作x轴的垂线,垂足分别为R、S.若直线y=﹣2x平分四边形PQSR的面积,求直线PQ的解析式.
25.如图,在边长为4的正方形ABCD中,点E,F分别是边BC,CD上的点,且BE=DF=t,连接EF,AC,相交于点O,G为对角线AC延长线上一点.
(1)求证:△AEF是等腰三角形.
(2)当t为何值时,△AEF的周长比△EFC的周长大8.
(3)当四边形AEGF为菱形时,设△AEF的面积为S1,△GFC的面积为S2,求S1﹣S2关于t的函数解析式,并写出当∠EAF=60°时,S1﹣S2的值.
参考答案
一、选择题(共12小题,满分36分,每小题3分)
1.函数y=自变量x的取值范围是( )
A.x≥﹣1 B.x≠2 C.x≥﹣1且x≠2 D.﹣1≤x<2
解:由题意得,x+1≥0,x﹣2≠0,
解得,x≥﹣1且x≠2,
故选:C.
2.下列是一元二次方程的是( )
A.﹣5x+2=1 B.2x2﹣y+1=0 C.x2+2x=0 D.x2﹣=0
解:A、含有一个未知数,不是一元二次方程,故此选项不符合题意;
B、含有两个未知数,不是一元二次方程,故此选项不符合题意;
C、是一元二次方程,故此选项符合题意;
D、含有分式,不是一元二次方程,故此选项不符合题意.
故选:C.
3.在“中国汉字听写大赛”选拔赛中,甲,乙两位同学的平均分都是85分,甲的成绩方差是16,乙的成绩方差是5.下列说法正确的是( )
A.甲的成绩比乙的成绩稳定
B.乙的成绩比甲的成绩稳定
C.甲、乙两人的成绩一样稳定
D.无法确定甲、乙的成绩谁更稳定
解:∵甲,乙两位同学的平均分都是85分,
而甲的成绩方差是16,乙的成绩方差是5,
即甲的成绩方差大于乙的成绩方差,
∴乙的成绩比甲的成绩稳定.
故选:B.
4.如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AO=4,则AB的长是( )
A.4 B.5 C.6 D.8
解:∵四边形ABCD是矩形,
∴AO=OC,BO=OD,AC=BD,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=AO=4,
故选:A.
5.最近两年长沙成为了网红城市,岳麓山、橘子洲头、省植物园、省博物馆、世界之窗都深受游客喜爱.某班同学分小组到以上五个地方进行“我爱长沙”主题研学旅行,人数分别为:12,10,11,10,7,这组数据的众数和中位数分别是( )
A.10,10 B.10,11 C.10,12 D.7,11
解:∵10出现了2次,出现的次数最多,
∴这组数据的众数是10人;
把这些数从小大排列为7,10,10,11,12,
则中位数是10人.
故选:A.
6.疫情期间,医用物资的运输常常比较棘手,快递小哥甲和的士司机乙同时接到了“将一些药物从江岸区的赵家条运往江夏区的八分山”的任务.已知,两地之间有20km的距离.设他们前进的路程为skm,甲出发后的时间为th,甲,乙前进的路程与时间的函数图象如图.根据图象信息,下列说法正确的是( )
A.乙比甲晚出发1h B.甲比乙晚到3h
C.甲的速度是4km/h D.乙的速度是10km/h
解:由图可得,乙比甲晚出发1个小时,故A正确;
甲比乙晚到2个小时,故B错误;
甲的速度是20÷4=5km/h,故C错误;
乙的速度是20÷1=20km/h,故D错误.
故选:A.
7.用配方法解一元二次方程2x2﹣4x=1,配方后的结果是( )
A.(x﹣1)2= B.(2x﹣1)2=0 C.2(x﹣1)2=1 D.(x+2)2=
解:∵2x2﹣4x=1,
∴x2﹣2x=,
则x2﹣2x+1=+1,即(x﹣1)2=,
故选:A.
8.下列说法中,正确的是( )
A.对角线互相垂直的四边形是菱形
B.对角线相等的四边形是矩形
C.四条边相等的四边形是菱形
D.矩形的对角线一定互相垂直
解:A.对角线互相垂直的平行四边形是菱形,故A选项错误;
B、对角线相等的平行四边形是矩形,故B选项错误;
C、四条边相等的四边形是菱形,故C选项正确;
D、矩形的对角线一定相等,但不垂直,故D选项错误;
故选:C.
9.已知一次函数y=kx+b,函数值y随自变量x的增大而减小,且kb<0,则函数y=kx+b的图象大致是( )
A. B.
C. D.
解:∵一次函数y=kx+b,y随着x的增大而减小,
∴k<0,
∴一次函数y=kx+b的图象经过第二、四象限;
∵kb<0,
∴b>0,
∴图象与y轴的交点在x轴上方,
∴一次函数y=kx+b的图象经过第一、二、四象限.
故选:A.
10.在平面直角坐标系中,已知点A(0,2),点B(3,2),正比例函数y=kx(k≠0)的图象恰好经过线段AB的中点.若点C(2,p)在该正比例函数的图象上,则p的值为( )
A. B. C. D.
解:由题意得A,B中点坐标为(,2),
将(,2)代入y=kx得k=.
将点C(2,p)代入y=x得p=.
故选:D.
11.如图,平行四边形ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为8,那么平行四边形ABCD的周长是( )
A.8 B.12 C.16 D.20
解:∵四边形ABCD是平行四边形,
∴AO=CO.
∵OM⊥AC,
∴MA=MC.
∴△CDM周长=MD+MC+CD=MD+MA+CD=AD+DC=8.
∴平行四边形ABCD周长=2(AD+DC)=16.
故选:C.
12.如图所示,在平面直角坐标系中,函数y=|x﹣1|的图象由一次函数y=x﹣1和y=﹣x+1的图象与x轴的交点及x轴上方的部分组成.根据前面所讲内容,当自变量﹣1≤x≤2时,若函数y=|x﹣a|(其中a为常量)的最小值为a+5,则满足条件的a的值为( )
A.﹣3 B.﹣5 C.7 D.﹣3或﹣5
解:对于函数y=|x﹣a|,最小值为a+5.
情形1:a+5=0,
a=﹣5,
∴y=|x+5|,此时x=﹣5时,y有最小值,不符合题意.
情形2:x=﹣1时,有最小值,此时函数y=x﹣a,由题意:﹣1﹣a=a+5,得到a=﹣3.
∴y=|x+3|,符合题意.
情形3:当x=2时,有最小值,此时函数y=﹣x+a,由题意:﹣2+a=a+5,方程无解,此种情形不存在,
综上所述,a=﹣3.
故选:A.
二、填空题(共4小题满分12分,每小题3分)
13.若一组数据8,6,x,4,7的平均数是6,则这组数据的方差是 2 .
解:∵数据8,6,x,4,7的平均数是6,
∴=6,
解得:x=5,
这组数据的方差是S2=×[(8﹣6)2+(6﹣6)2+(5﹣6)2+(4﹣6)2+(7﹣6)2]=2,
故答案为:2.
14.将函数y=﹣3x+3的图象向下平移2个单位,得到的图象的函数表达式是 y=﹣3x+1 .
解:由“上加下减”的原则可知,把一次函数y=2x+1的图象向下平移1个单位后所得直线的解析式为:y=﹣3x+3﹣2,即y=﹣3x+1.
故答案是:y=﹣3x+1.
15.如图,已知E点在正方形ABCD的BC边的延长线上,且CE=AC,AE与CD相交于点F,则∠AFC= 112.5° .
解:∵CE=AC,
∴∠E=∠CAE,
∵AC是正方形ABCD的对角线,
∴∠ACB=45°,
∴∠E+∠CAE=45°,
∴∠E=×45°=22.5°,
在△CEF中,∠AFC=∠E+∠ECF=22.5°+90°=112.5°.
故答案为:112.5°.
16.如图,直线y=ax+b和y=kx+2与x轴分别交于点A(﹣2,0),点B(2.8,0).则的解集为 x>2.8 .
解:由图象可得,
y=ax+b中y随x的增大而增大,与x轴交于点A(﹣2,0),
y=kx+2中y随x的增大而减小,与x轴交于点B(2.8,0),
∴ax+b>0的解集是x>﹣2,kx+2<0的解集是x>2.8,
∴的解集为x>2.8,
故答案为:x>2.8.
三、解答题(共9小题,满分72分)
17.计算:.
解:原式=1+2+﹣1+3
=5+.
18.解一元二次方程:
(1)3x2﹣9=0;
(2)2x2﹣4x﹣16=0.
解:(1)∵3x2﹣9=0,
∴3x2=9,
则x2=3,
∴x1=,x2=﹣;
(2)∵2x2﹣4x﹣16=0,
∴x2﹣2x﹣8=0,
则(x﹣4)(x+2)=0,
∴x﹣4=0或x+2=0,
解得x1=4,x2=﹣2.
19.近期,学校开展“书香校园”活动,阅览室又购进了一批优质读物.为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成统计表.
学生借阅图书的次数统计表
借阅图书的次数 0次 1次 2次 3次 4次
人数 7 13 a 10 3
请你根据统计图表中的信息,解答下列问题.
(1)a= 17 ;b= 20 ;
(2)求抽取的部分学生一周内平均每人阅读的次数;
(3)我校大概有5000名学生,根据调查结果,估计学生在一周内借阅图书为“3次及3次以上”的人数.
解:(1)本次调查的人数为诶:13÷26%=50,
a=50﹣7﹣13﹣10﹣3=17,b%=10÷50×100%=20%,
故答案为:17,20;
(2)==1.78(次),
即抽取的部分学生一周内平均每人阅读的次数为1.78;
(3)5000×=1300(人),
即估计学生在一周内借阅图书为“3次及3次以上”的有1300人.
20.平面直角坐标系xOy中,点P的坐标为(m+1,m﹣1).
(1)试判断点P是否在直线l1:y=x﹣2的图象上,并说明理由;
(2)如图,直线l2:y=﹣x+3的图象与x轴、y轴分别相交于点A、B,若点C是l1与l2的交点,点D为l1与x轴的交点,求四边形OBCD的面积.
解:(1)∵当x=m+1时,y=m+1﹣2=m﹣1,
∴点P(m+1,m﹣1)在函数y=x﹣2图象上.
(2)∵直线l2:y=﹣x+3的图象与x轴、y轴分别相交于点A、B,
∴A(6,0),B(0,3),
直线l1:y=x﹣2中,令y=0,则x=2,
∴D(2,0),
解得,
∴C(,),
∴S四边形OBCD=S△AOB﹣S△ACD=﹣=.
21.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=,BD=2,求OE的长.
解:(1)∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴?ABCD是菱形;
(2)∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴OB=BD=1,
在Rt△AOB中,AB=,OB=1,
∴OA==2,
∴OE=OA=2.
22.已知关于x的一元二次方程x2+mx﹣8=0.
(1)求证:方程总有两个不相等的实数根;
(2)若方程的两根分别为x1,x2,y是关于m的函数,且y=,求y关于m的函数解析式,并求当﹣3≤m≤4时,y的取值范围.
解:(1)∵Δ=m2﹣4×(﹣8)=m2+32>0,
∴方程有两个不相等的实数根;
(2)∵方程的两根分别为x1,x2,
∴x1+x2=﹣m,x1x2=﹣8,
∴y===,
∴y是关于m的反比例函数,
∵当m=﹣3时,y=﹣,
当m=4时,y=,
∴当﹣3≤m≤4时,y的取值范围是:y≤﹣或y≥.
23.近年“地摊经济”成为社会关注的热门话题,小明从市场得知如表格所示信息:小明计划购进甲、乙商品共100件进行销售,设小明购进甲商品x件,甲、乙商品全部销售完后获得利润为y元.
甲商品 乙商品
进价(元/件) 65 5
售价(元/件) 90 10
(1)求出y与x之间的函数关系式;
(2)小明用不超过3500元资金一次性购进甲、乙两种商品,求x的取值范围.
(3)在(2)的条件下,若要求甲,乙商品全部销售完后获得的利润不少于1450元,请说明小明有哪些可行的进货方案,并计算哪种进货方案的利润最大,最大利润是多少?
解:(1)由题意可得:y=(90﹣65)x+(10﹣5)(100﹣x)=20x+500;
(2)由题意可得:65x+5(100﹣x)≤3500,
解得:x≤50,
又∵x≥0,
∴0≤x≤50;
(3)由题意可得:(90﹣65)x+(10﹣5)(100﹣x)≥1450,
解得:x≥47.5,
∴47.5≤x≤50,
又∵x为整数,
∴x=48,49,50,
∴进货方案有:甲商品进48件,乙商品进52件;甲商品进49件,乙商品进51件;甲商品进50件,乙商品进50件;
∵y=20x+500,
∴y随x的增大而增大,
∴当x=50时,有最大利润.
∴当甲商品进50件,乙商品进50件,利润有最大值.
∴利润最大值为20×50+500=1500(元).
答:进货方案有:甲商品进48件,乙商品进52件;甲商品进49件,乙商品进51件;甲商品进50件,乙商品进50件;甲商品进50件,乙商品进50件利润最大,最大利润是1500元.
24.在平面直角坐标系xOy中,对于M、N两点给出如下定义:若点M到x,y轴的距离之和等于点N到x,y轴的距离之和,则称M、N两点为“平等点”,例如:M(1,2)、N(﹣2,﹣1)两点即为“平等点”.
(1)已知点A的坐标为(4,2),
①在点J(﹣2,﹣4)K(3,﹣4)L(3,﹣3)中,为点A的“平等点”的是 J、L .(填字母)
②若点B在y轴上,且A、B两点为“平等点”,则点B的坐标为 (0,6)或(0,﹣6) .
(2)已知直线y=x+4与x轴、y轴分别交于C、D两点,E为线段CD上一点,F是直线y=3x上的点,若E、F两点为“平等点”,求点F的坐标.
(3)如图,点P(m,n)位于第一象限,且m+n=6,第二象限的点Q为P的“平等点”,且∠POQ=90°,过P、Q两点作x轴的垂线,垂足分别为R、S.若直线y=﹣2x平分四边形PQSR的面积,求直线PQ的解析式.
解:(1)①由点A的坐标知,若点A到x,y轴的距离之和为6,
符合这个条件的点由J、L,
故答案为:J、L;
②设点B的坐标为(0,m),由题意得:0+|m|=4+2,
解得m=±6,
故点B的坐标为(0,6)或(0,﹣6),
故答案为:(0,6)或(0,﹣6);
(2)设点E的坐标为(s,t),则s+t=4,即点E的坐标为(s,4+s),设点F的坐标为(f,3f),
由题意得:﹣s+s+4=4=|f|+|3f|,
解得:f=1或﹣1,
故点F的坐标为(1,3)或(﹣1,﹣3);
(3)∵∠POR+∠QOS=90°,∠POR=∠OPR=90°,
∴∠QOS=∠OPR,
∵∠PRO=∠OSQ=90°,
∴△PRO∽△OSQ,
则上述两个三角形的周长比等于相似比,而两个三角形均为直角三角形,则相似比也等于两个直角边和的比,而两个直角边和相等,故两个直角边相等,故△PRO≌△OSQ(SAS),
∴OS=PR,OR=QS,OP=OQ,
则△OSQ相等于△ORP围绕点O逆时针旋转了90°,
∵点P(m,n)位于第一象限,且m+n=6,即点P的坐标为(m,6﹣m),则点Q的坐标为(m﹣6,m),
由点P、Q的坐标得,直线PQ的表达式为y=(x﹣m)+6﹣m,
∵直线y=﹣2x平分四边形PQSR的面积,则该直线是PQ的中垂线,
故设直线PQ的表达式为y=x+r,
即=,解得m=,
则直线PQ的表达式为y=(x﹣m)+6﹣m=x+.
25.如图,在边长为4的正方形ABCD中,点E,F分别是边BC,CD上的点,且BE=DF=t,连接EF,AC,相交于点O,G为对角线AC延长线上一点.
(1)求证:△AEF是等腰三角形.
(2)当t为何值时,△AEF的周长比△EFC的周长大8.
(3)当四边形AEGF为菱形时,设△AEF的面积为S1,△GFC的面积为S2,求S1﹣S2关于t的函数解析式,并写出当∠EAF=60°时,S1﹣S2的值.
解:(1)证明:由正方形ABCD可知AB=AD,∠ABE=∠ADF=90°,
在Rt△ABE与△ADF中,由勾股定理得:
AE=,AF=,
又BE=DF=t,
∴AE=AF,
∴△AEF是等腰三角形;
(2)C△AEF=AE+EF+AF,C△EFC=CE+EF+CF,
∴C△AEF﹣C△EFC=AE+AF﹣CE﹣CF,
又∵AE=AF,CE=CF,
∴C△AEF﹣C△CEF=2AE﹣2CE=2(AE﹣CE)=2(),
当C△AEF﹣C△CEF=8时,有2()=8,(0<t<4),
解得t=3;
(3)四边形AEQF为菱形,则有S△EFG=S△AEF=S1,对角线AG与EF互相垂直平分,
S△GFC=S2=S△GFO﹣S△CFO=﹣,
∴S1﹣S2=S△AEF﹣S△GFC,
=S△AEF﹣(﹣)
=+
=6﹣4t﹣×(4﹣t)2]+
=8﹣2t,
当∠EAF=60°时,△AEF是等边三角形,
∴∠BAE=15°,
在AB边上取点H,使AH=HE,
则∠BHE=30°,
∴HE=2t,BH=,
∴2t+=4,
解得t=8﹣4.
∴S1﹣S2=8﹣2(8﹣4)=8﹣8.
同课章节目录
