湘教版八年级数学上册3.1.2算术平方根课件(共34张ppt)
文档属性
| 名称 | 湘教版八年级数学上册3.1.2算术平方根课件(共34张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-15 00:00:00 | ||
图片预览











文档简介
(共34张PPT)
第1节
平方根
第2课时
算术平方根
第3章
实数
逐点
导讲练
课堂小结
作业提升
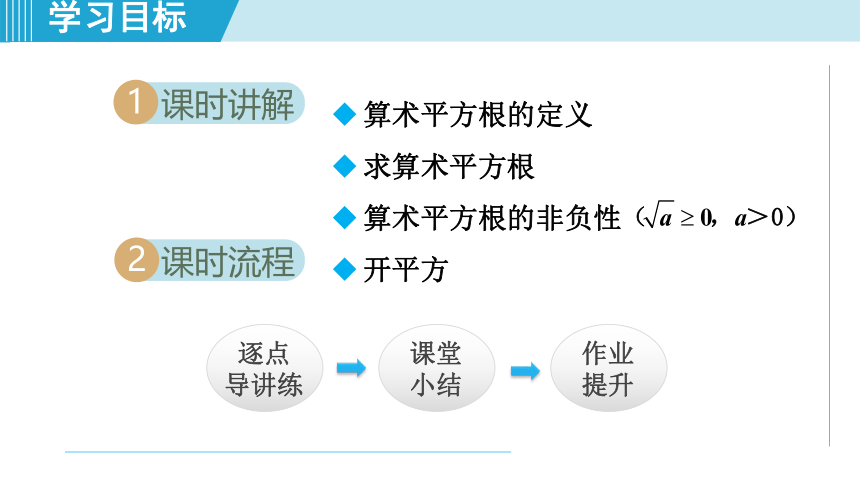
学习目标
课时讲解
1
课时流程
2
算术平方根的定义
求算术平方根
算术平方根的非负性
开平方
课时导入
复习提问
引出问题
复习提问
引出问题
如图所示,每个小正方形的边长是,我们通过剪开,拼接会得到大正方形,我知道小正方形的面积是1,因为右边的大正方形是由左边的两个小正
方形剪拼成的,所以大正方形的面
积是2.
课时导入
复习提问
引出问题
因为正方形的面积是边长乘一边长,所以a2=2,那么a等于多少呢?我们也就是找一个数,是它的平方等于2,由于正方形的边长是正数,所以就是找一个正数,使这个正数的平方等于2,我们把a叫做2的算术平方根,如果一个正数x的平方等于a,即x2=a,那么这个正数x就叫做a的算术平方根.
知识点
算术平方根的定义
知1-导
感悟新知
1
问题1:正数3的平方等于9,若x2=9,则正数x=____.正数4的平方等于16,若x2=16,则正数x=____.说说6和36这两个数又怎样的关系呢?
问题2:(1)0的平方是______,如果x2=0,那么x=______.
知1-导
感悟新知
问题3:学校要举行美术作品比赛,小鹏想裁出一块面积为
25
dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?你一定会算出边长应取5dm.说一说,你是怎样算出来的?
因为52=25,所以这个正方形画布的边长应取5
dm.
上面的问题,实际上是已知一个正数的平方,求这个正数的问题.
正方形的面积/dm2
1
9
16
36
正方形的边长/dm
知1-讲
结
论
感悟新知
一般地,如果r是正数a的一个平方根,那么a的平方根有且只有两个:r与-r.
我们把正数a的正平方根叫作a的算术平方根(arithmetic
square
root),记作
,读作“根号a”;把a的负平方根记作-
,读作“负根号a”.
知1-讲
感悟新知
1.定义:正数a的平方根叫作a的算术平方根.
规定:0的算术平方根是0.
表示方法:正数a的算术平方根表示为:
,读作“根号a”,a叫做被开方数.
知1-讲
感悟新知
特别提醒
●求一个正数的算术平
方根与求一个正数的
平方刚好是互逆的两
个运算
.
●任何一个数的平方都
是非负数,所以求算
术平方根时,根号内
的数必须是非负数,
它的算术平方根也一
定是非负数
.
知1-讲
感悟新知
例
1
导引:正确把握并准确运用平方根.算术平方根的定义.
下列说法中﹐正确的是(
)
A.9的平方根是±3,应表示为92=±3
B.
±3是9的平方根,应表示为±
=3
C.把9开平方能得到9的平方根,即
=±3
D.9的算术平方根是3,应表示为,
=3
D
知1-讲
总
结
感悟新知
算术平方根包含两层意思,这个数是非负数,它的算术平方根也是非负数.
知1-练
感悟新知
A
A
3.x是16的算术平方根,那么x的算术平方根是(
)
A.4
B.2
C.
D.±4
知1-练
感悟新知
B
知2-导
感悟新知
知识点
求算术平方根
2
当求得一个正数的算术平方根后,它的负的平方根可相应求得.
例如,9的算术平方根为3,它的负的平方根就是一3,
即
的算术平方根为
,它的负的平方根就是
,
即
0的平方根只有一个,就是0,我们也说0的算术平方根为0,
即
知2-导
感悟新知
问题:
求下列各数的算术平方根:
(1)144;
(2)0.01;
(3)
;
(4)132;
(5)(-16)2.
由平方根的意义,易知:当a>0时,
=a.
知2-讲
感悟新知
(1)正数的算术平方根是一个正数;
(2)0的算术平方根0;
(3)负数没有算术平方根:
(4)被开方数越大,对应的算术平方根也越大.
知2-讲
感悟新知
例2
分别求下列各数的算术平方根:100,
,0.49.
知2-讲
感悟新知
总
结
(1)求一个数的算术平方根时,首先要弄清是求哪个数的算术平方根,分清求
与81的算术平方根的不同意义,不要被表面现象迷惑求
的值实质是求81的算术平方根;求
的算术平方根实质是求9的算术平方根.
(2)求一个非负数的算术平方根常借助于平方运算,因此熟记常用平方数对求一个数的算术平方根十分有用.
1.如果一个正方形的面积是3,那么它的边长是________.
2.下列说法正确的是( )
A.9的算术平方根是±3
B.9的平方根是3
C.-9的平方根是-3
D.9的算术平方根是3
知2-练
感悟新知
D
知识点
算术平方根的非负性
知3-导
感悟新知
3
问题1.
(1)因为_____2=64,所以64的算术平方根是______,即
=______.
(2)因为_____2=0.25,所以0.25的算术平方根是______,即
=______.
(3)因为_____2=0,所以0的算术平方根是______,即
=______.
知3-导
感悟新知
问题2.讨论:在
中,被开方数a是一个____数,算术平方根
是一个_____数.
知3-讲
结
论
感悟新知
所以算术平方根
具有双重非负性:①被开方数a是____,即a≥0;②
算术平方根
本身是非负数,即____.
知3-讲
感悟新知
要点精析:
(1)算术平方根
具有双重非负性:
①被开方数a是非负数,即a
≥0;
②算术平方根
是非负数,即
≥0.
(2)算术平方根是它本身的数只有0和1.
知3-讲
感悟新知
例
3
已知y=
+
+5,求2x+y的算术平方根.
导引:由于只有非负数才有算术平方根,因此本题中x-2>0,且2-x=0,求得x的值后从而可得y的值,进而问题得解.
知3-讲
感悟新知
解:由
中a≥0知,等式成立的条件是:
x-2≥0且2-x≥0,所以x≥2且x≤2.
所以x=2,从而y=5.
所以2x+y=2×2+5=9.
因为9的算术平方根是3,
所以2x+y的算术平方根是3,即
=
=3.
知3-讲
总
结
感悟新知
被开方数具有非负性,即
中a≥0,当两个被开方数互为相反数时,只有它们都等于0,这两个式子才都有意义.
知3-练
感悟新知
B
知识点
开平方
知4-导
感悟新知
4
求一个非负数的平方根的运算,叫作开平方(extraction
of
square
root).
开平方与平方互为逆运算,根据这种关系,可以求一个数的平方根,
知4-讲
感悟新知
求下列各数的算术平方根:
导引:根据算术平方根的定义要求一个非负数的算术平方根,只要找到一个非负数的平方等于这个非负数即可.
例4
知4-讲
感悟新知
解:(1):82=64,∴64的算术平方根是8.
(2)∵
的算术平方根
(3)∵0.62=0.36,∴0.36的算术平方根是0.6.
术
知4-讲
总
结
感悟新知
正数a的算术平方根是一个正数,0的算术平方根是0,负数没有平方根.所以在计算时一定要注意,算术平方根只有一个而且是一个非负数.
知4-练
感悟新知
C
解析:因为16的算术平方根是4,4的算术平方根是2,所以选B.
B
课堂小结
算术平方根
通过这节课的学习,我们要掌握以下的内容:(1)算术平方根的概念,式子
中的双重非负性:一是a≥0,二是
≥0.(2)算术平方根的性质:一个正数的算术平方根是一个正数;0的算术平方根是0;负数没有算术平方根.(3)求一个正数的算术平方根的运算与平方运算是互逆的运算,利用这个互逆运算关系求非负数的算术平方根.
必做:
请完成教材课后习题
课后作业
作业
第1节
平方根
第2课时
算术平方根
第3章
实数
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
算术平方根的定义
求算术平方根
算术平方根的非负性
开平方
课时导入
复习提问
引出问题
复习提问
引出问题
如图所示,每个小正方形的边长是,我们通过剪开,拼接会得到大正方形,我知道小正方形的面积是1,因为右边的大正方形是由左边的两个小正
方形剪拼成的,所以大正方形的面
积是2.
课时导入
复习提问
引出问题
因为正方形的面积是边长乘一边长,所以a2=2,那么a等于多少呢?我们也就是找一个数,是它的平方等于2,由于正方形的边长是正数,所以就是找一个正数,使这个正数的平方等于2,我们把a叫做2的算术平方根,如果一个正数x的平方等于a,即x2=a,那么这个正数x就叫做a的算术平方根.
知识点
算术平方根的定义
知1-导
感悟新知
1
问题1:正数3的平方等于9,若x2=9,则正数x=____.正数4的平方等于16,若x2=16,则正数x=____.说说6和36这两个数又怎样的关系呢?
问题2:(1)0的平方是______,如果x2=0,那么x=______.
知1-导
感悟新知
问题3:学校要举行美术作品比赛,小鹏想裁出一块面积为
25
dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?你一定会算出边长应取5dm.说一说,你是怎样算出来的?
因为52=25,所以这个正方形画布的边长应取5
dm.
上面的问题,实际上是已知一个正数的平方,求这个正数的问题.
正方形的面积/dm2
1
9
16
36
正方形的边长/dm
知1-讲
结
论
感悟新知
一般地,如果r是正数a的一个平方根,那么a的平方根有且只有两个:r与-r.
我们把正数a的正平方根叫作a的算术平方根(arithmetic
square
root),记作
,读作“根号a”;把a的负平方根记作-
,读作“负根号a”.
知1-讲
感悟新知
1.定义:正数a的平方根叫作a的算术平方根.
规定:0的算术平方根是0.
表示方法:正数a的算术平方根表示为:
,读作“根号a”,a叫做被开方数.
知1-讲
感悟新知
特别提醒
●求一个正数的算术平
方根与求一个正数的
平方刚好是互逆的两
个运算
.
●任何一个数的平方都
是非负数,所以求算
术平方根时,根号内
的数必须是非负数,
它的算术平方根也一
定是非负数
.
知1-讲
感悟新知
例
1
导引:正确把握并准确运用平方根.算术平方根的定义.
下列说法中﹐正确的是(
)
A.9的平方根是±3,应表示为92=±3
B.
±3是9的平方根,应表示为±
=3
C.把9开平方能得到9的平方根,即
=±3
D.9的算术平方根是3,应表示为,
=3
D
知1-讲
总
结
感悟新知
算术平方根包含两层意思,这个数是非负数,它的算术平方根也是非负数.
知1-练
感悟新知
A
A
3.x是16的算术平方根,那么x的算术平方根是(
)
A.4
B.2
C.
D.±4
知1-练
感悟新知
B
知2-导
感悟新知
知识点
求算术平方根
2
当求得一个正数的算术平方根后,它的负的平方根可相应求得.
例如,9的算术平方根为3,它的负的平方根就是一3,
即
的算术平方根为
,它的负的平方根就是
,
即
0的平方根只有一个,就是0,我们也说0的算术平方根为0,
即
知2-导
感悟新知
问题:
求下列各数的算术平方根:
(1)144;
(2)0.01;
(3)
;
(4)132;
(5)(-16)2.
由平方根的意义,易知:当a>0时,
=a.
知2-讲
感悟新知
(1)正数的算术平方根是一个正数;
(2)0的算术平方根0;
(3)负数没有算术平方根:
(4)被开方数越大,对应的算术平方根也越大.
知2-讲
感悟新知
例2
分别求下列各数的算术平方根:100,
,0.49.
知2-讲
感悟新知
总
结
(1)求一个数的算术平方根时,首先要弄清是求哪个数的算术平方根,分清求
与81的算术平方根的不同意义,不要被表面现象迷惑求
的值实质是求81的算术平方根;求
的算术平方根实质是求9的算术平方根.
(2)求一个非负数的算术平方根常借助于平方运算,因此熟记常用平方数对求一个数的算术平方根十分有用.
1.如果一个正方形的面积是3,那么它的边长是________.
2.下列说法正确的是( )
A.9的算术平方根是±3
B.9的平方根是3
C.-9的平方根是-3
D.9的算术平方根是3
知2-练
感悟新知
D
知识点
算术平方根的非负性
知3-导
感悟新知
3
问题1.
(1)因为_____2=64,所以64的算术平方根是______,即
=______.
(2)因为_____2=0.25,所以0.25的算术平方根是______,即
=______.
(3)因为_____2=0,所以0的算术平方根是______,即
=______.
知3-导
感悟新知
问题2.讨论:在
中,被开方数a是一个____数,算术平方根
是一个_____数.
知3-讲
结
论
感悟新知
所以算术平方根
具有双重非负性:①被开方数a是____,即a≥0;②
算术平方根
本身是非负数,即____.
知3-讲
感悟新知
要点精析:
(1)算术平方根
具有双重非负性:
①被开方数a是非负数,即a
≥0;
②算术平方根
是非负数,即
≥0.
(2)算术平方根是它本身的数只有0和1.
知3-讲
感悟新知
例
3
已知y=
+
+5,求2x+y的算术平方根.
导引:由于只有非负数才有算术平方根,因此本题中x-2>0,且2-x=0,求得x的值后从而可得y的值,进而问题得解.
知3-讲
感悟新知
解:由
中a≥0知,等式成立的条件是:
x-2≥0且2-x≥0,所以x≥2且x≤2.
所以x=2,从而y=5.
所以2x+y=2×2+5=9.
因为9的算术平方根是3,
所以2x+y的算术平方根是3,即
=
=3.
知3-讲
总
结
感悟新知
被开方数具有非负性,即
中a≥0,当两个被开方数互为相反数时,只有它们都等于0,这两个式子才都有意义.
知3-练
感悟新知
B
知识点
开平方
知4-导
感悟新知
4
求一个非负数的平方根的运算,叫作开平方(extraction
of
square
root).
开平方与平方互为逆运算,根据这种关系,可以求一个数的平方根,
知4-讲
感悟新知
求下列各数的算术平方根:
导引:根据算术平方根的定义要求一个非负数的算术平方根,只要找到一个非负数的平方等于这个非负数即可.
例4
知4-讲
感悟新知
解:(1):82=64,∴64的算术平方根是8.
(2)∵
的算术平方根
(3)∵0.62=0.36,∴0.36的算术平方根是0.6.
术
知4-讲
总
结
感悟新知
正数a的算术平方根是一个正数,0的算术平方根是0,负数没有平方根.所以在计算时一定要注意,算术平方根只有一个而且是一个非负数.
知4-练
感悟新知
C
解析:因为16的算术平方根是4,4的算术平方根是2,所以选B.
B
课堂小结
算术平方根
通过这节课的学习,我们要掌握以下的内容:(1)算术平方根的概念,式子
中的双重非负性:一是a≥0,二是
≥0.(2)算术平方根的性质:一个正数的算术平方根是一个正数;0的算术平方根是0;负数没有算术平方根.(3)求一个正数的算术平方根的运算与平方运算是互逆的运算,利用这个互逆运算关系求非负数的算术平方根.
必做:
请完成教材课后习题
课后作业
作业
同课章节目录
