湘教版八年级数学上册3.1.3无理数及其求法课件(共29张ppt)
文档属性
| 名称 | 湘教版八年级数学上册3.1.3无理数及其求法课件(共29张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-15 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
第1节
平方根
第3课时
无理数及其求法
第3章
实数
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
有理数及其局限性
估算
用计算器求一个正数的算术平方根
课时导入
复习提问
引出问题
复习提问
引出问题
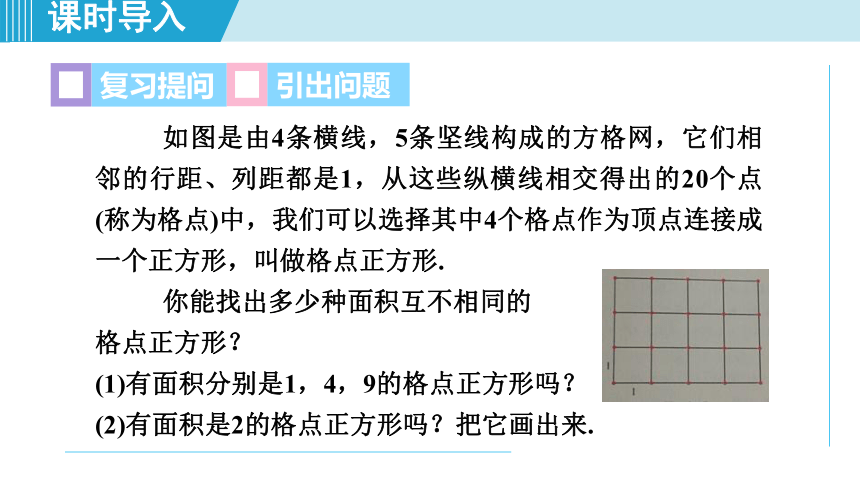
如图是由4条横线,5条坚线构成的方格网,它们相邻的行距、列距都是1,从这些纵横线相交得出的20个点(称为格点)中,我们可以选择其中4个格点作为顶点连接成一个正方形,叫做格点正方形.
你能找出多少种面积互不相同的
格点正方形?
(1)有面积分别是1,4,9的格点正方形吗?
(2)有面积是2的格点正方形吗?把它画出来.
知识点
有理数及其局限性
知1-导
感悟新知
1
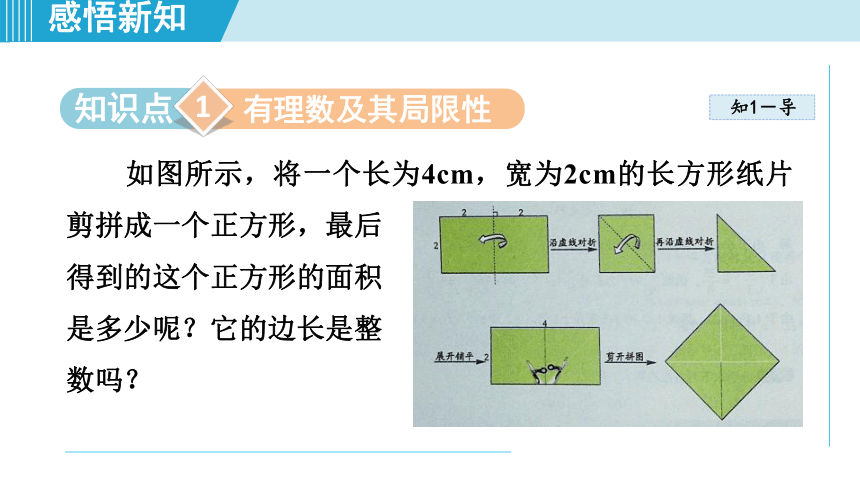
如图所示,将一个长为4cm,宽为2cm的长方形纸片剪拼成一个正方形,最后
得到的这个正方形的面积
是多少呢?它的边长是整
数吗?
知1-导
感悟新知
正方形的面积为8cm2,由于22=4,32=9,又4<8<9,且面积较大的正方形的边长也较大,因此面积为8cm2的正方形的边长不是整数.
知1-导
感悟新知
问题1:观察下列结果:
2.82=7.84,
2.92=
8.41;
2.82=
7.9524,
2.832=8.0089;
2.8282=
7.997
584,
2.8292=8.003
241;
…
…
从上述数据,你能猜出面积为8的正方形的边长是多少吗?
知1-导
感悟新知
面积为8的正方形,它的边长应该比2.828大,比2.829小,....
由此猜想,面积为8cm2的正方形,它的边长是一个小数点后面的位数可以不断增加的小数.
知1-导
感悟新知
问题2:有理数包括整数和分数两部分.
(1)整数可以写成小数的形式,如
-10=-10.0,-1=-1.0,0=0.0,50
=50.0.
对于任意给定的一个整数,你能将它写成小数的形式吗?
(2)分数可以写成有限小数或无限循环小数,如
知1-导
感悟新知
任意给定一个分数,你能将它写成有限小数或无限循环小数的形式吗?(可以借助计算器计算)
(3)有理数是不是总可以写成有限小数或无限循环小数的形式呢?
事实上,有理数总可以写成有限小数或无限循环小数的形式,而
,π是无限不循环小数.
知1-讲
结
论
感悟新知
事实上,我们可以说明这个边长不是分数,从而它既不是有限小数,也不是无限循环小数,这种小数叫作无限不循环小数,我们把无限不循环小数叫作无理数(irrational
number).
知1-讲
感悟新知
1.根据实际需要,我们往往用一个有限小数来近似地表示一个无理数.例如π=3.141
592
65…,四舍五入法,分别取到小数点后面第二位,第三位,…得到π≈3.14,
π≈
3.142,…,我们称3.14,3.142是π精确到小数点后面第二位,第三位的近似值.
3.14,3.142,3.141
6,…都是π的近似值,称它们为近似数.
知1-讲
感悟新知
2.无理数常见的有如下几种类型:①含π型:如π
-3.41,2π,
,…
②根号型:一些带根号且开不尽方的数,如
但要注意并非所有带根号的数都是无理数;③构造型:如0.101
001
000
1..,1.121
122
112
221
1..,这样一些有一定规律但无限不循环的数;④其他形式的无理数.
知1-讲
感悟新知
3.无理数与有理数的区别:
(1)有理数是有限小数和无限循环小数,而无理是无限不循环小数;
(2)所有的有理数都可以写成分数的形式(整数可以看成分母为1的分数),而无理数不能写成分数的形式.
4.易错警示:(1)带根号的数不一定是无理数,不带根号的数也不一定是有理数;
(2)无理数都是无限小数,但无限小数不一定是无理数.
知1-讲
感悟新知
例
1
下列各数:3.141
59,
,0.131
131
113…(每相邻两个3之间依次多1个1),-π,
,
中,无理数有(
)
A.1个
B.2个
C.3个
D.4个
B
知1-讲
感悟新知
导引:3.141
59是有限小数,∴3.141
59是有理数.
∵
=-2,∴
是有理数.
∵
=5,∴
是有理数.
∵
是分数.
∴
是有理数
∵
0.131
131
113(每相邻两个3之间依次多1个1),-π都是无限不循环小数,
∴0.131
131
113…(每相邻两个3之间依次多1个1),-π是无理数,故选B.
知1-讲
总
结
感悟新知
(1)对有理数和无理数进行区分时,应先对某些数进行计算或化简,然后根据最后结果进行分类,不能仅看到用根号表示的数就认为是无理数.
(2)π是无理数,化简后含π的数也是无理数.
1.下列说法正确的是( )
A.0.101
001
000
1是无理数
B.无限小数不能转化成分数
C.无理数分为正无理数、零、负无理数
D.无限不循环小数是无理数
知1-练
感悟新知
D
知1-练
感悟新知
C
2.下列关于0的说法正确的是( )
A.0是正数
B.0是负数
C.0是有理数
D.0是无理数
知2-导
感悟新知
知识点
估算
2
由于正方形的边长的平方等于它的面积,因此面积为8cm2的正方形的边长可以记作
cm.从上述分析知道,
是一个无限不循环小数,即
是一个无理数.
圆周率π=3.141
592
6
…
,也是一个无理数.
=1.414
2136
…
,
=1.732
050
8
…
,…都是无理数.
与有理数一样,无理数也有正负之分,例如,
,
,π是正无理数,-
,-
,-π是负无理数.
知2-导
感悟新知
根据实际需要,我们往往用一个有限小数来近似地表示一个无理数.
例如
π=3.141
592
65…,用四舍五人法,分别取到小数点后面第二位,第三位,…,得到π≈3.14,π≈3.142,…,我们称3.14,3.142是π的精确到小数点后面第二位,第三位的近似值.
314,3.142,3.1416,…都是π的近似值,称它们为近似数
知2-讲
感悟新知
例2
估计
的大小应在(
)
A.7
~8
B.8.0
~8.5
C.8.5
~9.0
D.9.0
~10
C
分析:因为82=64,92=81,所以排除选项A,D,又因为8.52=72.25,所以8.5<
<9.0.
点拨:估算一个数的平方根的大致范围常借助平方运算.
知2-练
感悟新知
D
2.12的平方根介于(
)
A.4与5之间
B.
3与4之间
C.
2与3之间
D.
1与2之间
知2-练
感悟新知
B
解析:根据实数估计大小,
12介于32和42之间,所以12的平方根
介于3与4之间.
知识点
用计算器求一个正数的算术平方根
知3-导
感悟新知
3
利用计算器可以求一个正数的算术平方根或它的近似值.
知3-讲
感悟新知
例
3
用计算器求下列各式的值.
(1)
;
(2)
(精确到小数点后面第三位).
知3-讲
感悟新知
解:(1)依次按键:
显示:32
所以,
=32.
(2)依次按键:
显示:2.828
427
125
所以,
≈2.828.
知3-练
感悟新知
C
课堂小结
无理数及其求法
有理数和无理数的区别
1.小数区别:有理数包括有限小数和无限循环小数,而无理数是无限不循环小数.
2.根据区别:有理数能化为分数,而无理数不能化为分数.
必做:
请完成教材课后习题
课后作业
作业
第1节
平方根
第3课时
无理数及其求法
第3章
实数
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
有理数及其局限性
估算
用计算器求一个正数的算术平方根
课时导入
复习提问
引出问题
复习提问
引出问题
如图是由4条横线,5条坚线构成的方格网,它们相邻的行距、列距都是1,从这些纵横线相交得出的20个点(称为格点)中,我们可以选择其中4个格点作为顶点连接成一个正方形,叫做格点正方形.
你能找出多少种面积互不相同的
格点正方形?
(1)有面积分别是1,4,9的格点正方形吗?
(2)有面积是2的格点正方形吗?把它画出来.
知识点
有理数及其局限性
知1-导
感悟新知
1
如图所示,将一个长为4cm,宽为2cm的长方形纸片剪拼成一个正方形,最后
得到的这个正方形的面积
是多少呢?它的边长是整
数吗?
知1-导
感悟新知
正方形的面积为8cm2,由于22=4,32=9,又4<8<9,且面积较大的正方形的边长也较大,因此面积为8cm2的正方形的边长不是整数.
知1-导
感悟新知
问题1:观察下列结果:
2.82=7.84,
2.92=
8.41;
2.82=
7.9524,
2.832=8.0089;
2.8282=
7.997
584,
2.8292=8.003
241;
…
…
从上述数据,你能猜出面积为8的正方形的边长是多少吗?
知1-导
感悟新知
面积为8的正方形,它的边长应该比2.828大,比2.829小,....
由此猜想,面积为8cm2的正方形,它的边长是一个小数点后面的位数可以不断增加的小数.
知1-导
感悟新知
问题2:有理数包括整数和分数两部分.
(1)整数可以写成小数的形式,如
-10=-10.0,-1=-1.0,0=0.0,50
=50.0.
对于任意给定的一个整数,你能将它写成小数的形式吗?
(2)分数可以写成有限小数或无限循环小数,如
知1-导
感悟新知
任意给定一个分数,你能将它写成有限小数或无限循环小数的形式吗?(可以借助计算器计算)
(3)有理数是不是总可以写成有限小数或无限循环小数的形式呢?
事实上,有理数总可以写成有限小数或无限循环小数的形式,而
,π是无限不循环小数.
知1-讲
结
论
感悟新知
事实上,我们可以说明这个边长不是分数,从而它既不是有限小数,也不是无限循环小数,这种小数叫作无限不循环小数,我们把无限不循环小数叫作无理数(irrational
number).
知1-讲
感悟新知
1.根据实际需要,我们往往用一个有限小数来近似地表示一个无理数.例如π=3.141
592
65…,四舍五入法,分别取到小数点后面第二位,第三位,…得到π≈3.14,
π≈
3.142,…,我们称3.14,3.142是π精确到小数点后面第二位,第三位的近似值.
3.14,3.142,3.141
6,…都是π的近似值,称它们为近似数.
知1-讲
感悟新知
2.无理数常见的有如下几种类型:①含π型:如π
-3.41,2π,
,…
②根号型:一些带根号且开不尽方的数,如
但要注意并非所有带根号的数都是无理数;③构造型:如0.101
001
000
1..,1.121
122
112
221
1..,这样一些有一定规律但无限不循环的数;④其他形式的无理数.
知1-讲
感悟新知
3.无理数与有理数的区别:
(1)有理数是有限小数和无限循环小数,而无理是无限不循环小数;
(2)所有的有理数都可以写成分数的形式(整数可以看成分母为1的分数),而无理数不能写成分数的形式.
4.易错警示:(1)带根号的数不一定是无理数,不带根号的数也不一定是有理数;
(2)无理数都是无限小数,但无限小数不一定是无理数.
知1-讲
感悟新知
例
1
下列各数:3.141
59,
,0.131
131
113…(每相邻两个3之间依次多1个1),-π,
,
中,无理数有(
)
A.1个
B.2个
C.3个
D.4个
B
知1-讲
感悟新知
导引:3.141
59是有限小数,∴3.141
59是有理数.
∵
=-2,∴
是有理数.
∵
=5,∴
是有理数.
∵
是分数.
∴
是有理数
∵
0.131
131
113(每相邻两个3之间依次多1个1),-π都是无限不循环小数,
∴0.131
131
113…(每相邻两个3之间依次多1个1),-π是无理数,故选B.
知1-讲
总
结
感悟新知
(1)对有理数和无理数进行区分时,应先对某些数进行计算或化简,然后根据最后结果进行分类,不能仅看到用根号表示的数就认为是无理数.
(2)π是无理数,化简后含π的数也是无理数.
1.下列说法正确的是( )
A.0.101
001
000
1是无理数
B.无限小数不能转化成分数
C.无理数分为正无理数、零、负无理数
D.无限不循环小数是无理数
知1-练
感悟新知
D
知1-练
感悟新知
C
2.下列关于0的说法正确的是( )
A.0是正数
B.0是负数
C.0是有理数
D.0是无理数
知2-导
感悟新知
知识点
估算
2
由于正方形的边长的平方等于它的面积,因此面积为8cm2的正方形的边长可以记作
cm.从上述分析知道,
是一个无限不循环小数,即
是一个无理数.
圆周率π=3.141
592
6
…
,也是一个无理数.
=1.414
2136
…
,
=1.732
050
8
…
,…都是无理数.
与有理数一样,无理数也有正负之分,例如,
,
,π是正无理数,-
,-
,-π是负无理数.
知2-导
感悟新知
根据实际需要,我们往往用一个有限小数来近似地表示一个无理数.
例如
π=3.141
592
65…,用四舍五人法,分别取到小数点后面第二位,第三位,…,得到π≈3.14,π≈3.142,…,我们称3.14,3.142是π的精确到小数点后面第二位,第三位的近似值.
314,3.142,3.1416,…都是π的近似值,称它们为近似数
知2-讲
感悟新知
例2
估计
的大小应在(
)
A.7
~8
B.8.0
~8.5
C.8.5
~9.0
D.9.0
~10
C
分析:因为82=64,92=81,所以排除选项A,D,又因为8.52=72.25,所以8.5<
<9.0.
点拨:估算一个数的平方根的大致范围常借助平方运算.
知2-练
感悟新知
D
2.12的平方根介于(
)
A.4与5之间
B.
3与4之间
C.
2与3之间
D.
1与2之间
知2-练
感悟新知
B
解析:根据实数估计大小,
12介于32和42之间,所以12的平方根
介于3与4之间.
知识点
用计算器求一个正数的算术平方根
知3-导
感悟新知
3
利用计算器可以求一个正数的算术平方根或它的近似值.
知3-讲
感悟新知
例
3
用计算器求下列各式的值.
(1)
;
(2)
(精确到小数点后面第三位).
知3-讲
感悟新知
解:(1)依次按键:
显示:32
所以,
=32.
(2)依次按键:
显示:2.828
427
125
所以,
≈2.828.
知3-练
感悟新知
C
课堂小结
无理数及其求法
有理数和无理数的区别
1.小数区别:有理数包括有限小数和无限循环小数,而无理数是无限不循环小数.
2.根据区别:有理数能化为分数,而无理数不能化为分数.
必做:
请完成教材课后习题
课后作业
作业
同课章节目录
