湘教版八年级数学上册3.3实数课件(共42张ppt)
文档属性
| 名称 | 湘教版八年级数学上册3.3实数课件(共42张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-15 00:00:00 | ||
图片预览










文档简介
(共42张PPT)
第3节
实数
第3章
实数
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
实数及其分类
实数的性质
实数与数轴的关系
实数的大小比较
实数的运算
课时导入
复习提问
引出问题
复习提问
引出问题
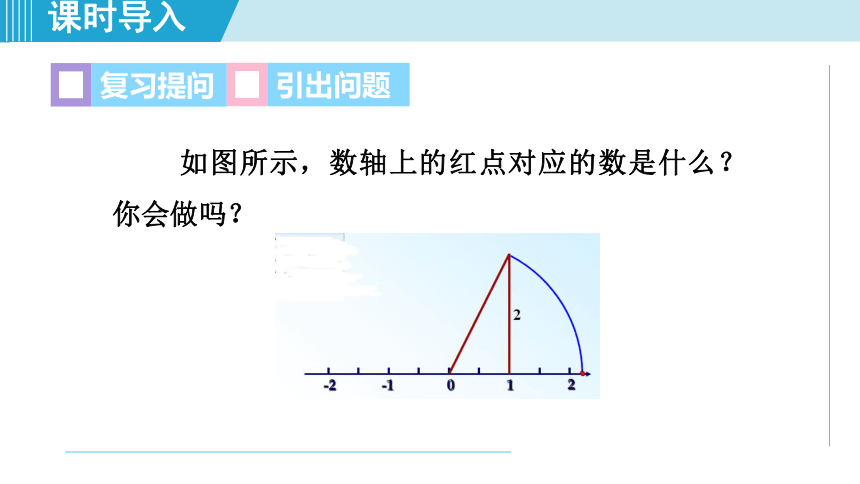
如图所示,数轴上的红点对应的数是什么?
你会做吗?
知识点
实数及其分类
知1-导
感悟新知
1
下列各数中,哪些是有理数?哪些是无理数?
,0,144,
,π,
,
,0.101
001
0001…(邻两个1之间逐次增加一个0).
解:0,1.414,
,
是有理数,
,π,
,0.1010
000
1是无理数.
知1-讲
结
论
感悟新知
有理数和无理数统称为实数(real
number).这样,我们可以得到:
知1-讲
感悟新知
例
1
导引:以前学过的0以外的数就是正数,正数前面加上“-”号就是负数,再看它们是整数还是分数.
把下列各数分别填在相应的括号内.
,13,-12,+6,
,0,0.8,
,-4.2.
正数:{
,…};负数:{
,…};
正整数:{
,…};正分数:{
,…};负整数:{
,…};负分数:{
,…}.
知1-讲
感悟新知
点拨:从两个方面看,一是判断正负情况,二是判断是整数还是分数.有限小数和无限循环小数都属于分数.
知1-讲
感悟新知
解:正数:{
…};
负数:{
…};
正整数:{
…};
正分数:{
…};
负整数:
{
…};
负分数:{
…}.
知1-练
感悟新知
D
1.下列说法正确的是( )
A.正实数和负实数统称实数
B.正数、零和负数统称有理数
C.带根号的数和分数统称实数
D.无理数和有理数统称实数
知2-导
感悟新知
知识点
实数的性质
2
参照有理数的有关概念,谈谈实数的下列概念:
(1)实数的绝对值.
(2)互为相反数的实数.
(3)一个实数的倒数.
知2-导
感悟新知
结
论
在数轴上,实数的绝对值意义也与有理数一样;正实数的绝对值是它本身,负实数的绝对值是它的相反数,0的绝对值是0.例如:
设a表示一个实数,则
a,当a>0时,
∣a
∣=
a,当a=0时,
a,当a<0时,
知2-讲
感悟新知
1.在有理数范围内的一些基本概念(如相反数、倒数、绝对值)在实数范围内依然适用.
(1)相反数:实数a的相反数为-a,若a,b互为相反数,则a+b=0;
(2)非零实数a的倒数为
,若a,b互为倒数,则ab=1;
(3)绝对值:∣a
∣=
a(a≥0)
-a(a<0).
知2-讲
感悟新知
例2
求下列各数的相反数和绝对值:
,π-3.14.
解:因为
,-(π-3.14)=3.14-π,
所以,
,π-3.14的相反数分别为
,3.14-π.
由绝对值的意义得:
∣π-3.14∣=π-3.14.
知2-讲
感悟新知
总
结
实数的性质与有理数的性质一样.
知识点
实数与数轴的关系
知3-导
感悟新知
3
如何用数轴上的点表示无理数
和-
?
我们已经知道,一个面积为8的正方形(如图3-3)的边长是
.因此我们以数轴的原点O为圆心,以正方形的边长为半径画孤,与正半轴的交点M就表示
,与负半轴的交点N就表示-
,如图3-4所示,这样,我们就分别用数轴上唯一的一个点表示出了无理数
和-
.
事实上,每一个无理数
都可以用数轴上唯一的一个
点来表示.
知3-讲
结
论
感悟新知
因此综上所还可知:
每一个实数都可以用数轴上唯一的一个点来表示.
反过来,还可以说明:
数轴上每一个点都表示唯一的一个实数.
上面两个结论合起来可以简洁地说成:
实数和数轴上的点一一对应.
知3-讲
感悟新知
1.实数与数轴间的关系:实数和数轴上的点对应,它包含着两层含义:(1)每一个实数都可以用数轴上的一个点来表示;(2)数轴上的每一个点都表示一个实数.
知3-讲
感悟新知
例
3
用“<”连接下列各数:
导引:比较一组实数的大小和比较一组有理数的大小一样,可先求出这些数的近似数,再将这些数在数轴上表示出来,然后根据“在数轴上右边的点表示的数总比左边的点表示的数大”求解.
知3-讲
感悟新知
解:将各数的大致位置在数轴上表示出来,如图.
由图可知,用“<”
可以连接成:
知3-讲
结
论
感悟新知
根据“实数与数轴上的点是一一对应的关系”,并且“在数轴上右边的点表示的数总比左边的点表示的数大”,我们可以利用数形结合思想比较实数的大小.
知3-练
感悟新知
C
知识点
实数的大小比较
知4-导
感悟新知
4
利用数轴,我们可以比较两个有理数的大小.因为在数轴上表示的数,右边的数总比左边的数大.因为在数轴上3在2的右边,所以3>2,-2在-3的右边,所以-2___-3;
因为在数轴上
在
的右边,所以
__
,
-
在-
的右边,所以-
____-
,同理:0____
-
;
-
____-
.
知4-讲
结
论
感悟新知
在实数范围内,在数轴上表示的数,右边的数总比左边的数大.
知4-讲
感悟新知
正实数大于0,负实数小于0;正实数大于一切负实数;两个负实数比较大小,绝对值大的反而小.
知4-讲
感悟新知
比较下列各组数中两个数的大小:
例2
解:(1)因为
知4-讲
感悟新知
(2)因为
=10,π2=(3.141
5…)2,而10>3.152>π2,所以
>π.从而-
<-π.
知4-讲
总
结
感悟新知
当题目中直接比较大小较困难时,我们可以采用特殊值法,所取特殊值必须符合两个条件:
(1)在字母取值范围内;(2)求值计算简单,而求实数的相反数、倒数、绝对值的方法与求有理数的相反数、倒数、绝对值的方法是一样的.
知识点
实数的运算
知5-导
感悟新知
5
填空:设a,b,c是任意实数,则
(1)a+b=___________(加法交换律);
(2)(a+b)+c=___________(加法结合律);
(3)a+0=0+a
=___________;
(4)a+(-a)=(-a)+a=___________;
(5)ab=___________(乘法交换律);
(6)(ab)c=________(乘法结合律);
(7)1·a=a·1=________;
(8)a(b
+c)=________(乘法对于加法的分配律),
(b+c)a=________(乘法对于加法的分配律);
(9)实数的减法运算规定为a-b=a+____;
(10)对于每一个非零实数a,存在一个实数b,满足a·b=b·a=1,我们把b叫作a的________;
(11)实数的除法运算(除数b≠0),规定为a÷b=a·________;
(12)实数有一条重要性质:如果a≠0,b≠0,那么ab________0.
知5-导
感悟新知
知5-讲
感悟新知
1.在实数范围内,进行加、减、乘、除、乘方和开方运算时,有理数的运算法则和运算律仍然适用;实数混合运算的运算顺序与有理数的混合运算顺序一样,先算乘方、开方,再算乘除,最后算加减,同级运算按照自左向右的顺序进行,有括号先算括号里面的。
知5-讲
感悟新知
2.有理数的运算律在实数范围内仍然适用,在进行实数运算的过程中,要做到:一“看”——看算式的结构特点,能否运用运算律或公式;二“用”——运用运算律或公式;三“查”——检查过程和结果是否正确.
知5-讲
感悟新知
3.学法指南:实数的运算律
加法交换律:a+b=b+a;
加法结合律:(a+b)+c=a+(b+c);
乘法交换律:ab=ba;
乘法结合律:(ab)c
=a(bc);
乘法分配律:(a+b)c=ac
+bc.
知5-讲
感悟新知
要点精析:在实数范围内做开方运算时,要注意正实数和零既能开平方,也能开立方,负实数不能开平方.
(1)运算种类:
运算级别
第一级
第二级
第三级
运算名称
加
减
乘
除
乘方
平方
运算结果
和
差
积
商
幂
方根
知5-讲
感悟新知
(2)运算顺序:先乘方、开方,再乘除,最后算加减同级运算按照从左到右的顺序进行,有括号的先算括号里面的.
(3)运算律:与有理数运算律一致.
4.易错警示:(1)负实数只能开奇次方,不能开偶次方;
(2)计算结果中如果包含开方开不尽的数,则保留根号,结果要化为最简形式.
知5-讲
感悟新知
计算下列各式的值:
(加法结合律)
例
5
知5-讲
感悟新知
(乘法对于加法的分配律)
知5-讲
总
结
感悟新知
实数的运算同有理数的运算.实数运算中,无理数可选取近似值转化为有理数计算,中间结果所取的近似值要比结果要求多一位小数.
课堂小结
1.当数的范国从有理数扩充到实数后,有理教中关于相反数、例数和绝对值的相关性质同样适用于实数.
2.实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上一个点来表示,反过来敦轴上的任何一个点都表示一个实数.
实数
课堂小结
2.实数运算时要先确定运算符号及顺序,再进行运算,运算过程中要热练运用运算律及各种运算法则,掌握一定的运算技巧,同时要明确除开偶次方外,其他各种运算在实数范围内都能实施,且运算结果是唯一的;开偶次方只有在非负实数范围内才能实施,且正数的偶次方根有两个.
实数
课堂小结
运算种类:
运算级别
第一级
第二级
第三级
运算名称
加
减
乘
除
乘方
平方
运算结果
和
差
积
商
幂
方根
实数
课堂小结
3.易错警示:(1)负实数只能开奇次方,不能开偶次方;
(2)计算结果中如果包含开方开不尽的数,则保留根号,结果要化为最简形式.
实数
必做:
请完成教材课后习题
课后作业
作业
第3节
实数
第3章
实数
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
实数及其分类
实数的性质
实数与数轴的关系
实数的大小比较
实数的运算
课时导入
复习提问
引出问题
复习提问
引出问题
如图所示,数轴上的红点对应的数是什么?
你会做吗?
知识点
实数及其分类
知1-导
感悟新知
1
下列各数中,哪些是有理数?哪些是无理数?
,0,144,
,π,
,
,0.101
001
0001…(邻两个1之间逐次增加一个0).
解:0,1.414,
,
是有理数,
,π,
,0.1010
000
1是无理数.
知1-讲
结
论
感悟新知
有理数和无理数统称为实数(real
number).这样,我们可以得到:
知1-讲
感悟新知
例
1
导引:以前学过的0以外的数就是正数,正数前面加上“-”号就是负数,再看它们是整数还是分数.
把下列各数分别填在相应的括号内.
,13,-12,+6,
,0,0.8,
,-4.2.
正数:{
,…};负数:{
,…};
正整数:{
,…};正分数:{
,…};负整数:{
,…};负分数:{
,…}.
知1-讲
感悟新知
点拨:从两个方面看,一是判断正负情况,二是判断是整数还是分数.有限小数和无限循环小数都属于分数.
知1-讲
感悟新知
解:正数:{
…};
负数:{
…};
正整数:{
…};
正分数:{
…};
负整数:
{
…};
负分数:{
…}.
知1-练
感悟新知
D
1.下列说法正确的是( )
A.正实数和负实数统称实数
B.正数、零和负数统称有理数
C.带根号的数和分数统称实数
D.无理数和有理数统称实数
知2-导
感悟新知
知识点
实数的性质
2
参照有理数的有关概念,谈谈实数的下列概念:
(1)实数的绝对值.
(2)互为相反数的实数.
(3)一个实数的倒数.
知2-导
感悟新知
结
论
在数轴上,实数的绝对值意义也与有理数一样;正实数的绝对值是它本身,负实数的绝对值是它的相反数,0的绝对值是0.例如:
设a表示一个实数,则
a,当a>0时,
∣a
∣=
a,当a=0时,
a,当a<0时,
知2-讲
感悟新知
1.在有理数范围内的一些基本概念(如相反数、倒数、绝对值)在实数范围内依然适用.
(1)相反数:实数a的相反数为-a,若a,b互为相反数,则a+b=0;
(2)非零实数a的倒数为
,若a,b互为倒数,则ab=1;
(3)绝对值:∣a
∣=
a(a≥0)
-a(a<0).
知2-讲
感悟新知
例2
求下列各数的相反数和绝对值:
,π-3.14.
解:因为
,-(π-3.14)=3.14-π,
所以,
,π-3.14的相反数分别为
,3.14-π.
由绝对值的意义得:
∣π-3.14∣=π-3.14.
知2-讲
感悟新知
总
结
实数的性质与有理数的性质一样.
知识点
实数与数轴的关系
知3-导
感悟新知
3
如何用数轴上的点表示无理数
和-
?
我们已经知道,一个面积为8的正方形(如图3-3)的边长是
.因此我们以数轴的原点O为圆心,以正方形的边长为半径画孤,与正半轴的交点M就表示
,与负半轴的交点N就表示-
,如图3-4所示,这样,我们就分别用数轴上唯一的一个点表示出了无理数
和-
.
事实上,每一个无理数
都可以用数轴上唯一的一个
点来表示.
知3-讲
结
论
感悟新知
因此综上所还可知:
每一个实数都可以用数轴上唯一的一个点来表示.
反过来,还可以说明:
数轴上每一个点都表示唯一的一个实数.
上面两个结论合起来可以简洁地说成:
实数和数轴上的点一一对应.
知3-讲
感悟新知
1.实数与数轴间的关系:实数和数轴上的点对应,它包含着两层含义:(1)每一个实数都可以用数轴上的一个点来表示;(2)数轴上的每一个点都表示一个实数.
知3-讲
感悟新知
例
3
用“<”连接下列各数:
导引:比较一组实数的大小和比较一组有理数的大小一样,可先求出这些数的近似数,再将这些数在数轴上表示出来,然后根据“在数轴上右边的点表示的数总比左边的点表示的数大”求解.
知3-讲
感悟新知
解:将各数的大致位置在数轴上表示出来,如图.
由图可知,用“<”
可以连接成:
知3-讲
结
论
感悟新知
根据“实数与数轴上的点是一一对应的关系”,并且“在数轴上右边的点表示的数总比左边的点表示的数大”,我们可以利用数形结合思想比较实数的大小.
知3-练
感悟新知
C
知识点
实数的大小比较
知4-导
感悟新知
4
利用数轴,我们可以比较两个有理数的大小.因为在数轴上表示的数,右边的数总比左边的数大.因为在数轴上3在2的右边,所以3>2,-2在-3的右边,所以-2___-3;
因为在数轴上
在
的右边,所以
__
,
-
在-
的右边,所以-
____-
,同理:0____
-
;
-
____-
.
知4-讲
结
论
感悟新知
在实数范围内,在数轴上表示的数,右边的数总比左边的数大.
知4-讲
感悟新知
正实数大于0,负实数小于0;正实数大于一切负实数;两个负实数比较大小,绝对值大的反而小.
知4-讲
感悟新知
比较下列各组数中两个数的大小:
例2
解:(1)因为
知4-讲
感悟新知
(2)因为
=10,π2=(3.141
5…)2,而10>3.152>π2,所以
>π.从而-
<-π.
知4-讲
总
结
感悟新知
当题目中直接比较大小较困难时,我们可以采用特殊值法,所取特殊值必须符合两个条件:
(1)在字母取值范围内;(2)求值计算简单,而求实数的相反数、倒数、绝对值的方法与求有理数的相反数、倒数、绝对值的方法是一样的.
知识点
实数的运算
知5-导
感悟新知
5
填空:设a,b,c是任意实数,则
(1)a+b=___________(加法交换律);
(2)(a+b)+c=___________(加法结合律);
(3)a+0=0+a
=___________;
(4)a+(-a)=(-a)+a=___________;
(5)ab=___________(乘法交换律);
(6)(ab)c=________(乘法结合律);
(7)1·a=a·1=________;
(8)a(b
+c)=________(乘法对于加法的分配律),
(b+c)a=________(乘法对于加法的分配律);
(9)实数的减法运算规定为a-b=a+____;
(10)对于每一个非零实数a,存在一个实数b,满足a·b=b·a=1,我们把b叫作a的________;
(11)实数的除法运算(除数b≠0),规定为a÷b=a·________;
(12)实数有一条重要性质:如果a≠0,b≠0,那么ab________0.
知5-导
感悟新知
知5-讲
感悟新知
1.在实数范围内,进行加、减、乘、除、乘方和开方运算时,有理数的运算法则和运算律仍然适用;实数混合运算的运算顺序与有理数的混合运算顺序一样,先算乘方、开方,再算乘除,最后算加减,同级运算按照自左向右的顺序进行,有括号先算括号里面的。
知5-讲
感悟新知
2.有理数的运算律在实数范围内仍然适用,在进行实数运算的过程中,要做到:一“看”——看算式的结构特点,能否运用运算律或公式;二“用”——运用运算律或公式;三“查”——检查过程和结果是否正确.
知5-讲
感悟新知
3.学法指南:实数的运算律
加法交换律:a+b=b+a;
加法结合律:(a+b)+c=a+(b+c);
乘法交换律:ab=ba;
乘法结合律:(ab)c
=a(bc);
乘法分配律:(a+b)c=ac
+bc.
知5-讲
感悟新知
要点精析:在实数范围内做开方运算时,要注意正实数和零既能开平方,也能开立方,负实数不能开平方.
(1)运算种类:
运算级别
第一级
第二级
第三级
运算名称
加
减
乘
除
乘方
平方
运算结果
和
差
积
商
幂
方根
知5-讲
感悟新知
(2)运算顺序:先乘方、开方,再乘除,最后算加减同级运算按照从左到右的顺序进行,有括号的先算括号里面的.
(3)运算律:与有理数运算律一致.
4.易错警示:(1)负实数只能开奇次方,不能开偶次方;
(2)计算结果中如果包含开方开不尽的数,则保留根号,结果要化为最简形式.
知5-讲
感悟新知
计算下列各式的值:
(加法结合律)
例
5
知5-讲
感悟新知
(乘法对于加法的分配律)
知5-讲
总
结
感悟新知
实数的运算同有理数的运算.实数运算中,无理数可选取近似值转化为有理数计算,中间结果所取的近似值要比结果要求多一位小数.
课堂小结
1.当数的范国从有理数扩充到实数后,有理教中关于相反数、例数和绝对值的相关性质同样适用于实数.
2.实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上一个点来表示,反过来敦轴上的任何一个点都表示一个实数.
实数
课堂小结
2.实数运算时要先确定运算符号及顺序,再进行运算,运算过程中要热练运用运算律及各种运算法则,掌握一定的运算技巧,同时要明确除开偶次方外,其他各种运算在实数范围内都能实施,且运算结果是唯一的;开偶次方只有在非负实数范围内才能实施,且正数的偶次方根有两个.
实数
课堂小结
运算种类:
运算级别
第一级
第二级
第三级
运算名称
加
减
乘
除
乘方
平方
运算结果
和
差
积
商
幂
方根
实数
课堂小结
3.易错警示:(1)负实数只能开奇次方,不能开偶次方;
(2)计算结果中如果包含开方开不尽的数,则保留根号,结果要化为最简形式.
实数
必做:
请完成教材课后习题
课后作业
作业
同课章节目录
