小学数学人教版五年级上1小数乘法课件(51张PPT)
文档属性
| 名称 | 小学数学人教版五年级上1小数乘法课件(51张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 11:38:21 | ||
图片预览








文档简介
1.1《小数乘整数》
试试看,你会做的
1.填空 。
3元=( )角 40角=( )元
5元6角=( )角 15角=( )元
2.计算。
46×30 313×53
复 习
村 居
草长莺飞二月天,
拂堤杨柳醉春烟。
儿童散学归来早,
忙趁东风放纸鸢。
走进风筝世界。
买3个 多少钱?
探究新知
1.广场售货亭卖几种风筝?他们买了哪一款?买了几
个?多少钱?列出算式。
2.对比今天的算式与以往的有什么不同,研究教材中
的三种算法,并尝试算一算。
3.对比哪种算法更简单,更接近我们以前学习的列竖
式计算。
自学提示
1 0 . 5
3 . 5
+
3 . 5
3 . 5
10.5(元)
3.5×3=
3.5元=3元5角
3元×3=9元
5角×3=15角
9元+15角=10.5元
探究新知
把3.5元看作35角。
3 . 5 元
×
3
1 0 . 5 元
3 5 角
×
3
1 0 5 角
3.5×3=
10.5(元)
探究新知
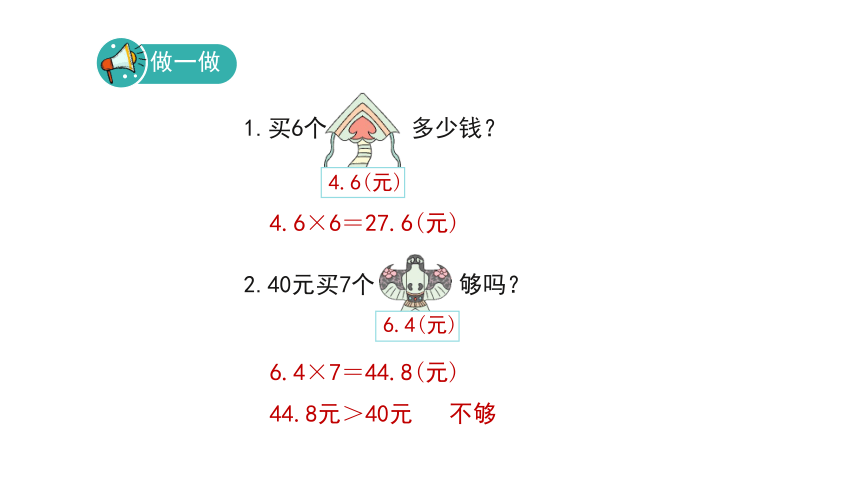
4.6×6=27.6(元)
6.4×7=44.8(元)
44.8元>40元 不够
做一做
1.买6个 多少钱?
4.6(元)
2.40元买7个 够吗?
6.4(元)
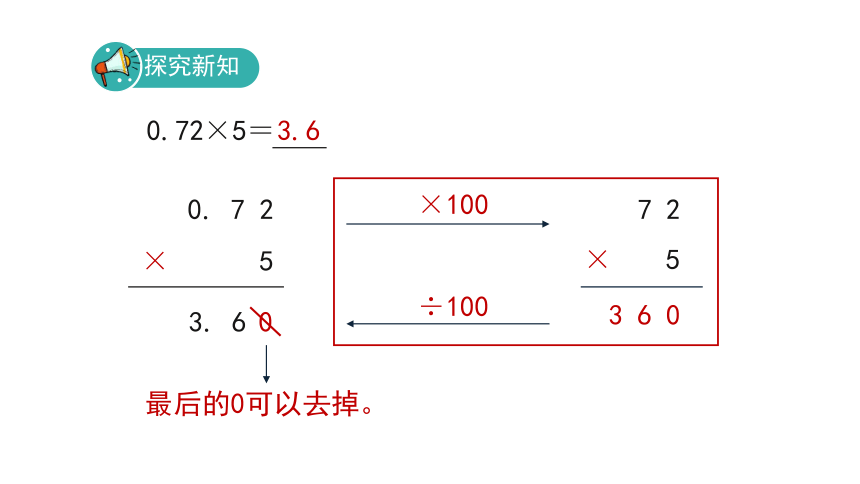
0.72×5=
0.72不是钱数,怎样计算?
能不能转化成整数来计算?
计算0.72×5可以先把0.72扩大到它的( )倍,变成整数,把算式变成( ),乘得的积是( ),要想使乘得的积不变,再把积缩小到它的( ),是( )。
填一填
探究新知
0.72×5=
3.6
3. 6
0. 7 2
×
5
7 2
×
5
3 6 0
×100
0
最后的0可以去掉。
÷100
探究新知
2 8
7
×
4
2 .8
0 .7
×
4
1 2 5
2 5
×
5
1 2 .5
2 .5
×
5
想一想:小数乘整数与整数乘整数有什么不同?
1.
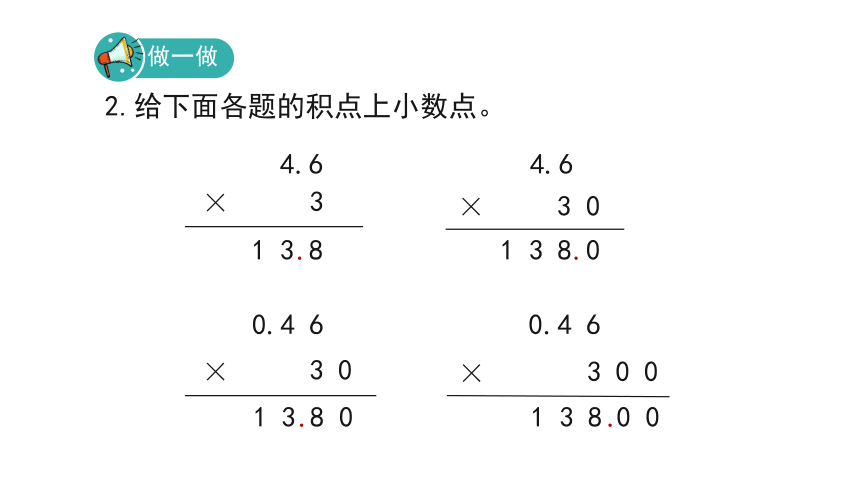
做一做
1 3 8
4.6
×
3
2.给下面各题的积点上小数点。
.
1 3 8 0
4.6
×
3 0
.
1 3 8 0
0.4 6
×
3 0
.
1 3 8 0 0
0.4 6
×
3 0 0
.
做一做
8 6.8
1 2.4
×
7
3.
2.3
×
1 2
4 6
2 3
2 7.6
1 2.3 0
2.0 5
×
6
3.1 3
×
5 3
9 3 9
1 5 6 5
1 6 5.8 9
做一做
1.2《小数乘小数》
例3:给一个长2.4m、宽0.8m的长方形宣传栏刷油漆,一共需要多少千克油漆?
探究新知
每平方米要用油漆0.9kg。
1.整合例3,要想求一共需要多少千克油漆,要先求什么?再求什么?列算式。
2.观察算式,因数有什么特点?研读书中方框里的步骤,体会是怎样计算的?
探究题纲
0.8米=8分米
将“米”改写成“分米”
2.4米=24分米
24×8=192(平方分米)
将积的单位“平方分米”改写成“平方米”:
192平方分米=1.92平方米
探究新知
方法一 转换单位计算。
先求长方形宣传栏的面积。
2.4×0.8=
2 . 4
扩大到它的10倍
扩大到它的10倍
缩小到它的
100
1
2 4
×
0 . 8
1 .9 2
×
8
1 9 2
1.92(平方米)
总结:小数乘小数,先把因数扩大相应的倍数,变成整数,然后按照整数乘法的计算方法算出积,再看因数中一共有几位小数,就从积的右边起数出几位,点上小数点。
方法二 转化成整数乘法计算。
探究新知
1.92×0.9=
1.9 2
扩大到它的100倍
扩大到它的10倍
缩小到它的
1000
1
1 9 2
×
0.9
1.7 2 8
×
9
1 7 2 8
1.728(kg)
答:一共需要1.728kg油漆。
再求一共需要多少千克油漆。
探究新知
2 .4
×
0. 8
1.9 2
1.9 2
×
0.9
1.7 2 8
一位小数
两位小数
一位小数
两位小数
三位小数
一位小数
探索规律
发现:两个因数的小数位数和等于积的小数位数。
0.56×0.04=
0
0. 5 6
×
0. 0 4
两位小数
两位小数
四位小数
0.0224
2 2 4
.
0
乘得的积的小数位数不够,要在前面用0补足,再点小数点。
例4:
探究新知
65.1×0.58 65.1
9.37 1.02×9.37
8.76×1 8.76×0.99
1×0.0001 0.01×0.01
1.在下面的 里填上“>”“<”或“=”。
练 习
<
<
=
>
2.(1)南美赤道地带的三趾蛞蝓是目前人们所知道的世界上爬行最慢的哺乳动物。它在地面上每分钟大约爬行2.1米,在树上爬行的速度是地面上的2.15倍。三趾蛞蝓在树上每分钟大约爬行多少米?
2.1×2.15=
4.515(米)
练 习
(2)一辆汽车从吉林到沈阳各路段行驶情况如下,填写表格并解答问题:
路 段
吉林----四平
四平----沈阳
行驶时间
4.7小时
3.1小时
平均速度
48千米∕时
62千米∕时
行驶路程
①如果这辆汽车每100千米耗油6.5升,从吉林到沈阳一共要耗油多少升?
225.6千米
192.2千米
(225.6+192.2)÷100×6.5=27.157(升)
练 习
这辆汽车从吉林到沈阳行驶了多长时间?4.7+3.1=7.8(时)
(答案不唯一)
②请你提出一个问题并解答。
1.3《倍数是小数的实际问题和乘法验算》
鸵鸟是世界上最大的鸟,成年后的鸵鸟体重约有130千克,身高2.5米以上。而非洲野狗体长1米左右,体重约25千克。
求一个数的几倍是多少,用( )法计算。
哎呀,它追上来了!
别担心,它追不上我!
非洲野狗的最高速度是56千米/时。
鸵鸟的最高速度是非洲野狗的1.3倍,鸵鸟的最高速度是多少千米/时?
探究新知
探究提纲
1.怎样列式求鸵鸟的速度?说出列式根据。
2.教材中给我们提供了哪几种验算方法?请你试
一试。
探究新知
1 6 8
5 6
×
1.3
5 6
7.2 8
56×1.3=
我算得对吗?
探究新知
1 6 8
5 6
×
1.3
5 6
7.2 8
56×1.3=
7 8
×
5 6
6 5
7 2.8
1.3
验算:
72.8(千米/时)
7 2.8
验算的方法
把因数的位置交换一下,再乘一遍,看对不对。
也可以用计算器来验算。
56×1.3,积应该比56大,所以肯定计算错了。
结合算式讨论:
1.在什么情况下,积小于第一个因数?
2.在什么情况下,积等于第一个因数?
3.在什么情况下,积大于第一个因数?
3.5×1.2=
3.5×0.8=
3.5×1=
3.5×0=
拓展延伸
做一做
下面各题的计算结果对吗?把不对的改正过来。
3.2×2.5=0.8
2.6×1.08=2.708
3.2×2.5=8
2.6×1.08=2.808
巩固应用
1×0.94 0.94 4.25×1.1 0.94
6×1.98 12 3.7×2.8 12
1.在下面的 里填上“>”“<”或“=”。
<
>
<
=
巩固应用
2.先计算,再验算。
0.39×2.9= 0.58×0.08= 3.7×200=
0.18×8.45= 4.5×0.002= 0.072×0.15=
1.4《积的近似数》
{5940675A-B579-460E-94D1-54222C63F5DA}
保留整数
保留一位小数
保留两位小数
4.076
1.517
6.7523
按要求用“四舍五入”法求出下面各小数的近似数。
4
4.1
4.08
2
1.5
1.52
7
6.8
6.75
复习旧知
从早到晚它看家,
见到主人摇尾巴。
嗅觉灵敏辨气味,
警察破案也找它。
猜谜语
人的嗅觉细胞约有0.049亿个,狗的嗅觉细胞个数是人的45倍,狗约有多少亿个嗅觉细胞?(得数保留一位小数。)
0.049×45≈ (亿个)
人的嗅觉细胞约有0.049亿个,狗的嗅觉细胞个数是人的45倍,狗约有多少亿个嗅觉细胞?(得数保留一位小数。)
自学提纲:
(1)图中的狗在做什么?你是从哪里看出来的?
(2)“求一个数的几倍是多少” 怎样列式?说出列式思路。
(3)得数保留一位小数,应该在哪位上“四舍五入”?总结求积的近
似值的方法。
0.049×45≈ (亿个)
2 4 5
0. 0 4 9
×
4 5
三位小数
1 9 6
2 2 0 5
.
0<5,舍去0和5,保留一位小数。
2.2
总结:求积的近似数,要先算出积,然后看要求保留的小数数位的下一位上的数字,再根据“四舍五入”法求积的近似数,最后用“≈”连接。
0
1.填空。
(1)求一个小数的近似数,如果保留三位小数,要看小数部分的第
( )位。
(2)3.124×58的积保留整数约是( );保留一位小数是( );
保留两位小数是( )。
2.判断。
(1)4.0和4的大小相等,精确度也相同。( )
(2)7.995精确到百分位约是8。( )
181.2
181.19
181
四
×
×
巩固新知
1.求积的近似数应注意什么?
(1)要看清题目要求。
(2)表示近似数时,小数末尾的“0”表示精确度,不能去掉。
(3)根据实际情况保留小数位数。如遇到有关付钱的题目且计算结果位数较
多时,要自觉地保留两位小数,即:精确到分。
(1)“四舍五入”到十分位。
(2)舍去十分位后面的尾数。
(3)得数保留一位小数。
2.求近似数的三种说法:(以得数保留一位小数为例)
1.5《整数乘法运算定律推广到小数》
7×12 12×7
=
(8×5)×4 8×(5×4)
(24+36)×5 24×5+36×5
=
=
我们学过的乘法运算定律都有什么?记得字母公式吗?
乘法交换律:a×b=b×a
乘法结合律:(a×b)×c=a×(b×c)
乘法分配律:(a+b)c=ac+bc
观察下面每组的两个算式,它们有什么关系?分别运用了什么运算定律?
复习旧知
小数四则混合运算的顺序跟整数是一样的。
观察下面每组的两个算式,它们有什么关系?
从上面的算式中,你发现了什么规律?
0.7×1.2 1.2×0.7
(0.8×0.5)×0.4 0.8×(0.5×0.4)
(2.4+3.6)×0.5 2.4×0.5+3.6×0.5
=
=
=
探究新知
整数乘法的这些运算定律是否适用于小数乘法呢——( )
适 用
交换律
结合律
分配律
应用乘法的运算定律,可以使一些计算简便。
?
小数乘法的运算定律有:
小窍门
小数乘法应用运算定律简算时,要考虑怎样变化才能使计算时小数变成整数。
例如:
1.6×25=4×(0.4×25)
10.8×125=(10+0.8)×125
这道题运用了乘法的什么运算定律?
这道题运用了乘法的什么运算定律?
=4.78
=130+1.3
=1×4.78
=0.65×200+0.65×2
=0.25×4×4.78
=0.65×(200+2)
0.25×4.78×4
0.65×202
=131.3
交换律、结合律
分配律
探究新知
1.根据运算定律填空。
4.2×1.69= ×
2.5×(0.77×0.4)=( × )×
7.2×8.4+2.8×8.4=( + )×
做一做
2.用简便方法计算下面各题。
0.034×0.5×0.6 101×0.45
4.75×99+4.75 2.73×99
做一做
用简便方法计算下面各题。
4.8×0.25 0.78×98
0.5×2.33×8 1.5×105
0.3×2.5×0.4 1.2×2.5+0.8×2.5
巩固练习
试试看,你会做的
1.填空 。
3元=( )角 40角=( )元
5元6角=( )角 15角=( )元
2.计算。
46×30 313×53
复 习
村 居
草长莺飞二月天,
拂堤杨柳醉春烟。
儿童散学归来早,
忙趁东风放纸鸢。
走进风筝世界。
买3个 多少钱?
探究新知
1.广场售货亭卖几种风筝?他们买了哪一款?买了几
个?多少钱?列出算式。
2.对比今天的算式与以往的有什么不同,研究教材中
的三种算法,并尝试算一算。
3.对比哪种算法更简单,更接近我们以前学习的列竖
式计算。
自学提示
1 0 . 5
3 . 5
+
3 . 5
3 . 5
10.5(元)
3.5×3=
3.5元=3元5角
3元×3=9元
5角×3=15角
9元+15角=10.5元
探究新知
把3.5元看作35角。
3 . 5 元
×
3
1 0 . 5 元
3 5 角
×
3
1 0 5 角
3.5×3=
10.5(元)
探究新知
4.6×6=27.6(元)
6.4×7=44.8(元)
44.8元>40元 不够
做一做
1.买6个 多少钱?
4.6(元)
2.40元买7个 够吗?
6.4(元)
0.72×5=
0.72不是钱数,怎样计算?
能不能转化成整数来计算?
计算0.72×5可以先把0.72扩大到它的( )倍,变成整数,把算式变成( ),乘得的积是( ),要想使乘得的积不变,再把积缩小到它的( ),是( )。
填一填
探究新知
0.72×5=
3.6
3. 6
0. 7 2
×
5
7 2
×
5
3 6 0
×100
0
最后的0可以去掉。
÷100
探究新知
2 8
7
×
4
2 .8
0 .7
×
4
1 2 5
2 5
×
5
1 2 .5
2 .5
×
5
想一想:小数乘整数与整数乘整数有什么不同?
1.
做一做
1 3 8
4.6
×
3
2.给下面各题的积点上小数点。
.
1 3 8 0
4.6
×
3 0
.
1 3 8 0
0.4 6
×
3 0
.
1 3 8 0 0
0.4 6
×
3 0 0
.
做一做
8 6.8
1 2.4
×
7
3.
2.3
×
1 2
4 6
2 3
2 7.6
1 2.3 0
2.0 5
×
6
3.1 3
×
5 3
9 3 9
1 5 6 5
1 6 5.8 9
做一做
1.2《小数乘小数》
例3:给一个长2.4m、宽0.8m的长方形宣传栏刷油漆,一共需要多少千克油漆?
探究新知
每平方米要用油漆0.9kg。
1.整合例3,要想求一共需要多少千克油漆,要先求什么?再求什么?列算式。
2.观察算式,因数有什么特点?研读书中方框里的步骤,体会是怎样计算的?
探究题纲
0.8米=8分米
将“米”改写成“分米”
2.4米=24分米
24×8=192(平方分米)
将积的单位“平方分米”改写成“平方米”:
192平方分米=1.92平方米
探究新知
方法一 转换单位计算。
先求长方形宣传栏的面积。
2.4×0.8=
2 . 4
扩大到它的10倍
扩大到它的10倍
缩小到它的
100
1
2 4
×
0 . 8
1 .9 2
×
8
1 9 2
1.92(平方米)
总结:小数乘小数,先把因数扩大相应的倍数,变成整数,然后按照整数乘法的计算方法算出积,再看因数中一共有几位小数,就从积的右边起数出几位,点上小数点。
方法二 转化成整数乘法计算。
探究新知
1.92×0.9=
1.9 2
扩大到它的100倍
扩大到它的10倍
缩小到它的
1000
1
1 9 2
×
0.9
1.7 2 8
×
9
1 7 2 8
1.728(kg)
答:一共需要1.728kg油漆。
再求一共需要多少千克油漆。
探究新知
2 .4
×
0. 8
1.9 2
1.9 2
×
0.9
1.7 2 8
一位小数
两位小数
一位小数
两位小数
三位小数
一位小数
探索规律
发现:两个因数的小数位数和等于积的小数位数。
0.56×0.04=
0
0. 5 6
×
0. 0 4
两位小数
两位小数
四位小数
0.0224
2 2 4
.
0
乘得的积的小数位数不够,要在前面用0补足,再点小数点。
例4:
探究新知
65.1×0.58 65.1
9.37 1.02×9.37
8.76×1 8.76×0.99
1×0.0001 0.01×0.01
1.在下面的 里填上“>”“<”或“=”。
练 习
<
<
=
>
2.(1)南美赤道地带的三趾蛞蝓是目前人们所知道的世界上爬行最慢的哺乳动物。它在地面上每分钟大约爬行2.1米,在树上爬行的速度是地面上的2.15倍。三趾蛞蝓在树上每分钟大约爬行多少米?
2.1×2.15=
4.515(米)
练 习
(2)一辆汽车从吉林到沈阳各路段行驶情况如下,填写表格并解答问题:
路 段
吉林----四平
四平----沈阳
行驶时间
4.7小时
3.1小时
平均速度
48千米∕时
62千米∕时
行驶路程
①如果这辆汽车每100千米耗油6.5升,从吉林到沈阳一共要耗油多少升?
225.6千米
192.2千米
(225.6+192.2)÷100×6.5=27.157(升)
练 习
这辆汽车从吉林到沈阳行驶了多长时间?4.7+3.1=7.8(时)
(答案不唯一)
②请你提出一个问题并解答。
1.3《倍数是小数的实际问题和乘法验算》
鸵鸟是世界上最大的鸟,成年后的鸵鸟体重约有130千克,身高2.5米以上。而非洲野狗体长1米左右,体重约25千克。
求一个数的几倍是多少,用( )法计算。
哎呀,它追上来了!
别担心,它追不上我!
非洲野狗的最高速度是56千米/时。
鸵鸟的最高速度是非洲野狗的1.3倍,鸵鸟的最高速度是多少千米/时?
探究新知
探究提纲
1.怎样列式求鸵鸟的速度?说出列式根据。
2.教材中给我们提供了哪几种验算方法?请你试
一试。
探究新知
1 6 8
5 6
×
1.3
5 6
7.2 8
56×1.3=
我算得对吗?
探究新知
1 6 8
5 6
×
1.3
5 6
7.2 8
56×1.3=
7 8
×
5 6
6 5
7 2.8
1.3
验算:
72.8(千米/时)
7 2.8
验算的方法
把因数的位置交换一下,再乘一遍,看对不对。
也可以用计算器来验算。
56×1.3,积应该比56大,所以肯定计算错了。
结合算式讨论:
1.在什么情况下,积小于第一个因数?
2.在什么情况下,积等于第一个因数?
3.在什么情况下,积大于第一个因数?
3.5×1.2=
3.5×0.8=
3.5×1=
3.5×0=
拓展延伸
做一做
下面各题的计算结果对吗?把不对的改正过来。
3.2×2.5=0.8
2.6×1.08=2.708
3.2×2.5=8
2.6×1.08=2.808
巩固应用
1×0.94 0.94 4.25×1.1 0.94
6×1.98 12 3.7×2.8 12
1.在下面的 里填上“>”“<”或“=”。
<
>
<
=
巩固应用
2.先计算,再验算。
0.39×2.9= 0.58×0.08= 3.7×200=
0.18×8.45= 4.5×0.002= 0.072×0.15=
1.4《积的近似数》
{5940675A-B579-460E-94D1-54222C63F5DA}
保留整数
保留一位小数
保留两位小数
4.076
1.517
6.7523
按要求用“四舍五入”法求出下面各小数的近似数。
4
4.1
4.08
2
1.5
1.52
7
6.8
6.75
复习旧知
从早到晚它看家,
见到主人摇尾巴。
嗅觉灵敏辨气味,
警察破案也找它。
猜谜语
人的嗅觉细胞约有0.049亿个,狗的嗅觉细胞个数是人的45倍,狗约有多少亿个嗅觉细胞?(得数保留一位小数。)
0.049×45≈ (亿个)
人的嗅觉细胞约有0.049亿个,狗的嗅觉细胞个数是人的45倍,狗约有多少亿个嗅觉细胞?(得数保留一位小数。)
自学提纲:
(1)图中的狗在做什么?你是从哪里看出来的?
(2)“求一个数的几倍是多少” 怎样列式?说出列式思路。
(3)得数保留一位小数,应该在哪位上“四舍五入”?总结求积的近
似值的方法。
0.049×45≈ (亿个)
2 4 5
0. 0 4 9
×
4 5
三位小数
1 9 6
2 2 0 5
.
0<5,舍去0和5,保留一位小数。
2.2
总结:求积的近似数,要先算出积,然后看要求保留的小数数位的下一位上的数字,再根据“四舍五入”法求积的近似数,最后用“≈”连接。
0
1.填空。
(1)求一个小数的近似数,如果保留三位小数,要看小数部分的第
( )位。
(2)3.124×58的积保留整数约是( );保留一位小数是( );
保留两位小数是( )。
2.判断。
(1)4.0和4的大小相等,精确度也相同。( )
(2)7.995精确到百分位约是8。( )
181.2
181.19
181
四
×
×
巩固新知
1.求积的近似数应注意什么?
(1)要看清题目要求。
(2)表示近似数时,小数末尾的“0”表示精确度,不能去掉。
(3)根据实际情况保留小数位数。如遇到有关付钱的题目且计算结果位数较
多时,要自觉地保留两位小数,即:精确到分。
(1)“四舍五入”到十分位。
(2)舍去十分位后面的尾数。
(3)得数保留一位小数。
2.求近似数的三种说法:(以得数保留一位小数为例)
1.5《整数乘法运算定律推广到小数》
7×12 12×7
=
(8×5)×4 8×(5×4)
(24+36)×5 24×5+36×5
=
=
我们学过的乘法运算定律都有什么?记得字母公式吗?
乘法交换律:a×b=b×a
乘法结合律:(a×b)×c=a×(b×c)
乘法分配律:(a+b)c=ac+bc
观察下面每组的两个算式,它们有什么关系?分别运用了什么运算定律?
复习旧知
小数四则混合运算的顺序跟整数是一样的。
观察下面每组的两个算式,它们有什么关系?
从上面的算式中,你发现了什么规律?
0.7×1.2 1.2×0.7
(0.8×0.5)×0.4 0.8×(0.5×0.4)
(2.4+3.6)×0.5 2.4×0.5+3.6×0.5
=
=
=
探究新知
整数乘法的这些运算定律是否适用于小数乘法呢——( )
适 用
交换律
结合律
分配律
应用乘法的运算定律,可以使一些计算简便。
?
小数乘法的运算定律有:
小窍门
小数乘法应用运算定律简算时,要考虑怎样变化才能使计算时小数变成整数。
例如:
1.6×25=4×(0.4×25)
10.8×125=(10+0.8)×125
这道题运用了乘法的什么运算定律?
这道题运用了乘法的什么运算定律?
=4.78
=130+1.3
=1×4.78
=0.65×200+0.65×2
=0.25×4×4.78
=0.65×(200+2)
0.25×4.78×4
0.65×202
=131.3
交换律、结合律
分配律
探究新知
1.根据运算定律填空。
4.2×1.69= ×
2.5×(0.77×0.4)=( × )×
7.2×8.4+2.8×8.4=( + )×
做一做
2.用简便方法计算下面各题。
0.034×0.5×0.6 101×0.45
4.75×99+4.75 2.73×99
做一做
用简便方法计算下面各题。
4.8×0.25 0.78×98
0.5×2.33×8 1.5×105
0.3×2.5×0.4 1.2×2.5+0.8×2.5
巩固练习
