北师大数学6年级下册学案_6.4.3画一画
文档属性
| 名称 | 北师大数学6年级下册学案_6.4.3画一画 |
|
|
| 格式 | docx | ||
| 文件大小 | 77.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 13:48:13 | ||
图片预览


文档简介
6.4.4画一画
【知识回顾】
成正比例中的两个量,一个量变化,另一个量也随着变化,而且这两个变化的量相对应的比值一定。
成正比例关系的两个量中,一个量扩大到原来的几倍(或缩小到原来的几分之几),另一个量也扩大到原来的几倍(或缩小到原来的几分之几)。
【知识讲解】
【知识点】正比例图像
成正比例的两个变量的点会在同一条直线上。
正比例的图像所在的直线经过原点。
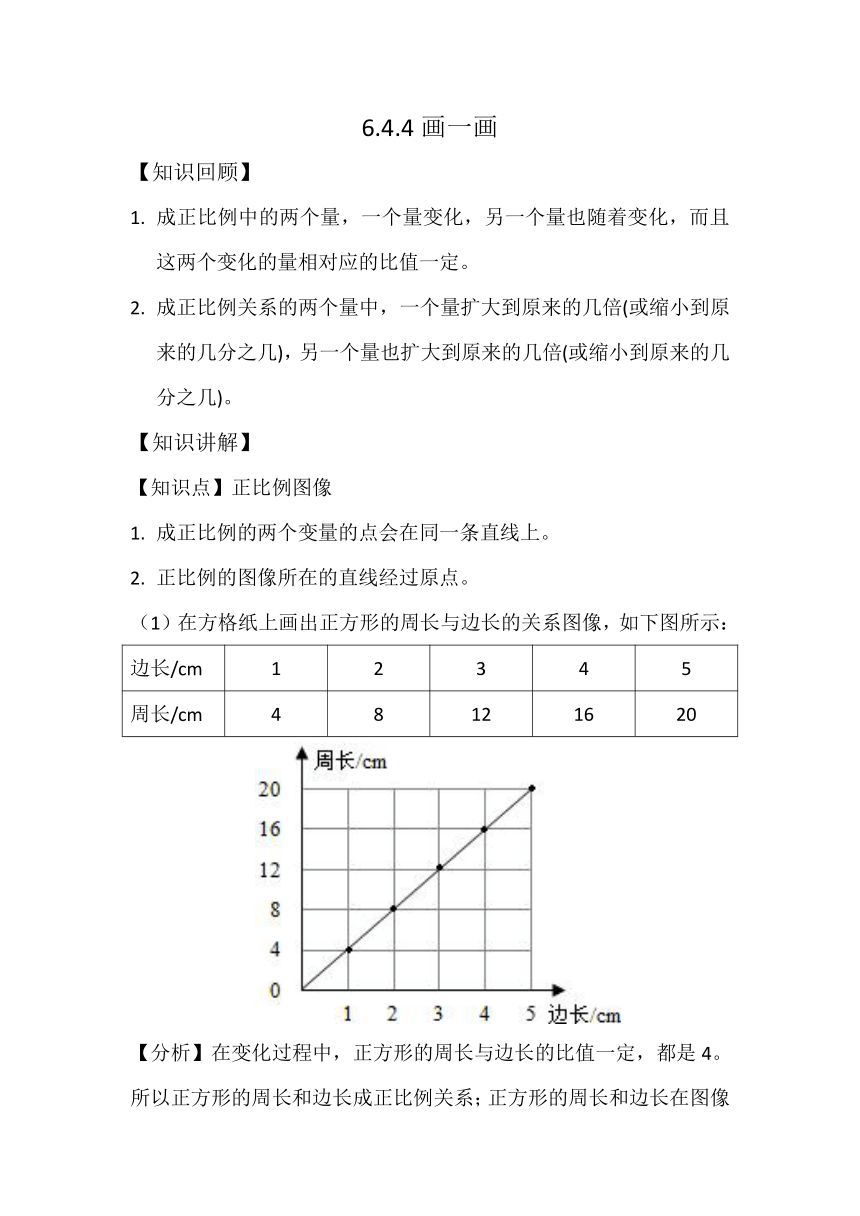
(1)在方格纸上画出正方形的周长与边长的关系图像,如下图所示:
边长/cm
1
2
3
4
5
周长/cm
4
8
12
16
20
【分析】在变化过程中,正方形的周长与边长的比值一定,都是4。所以正方形的周长和边长成正比例关系;正方形的周长和边长在图像中表示的点能连成一条直线。
(2)如果有一个点A(20,80),它会在这条直线上吗?
解析:点A的意思是正方形的边长是20cm,它的周长就是80cm。周长与边长的比也是4,所以点A在这条直线上。
【拓展应用】
1.正比例图像经过原点,在x=0时,y=kx=0,注意:k不能等于0。
2. y=kx, K等于0,x取任何值,y都等于0,此时就不呈正比例。
【牛刀小试】
1.一个人的身高和年龄成正比例关系(×)。
2.宽不变,长方形的周长与长成正比例关系(×)。
【典型例题】
1.买邮票的枚数与应付的钱数成正比例吗?
【思路点拨】分析:成正比例的两个量,一个量变化,另一个量也随着变化,而且这两个变化的量相对应的比值一定。
【解析】买邮票应付的钱数÷购买的枚数=邮票的单价,邮票的单价不变。应付的钱数随购买的枚数的变化而变化,而且比值不变。所以应付的钱数与买邮票的枚数成正比例。
2.已知一辆汽车行驶的路程和时间如下表,把下表填写完整,判断这辆汽车在这段时间内行驶的路程和时间是否成正比例关系。并画出它的路程和时间关系图像,观察一下有什么特点。
时间/h
1
2
3
4
5
6
路程/km
300
600
900
【思路点拨】分析:要判断两个量是否为正比例关系,要看这两个量的比值是否一定。如果比值一定,就成正比例。题中路程与时间的比值就是该辆汽车的行驶速度
【解析】速度=路程÷时间=300÷1=600÷2=900÷3=300(km/h),300是定值,所以这辆汽车在这段时间内行驶的路程和时间成正比例关系。根据路程=速度×时间,
当时间=4时,路程=300×4=1200(km);
当时间=5时,路程=300×5=1500(km);
当时间=6时,路程=300×6=1800(km);填表如下:
时间/h
1
2
3
4
5
6
路程/km
300
600
900
1200
1500
1800
路程与时间关系图像如下:
观察图像可得:这辆汽车行驶的路程随时间的增加而增大,路程和时间在图像中表示的点能连成一条直线,并且经过原点。原点(0,0)代表的意思是汽车行驶0小时,路程也为0。
【知识小结】
本节课结合丰富的事例,进一步认识正比例。掌握成正比例的量的变化规律及其图象的特征。根据正比例的意义,正确判断两个相关联的量是不是成正比例。
【知识回顾】
成正比例中的两个量,一个量变化,另一个量也随着变化,而且这两个变化的量相对应的比值一定。
成正比例关系的两个量中,一个量扩大到原来的几倍(或缩小到原来的几分之几),另一个量也扩大到原来的几倍(或缩小到原来的几分之几)。
【知识讲解】
【知识点】正比例图像
成正比例的两个变量的点会在同一条直线上。
正比例的图像所在的直线经过原点。
(1)在方格纸上画出正方形的周长与边长的关系图像,如下图所示:
边长/cm
1
2
3
4
5
周长/cm
4
8
12
16
20
【分析】在变化过程中,正方形的周长与边长的比值一定,都是4。所以正方形的周长和边长成正比例关系;正方形的周长和边长在图像中表示的点能连成一条直线。
(2)如果有一个点A(20,80),它会在这条直线上吗?
解析:点A的意思是正方形的边长是20cm,它的周长就是80cm。周长与边长的比也是4,所以点A在这条直线上。
【拓展应用】
1.正比例图像经过原点,在x=0时,y=kx=0,注意:k不能等于0。
2. y=kx, K等于0,x取任何值,y都等于0,此时就不呈正比例。
【牛刀小试】
1.一个人的身高和年龄成正比例关系(×)。
2.宽不变,长方形的周长与长成正比例关系(×)。
【典型例题】
1.买邮票的枚数与应付的钱数成正比例吗?
【思路点拨】分析:成正比例的两个量,一个量变化,另一个量也随着变化,而且这两个变化的量相对应的比值一定。
【解析】买邮票应付的钱数÷购买的枚数=邮票的单价,邮票的单价不变。应付的钱数随购买的枚数的变化而变化,而且比值不变。所以应付的钱数与买邮票的枚数成正比例。
2.已知一辆汽车行驶的路程和时间如下表,把下表填写完整,判断这辆汽车在这段时间内行驶的路程和时间是否成正比例关系。并画出它的路程和时间关系图像,观察一下有什么特点。
时间/h
1
2
3
4
5
6
路程/km
300
600
900
【思路点拨】分析:要判断两个量是否为正比例关系,要看这两个量的比值是否一定。如果比值一定,就成正比例。题中路程与时间的比值就是该辆汽车的行驶速度
【解析】速度=路程÷时间=300÷1=600÷2=900÷3=300(km/h),300是定值,所以这辆汽车在这段时间内行驶的路程和时间成正比例关系。根据路程=速度×时间,
当时间=4时,路程=300×4=1200(km);
当时间=5时,路程=300×5=1500(km);
当时间=6时,路程=300×6=1800(km);填表如下:
时间/h
1
2
3
4
5
6
路程/km
300
600
900
1200
1500
1800
路程与时间关系图像如下:
观察图像可得:这辆汽车行驶的路程随时间的增加而增大,路程和时间在图像中表示的点能连成一条直线,并且经过原点。原点(0,0)代表的意思是汽车行驶0小时,路程也为0。
【知识小结】
本节课结合丰富的事例,进一步认识正比例。掌握成正比例的量的变化规律及其图象的特征。根据正比例的意义,正确判断两个相关联的量是不是成正比例。
