1.2定义与命题——1.3证明 同步练习(含解析)
文档属性
| 名称 | 1.2定义与命题——1.3证明 同步练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-16 22:08:22 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
三角形的初步知识——1.2+1.3定义与证明
一.选择题(共10小题)
1.(2021春?滑县期末)下列说法中,属于真命题的是
A.垂线最短
B.在同一平面内,过一点有且只有一条直线与已知直线垂直
C.相等的角一定是对顶角
D.两直线相交,邻补角相等
2.(2021春?峄城区期末)如图,在中,是边上的高,是的角平分线,若,,则的度数为
A.
B.
C.
D.
3.(2021春?莱州市期末)下列命题正确的是
A.若,则
B.若,则
C.若,则
D.若,则
4.(2021春?海口期末)如图,已知平分,交于点,过点作于点.若比大,则的度数是
A.
B.
C.
D.不能确定
5.(2021春?兴隆县期末)中,,,平分,点为上一点,于点,则的度数为
A.5
B.10
C.12
D.20
6.(2021春?福田区校级月考)如图,的高、相交于点,如果,那么的大小为
A.
B.
C.
D.
7.(2021春?碑林区校级期中)如图,,为的高线,角平分线,于点.当,时,的度数为
A.
B.
C.
D.
8.(2021春?高州市期末)如图,小明从一张三角形纸片的边上选取一点,将纸片沿着对折一次使得点落在处后,再将纸片沿着对折一次,使得点落在上的处,已知,,则原三角形的的度数为
A.
B.
C.
D.
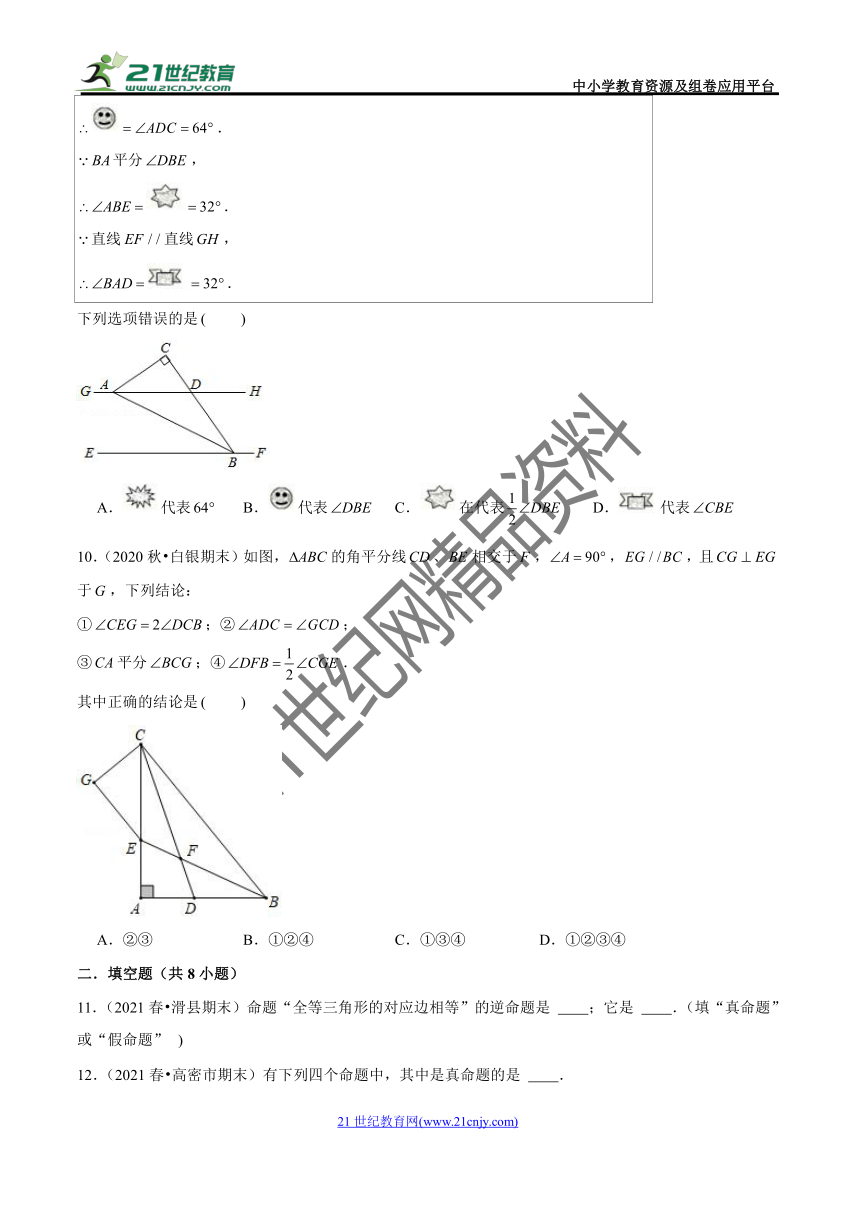
9.(2020秋?章丘区期末)下面是投影屏上出示的解答题,需要回答横线上符号代表的内容.
如图,直线直线,在中,,顶点在上,顶点在上,且平分,若,求的度数.
解:,,
.
直线直线,
.
平分,
.
直线直线,
.
下列选项错误的是
A.代表
B.代表
C.在代表
D.代表
10.(2020秋?白银期末)如图,的角平分线、相交于,,,且于,下列结论:
①;②;
③平分;④.
其中正确的结论是
A.②③
B.①②④
C.①③④
D.①②③④
二.填空题(共8小题)
11.(2021春?滑县期末)命题“全等三角形的对应边相等”的逆命题是
;它是
.(填“真命题”或“假命题”
12.(2021春?高密市期末)有下列四个命题中,其中是真命题的是
.
.弧分为优弧和劣弧
.经过圆心的弦是直径
.若一个角的两边与另一个角的两边互相平行,则这两个角相等或互补
.三角形的一个外角大于三角形的每一个内角
13.(2021春?滦州市期末)已知:如图,是中边上的高,平分,若,,则 度.
14.(2021春?灵石县期末)如图,已知是的角平分线,,垂足为,交于,则下列命题:①,②,③,④,其中正确的是
.
15.(2021春?开州区期末)请将命题“坐标轴上的点至少有一个坐标为0”改写成“如果那么”的形式: .
16.(2021春?东坡区期末)如图中,、分别在边、上,将沿直线翻折后使点与点相重合.若,,则 .
17.(2021春?新都区期末)如图,将沿、翻折,使顶点、都落于点处,且线段、翻折后重合于,若,则 度.
18.(2021春?宽城区期末)将一副直角三角尺按如图所示的方式摆放,则的大小为
度.
三.解答题(共6小题)
19.(2021春?靖江市期末)如图,在四边形中,①,②,③.
(1)请你以其中两个为条件,第三个为结论,写出一个命题;
(2)判断这个命题是否为真命题,并说明理由.
20.(2021春?临西县期末)对于命题“相等的角是直角”,解决下列问题.
(1)指出命题的条件和结论,并改写成“如果那么”的形式;
(2)判断此命题是真命题还是假命题.
21.(2020春?博兴县期末)如图,有以下四个条件:①,②,③平分,④平分.
(1)若平分,,,求证:平分.
(2)除(1)外,请再选择四个条件中的三个作为题设,余下的一个作为结论,写出一个真命题,再给予证明.
22.(2019秋?太原期末)阅读下面内容,并解答问题.
在学行线的性质后,老师请学们证明命题:两条平行线被第三条直线所截,一组同旁内角的平分线互相垂直.
小颖根据命题画出图形并写出如下的已知条件.
已知:如图1,,直线分别交,于点,.的平分线与的平分线交于点.求证: .
(1)请补充要求证的结论,并写出证明过程;
(2)请从下列、两题中任选一题作答,我选择 题.
.在图1的基础上,分别作的平分线与的平分线交于点,得到图2,则的度数为 .
.如图3,,直线分别交,于点,.点在直线,之间,且在直线右侧,的平分线与的平分线交于点,则与满足的数量关系为 .
23.(2021春?长安区期末)如图1和图2,在三角形纸片中,点,分别在边,上,沿折叠,点落在点的位置.
(1)如图1,当点落在边上时,与之间的数量关系为
(只填序号),并说明理由;
①
②
③
(2)如图2,当点落在内部时,直接写出与,之间的数量关系.
24.(2021春?长春期末)规律探索探索三角形的内(外角平分线形成的角的规律:
在三角形中,由三角形的内角平分线外角平分线所形成的角存在一定的规律.
规律1:三角形的两个内角的平分线形成的钝角等于加上第三个内角度数的一半;
规律2:三角形的两个外角的平分线形成的锐角等于减去与这两个外角不相邻的内角度数的一半.
问题呈现如图①,点是的内角平分线与的交点,点是的外角平分线与的交点,则,.
说明如下:
、是的角平分线,
,.
.①
.
.
请你仔细阅读理解上面的说理过程,完成下列问题:
(1)上述说理过程中步骤①的依据是
.
(2)结合图①,写出说明的说理过程.
拓展延伸如图②,点是的内角平分线与的外角平分线的交点.若,则的大小为
度.
三角形的初步知识——1.2+1.3定义与证明
参考答案与试题解析
一.选择题(共10小题)
1.(2021春?滑县期末)下列说法中,属于真命题的是
A.垂线最短
B.在同一平面内,过一点有且只有一条直线与已知直线垂直
C.相等的角一定是对顶角
D.两直线相交,邻补角相等
【解答】解:、垂线段最短是真命题,垂线最短不是真命题,即不是真命题;
、在同一平面内,过一点有且只有一条直线与已知直线垂直,为真命题;
、对顶角一定相等,但相等的角不一定都是对顶角,相等的角一定是对顶角不正确,即不是真命题;
、两直线相交,同角的补角一定相等,邻补角相等不正确,即不是真命题.
故选:.
2.(2021春?峄城区期末)如图,在中,是边上的高,是的角平分线,若,,则的度数为
A.
B.
C.
D.
【解答】解:,,
.
是的角平分线,
.
.
是边上的高,
.
.
.
故选:.
3.(2021春?莱州市期末)下列命题正确的是
A.若,则
B.若,则
C.若,则
D.若,则
【解答】解:、若,则,原命题是假命题;
、若,,则,原命题是假命题;
、若,,则,原命题是假命题;
、若,则,是真命题;
故选:.
4.(2021春?海口期末)如图,已知平分,交于点,过点作于点.若比大,则的度数是
A.
B.
C.
D.不能确定
【解答】解:由题意知:.
平分,
.
又,
.
.
又,
.
.
.
,
.
,
.
故选:.
5.(2021春?兴隆县期末)中,,,平分,点为上一点,于点,则的度数为
A.5
B.10
C.12
D.20
【解答】解:,,
,
是的平分线,
,
,
又,
,
,
故选:.
6.(2021春?福田区校级月考)如图,的高、相交于点,如果,那么的大小为
A.
B.
C.
D.
【解答】解:如图,
、均为的高,
,
,
,
则.
故选:.
7.(2021春?碑林区校级期中)如图,,为的高线,角平分线,于点.当,时,的度数为
A.
B.
C.
D.
【解答】解:,
,
又,
,
又,
,
又平分,
,
,
故选:.
8.(2021春?高州市期末)如图,小明从一张三角形纸片的边上选取一点,将纸片沿着对折一次使得点落在处后,再将纸片沿着对折一次,使得点落在上的处,已知,,则原三角形的的度数为
A.
B.
C.
D.
【解答】解:如图,
由题意得:△,△.
,,.
.
.
又,
.
又,
.
.
.
.
故选:.
9.(2020秋?章丘区期末)下面是投影屏上出示的解答题,需要回答横线上符号代表的内容.
如图,直线直线,在中,,顶点在上,顶点在上,且平分,若,求的度数.
解:,,
.
直线直线,
.
平分,
.
直线直线,
.
下列选项错误的是
A.代表
B.代表
C.在代表
D.代表
【解答】解:,,
.
直线直线,
.
平分,
.
直线直线,
.
故选:.
10.(2020秋?白银期末)如图,的角平分线、相交于,,,且于,下列结论:
①;
②;
③平分;
④.
其中正确的结论是
A.②③
B.①②④
C.①③④
D.①②③④
【解答】解:,
,
平分,
,
,故①正确,
,
,
,
,
,
,
,
,,,
,故②正确,
假设平分,则,
,显然不符合题意,故③错误,
,,
,故④正确,
故选:.
二.填空题(共8小题)
11.(2021春?滑县期末)命题“全等三角形的对应边相等”的逆命题是
三边对应相等的三角形全等 ;它是
.(填“真命题”或“假命题”
【解答】解:命题“全等三角形的对应边相等”的逆命题是三边对应相等的三角形全等,逆命题是真命题;
故答案为:三边对应相等的三角形全等;真命题.
12.(2021春?高密市期末)有下列四个命题中,其中是真命题的是
, .
.弧分为优弧和劣弧
.经过圆心的弦是直径
.若一个角的两边与另一个角的两边互相平行,则这两个角相等或互补
.三角形的一个外角大于三角形的每一个内角
【解答】解:.弧分为优弧和劣弧,是假命题,弧分为优弧和劣弧,半圆.
.经过圆心的弦是直径,是真命题.
.若一个角的两边与另一个角的两边互相平行,则这两个角相等或互补,是真命题.
.三角形的一个外角大于三角形的每一个内角,是假命题.三角形的一个外角大于任何一个和他不相邻内角.
故答案为:,.
13.(2021春?滦州市期末)已知:如图,是中边上的高,平分,若,,则 14 度.
【解答】解:,,
.
是中边上的高,
.
平分,
.
,
,
.
故答案为:14.
14.(2021春?灵石县期末)如图,已知是的角平分线,,垂足为,交于,则下列命题:①,②,③,④,其中正确的是
①②③④ .
【解答】解:是的角平分线,
,
,
,
,,
,
,
,
,
,
故①②③④正确,
故答案为:①②③④
15.(2021春?开州区期末)请将命题“坐标轴上的点至少有一个坐标为0”改写成“如果那么”的形式: 如果一个点在坐标轴上,那么这个点至少有一个坐标为0 .
【解答】解:将命题“坐标轴上的点至少有一个坐标为0”改写成“如果那么”的形式:如果一个点在坐标轴上,那么这个点至少有一个坐标为0.
故答案为:如果一个点在坐标轴上,那么这个点至少有一个坐标为0.
16.(2021春?东坡区期末)如图中,、分别在边、上,将沿直线翻折后使点与点相重合.若,,则 .
【解答】解:由折叠可知:,,
,,
,
,
,
故答案为.
17.(2021春?新都区期末)如图,将沿、翻折,使顶点、都落于点处,且线段、翻折后重合于,若,则 63 度.
【解答】解:连接、,如图所示:
由折叠的性质得:,
,,
又由折叠的性质得:,,
,,
,,,
,
,
,
,
故答案为:63.
18.(2021春?宽城区期末)将一副直角三角尺按如图所示的方式摆放,则的大小为
75 度.
【解答】解:,
故答案为:75.
三.解答题(共6小题)
19.(2021春?靖江市期末)如图,在四边形中,①,②,③.
(1)请你以其中两个为条件,第三个为结论,写出一个命题;
(2)判断这个命题是否为真命题,并说明理由.
【解答】解:(1)如果,,那么;
(2)这个命题是真命题,
证明:,
,
,
,
.
20.(2021春?临西县期末)对于命题“相等的角是直角”,解决下列问题.
(1)指出命题的条件和结论,并改写成“如果那么”的形式;
(2)判断此命题是真命题还是假命题.
【解答】解:(1)命题“相等的角是直角”的条件是两个角是相等;结论是这两个角是直角,
改写成“如果那么”的形式为:如果两个角相等,那么这两个角都是直角;
(2)“相等的角是直角”是假命题.
21.(2020春?博兴县期末)如图,有以下四个条件:①,②,③平分,④平分.
(1)若平分,,,求证:平分.
(2)除(1)外,请再选择四个条件中的三个作为题设,余下的一个作为结论,写出一个真命题,再给予证明.
【解答】(1)证明:平分,
,
,
,,
,
,
,即平分.
(2)解:如果平分,,,那么平分.
证明:平分,
,
,
,,
,
,
,即平分.
22.(2019秋?太原期末)阅读下面内容,并解答问题.
在学行线的性质后,老师请学们证明命题:两条平行线被第三条直线所截,一组同旁内角的平分线互相垂直.
小颖根据命题画出图形并写出如下的已知条件.
已知:如图1,,直线分别交,于点,.的平分线与的平分线交于点.求证: .
(1)请补充要求证的结论,并写出证明过程;
(2)请从下列、两题中任选一题作答,我选择 题.
.在图1的基础上,分别作的平分线与的平分线交于点,得到图2,则的度数为 .
.如图3,,直线分别交,于点,.点在直线,之间,且在直线右侧,的平分线与的平分线交于点,则与满足的数量关系为 .
【解答】解:(1)结论:;
理由:如图1中,,
,
平分,平分,
,,
.
在中,,
,
.
故答案为.
(2).如图2中,由题意,,
平分,平分,
,
,
.如图3中,由题意,,,
平分,平分,
,,
,
故答案为或,,.
23.(2021春?长安区期末)如图1和图2,在三角形纸片中,点,分别在边,上,沿折叠,点落在点的位置.
(1)如图1,当点落在边上时,与之间的数量关系为
③ (只填序号),并说明理由;
①
②
③
(2)如图2,当点落在内部时,直接写出与,之间的数量关系.
【解答】解:(1)由题意得:.
.
故答案为:③.
(2),理由如下:
如图2,连接.
由题意知:.
,,
.
24.(2021春?长春期末)规律探索探索三角形的内(外角平分线形成的角的规律:
在三角形中,由三角形的内角平分线外角平分线所形成的角存在一定的规律.
规律1:三角形的两个内角的平分线形成的钝角等于加上第三个内角度数的一半;
规律2:三角形的两个外角的平分线形成的锐角等于减去与这两个外角不相邻的内角度数的一半.
问题呈现如图①,点是的内角平分线与的交点,点是的外角平分线与的交点,则,.
说明如下:
、是的角平分线,
,.
.①
.
.
请你仔细阅读理解上面的说理过程,完成下列问题:
(1)上述说理过程中步骤①的依据是
三角形内角和等于 .
(2)结合图①,写出说明的说理过程.
拓展延伸如图②,点是的内角平分线与的外角平分线的交点.若,则的大小为
度.
【解答】解:【问题呈现】
(1)证明过程中步骤(2)的依据是三角形内角和等于,
故答案为:三角形内角和等于;
(2)、是的外角平分线,
,,
,,
,
,
,
;
【拓展延伸】
平分,
,
平分,
,
,
,
,
,
,
即,
故答案为:25.
_21?????????è?????(www.21cnjy.com)_
三角形的初步知识——1.2+1.3定义与证明
一.选择题(共10小题)
1.(2021春?滑县期末)下列说法中,属于真命题的是
A.垂线最短
B.在同一平面内,过一点有且只有一条直线与已知直线垂直
C.相等的角一定是对顶角
D.两直线相交,邻补角相等
2.(2021春?峄城区期末)如图,在中,是边上的高,是的角平分线,若,,则的度数为
A.
B.
C.
D.
3.(2021春?莱州市期末)下列命题正确的是
A.若,则
B.若,则
C.若,则
D.若,则
4.(2021春?海口期末)如图,已知平分,交于点,过点作于点.若比大,则的度数是
A.
B.
C.
D.不能确定
5.(2021春?兴隆县期末)中,,,平分,点为上一点,于点,则的度数为
A.5
B.10
C.12
D.20
6.(2021春?福田区校级月考)如图,的高、相交于点,如果,那么的大小为
A.
B.
C.
D.
7.(2021春?碑林区校级期中)如图,,为的高线,角平分线,于点.当,时,的度数为
A.
B.
C.
D.
8.(2021春?高州市期末)如图,小明从一张三角形纸片的边上选取一点,将纸片沿着对折一次使得点落在处后,再将纸片沿着对折一次,使得点落在上的处,已知,,则原三角形的的度数为
A.
B.
C.
D.
9.(2020秋?章丘区期末)下面是投影屏上出示的解答题,需要回答横线上符号代表的内容.
如图,直线直线,在中,,顶点在上,顶点在上,且平分,若,求的度数.
解:,,
.
直线直线,
.
平分,
.
直线直线,
.
下列选项错误的是
A.代表
B.代表
C.在代表
D.代表
10.(2020秋?白银期末)如图,的角平分线、相交于,,,且于,下列结论:
①;②;
③平分;④.
其中正确的结论是
A.②③
B.①②④
C.①③④
D.①②③④
二.填空题(共8小题)
11.(2021春?滑县期末)命题“全等三角形的对应边相等”的逆命题是
;它是
.(填“真命题”或“假命题”
12.(2021春?高密市期末)有下列四个命题中,其中是真命题的是
.
.弧分为优弧和劣弧
.经过圆心的弦是直径
.若一个角的两边与另一个角的两边互相平行,则这两个角相等或互补
.三角形的一个外角大于三角形的每一个内角
13.(2021春?滦州市期末)已知:如图,是中边上的高,平分,若,,则 度.
14.(2021春?灵石县期末)如图,已知是的角平分线,,垂足为,交于,则下列命题:①,②,③,④,其中正确的是
.
15.(2021春?开州区期末)请将命题“坐标轴上的点至少有一个坐标为0”改写成“如果那么”的形式: .
16.(2021春?东坡区期末)如图中,、分别在边、上,将沿直线翻折后使点与点相重合.若,,则 .
17.(2021春?新都区期末)如图,将沿、翻折,使顶点、都落于点处,且线段、翻折后重合于,若,则 度.
18.(2021春?宽城区期末)将一副直角三角尺按如图所示的方式摆放,则的大小为
度.
三.解答题(共6小题)
19.(2021春?靖江市期末)如图,在四边形中,①,②,③.
(1)请你以其中两个为条件,第三个为结论,写出一个命题;
(2)判断这个命题是否为真命题,并说明理由.
20.(2021春?临西县期末)对于命题“相等的角是直角”,解决下列问题.
(1)指出命题的条件和结论,并改写成“如果那么”的形式;
(2)判断此命题是真命题还是假命题.
21.(2020春?博兴县期末)如图,有以下四个条件:①,②,③平分,④平分.
(1)若平分,,,求证:平分.
(2)除(1)外,请再选择四个条件中的三个作为题设,余下的一个作为结论,写出一个真命题,再给予证明.
22.(2019秋?太原期末)阅读下面内容,并解答问题.
在学行线的性质后,老师请学们证明命题:两条平行线被第三条直线所截,一组同旁内角的平分线互相垂直.
小颖根据命题画出图形并写出如下的已知条件.
已知:如图1,,直线分别交,于点,.的平分线与的平分线交于点.求证: .
(1)请补充要求证的结论,并写出证明过程;
(2)请从下列、两题中任选一题作答,我选择 题.
.在图1的基础上,分别作的平分线与的平分线交于点,得到图2,则的度数为 .
.如图3,,直线分别交,于点,.点在直线,之间,且在直线右侧,的平分线与的平分线交于点,则与满足的数量关系为 .
23.(2021春?长安区期末)如图1和图2,在三角形纸片中,点,分别在边,上,沿折叠,点落在点的位置.
(1)如图1,当点落在边上时,与之间的数量关系为
(只填序号),并说明理由;
①
②
③
(2)如图2,当点落在内部时,直接写出与,之间的数量关系.
24.(2021春?长春期末)规律探索探索三角形的内(外角平分线形成的角的规律:
在三角形中,由三角形的内角平分线外角平分线所形成的角存在一定的规律.
规律1:三角形的两个内角的平分线形成的钝角等于加上第三个内角度数的一半;
规律2:三角形的两个外角的平分线形成的锐角等于减去与这两个外角不相邻的内角度数的一半.
问题呈现如图①,点是的内角平分线与的交点,点是的外角平分线与的交点,则,.
说明如下:
、是的角平分线,
,.
.①
.
.
请你仔细阅读理解上面的说理过程,完成下列问题:
(1)上述说理过程中步骤①的依据是
.
(2)结合图①,写出说明的说理过程.
拓展延伸如图②,点是的内角平分线与的外角平分线的交点.若,则的大小为
度.
三角形的初步知识——1.2+1.3定义与证明
参考答案与试题解析
一.选择题(共10小题)
1.(2021春?滑县期末)下列说法中,属于真命题的是
A.垂线最短
B.在同一平面内,过一点有且只有一条直线与已知直线垂直
C.相等的角一定是对顶角
D.两直线相交,邻补角相等
【解答】解:、垂线段最短是真命题,垂线最短不是真命题,即不是真命题;
、在同一平面内,过一点有且只有一条直线与已知直线垂直,为真命题;
、对顶角一定相等,但相等的角不一定都是对顶角,相等的角一定是对顶角不正确,即不是真命题;
、两直线相交,同角的补角一定相等,邻补角相等不正确,即不是真命题.
故选:.
2.(2021春?峄城区期末)如图,在中,是边上的高,是的角平分线,若,,则的度数为
A.
B.
C.
D.
【解答】解:,,
.
是的角平分线,
.
.
是边上的高,
.
.
.
故选:.
3.(2021春?莱州市期末)下列命题正确的是
A.若,则
B.若,则
C.若,则
D.若,则
【解答】解:、若,则,原命题是假命题;
、若,,则,原命题是假命题;
、若,,则,原命题是假命题;
、若,则,是真命题;
故选:.
4.(2021春?海口期末)如图,已知平分,交于点,过点作于点.若比大,则的度数是
A.
B.
C.
D.不能确定
【解答】解:由题意知:.
平分,
.
又,
.
.
又,
.
.
.
,
.
,
.
故选:.
5.(2021春?兴隆县期末)中,,,平分,点为上一点,于点,则的度数为
A.5
B.10
C.12
D.20
【解答】解:,,
,
是的平分线,
,
,
又,
,
,
故选:.
6.(2021春?福田区校级月考)如图,的高、相交于点,如果,那么的大小为
A.
B.
C.
D.
【解答】解:如图,
、均为的高,
,
,
,
则.
故选:.
7.(2021春?碑林区校级期中)如图,,为的高线,角平分线,于点.当,时,的度数为
A.
B.
C.
D.
【解答】解:,
,
又,
,
又,
,
又平分,
,
,
故选:.
8.(2021春?高州市期末)如图,小明从一张三角形纸片的边上选取一点,将纸片沿着对折一次使得点落在处后,再将纸片沿着对折一次,使得点落在上的处,已知,,则原三角形的的度数为
A.
B.
C.
D.
【解答】解:如图,
由题意得:△,△.
,,.
.
.
又,
.
又,
.
.
.
.
故选:.
9.(2020秋?章丘区期末)下面是投影屏上出示的解答题,需要回答横线上符号代表的内容.
如图,直线直线,在中,,顶点在上,顶点在上,且平分,若,求的度数.
解:,,
.
直线直线,
.
平分,
.
直线直线,
.
下列选项错误的是
A.代表
B.代表
C.在代表
D.代表
【解答】解:,,
.
直线直线,
.
平分,
.
直线直线,
.
故选:.
10.(2020秋?白银期末)如图,的角平分线、相交于,,,且于,下列结论:
①;
②;
③平分;
④.
其中正确的结论是
A.②③
B.①②④
C.①③④
D.①②③④
【解答】解:,
,
平分,
,
,故①正确,
,
,
,
,
,
,
,
,,,
,故②正确,
假设平分,则,
,显然不符合题意,故③错误,
,,
,故④正确,
故选:.
二.填空题(共8小题)
11.(2021春?滑县期末)命题“全等三角形的对应边相等”的逆命题是
三边对应相等的三角形全等 ;它是
.(填“真命题”或“假命题”
【解答】解:命题“全等三角形的对应边相等”的逆命题是三边对应相等的三角形全等,逆命题是真命题;
故答案为:三边对应相等的三角形全等;真命题.
12.(2021春?高密市期末)有下列四个命题中,其中是真命题的是
, .
.弧分为优弧和劣弧
.经过圆心的弦是直径
.若一个角的两边与另一个角的两边互相平行,则这两个角相等或互补
.三角形的一个外角大于三角形的每一个内角
【解答】解:.弧分为优弧和劣弧,是假命题,弧分为优弧和劣弧,半圆.
.经过圆心的弦是直径,是真命题.
.若一个角的两边与另一个角的两边互相平行,则这两个角相等或互补,是真命题.
.三角形的一个外角大于三角形的每一个内角,是假命题.三角形的一个外角大于任何一个和他不相邻内角.
故答案为:,.
13.(2021春?滦州市期末)已知:如图,是中边上的高,平分,若,,则 14 度.
【解答】解:,,
.
是中边上的高,
.
平分,
.
,
,
.
故答案为:14.
14.(2021春?灵石县期末)如图,已知是的角平分线,,垂足为,交于,则下列命题:①,②,③,④,其中正确的是
①②③④ .
【解答】解:是的角平分线,
,
,
,
,,
,
,
,
,
,
故①②③④正确,
故答案为:①②③④
15.(2021春?开州区期末)请将命题“坐标轴上的点至少有一个坐标为0”改写成“如果那么”的形式: 如果一个点在坐标轴上,那么这个点至少有一个坐标为0 .
【解答】解:将命题“坐标轴上的点至少有一个坐标为0”改写成“如果那么”的形式:如果一个点在坐标轴上,那么这个点至少有一个坐标为0.
故答案为:如果一个点在坐标轴上,那么这个点至少有一个坐标为0.
16.(2021春?东坡区期末)如图中,、分别在边、上,将沿直线翻折后使点与点相重合.若,,则 .
【解答】解:由折叠可知:,,
,,
,
,
,
故答案为.
17.(2021春?新都区期末)如图,将沿、翻折,使顶点、都落于点处,且线段、翻折后重合于,若,则 63 度.
【解答】解:连接、,如图所示:
由折叠的性质得:,
,,
又由折叠的性质得:,,
,,
,,,
,
,
,
,
故答案为:63.
18.(2021春?宽城区期末)将一副直角三角尺按如图所示的方式摆放,则的大小为
75 度.
【解答】解:,
故答案为:75.
三.解答题(共6小题)
19.(2021春?靖江市期末)如图,在四边形中,①,②,③.
(1)请你以其中两个为条件,第三个为结论,写出一个命题;
(2)判断这个命题是否为真命题,并说明理由.
【解答】解:(1)如果,,那么;
(2)这个命题是真命题,
证明:,
,
,
,
.
20.(2021春?临西县期末)对于命题“相等的角是直角”,解决下列问题.
(1)指出命题的条件和结论,并改写成“如果那么”的形式;
(2)判断此命题是真命题还是假命题.
【解答】解:(1)命题“相等的角是直角”的条件是两个角是相等;结论是这两个角是直角,
改写成“如果那么”的形式为:如果两个角相等,那么这两个角都是直角;
(2)“相等的角是直角”是假命题.
21.(2020春?博兴县期末)如图,有以下四个条件:①,②,③平分,④平分.
(1)若平分,,,求证:平分.
(2)除(1)外,请再选择四个条件中的三个作为题设,余下的一个作为结论,写出一个真命题,再给予证明.
【解答】(1)证明:平分,
,
,
,,
,
,
,即平分.
(2)解:如果平分,,,那么平分.
证明:平分,
,
,
,,
,
,
,即平分.
22.(2019秋?太原期末)阅读下面内容,并解答问题.
在学行线的性质后,老师请学们证明命题:两条平行线被第三条直线所截,一组同旁内角的平分线互相垂直.
小颖根据命题画出图形并写出如下的已知条件.
已知:如图1,,直线分别交,于点,.的平分线与的平分线交于点.求证: .
(1)请补充要求证的结论,并写出证明过程;
(2)请从下列、两题中任选一题作答,我选择 题.
.在图1的基础上,分别作的平分线与的平分线交于点,得到图2,则的度数为 .
.如图3,,直线分别交,于点,.点在直线,之间,且在直线右侧,的平分线与的平分线交于点,则与满足的数量关系为 .
【解答】解:(1)结论:;
理由:如图1中,,
,
平分,平分,
,,
.
在中,,
,
.
故答案为.
(2).如图2中,由题意,,
平分,平分,
,
,
.如图3中,由题意,,,
平分,平分,
,,
,
故答案为或,,.
23.(2021春?长安区期末)如图1和图2,在三角形纸片中,点,分别在边,上,沿折叠,点落在点的位置.
(1)如图1,当点落在边上时,与之间的数量关系为
③ (只填序号),并说明理由;
①
②
③
(2)如图2,当点落在内部时,直接写出与,之间的数量关系.
【解答】解:(1)由题意得:.
.
故答案为:③.
(2),理由如下:
如图2,连接.
由题意知:.
,,
.
24.(2021春?长春期末)规律探索探索三角形的内(外角平分线形成的角的规律:
在三角形中,由三角形的内角平分线外角平分线所形成的角存在一定的规律.
规律1:三角形的两个内角的平分线形成的钝角等于加上第三个内角度数的一半;
规律2:三角形的两个外角的平分线形成的锐角等于减去与这两个外角不相邻的内角度数的一半.
问题呈现如图①,点是的内角平分线与的交点,点是的外角平分线与的交点,则,.
说明如下:
、是的角平分线,
,.
.①
.
.
请你仔细阅读理解上面的说理过程,完成下列问题:
(1)上述说理过程中步骤①的依据是
三角形内角和等于 .
(2)结合图①,写出说明的说理过程.
拓展延伸如图②,点是的内角平分线与的外角平分线的交点.若,则的大小为
度.
【解答】解:【问题呈现】
(1)证明过程中步骤(2)的依据是三角形内角和等于,
故答案为:三角形内角和等于;
(2)、是的外角平分线,
,,
,,
,
,
,
;
【拓展延伸】
平分,
,
平分,
,
,
,
,
,
,
即,
故答案为:25.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
