1.6 尺规作图 同步练习（含解析）

中小学教育资源及组卷应用平台
三角形的初步知识——1.6尺规作图
一．选择题（共10小题）
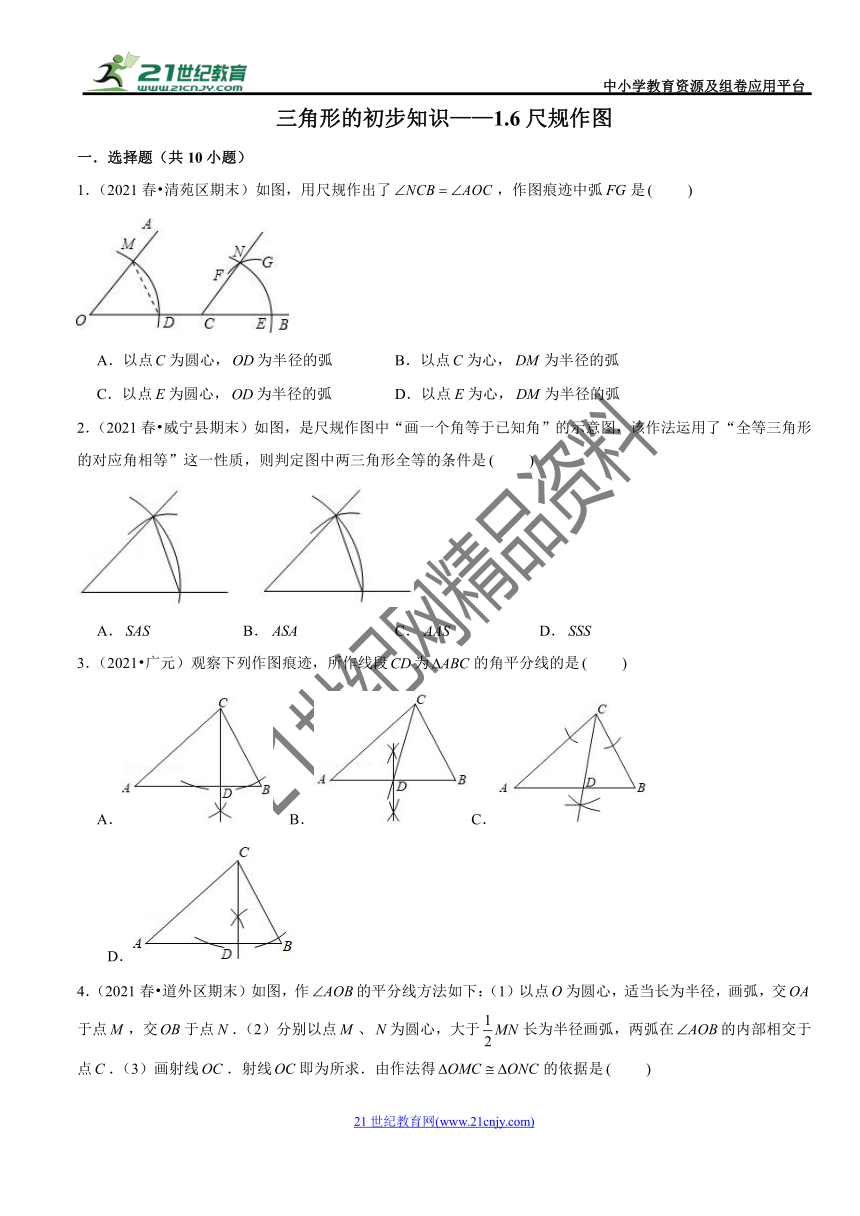
1．（2021春?清苑区期末）如图，用尺规作出了，作图痕迹中弧是　　
A．以点为圆心，为半径的弧 B．以点为心，为半径的弧
C．以点为圆心，为半径的弧 D．以点为心，为半径的弧
2．（2021春?威宁县期末）如图，是尺规作图中“画一个角等于已知角”的示意图，该作法运用了“全等三角形的对应角相等”这一性质，则判定图中两三角形全等的条件是　　
A． B． C． D．
3．（2021?广元）观察下列作图痕迹，所作线段为的角平分线的是　　
A． B． C． D．
4．（2021春?道外区期末）如图，作的平分线方法如下：（1）以点为圆心，适当长为半径，画弧，交于点，交于点．（2）分别以点、为圆心，大于长为半径画弧，两弧在的内部相交于点．（3）画射线．射线即为所求．由作法得的依据是　　
A． B． C． D．
5．（2020秋?巩义市期末）已知锐角，如图：
（1）在射线上取一点，以点为圆心，长为半径作弧，交射线于点，连接；
（2）分别以点，为圆心，长为半径作弧，两弧交于点，连接，；
（3）作射线交于点．
根据以上作图过程及所作图形，有如下结论：①；②；③；④．
其中正确的有　　
A．①②③④ B．②③④ C．③④ D．③
6．（2021?通辽）如图，在中，，根据尺规作图的痕迹，判断以下结论错误的是　　
A． B． C． D．
7．（2021?福田区一模）如图，依据尺规作图的痕迹，计算　　
A． B． C． D．
8．（2020秋?滦南县期末）如图，在中．，，按以下步骤作图：①以点为圆心，小于长为半径画弧，分别交，于点、；②分别以点、为圆心，大于长为半径画弧，两弧交于点；③作射线，交边于点，则的度数为　　
A． B． C． D．
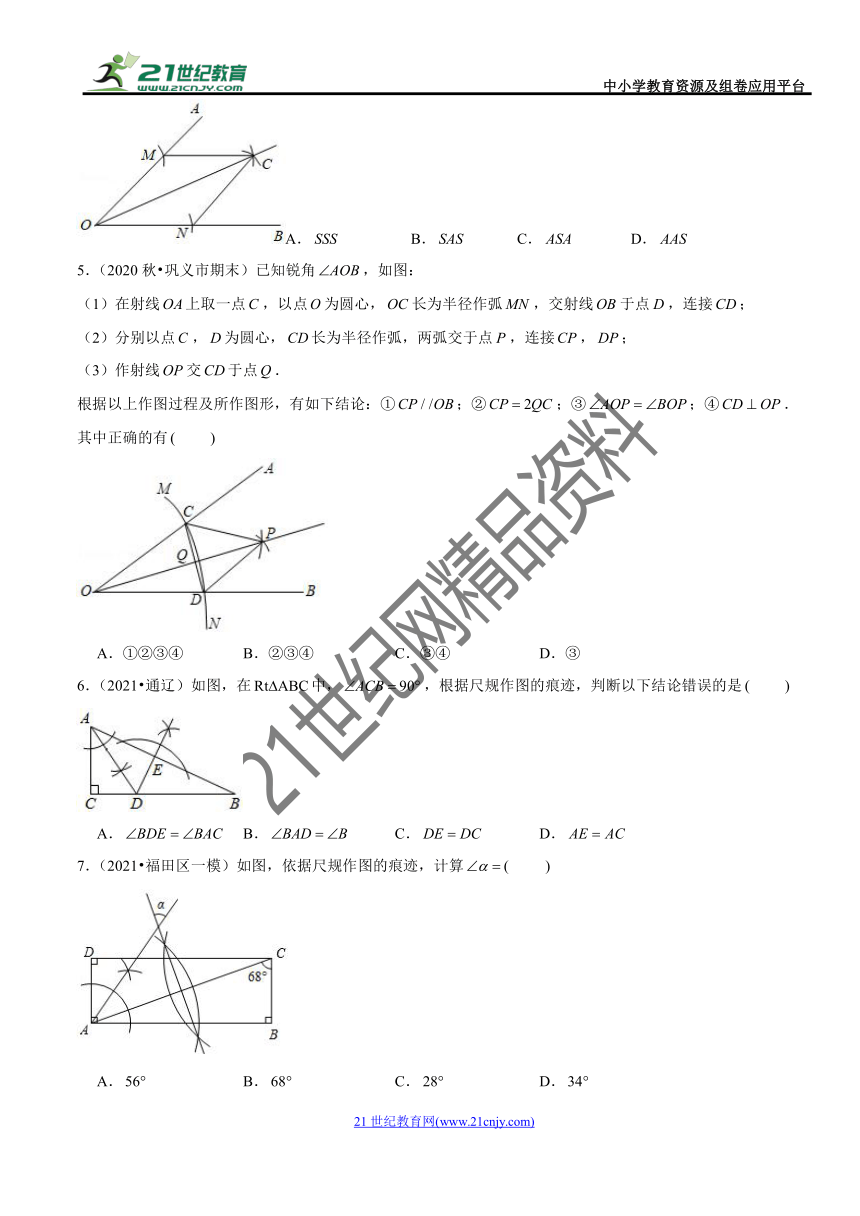
9．（2018?安顺）已知，用尺规作图的方法在上确定一点，使，则符合要求的作图痕迹是　　
A． B．
C． D．
10．（2020?衢州）过直线外一点作直线的平行线，下列尺规作图中错误的是　　
A． B．
C． D．
二．填空题（共8小题）
11．（2018秋?延庆区期中）如图，小敏做了一个角平分仪，其中，，将仪器上的点与的顶点重合，调整和，使它们分别落在角的两边上，过点，画一条射线，就是的平分线，此角平分仪的画图原理是：根据仪器结构，可得，这样就有，请你用文字语言叙述这两个三角形全等的依据是　　．
12．（2021春?新都区期末）如图，在中，，利用尺规在，上分别截取；分别以点，为圆心，以大于的长为半径作弧，两弧在内部交于点；作射线交于点．若，点为线段上的一动点，则的最小值是 　　．
13．（2021?抚顺）如图，中，，以点为圆心，长为半径画弧，交于点，分别以点，为圆心，大于的长为半径画弧两弧相交于点，作射线，交于点，于点．若，则的长为 　　．
14．（2019秋?襄汾县期末）如图，在，，，按以下步骤作图：
①以点为圆心，小于的长为半径．画弧，分别交、于点、；
②分别以点、为圆心，大于的长为半径画弧，两弧相交于点；
③作射线，交边于点，则的度数为　 　．
15．（2020?葫芦岛）如图，在中，，，，以为圆心，以适当的长为半径作弧，交于点，交于点．分别以，为圆心，以大于的长为半径作弧，两弧在的内部相交于点，作射线，交于点，点在边上，，连接，则的周长为　　．
16．（2020春?青神县期中）如图，在中，，以点为圆心，长为半径作弧，交于点，交于点；再分别以点和点为圆心，大于的长为半径作弧，两弧相交于点，作射线交于点．若以点为圆心，长为半径画弧，这段弧恰好经过、两点，则此时的度数是　　．
17．（2021?台安县模拟）如图，直线，直线分别与，相交于点，．小宇同学利用以下步骤作图：
①以点为圆心，适当长为半径作弧交射线于点，交线段于点；
②以点为圆心，适当长为半径画弧；然后再以点为圆心，同样长为半径画弧．前后两弧在内交于点；
③作射线，交于点，
若，，则线段的长为　　．
18．（2021春?海阳市期末）如图的尺规作图是，分别以线段的端点为圆心，以小于长为半径画弧，分别交射线与线段于点，，再以点为圆心，以长为半径画弧，交前面的弧于点，画射线分别以点，为圆心，大于长为半径画弧，两弧交于点，画射线．若，则的度数为 　　．
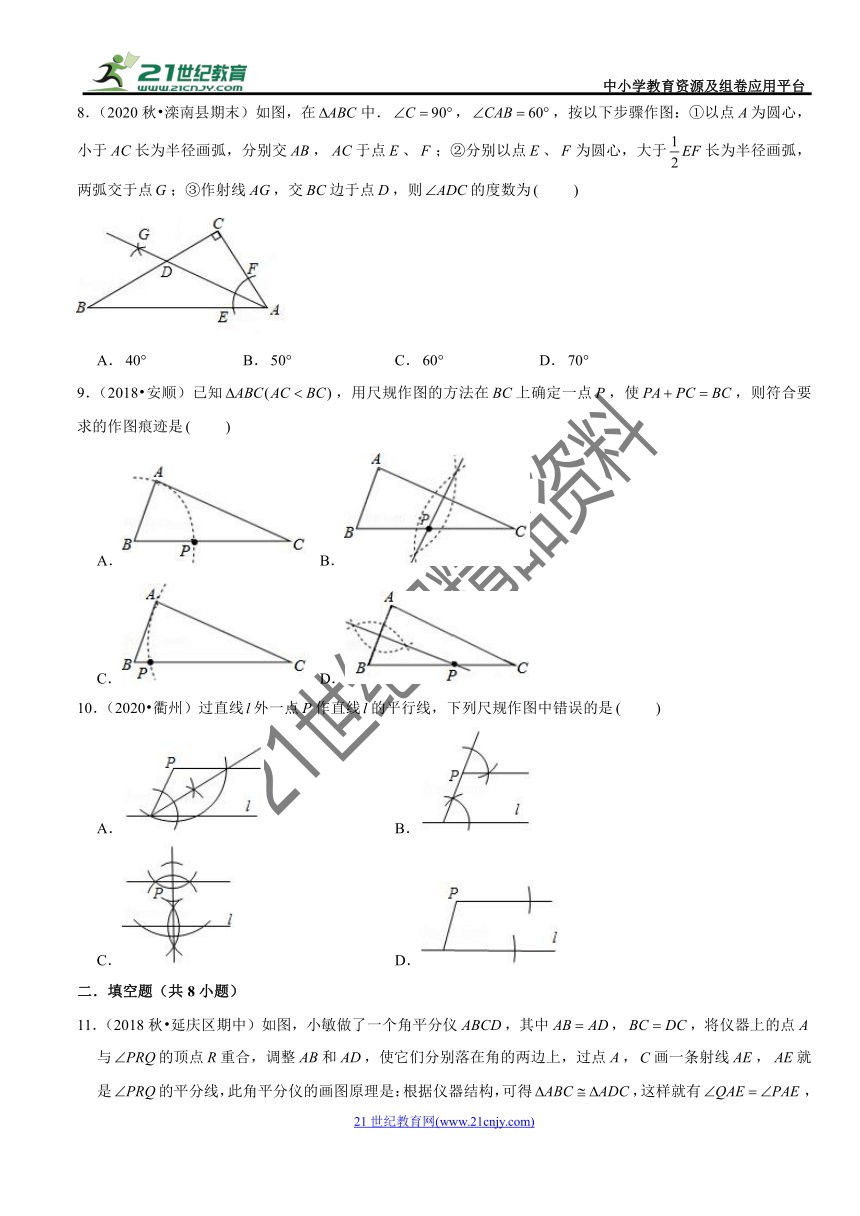
三．解答题（共6小题）
19．（2021春?莱州市期末）尺规作图题．已知：，．求作：，使．要求：不写作法，保留作图痕迹；标注字母，，．
20．（2021春?长安区期末）尺规作图（保留作图痕迹，不写作法）
如图，直线表示一条公路，、表示两所大学，要在公路旁修建一个车站，使车站到两所大学的距离相等．
（1）请用尺规在图上找出点；（2）请说明你作图的依据．
21．（2021春?讷河市期末）（1）请你根据图1回答下列问题：
①若，可以得到哪两条线段平行？
②在①的结论下，如果，又能得到哪两条线段平行？
（2）请你在图2中按下面的要求画图（画图工具和方法不限）：过点画于，过点画交于，在线段上任取一点，以为顶点，为一边画，使，的另一边与线段交于点．
（3）请你根据（2）中画图时给出的条件，猜想与的位置关系，并给予证明．
22．（2019秋?青龙县期末）如图，校园有两条路、，在交叉路口附近有两块宣传牌、，学校准备在这里安装一盏路灯，要求灯柱的位置离两块宣传牌一样远，并且到两条路的距离也一样远，请你帮助画出灯柱的位置，简要说明理由．
23．（2021春?九江期末）如图1，在一纸张内没有交点的两条直线，，如何确定出这两条直线所成的角的度数？聪明的小文是这么做的：作与直线平行，则直线与的夹角度数就是直线，所成角的度数．
（1）这种做法的理由是 　　；
（2）小文在此基础上又进行了如下操作（如图：①以为圆心，任意长为半径画圆弧，分别交直线，于点，；②连结并延长交直线于点，请写出图中所有与相等的角；
（3）请在图2纸张内作出“直线，所成的跑到纸张外面去的角”的角平分线，只要求作出图形，并保留作图痕迹．
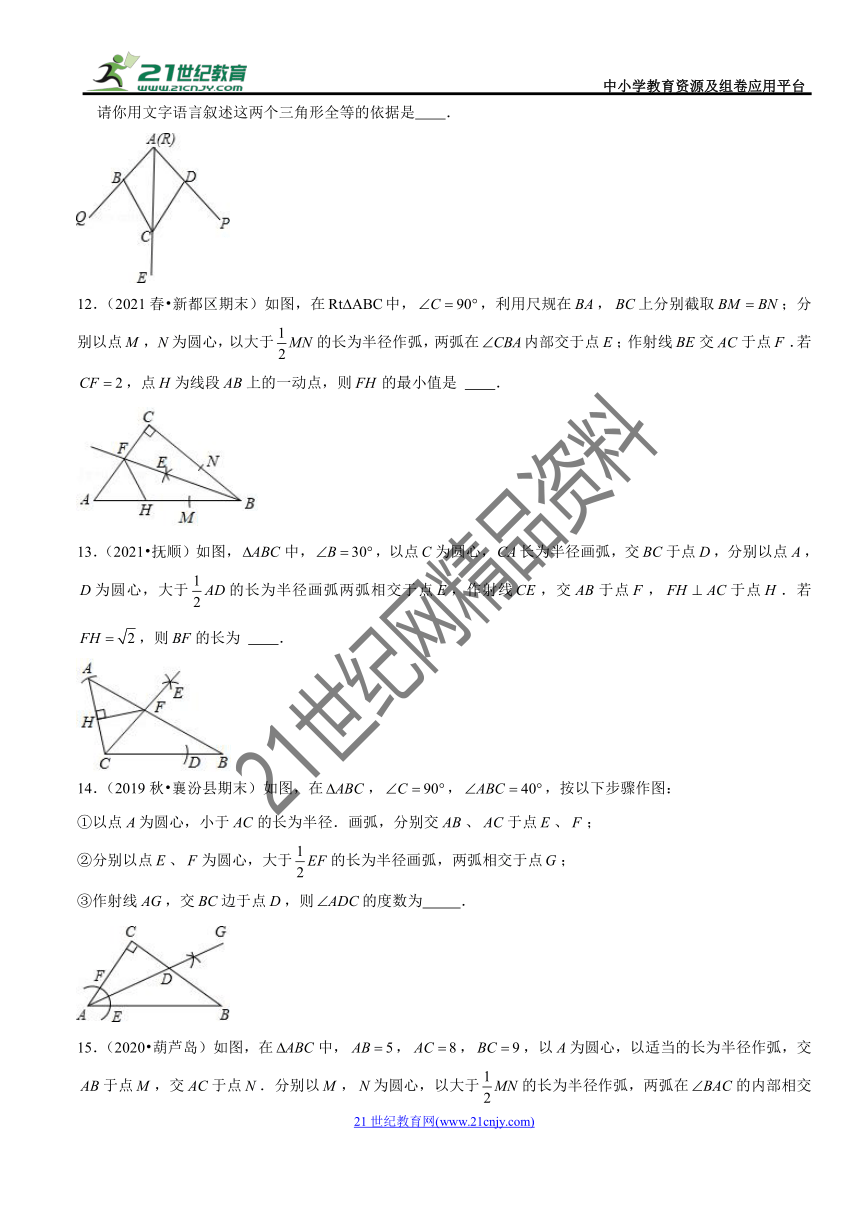
24．（2021?衢州）如图，在的网格中，的三个顶点都在格点上．
（1）在图1中画出，使与全等，顶点在格点上．
（2）在图2中过点画出平分面积的直线．
三角形的初步知识——1.6尺规作图
参考答案与试题解析
一．选择题（共10小题）
1．（2021春?清苑区期末）如图，用尺规作出了，作图痕迹中弧是　　
A．以点为圆心，为半径的弧 B．以点为心，为半径的弧
C．以点为圆心，为半径的弧 D．以点为心，为半径的弧
【解答】解：根据作一个角等于已知角可得弧是以点为圆心，为半径的弧．
故选：．
2．（2021春?威宁县期末）如图，是尺规作图中“画一个角等于已知角”的示意图，该作法运用了“全等三角形的对应角相等”这一性质，则判定图中两三角形全等的条件是　　
A． B． C． D．
【解答】解：如图，由作图可知，，．
在和中，
，
，
故选：．
3．（2021?广元）观察下列作图痕迹，所作线段为的角平分线的是　　
A．
B．
C．
D．
【解答】解：根据基本作图，、选项中为过点作的垂线，选项作的垂直平分线得到边上的中线，选项作平分．
故选：．
4．（2021春?道外区期末）如图，作的平分线方法如下：（1）以点为圆心，适当长为半径，画弧，交于点，交于点．（2）分别以点、为圆心，大于长为半径画弧，两弧在的内部相交于点．（3）画射线．射线即为所求．由作法得的依据是　　
A． B． C． D．
【解答】解：由作法得，，
而为公共边，
所以根据“”可判断．
故选：．
5．（2020秋?巩义市期末）已知锐角，如图：
（1）在射线上取一点，以点为圆心，长为半径作弧，交射线于点，连接；
（2）分别以点，为圆心，长为半径作弧，两弧交于点，连接，；
（3）作射线交于点．
根据以上作图过程及所作图形，有如下结论：①；②；③；④．
其中正确的有　　
A．①②③④ B．②③④ C．③④ D．③
【解答】解：由作图可知，，，
在和中，
，
，
，故③正确，
由作图可知，，
是等边三角形，
，
，，
，故④正确，
，
，故②正确，
显然不是，
与显然不平行，
故选：．
6．（2021?通辽）如图，在中，，根据尺规作图的痕迹，判断以下结论错误的是　　
A． B． C． D．
【解答】解：根据尺规作图的痕迹可得，，是的平分线，
，
，，
，
在和中，
，
，
，
不是的垂直平分线，故不能证明，
综上所述：，，不符合题意，符合题意，
故选：．
7．（2021?福田区一模）如图，依据尺规作图的痕迹，计算　　
A． B． C． D．
【解答】解：四边形是矩形，
，
．
由作法可知，是的平分线，
．
由作法可知，是线段的垂直平分线，
，
，
．
故选：．
8．（2020秋?滦南县期末）如图，在中．，，按以下步骤作图：①以点为圆心，小于长为半径画弧，分别交，于点、；②分别以点、为圆心，大于长为半径画弧，两弧交于点；③作射线，交边于点，则的度数为　　
A． B． C． D．
【解答】解：在中，，，
根据作图过程可知：
是的平分线，
，
，
．
故选：．
9．（2018?安顺）已知，用尺规作图的方法在上确定一点，使，则符合要求的作图痕迹是
　　
A．
B．
C．
D．
【解答】解：、如图所示：此时，则无法得出，故不能得出，故此选项错误；
、如图所示：此时，则无法得出，故不能得出，故此选项错误；
、如图所示：此时，则无法得出，故不能得出，故此选项错误；
、如图所示：此时，故能得出，故此选项正确；
故选：．
10．（2020?衢州）过直线外一点作直线的平行线，下列尺规作图中错误的是　　
A． B．
C． D．
【解答】解：、本选项作了角的平分线与等腰三角形，能得到一组内错角相等，从而可证两直线平行，故本选项不符合题意．
、本选项作了一个角等于已知角，根据同位角相等两直线平行，能判断是过点且与直线的平行直线，本选项不符合题意．
、由作图可知，垂直于同一条直线的两条直线平行，本选项不符合题意．
、作图只截取了两条线段相等，而无法保证两直线平行的位置关系，本选项符合题意．
故选：．
二．填空题（共8小题）
11．（2018秋?延庆区期中）如图，小敏做了一个角平分仪，其中，，将仪器上的点与的顶点重合，调整和，使它们分别落在角的两边上，过点，画一条射线，就是的平分线，此角平分仪的画图原理是：根据仪器结构，可得，这样就有，请你用文字语言叙述这两个三角形全等的依据是　　．
【解答】解：在和中，
，
，
，
即．
故答案为：．
12．（2021春?新都区期末）如图，在中，，利用尺规在，上分别截取；分别以点，为圆心，以大于的长为半径作弧，两弧在内部交于点；作射线交于点．若，点为线段上的一动点，则的最小值是 　2　．
【解答】解：如图，过点作于．
由作图可知，平分，
，，
，
根据垂线段最短可知，的最小值为2，
故答案为：2．
13．（2021?抚顺）如图，中，，以点为圆心，长为半径画弧，交于点，分别以点，为圆心，大于的长为半径画弧两弧相交于点，作射线，交于点，于点．若，则的长为 　　．
【解答】解：过作于，
由作图知，是的角平分线，
于点．，
，
，．
，
故答案为：．
14．（2019秋?襄汾县期末）如图，在，，，按以下步骤作图：
①以点为圆心，小于的长为半径．画弧，分别交、于点、；
②分别以点、为圆心，大于的长为半径画弧，两弧相交于点；
③作射线，交边于点，则的度数为　　．
【解答】解：解法一：连接．
点、是以点为圆心，小于的长为半径画弧，分别与、的交点，
；
是等腰三角形；
又分别以点、为圆心，大于的长为半径画弧，两弧相交于点；
是线段的垂直平分线，
平分，
，
；
在中，，，
（直角三角形中的两个锐角互余）；
解法二：根据已知条件中的作图步骤知，是的平分线，
，
；
在中，，，
（直角三角形中的两个锐角互余）；
故答案是：．
15．（2020?葫芦岛）如图，在中，，，，以为圆心，以适当的长为半径作弧，交于点，交于点．分别以，为圆心，以大于的长为半径作弧，两弧在的内部相交于点，作射线，交于点，点在边上，，连接，则的周长为　12　．
【解答】解：，，，
，
由作图方法可得：平分，
，
在和中
，
，
，
的周长为：．
故答案为：12．
16．（2020春?青神县期中）如图，在中，，以点为圆心，长为半径作弧，交于点，交于点；再分别以点和点为圆心，大于的长为半径作弧，两弧相交于点，作射线交于点．若以点为圆心，长为半径画弧，这段弧恰好经过、两点，则此时的度数是　　．
【解答】解：连接，如图，设，，
由作法得，垂直平分，
以点为圆心，长为半径画弧，这段弧恰好经过、两点，
，
，
，
，
，
，
，
，即，
，
，
．
故答案为．
17．（2021?台安县模拟）如图，直线，直线分别与，相交于点，．小宇同学利用以下步骤作图：
①以点为圆心，适当长为半径作弧交射线于点，交线段于点；
②以点为圆心，适当长为半径画弧；然后再以点为圆心，同样长为半径画弧．前后两弧在内交于点；
③作射线，交于点，
若，，则线段的长为　2　．
【解答】解：如图，过作于，
，
，
由题意得：平分，
，
，
，
又，
，
中，，
故答案为：2．
18．（2021春?海阳市期末）如图的尺规作图是，分别以线段的端点为圆心，以小于长为半径画弧，分别交射线与线段于点，，再以点为圆心，以长为半径画弧，交前面的弧于点，画射线分别以点，为圆心，大于长为半径画弧，两弧交于点，画射线．若，则的度数为 　　．
【解答】解：根据作图过程可知：，，
因为，
所以
故答案为：．
三．解答题（共6小题）
19．（2021春?莱州市期末）尺规作图题．已知：，．求作：，使．要求：不写作法，保留作图痕迹；标注字母，，．
【解答】解：如下图所示：．
所以即为所求．
20．（2021春?长安区期末）尺规作图（保留作图痕迹，不写作法）
如图，直线表示一条公路，、表示两所大学，要在公路旁修建一个车站，使车站到两所大学的距离相等．
（1）请用尺规在图上找出点；
（2）请说明你作图的依据．
【解答】解：（1）如图，点即为所求．
（2）垂直平分线段，
（线段的垂直平分线上的点到线段的两个端点的距离相等）．
21．（2021春?讷河市期末）（1）请你根据图1回答下列问题：
①若，可以得到哪两条线段平行？
②在①的结论下，如果，又能得到哪两条线段平行？
（2）请你在图2中按下面的要求画图（画图工具和方法不限）：过点画于，过点画交于，在线段上任取一点，以为顶点，为一边画，使，的另一边与线段交于点．
（3）请你根据（2）中画图时给出的条件，猜想与的位置关系，并给予证明．
【解答】解：（1）①，
．
②，
，
，
，
．
（2）如图，
（3）结论：．
理由：，
．
又，
，
，
于，
．
，
，
．
22．（2019秋?青龙县期末）如图，校园有两条路、，在交叉路口附近有两块宣传牌、，学校准备在这里安装一盏路灯，要求灯柱的位置离两块宣传牌一样远，并且到两条路的距离也一样远，请你帮助画出灯柱的位置，简要说明理由．
【解答】解：灯柱的位置在的平分线和的垂直平分线的交点上．
在的平分线上，
到两条路的距离一样远；
在线段的垂直平分线上，
到和的距离相等，符合题意．
23．（2021春?九江期末）如图1，在一纸张内没有交点的两条直线，，如何确定出这两条直线所成的角的度数？聪明的小文是这么做的：作与直线平行，则直线与的夹角度数就是直线，所成角的度数．
（1）这种做法的理由是 　两直线平行同位角相等　；
（2）小文在此基础上又进行了如下操作（如图：①以为圆心，任意长为半径画圆弧，分别交直线，于点，；②连结并延长交直线于点，请写出图中所有与相等的角；
（3）请在图2纸张内作出“直线，所成的跑到纸张外面去的角”的角平分线，只要求作出图形，并保留作图痕迹．
【解答】解：（1）如图1，作出直线、所成的角，
，
（两直线平行同位角相等），
即直线与的夹角度数，即直线，所成角的度数．
故答案为：两直线平行同位角相等
（2）如图2，，理由是：
，
，
，
，
，
，
．
（3）如图1中，射线即为所求．
24．（2021?衢州）如图，在的网格中，的三个顶点都在格点上．
（1）在图1中画出，使与全等，顶点在格点上．
（2）在图2中过点画出平分面积的直线．
【解答】解：（1）如图1中，即为所求．
（2）如图2中，直线即为所求．
_21?????????è?????(www.21cnjy.com)_