1.5 全等三角形的判定 (1) 同步练习(含解析)
文档属性
| 名称 | 1.5 全等三角形的判定 (1) 同步练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-16 21:24:22 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
三角形的初步认识——1.5全等三角形的判定
一.选择题(共10小题)
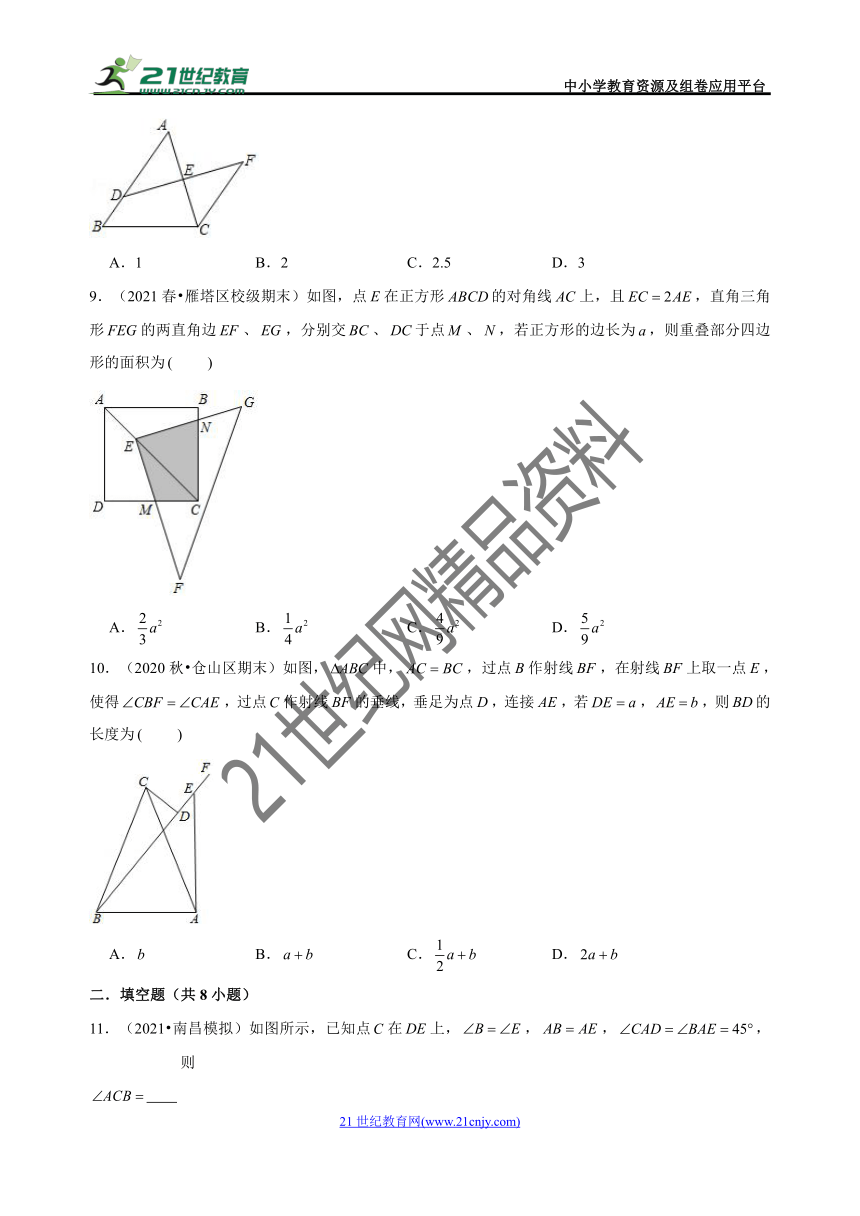
1.(2021春 祥符区期末)如图,已知,下列所给条件不一定能使与全等的是
A. B. C. D.
2.(2021春 锦江区校级期末)如图,已知三条边、三个角,则甲、乙两个三角形中,与全等的图形是
A.甲 B.乙 C.甲和乙 D.都不是
3.(2021春 历城区期末)如图,用纸板挡住了三角形的一部分,小明根据所学知识很快就重新画出了一个与原来完全一样的三角形,他的依据是
A. B. C. D.
4.(2021春 九龙坡区校级期末)如图,、、、四点在同一直线上,在和中,,,添加下列条件,仍不能证明的是
A. B. C. D.
5.(2021春 砀山县期末)一块三角形玻璃样板不慎被张字同学碰破,成了四片完整碎片(如图所示),聪明的他经过仔细地考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板,你认为下列四个答案中考虑最全面的是
A.带1,2或2,3去就可以了 B.带1,4或3,4去就可以了
C.带1,4或2,4或3,4去均可 D.带其中的任意两块去都可以
6.(2020秋 射阳县期末)工人师傅常用角尺平分一个任意角.作法如下:如图所示,是一个任意角,在边,上分别取,移动角尺,使角尺两边相同的刻度分别与,重合,过角尺顶点的射线即是的平分线.这种作法的道理是
A. B. C. D.
7.(2021春 乐平市期末)如图,已知,,点、、、四点在同一直线上.要利用“”来判定,下列四个条件:①;②;③;④.可以利用的是
A.①② B.②④ C.②③ D.①④
8.(2021春 莲湖区期末)如图,是的边的中点,过点作,过点作直线交于,交于,若,,则的长为
A.1 B.2 C.2.5 D.3
9.(2021春 雁塔区校级期末)如图,点在正方形的对角线上,且,直角三角形的两直角边、,分别交、于点、,若正方形的边长为,则重叠部分四边形的面积为
A. B. C. D.
10.(2020秋 仓山区期末)如图,中,,过点作射线,在射线上取一点,使得,过点作射线的垂线,垂足为点,连接,若,,则的长度为
A. B. C. D.
二.填空题(共8小题)
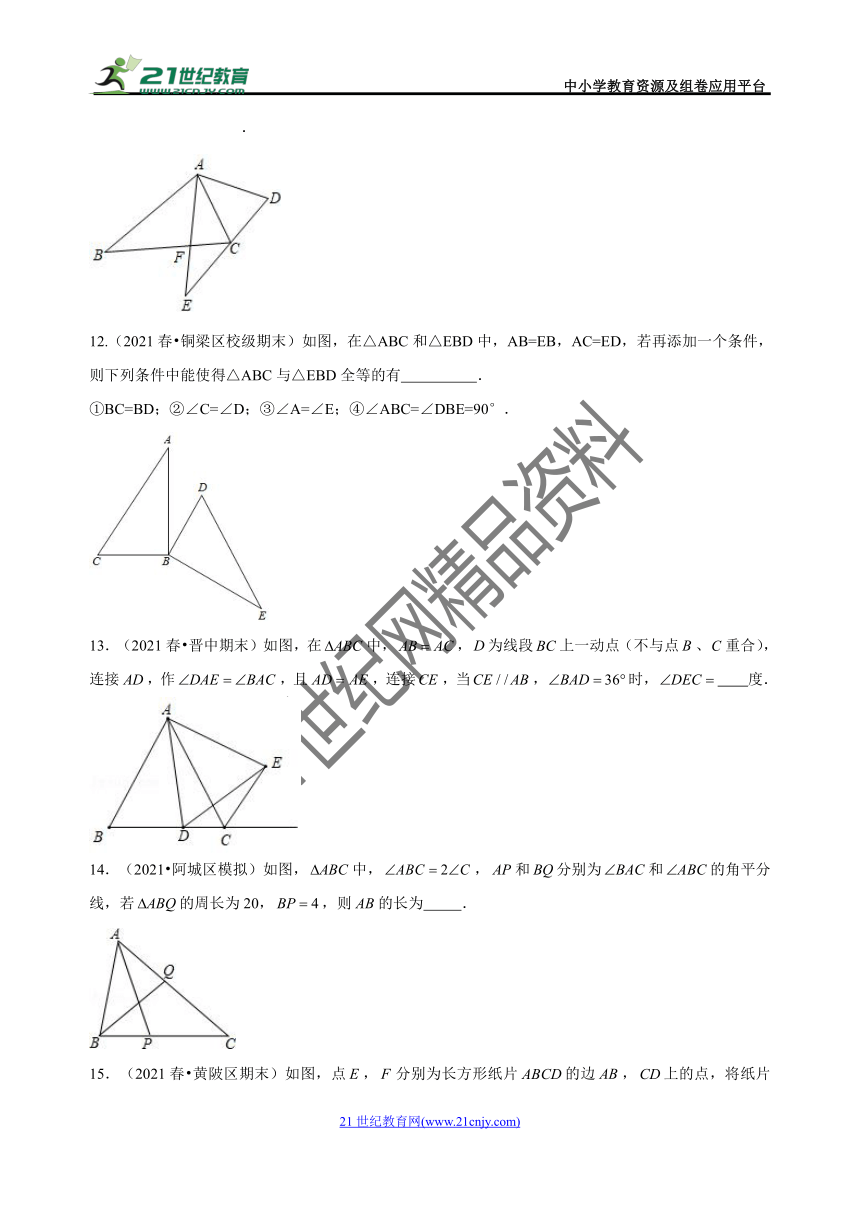
11.(2021 南昌模拟)如图所示,已知点在上,,,,则
.
12.(2021春 铜梁区校级期末)如图,在△ABC和△EBD中,AB=EB,AC=ED,若再添加一个条件,则下列条件中能使得△ABC与△EBD全等的有 .
①BC=BD;②∠C=∠D;③∠A=∠E;④∠ABC=∠DBE=90°.
13.(2021春 晋中期末)如图,在中,,为线段上一动点(不与点、重合),连接,作,且,连接,当,时, 度.
14.(2021 阿城区模拟)如图,中,,和分别为和的角平分线,若的周长为20,,则的长为 .
15.(2021春 黄陂区期末)如图,点,分别为长方形纸片的边,上的点,将纸片沿翻折,点,分别落在点,处.下列结论一定正确的有 (填序号即可).
①;
②;
③;
④若的度数比的2倍还多,则的度数为.
16.(2021春 和平区期末)如图,在中,,,,与相交于点,连接并延长交于点,的平分线交的延长线于点,连接,则下列结论:
①;②;③;④;
⑤.其中正确的是 .(只填写序号)
17.(2021春 龙岗区期末)如图,在中,为的中点,是上一点,连接并延长交于,,且,,则的长度为 .
18.(2021春 历下区期末)如图,AB=4cm,AC=BD=3cm,∠CAB=∠DBA,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,设运动时间为t(s),则当△ACP与△BPQ全等时,点Q的运动速度为
三.解答题(共6小题)
19.(2021 泰兴市模拟)如图,点、分别在、上,、相交于点, .求证:.
在“①;②;③”这三个条件中选择两个填入上面的横线上
(只要填写序号),并完成解答.
20.(2021 广东二模)如图,,,,求证:.
21.(2021 南岗区模拟)已知:点,在上,,,.
(1)如图1,求证:;
(2)如图2,连接,,,,在不添加任何辅助线的情况下,请直接写出图2中的四组平行线.
22.(2021 南岗区模拟)已知:在和中,,,其中.
(1)如图1,求证:;
(2)如图2,,分别交,于点,,交于点,在不添加任何辅助线的情况下,请直接写出图2中的四对全等三角形.
23.(2021 镇海区模拟)如图,已知和均是直角三角形,,,于点.求证:;
24.(2020秋 宜宾期末)在中,,,,点在上,且,过点作射线与在同侧),若动点从点出发,沿射线匀速运动,运动速度为,设点运动时间为秒.连接、.
(1)如图①,当时,求证:;
(2)如图②,当于点时,求此时的值.
三角形的初步认识——1.5全等三角形的判定
参考答案与试题解析
一.选择题(共10小题)
1.(2021春 祥符区期末)如图,已知,下列所给条件不一定能使与全等的是
A. B. C. D.
【解答】解:由图可得,
,
又,
当时,,故选项不符合题意;
当时,和不一定全等,故选项符合题意;
当时,,故选项不符合题意;
当时,,故选项不符合题意;
故选:.
2.(2021春 锦江区校级期末)如图,已知三条边、三个角,则甲、乙两个三角形中,与全等的图形是
A.甲 B.乙 C.甲和乙 D.都不是
【解答】解:甲三角形夹边的两角分别与已知三角形对应相等,故甲与全等;
乙三角形内角及所对边与对应相等且均有内角,可根据判定乙与全等;
则与全等的有乙和甲,
故选:.
3.(2021春 历城区期末)如图,用纸板挡住了三角形的一部分,小明根据所学知识很快就重新画出了一个与原来完全一样的三角形,他的依据是
A. B. C. D.
【解答】解:如图,
只要量出的长和和的度数,再画出一个三角形,使,,即可,
故选:.
4.(2021春 九龙坡区校级期末)如图,、、、四点在同一直线上,在和中,,,添加下列条件,仍不能证明的是
A. B. C. D.
【解答】解:,,
若添加,则两个三角形满足,
不一定全对,符合题意;
若添加:,则两个三角形全等,不符合题意;
若添加,则,则两个三角形全等,不符合题意;
若添加,则,则两个三角形全等,不符合题意;
故选:.
5.(2021春 砀山县期末)一块三角形玻璃样板不慎被张字同学碰破,成了四片完整碎片(如图所示),聪明的他经过仔细地考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板,你认为下列四个答案中考虑最全面的是
A.带1,2或2,3去就可以了 B.带1,4或3,4去就可以了
C.带1,4或2,4或3,4去均可 D.带其中的任意两块去都可以
【解答】解:带3、4可以用“角边角”确定三角形,
带1、4可以用“角边角”确定三角形,
带2、4可以延长还原出原三角形,
故选:.
6.(2020秋 射阳县期末)工人师傅常用角尺平分一个任意角.作法如下:如图所示,是一个任意角,在边,上分别取,移动角尺,使角尺两边相同的刻度分别与,重合,过角尺顶点的射线即是的平分线.这种作法的道理是
A. B. C. D.
【解答】解:由图可知,,又,为公共边,
,
,
即即是的平分线.
故选:.
7.(2021春 乐平市期末)如图,已知,,点、、、四点在同一直线上.要利用“”来判定,下列四个条件:①;②;③;④.可以利用的是
A.①② B.②④ C.②③ D.①④
【解答】解:,
,即,
,
当时,可根据“”来判定;
当,则时,可根据“”来判定.
故选:.
8.(2021春 莲湖区期末)如图,是的边的中点,过点作,过点作直线交于,交于,若,,则的长为
A.1 B.2 C.2.5 D.3
【解答】证明:,
,,
点为的中点,
,
在和中
,
,
,
,
,
故选:.
9.(2021春 雁塔区校级期末)如图,点在正方形的对角线上,且,直角三角形的两直角边、,分别交、于点、,若正方形的边长为,则重叠部分四边形的面积为
A. B. C. D.
【解答】解:过作于点,于点,
四边形是正方形,
,
又,
,
,
三角形是直角三角形,
,
,
是的角平分线,,
,四边形是正方形,
在和中,
,
,
四边形的面积等于正方形的面积,
正方形的边长为,
,
,
,
,
正方形的面积,
四边形的面积,
故选:.
10.(2020秋 仓山区期末)如图,中,,过点作射线,在射线上取一点,使得,过点作射线的垂线,垂足为点,连接,若,,则的长度为
A. B. C. D.
【解答】解:如图,连接,过点作交于.
,,
,
在中,
,
,
,,
在和,
,
,
,
,
故选:.
二.填空题(共8小题)
11.(2021 南昌模拟)如图,点在上,,,,则 67.5 .
【解答】解:,
,
在和中,
,
,
,,
,
,
故答案为67.5.
12.(2021春 铜梁区校级期末)如图,在△ABC和△EBD中,AB=EB,AC=ED,若再添加一个条件,则下列条件中能使得△ABC与△EBD全等的有 .
①BC=BD;②∠C=∠D;③∠A=∠E;④∠ABC=∠DBE=90°.
解:∵AB=EB,AC=ED,
∴当BC=BD时,可根据“SSS”可证△ABC≌△EBD;
当∠C=∠D时,无法证明△ABC≌△EBD;
当∠A=∠E时,可根据“SAS”可证△ABC≌△EBD;
当∠ABC=∠DBE=90°,可根据“HL”可证△ABC≌△EBD;
故答案为①③④.
13.(2021春 晋中期末)如图,在中,,为线段上一动点(不与点、重合),连接,作,且,连接,当,时, 24 度.
【解答】解:,
,
即,
在和中,
,
,
,
,
,
,
,
是等边三角形,
,
是等边三角形,
,
,
故答案为:24.
14.(2021 阿城区模拟)如图,中,,和分别为和的角平分线,若的周长为20,,则的长为 8 .
【解答】解:平分,
,
,
,
,
①,
过点作交于点,如图所示:
则,,
,
,
,
平分,
,
在与中,,
,
,,
②,
由①②可得,;
的周长为20,,
,
;
故答案为:8.
15.(2021春 黄陂区期末)如图,点,分别为长方形纸片的边,上的点,将纸片沿翻折,点,分别落在点,处.下列结论一定正确的有 ①③ (填序号即可).
①;
②;
③;
④若的度数比的2倍还多,则的度数为.
【解答】解:由折叠的性质可得:,
又由矩形的性质可得,
,
,故①正确;
设,
则,,
,
,
,故②错误;
,
,故③正确;
的度数比的2倍还多,
,解得:,
,故④错误.
综上所述,①③正确,
故答案为:①③.
16.(2021春 和平区期末)如图,在中,,,,与相交于点,连接并延长交于点,的平分线交的延长线于点,连接,则下列结论:
①;②;③;④;
⑤.其中正确的是 ①②③④⑤ .(只填写序号)
【解答】解:①,,
,
,故①正确;
②是的角平分线,
,
,
,
,
,
是的垂直平分线,
;故②正确;
(3),,
,
,
,,
,
,
在与中,
,
,故③正确;
④,
,
;故④正确;
⑤,
.
,故⑤正确.
综上所述①②③④⑤正确.
故答案为:①②③④⑤.
17.(2021春 龙岗区期末)如图,在中,为的中点,是上一点,连接并延长交于,,且,,则的长度为 .
【解答】解:如图,延长到使,连接,
为的中点,
,
在与中,
,
,
,,
,
,
,
,
.
,
,
即,
,
故答案为.
18.(2021春 历下区期末)如图,AB=4cm,AC=BD=3cm,∠CAB=∠DBA,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,设运动时间为t(s),则当△ACP与△BPQ全等时,点Q的运动速度为
解:设点Q的运动速度为x cm/s,则BQ=tx(cm),
∵AP=t cm,
∴PB=(4-t)cm,
∵∠A=∠B,
∴当AC=BP,AP=BQ,则可根据“SAS”判断△ACP≌△BPQ,
即4-t=3,t=tx,解得t=1,x=1;
当AC=BQ,AP=BP,则可根据“SAS”判断△ACP≌△BQP,
即3=tx,t=4-t,解得t=2,x=1.5;
综上所述,点Q的运动速度为1s/cm或1.5s/cm.
故选:B、C.
三.解答题(共6小题)
19.(2021 泰兴市模拟)如图,点、分别在、上,、相交于点, ①③ .求证:.
在“①;②;③”这三个条件中选择两个填入上面的横线上
(只要填写序号),并完成解答.
【解答】解:想证,考虑证明,已知条件中有公共角,给出的3个选择条件都是边对应相等,因此只能考虑判定,因此选①③.
证明:在△和中,
,
,
.
故答案为:①③.
20.(2021 广东二模)如图,,,,求证:.
【解答】证明:,
,
,
在和中,
,
,
.
21.(2021 南岗区模拟)已知:点,在上,,,.
(1)如图1,求证:;
(2)如图2,连接,,,,在不添加任何辅助线的情况下,请直接写出图2中的四组平行线.
【解答】(1)证明:,
,
即,
,
,
在和中,
,
,
;
(2)解:图2中的四组平行线为:,,,,理由如下:
由(1)得:,
,,
,
四边形是平行四边形,
,
,
,
,
四边形是平行四边形,
.
22.(2021 南岗区模拟)已知:在和中,,,其中.
(1)如图1,求证:;
(2)如图2,,分别交,于点,,交于点,在不添加任何辅助线的情况下,请直接写出图2中的四对全等三角形.
【解答】证明:(1),
,
即,
在与中,
,
,
;
(2)由(1)得,
,,,,
,
,
,
,
在与中,
,
,
,
在与中,
,
,
,
,,
,
在与中,
,
.
23.(2021 镇海区模拟)如图,已知和均是直角三角形,,,于点.
(1)求证:;
【解答】(1)证明:,
,
,
,
,
,
在和中,
,
;
24.(2020秋 宜宾期末)在中,,,,点在上,且,过点作射线与在同侧),若动点从点出发,沿射线匀速运动,运动速度为,设点运动时间为秒.连接、.
(1)如图①,当时,求证:;
(2)如图②,当于点时,求此时的值.
【解答】(1)证明:如图①,,
,
,
又,
,
,
又,
,
,
又,,
,
在和中,
,
;
(2)解:如图②,,
,
,
又,
,
,
在和中,
,
,
,
,
,.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
三角形的初步认识——1.5全等三角形的判定
一.选择题(共10小题)
1.(2021春 祥符区期末)如图,已知,下列所给条件不一定能使与全等的是
A. B. C. D.
2.(2021春 锦江区校级期末)如图,已知三条边、三个角,则甲、乙两个三角形中,与全等的图形是
A.甲 B.乙 C.甲和乙 D.都不是
3.(2021春 历城区期末)如图,用纸板挡住了三角形的一部分,小明根据所学知识很快就重新画出了一个与原来完全一样的三角形,他的依据是
A. B. C. D.
4.(2021春 九龙坡区校级期末)如图,、、、四点在同一直线上,在和中,,,添加下列条件,仍不能证明的是
A. B. C. D.
5.(2021春 砀山县期末)一块三角形玻璃样板不慎被张字同学碰破,成了四片完整碎片(如图所示),聪明的他经过仔细地考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板,你认为下列四个答案中考虑最全面的是
A.带1,2或2,3去就可以了 B.带1,4或3,4去就可以了
C.带1,4或2,4或3,4去均可 D.带其中的任意两块去都可以
6.(2020秋 射阳县期末)工人师傅常用角尺平分一个任意角.作法如下:如图所示,是一个任意角,在边,上分别取,移动角尺,使角尺两边相同的刻度分别与,重合,过角尺顶点的射线即是的平分线.这种作法的道理是
A. B. C. D.
7.(2021春 乐平市期末)如图,已知,,点、、、四点在同一直线上.要利用“”来判定,下列四个条件:①;②;③;④.可以利用的是
A.①② B.②④ C.②③ D.①④
8.(2021春 莲湖区期末)如图,是的边的中点,过点作,过点作直线交于,交于,若,,则的长为
A.1 B.2 C.2.5 D.3
9.(2021春 雁塔区校级期末)如图,点在正方形的对角线上,且,直角三角形的两直角边、,分别交、于点、,若正方形的边长为,则重叠部分四边形的面积为
A. B. C. D.
10.(2020秋 仓山区期末)如图,中,,过点作射线,在射线上取一点,使得,过点作射线的垂线,垂足为点,连接,若,,则的长度为
A. B. C. D.
二.填空题(共8小题)
11.(2021 南昌模拟)如图所示,已知点在上,,,,则
.
12.(2021春 铜梁区校级期末)如图,在△ABC和△EBD中,AB=EB,AC=ED,若再添加一个条件,则下列条件中能使得△ABC与△EBD全等的有 .
①BC=BD;②∠C=∠D;③∠A=∠E;④∠ABC=∠DBE=90°.
13.(2021春 晋中期末)如图,在中,,为线段上一动点(不与点、重合),连接,作,且,连接,当,时, 度.
14.(2021 阿城区模拟)如图,中,,和分别为和的角平分线,若的周长为20,,则的长为 .
15.(2021春 黄陂区期末)如图,点,分别为长方形纸片的边,上的点,将纸片沿翻折,点,分别落在点,处.下列结论一定正确的有 (填序号即可).
①;
②;
③;
④若的度数比的2倍还多,则的度数为.
16.(2021春 和平区期末)如图,在中,,,,与相交于点,连接并延长交于点,的平分线交的延长线于点,连接,则下列结论:
①;②;③;④;
⑤.其中正确的是 .(只填写序号)
17.(2021春 龙岗区期末)如图,在中,为的中点,是上一点,连接并延长交于,,且,,则的长度为 .
18.(2021春 历下区期末)如图,AB=4cm,AC=BD=3cm,∠CAB=∠DBA,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,设运动时间为t(s),则当△ACP与△BPQ全等时,点Q的运动速度为
三.解答题(共6小题)
19.(2021 泰兴市模拟)如图,点、分别在、上,、相交于点, .求证:.
在“①;②;③”这三个条件中选择两个填入上面的横线上
(只要填写序号),并完成解答.
20.(2021 广东二模)如图,,,,求证:.
21.(2021 南岗区模拟)已知:点,在上,,,.
(1)如图1,求证:;
(2)如图2,连接,,,,在不添加任何辅助线的情况下,请直接写出图2中的四组平行线.
22.(2021 南岗区模拟)已知:在和中,,,其中.
(1)如图1,求证:;
(2)如图2,,分别交,于点,,交于点,在不添加任何辅助线的情况下,请直接写出图2中的四对全等三角形.
23.(2021 镇海区模拟)如图,已知和均是直角三角形,,,于点.求证:;
24.(2020秋 宜宾期末)在中,,,,点在上,且,过点作射线与在同侧),若动点从点出发,沿射线匀速运动,运动速度为,设点运动时间为秒.连接、.
(1)如图①,当时,求证:;
(2)如图②,当于点时,求此时的值.
三角形的初步认识——1.5全等三角形的判定
参考答案与试题解析
一.选择题(共10小题)
1.(2021春 祥符区期末)如图,已知,下列所给条件不一定能使与全等的是
A. B. C. D.
【解答】解:由图可得,
,
又,
当时,,故选项不符合题意;
当时,和不一定全等,故选项符合题意;
当时,,故选项不符合题意;
当时,,故选项不符合题意;
故选:.
2.(2021春 锦江区校级期末)如图,已知三条边、三个角,则甲、乙两个三角形中,与全等的图形是
A.甲 B.乙 C.甲和乙 D.都不是
【解答】解:甲三角形夹边的两角分别与已知三角形对应相等,故甲与全等;
乙三角形内角及所对边与对应相等且均有内角,可根据判定乙与全等;
则与全等的有乙和甲,
故选:.
3.(2021春 历城区期末)如图,用纸板挡住了三角形的一部分,小明根据所学知识很快就重新画出了一个与原来完全一样的三角形,他的依据是
A. B. C. D.
【解答】解:如图,
只要量出的长和和的度数,再画出一个三角形,使,,即可,
故选:.
4.(2021春 九龙坡区校级期末)如图,、、、四点在同一直线上,在和中,,,添加下列条件,仍不能证明的是
A. B. C. D.
【解答】解:,,
若添加,则两个三角形满足,
不一定全对,符合题意;
若添加:,则两个三角形全等,不符合题意;
若添加,则,则两个三角形全等,不符合题意;
若添加,则,则两个三角形全等,不符合题意;
故选:.
5.(2021春 砀山县期末)一块三角形玻璃样板不慎被张字同学碰破,成了四片完整碎片(如图所示),聪明的他经过仔细地考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板,你认为下列四个答案中考虑最全面的是
A.带1,2或2,3去就可以了 B.带1,4或3,4去就可以了
C.带1,4或2,4或3,4去均可 D.带其中的任意两块去都可以
【解答】解:带3、4可以用“角边角”确定三角形,
带1、4可以用“角边角”确定三角形,
带2、4可以延长还原出原三角形,
故选:.
6.(2020秋 射阳县期末)工人师傅常用角尺平分一个任意角.作法如下:如图所示,是一个任意角,在边,上分别取,移动角尺,使角尺两边相同的刻度分别与,重合,过角尺顶点的射线即是的平分线.这种作法的道理是
A. B. C. D.
【解答】解:由图可知,,又,为公共边,
,
,
即即是的平分线.
故选:.
7.(2021春 乐平市期末)如图,已知,,点、、、四点在同一直线上.要利用“”来判定,下列四个条件:①;②;③;④.可以利用的是
A.①② B.②④ C.②③ D.①④
【解答】解:,
,即,
,
当时,可根据“”来判定;
当,则时,可根据“”来判定.
故选:.
8.(2021春 莲湖区期末)如图,是的边的中点,过点作,过点作直线交于,交于,若,,则的长为
A.1 B.2 C.2.5 D.3
【解答】证明:,
,,
点为的中点,
,
在和中
,
,
,
,
,
故选:.
9.(2021春 雁塔区校级期末)如图,点在正方形的对角线上,且,直角三角形的两直角边、,分别交、于点、,若正方形的边长为,则重叠部分四边形的面积为
A. B. C. D.
【解答】解:过作于点,于点,
四边形是正方形,
,
又,
,
,
三角形是直角三角形,
,
,
是的角平分线,,
,四边形是正方形,
在和中,
,
,
四边形的面积等于正方形的面积,
正方形的边长为,
,
,
,
,
正方形的面积,
四边形的面积,
故选:.
10.(2020秋 仓山区期末)如图,中,,过点作射线,在射线上取一点,使得,过点作射线的垂线,垂足为点,连接,若,,则的长度为
A. B. C. D.
【解答】解:如图,连接,过点作交于.
,,
,
在中,
,
,
,,
在和,
,
,
,
,
故选:.
二.填空题(共8小题)
11.(2021 南昌模拟)如图,点在上,,,,则 67.5 .
【解答】解:,
,
在和中,
,
,
,,
,
,
故答案为67.5.
12.(2021春 铜梁区校级期末)如图,在△ABC和△EBD中,AB=EB,AC=ED,若再添加一个条件,则下列条件中能使得△ABC与△EBD全等的有 .
①BC=BD;②∠C=∠D;③∠A=∠E;④∠ABC=∠DBE=90°.
解:∵AB=EB,AC=ED,
∴当BC=BD时,可根据“SSS”可证△ABC≌△EBD;
当∠C=∠D时,无法证明△ABC≌△EBD;
当∠A=∠E时,可根据“SAS”可证△ABC≌△EBD;
当∠ABC=∠DBE=90°,可根据“HL”可证△ABC≌△EBD;
故答案为①③④.
13.(2021春 晋中期末)如图,在中,,为线段上一动点(不与点、重合),连接,作,且,连接,当,时, 24 度.
【解答】解:,
,
即,
在和中,
,
,
,
,
,
,
,
是等边三角形,
,
是等边三角形,
,
,
故答案为:24.
14.(2021 阿城区模拟)如图,中,,和分别为和的角平分线,若的周长为20,,则的长为 8 .
【解答】解:平分,
,
,
,
,
①,
过点作交于点,如图所示:
则,,
,
,
,
平分,
,
在与中,,
,
,,
②,
由①②可得,;
的周长为20,,
,
;
故答案为:8.
15.(2021春 黄陂区期末)如图,点,分别为长方形纸片的边,上的点,将纸片沿翻折,点,分别落在点,处.下列结论一定正确的有 ①③ (填序号即可).
①;
②;
③;
④若的度数比的2倍还多,则的度数为.
【解答】解:由折叠的性质可得:,
又由矩形的性质可得,
,
,故①正确;
设,
则,,
,
,
,故②错误;
,
,故③正确;
的度数比的2倍还多,
,解得:,
,故④错误.
综上所述,①③正确,
故答案为:①③.
16.(2021春 和平区期末)如图,在中,,,,与相交于点,连接并延长交于点,的平分线交的延长线于点,连接,则下列结论:
①;②;③;④;
⑤.其中正确的是 ①②③④⑤ .(只填写序号)
【解答】解:①,,
,
,故①正确;
②是的角平分线,
,
,
,
,
,
是的垂直平分线,
;故②正确;
(3),,
,
,
,,
,
,
在与中,
,
,故③正确;
④,
,
;故④正确;
⑤,
.
,故⑤正确.
综上所述①②③④⑤正确.
故答案为:①②③④⑤.
17.(2021春 龙岗区期末)如图,在中,为的中点,是上一点,连接并延长交于,,且,,则的长度为 .
【解答】解:如图,延长到使,连接,
为的中点,
,
在与中,
,
,
,,
,
,
,
,
.
,
,
即,
,
故答案为.
18.(2021春 历下区期末)如图,AB=4cm,AC=BD=3cm,∠CAB=∠DBA,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,设运动时间为t(s),则当△ACP与△BPQ全等时,点Q的运动速度为
解:设点Q的运动速度为x cm/s,则BQ=tx(cm),
∵AP=t cm,
∴PB=(4-t)cm,
∵∠A=∠B,
∴当AC=BP,AP=BQ,则可根据“SAS”判断△ACP≌△BPQ,
即4-t=3,t=tx,解得t=1,x=1;
当AC=BQ,AP=BP,则可根据“SAS”判断△ACP≌△BQP,
即3=tx,t=4-t,解得t=2,x=1.5;
综上所述,点Q的运动速度为1s/cm或1.5s/cm.
故选:B、C.
三.解答题(共6小题)
19.(2021 泰兴市模拟)如图,点、分别在、上,、相交于点, ①③ .求证:.
在“①;②;③”这三个条件中选择两个填入上面的横线上
(只要填写序号),并完成解答.
【解答】解:想证,考虑证明,已知条件中有公共角,给出的3个选择条件都是边对应相等,因此只能考虑判定,因此选①③.
证明:在△和中,
,
,
.
故答案为:①③.
20.(2021 广东二模)如图,,,,求证:.
【解答】证明:,
,
,
在和中,
,
,
.
21.(2021 南岗区模拟)已知:点,在上,,,.
(1)如图1,求证:;
(2)如图2,连接,,,,在不添加任何辅助线的情况下,请直接写出图2中的四组平行线.
【解答】(1)证明:,
,
即,
,
,
在和中,
,
,
;
(2)解:图2中的四组平行线为:,,,,理由如下:
由(1)得:,
,,
,
四边形是平行四边形,
,
,
,
,
四边形是平行四边形,
.
22.(2021 南岗区模拟)已知:在和中,,,其中.
(1)如图1,求证:;
(2)如图2,,分别交,于点,,交于点,在不添加任何辅助线的情况下,请直接写出图2中的四对全等三角形.
【解答】证明:(1),
,
即,
在与中,
,
,
;
(2)由(1)得,
,,,,
,
,
,
,
在与中,
,
,
,
在与中,
,
,
,
,,
,
在与中,
,
.
23.(2021 镇海区模拟)如图,已知和均是直角三角形,,,于点.
(1)求证:;
【解答】(1)证明:,
,
,
,
,
,
在和中,
,
;
24.(2020秋 宜宾期末)在中,,,,点在上,且,过点作射线与在同侧),若动点从点出发,沿射线匀速运动,运动速度为,设点运动时间为秒.连接、.
(1)如图①,当时,求证:;
(2)如图②,当于点时,求此时的值.
【解答】(1)证明:如图①,,
,
,
又,
,
,
又,
,
,
又,,
,
在和中,
,
;
(2)解:如图②,,
,
,
又,
,
,
在和中,
,
,
,
,
,.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
