浙教版九年级数学上册 4.6 相似多边形 同步测试题(含答案)
文档属性
| 名称 | 浙教版九年级数学上册 4.6 相似多边形 同步测试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 86.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 00:00:00 | ||
图片预览



文档简介
4.6
相似多边形
同步测试题
(满分120分;时间:120分钟)
真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!
题号
一
二
三
总分
得分
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
两个多边形相似的条件是(
)
A.对应角相等
B.对应边成比例
C.对应角相等或对应边成比例
D.对应角相等且对应边成比例
?
2.
制作一块长方形广告牌的成本是元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的倍,那么扩大后长方形广告牌的成本是(?
?
?
?
)
A.元
B.元
C.元
D.元
?
3.
矩形甲、乙、丙的长和宽如图所示(单位:),则其中是相似图形的是(
)
A.甲和乙
B.乙和丙
C.丙和甲
D.甲、乙和丙
?
4.
两个相似多边形的面积比是,其中小多边形的周长为,则较大多边形的周长为(
)
A.
B.
C.
D.
?
5.
在一场赈灾演出中,根据需要必须用灯光照亮舞台中一个半径为米的圆形区域,但由于当地条件简陋,当时没有这样的灯,舞台监督要求用另一种可照半径为米的灯代替,那么至少需这样的代用灯(
)
A.盏
B.盏
C.盏
D.盏
?6.
将一个五角星图片放大,当面积扩大为原来的倍时,周长扩大为原来的(
)
A.倍
B.倍
C.倍
D.倍
?
7.
如图,矩形的面积是,点在上,点在上,且,,则矩形的面积是(
)
A.
B.
C.
D.
?
8.
下列说法中不一定正确的是(
)
A.相似的图形大小可以相等
B.所有等边三角形均相似
C.所有正方形均相似
D.所有菱形均相似
?
9.
两相似四边形的面积比为,周长和是,则这两个四边形周长分别是(
)
A.和
B.和
C.和
D.和
?
10.
如图所示,将矩形沿两条较长边的中点的连线对折,如果矩形与矩形相似,那么等于(
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
两个相似的五边形,一个各边长分别为,,,,,另一个五边形的最长边为,则后一个五边形的周长为________.
?
12.
沿一张矩形纸较长两边的中点对折后,再对折一次,使两次的折痕平行.如果这两次对折后得到的矩形与原来的矩形纸相似,那么原来矩形纸的长与宽的比为________.
?
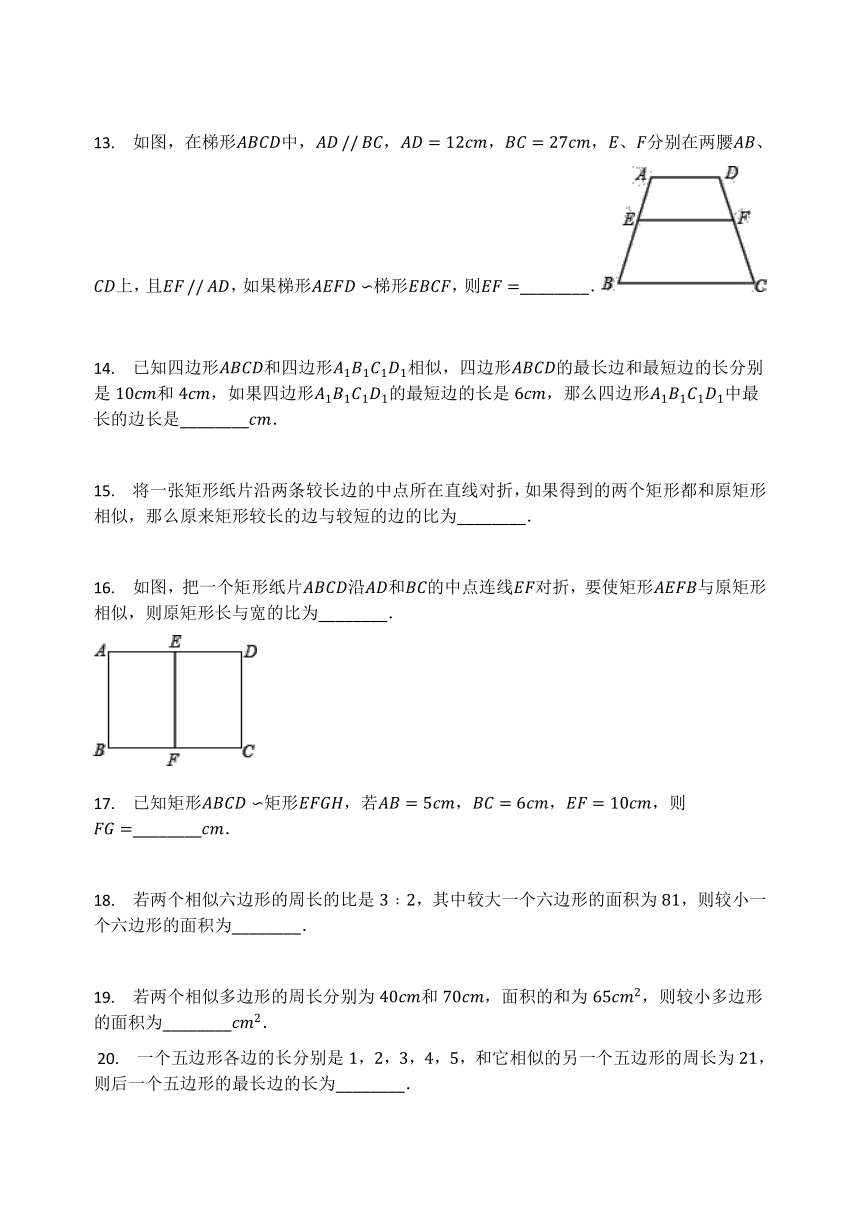
13.
如图,在梯形中,,,,、分别在两腰、上,且,如果梯形梯形,则________.
?
14.
已知四边形和四边形相似,四边形的最长边和最短边的长分别是和,如果四边形的最短边的长是,那么四边形中最长的边长是________.
?
15.
将一张矩形纸片沿两条较长边的中点所在直线对折,如果得到的两个矩形都和原矩形相似,那么原来矩形较长的边与较短的边的比为________.
?
16.
如图,把一个矩形纸片沿和的中点连线对折,要使矩形与原矩形相似,则原矩形长与宽的比为________.
?
17.
已知矩形矩形,若,,,则________.
?
18.
若两个相似六边形的周长的比是﹕,其中较大一个六边形的面积为,则较小一个六边形的面积为________.
?
19.
若两个相似多边形的周长分别为和,面积的和为,则较小多边形的面积为________.
?20.
一个五边形各边的长分别是,,,,,和它相似的另一个五边形的周长为,则后一个五边形的最长边的长为________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
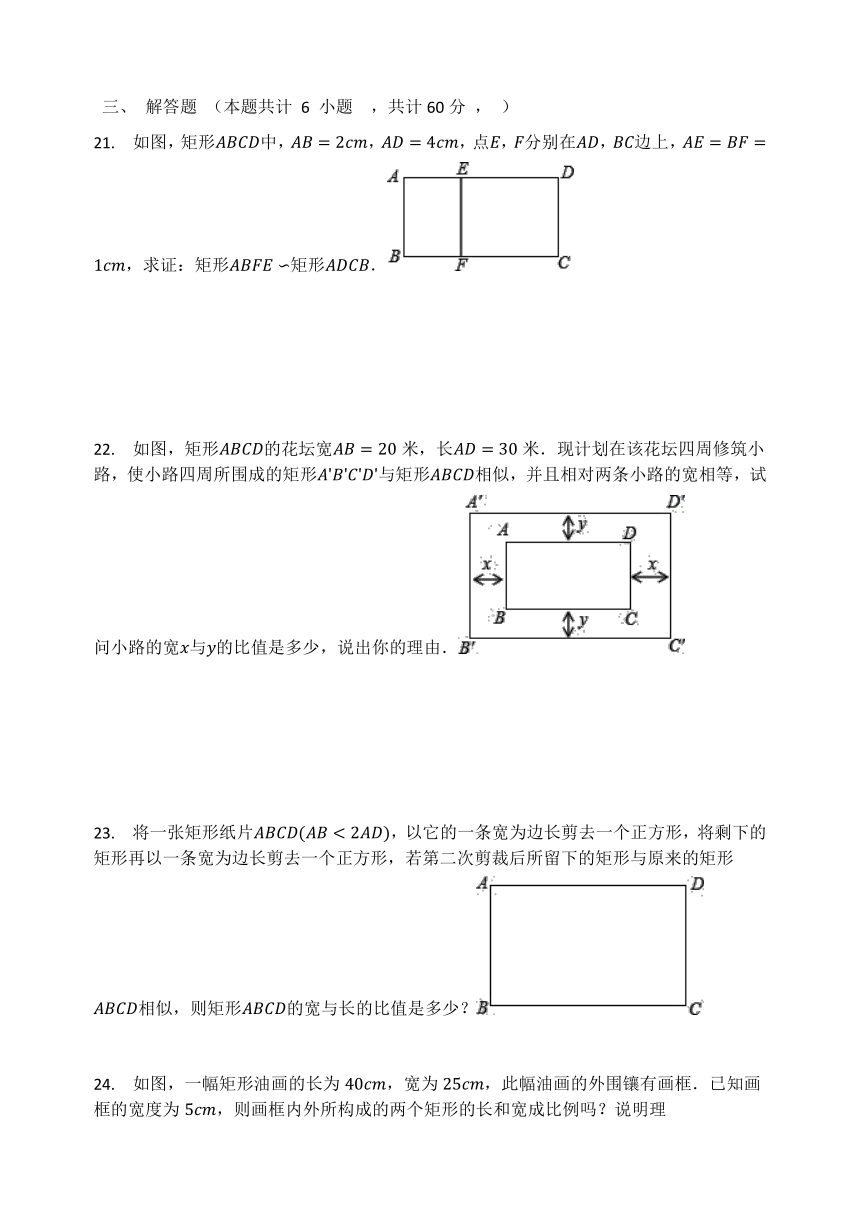
21.
如图,矩形中,,,点,分别在,边上,,求证:矩形矩形.
?
22.
如图,矩形的花坛宽米,长米.现计划在该花坛四周修筑小路,使小路四周所围成的矩形与矩形相似,并且相对两条小路的宽相等,试问小路的宽与的比值是多少,说出你的理由.
?
23.
将一张矩形纸片,以它的一条宽为边长剪去一个正方形,将剩下的矩形再以一条宽为边长剪去一个正方形,若第二次剪裁后所留下的矩形与原来的矩形相似,则矩形的宽与长的比值是多少?
?
24.
如图,一幅矩形油画的长为,宽为,此幅油画的外围镶有画框.已知画框的宽度为,则画框内外所构成的两个矩形的长和宽成比例吗?说明理由.
?
25.
如图,已知在梯形中,,,,若把梯形分成的两个小梯形相似,求的长.
?
26.
善于学习的小敏查资料知道:对应角相等,对应边成比例的两个梯形,叫做相似梯形.他想到“平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似”,提出如下两个问题,你能帮助解决吗?
问题一:平行于梯形底边的直线截两腰所得的小梯形和原梯形是否相似?
(1)从特殊情形入手探究.假设梯形中,,,,,,是中位线(如图①).根据相似梯形的定义,请你说明梯形与梯形是否相似;
(2)一般结论:平行于梯形底边的直线截两腰所得的梯形与原梯形________;(填“相似”或“不相似”或“相似性无法确定”.不要求证明)
问题二:平行于梯形底边的直线截两腰所得的两个小梯形是否相似?
(1)从特殊平行线入手探究.梯形的中位线截两腰所得的两个小梯形________;(填“相似”或“不相似”或“相似性无法确定”.不要求证明)
(2)从特殊梯形入手探究.同上假设,梯形中,,,,,,你能找到与梯形底边平行的直线(点,在梯形的两腰上,如图②),使得梯形与梯形相似吗?请根据相似梯形的定义说明理由;
(3)一般结论:对于任意梯形(如图③),一定________(填“存在”或“不存在”)平行于梯形底边的直线,使截得的两个小梯形相似.若存在,则确定这条平行线位置的条件是________.(不妨设,,,.不要求证明)
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【解答】
解:∵
对应角相等且对应边成比例的多边形相似,
∴
符合定义,
故选.
2.
【解答】
解:,
∴
长方形广告牌的成本是元,
将此广告牌的四边都扩大为原来的倍,
则面积扩大为原来的倍,
∴
扩大后长方形广告牌的面积,
∴
扩大后长方形广告牌的成本是元.
故选.
3.
【解答】
解:矩形甲的长宽比为:;
矩形甲的长宽比为:;
矩形甲的长宽比为:;
故矩形甲和丙为相似图形.
故选.
4.
【解答】
两个相似多边形的面积比是,
面积比是周长比的平方,
则大多边形与小多边形的相似比是.
相似多边形周长的比等于相似比,
因而设大多边形的周长为,
则有,
解得:=.
大多边形的周长为.
5.
【解答】
解:如图,设半径为的圆的圆心是,在圆周上作正六边形,其边长都是.再分别以各边中点为圆心作六个半径为的圆.
所以共需盏灯.
故选.
6.
【解答】
解:∵
面积扩大为原来的倍,
∴
相似比为,
∴
周长扩大为原来的倍.
故选.
7.
【解答】
解:∵
,,
∴
,,
又∵
矩形的四个角都是直角,
∴
矩形矩形,
∴
,
即,
解得.
故选.
8.
【解答】
解:、如全等三角形,正确;
、对应的角和边的比均对应相等,正确;
、符合多边形相似的定义,对应边的比和角都相等,正确;
、所有的菱形的边的比相等而对应角的比不一定相等,因而菱形不一定相似.
故选.
9.
【解答】
解:∵
两相似四边形的面积比为,面积之比等于相似比的平方.
∴
四边形周长比为,
这两个四边形周长分别是,.故选.
10.
【解答】
解:根据矩形相似,对应边的比相等得到:,
即:,
则,
∴
,
∴
,
则.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【解答】
解:设所求五边形的周长为,
∵
一个五边形的各边长分别为,,,,,另一个五边形的最长边为,
∴
两个五边形的相似比.
∵
第一个五边形的周长,
∴
,解得.
故答案为.
12.
【解答】
解:
设原来矩形的长为,宽为,
则可知两次对折后得到的矩形的长为,宽为,
∵
这两次对折后得到的矩形与原来的矩形纸相似,
∴
,可得,
∴
,
∴
,
即原来矩形的长与宽的比为,
故答案为:.
13.
【解答】
解:∵
梯形梯形,
∴
,
∵
,,
∴
,
∴
,
∴
.
故答案为.
14.
【解答】
解:∵
四边形和四边形相似,四边形的最长边和最短边的长分别是和,
四边形的最短边的长是,
∴
两多边形的相似比为:,
那么四边形中最长的边长是:.
故答案为:.
15.
【解答】
解:设原来矩形的长为,宽为,
则对折后的矩形的长为,宽为,
∵
得到的两个矩形都和原矩形相似,
∴
,
解得.
16.
【解答】
根据条件可知:矩形矩形.
∴
.
设=,=,则.则,即:=.
∴
.
∴
.
即原矩形长与宽的比为.
17.
【解答】
解:∵
矩形矩形.
∴
,即
解得:.
18.
【解答】
解:∵
两个相似六边形的周长的比是﹕,
∴
它们的面积的比为,
∵
较大一个六边形的面积为,
∴
较小一个六边形的面积为;
故答案为:.
19.
【解答】
解:设较小多边形的面积为,则较大多边形的面积为,
∵
两个相似多边形的周长分别为和,
∴
其相似比,
∴
,
解得.
故答案为:.
20.
【解答】
解:,
设后一个五边形的最长边的长为,
则,
解得.
故答案为:.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【解答】
证明:∵
四边形是矩形,
∴
,,,,
即,
∵
,
∴
四边形是矩形,
∴
,,
∴
,,,,,
∴
矩形矩形.
22.
【解答】
解:∵
相对两条小路的宽均相等,
∴
,;
∵
矩形矩形,
∴
,
又∵
米,米,小路的宽为与,
∴
:,
解得.
23.
【解答】
解:根据题意画图如下:
设,,则,,若矩形矩形,
则:,
解得:,
若矩形矩形,则
,
解得:.
24.
【解答】
解:∵
油画的长为,宽为,画框的宽度为,
∴
整幅画的长为,宽为,
∴
长的比为,
宽的比为,
∴
不成比例.
25.
【解答】
解:∵
把梯形分成的两个小梯形相似,
∴
,
∴
,
∴
.
26.
【解答】
解:问题一:(1)两个梯形的腰相等,
即腰的比是,而上底的比是,
因而这两个梯形一定不相似;
(2)不相似.
问题二:(1)不相似;
(2)梯形与梯形相似,
∴
,即
解得:.
∵
.
又∵
,
∴
(3)如果梯形梯形,
则,,
∵
,,
∴
,
∴
.
相似多边形
同步测试题
(满分120分;时间:120分钟)
真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!
题号
一
二
三
总分
得分
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
两个多边形相似的条件是(
)
A.对应角相等
B.对应边成比例
C.对应角相等或对应边成比例
D.对应角相等且对应边成比例
?
2.
制作一块长方形广告牌的成本是元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的倍,那么扩大后长方形广告牌的成本是(?
?
?
?
)
A.元
B.元
C.元
D.元
?
3.
矩形甲、乙、丙的长和宽如图所示(单位:),则其中是相似图形的是(
)
A.甲和乙
B.乙和丙
C.丙和甲
D.甲、乙和丙
?
4.
两个相似多边形的面积比是,其中小多边形的周长为,则较大多边形的周长为(
)
A.
B.
C.
D.
?
5.
在一场赈灾演出中,根据需要必须用灯光照亮舞台中一个半径为米的圆形区域,但由于当地条件简陋,当时没有这样的灯,舞台监督要求用另一种可照半径为米的灯代替,那么至少需这样的代用灯(
)
A.盏
B.盏
C.盏
D.盏
?6.
将一个五角星图片放大,当面积扩大为原来的倍时,周长扩大为原来的(
)
A.倍
B.倍
C.倍
D.倍
?
7.
如图,矩形的面积是,点在上,点在上,且,,则矩形的面积是(
)
A.
B.
C.
D.
?
8.
下列说法中不一定正确的是(
)
A.相似的图形大小可以相等
B.所有等边三角形均相似
C.所有正方形均相似
D.所有菱形均相似
?
9.
两相似四边形的面积比为,周长和是,则这两个四边形周长分别是(
)
A.和
B.和
C.和
D.和
?
10.
如图所示,将矩形沿两条较长边的中点的连线对折,如果矩形与矩形相似,那么等于(
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
两个相似的五边形,一个各边长分别为,,,,,另一个五边形的最长边为,则后一个五边形的周长为________.
?
12.
沿一张矩形纸较长两边的中点对折后,再对折一次,使两次的折痕平行.如果这两次对折后得到的矩形与原来的矩形纸相似,那么原来矩形纸的长与宽的比为________.
?
13.
如图,在梯形中,,,,、分别在两腰、上,且,如果梯形梯形,则________.
?
14.
已知四边形和四边形相似,四边形的最长边和最短边的长分别是和,如果四边形的最短边的长是,那么四边形中最长的边长是________.
?
15.
将一张矩形纸片沿两条较长边的中点所在直线对折,如果得到的两个矩形都和原矩形相似,那么原来矩形较长的边与较短的边的比为________.
?
16.
如图,把一个矩形纸片沿和的中点连线对折,要使矩形与原矩形相似,则原矩形长与宽的比为________.
?
17.
已知矩形矩形,若,,,则________.
?
18.
若两个相似六边形的周长的比是﹕,其中较大一个六边形的面积为,则较小一个六边形的面积为________.
?
19.
若两个相似多边形的周长分别为和,面积的和为,则较小多边形的面积为________.
?20.
一个五边形各边的长分别是,,,,,和它相似的另一个五边形的周长为,则后一个五边形的最长边的长为________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
如图,矩形中,,,点,分别在,边上,,求证:矩形矩形.
?
22.
如图,矩形的花坛宽米,长米.现计划在该花坛四周修筑小路,使小路四周所围成的矩形与矩形相似,并且相对两条小路的宽相等,试问小路的宽与的比值是多少,说出你的理由.
?
23.
将一张矩形纸片,以它的一条宽为边长剪去一个正方形,将剩下的矩形再以一条宽为边长剪去一个正方形,若第二次剪裁后所留下的矩形与原来的矩形相似,则矩形的宽与长的比值是多少?
?
24.
如图,一幅矩形油画的长为,宽为,此幅油画的外围镶有画框.已知画框的宽度为,则画框内外所构成的两个矩形的长和宽成比例吗?说明理由.
?
25.
如图,已知在梯形中,,,,若把梯形分成的两个小梯形相似,求的长.
?
26.
善于学习的小敏查资料知道:对应角相等,对应边成比例的两个梯形,叫做相似梯形.他想到“平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似”,提出如下两个问题,你能帮助解决吗?
问题一:平行于梯形底边的直线截两腰所得的小梯形和原梯形是否相似?
(1)从特殊情形入手探究.假设梯形中,,,,,,是中位线(如图①).根据相似梯形的定义,请你说明梯形与梯形是否相似;
(2)一般结论:平行于梯形底边的直线截两腰所得的梯形与原梯形________;(填“相似”或“不相似”或“相似性无法确定”.不要求证明)
问题二:平行于梯形底边的直线截两腰所得的两个小梯形是否相似?
(1)从特殊平行线入手探究.梯形的中位线截两腰所得的两个小梯形________;(填“相似”或“不相似”或“相似性无法确定”.不要求证明)
(2)从特殊梯形入手探究.同上假设,梯形中,,,,,,你能找到与梯形底边平行的直线(点,在梯形的两腰上,如图②),使得梯形与梯形相似吗?请根据相似梯形的定义说明理由;
(3)一般结论:对于任意梯形(如图③),一定________(填“存在”或“不存在”)平行于梯形底边的直线,使截得的两个小梯形相似.若存在,则确定这条平行线位置的条件是________.(不妨设,,,.不要求证明)
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【解答】
解:∵
对应角相等且对应边成比例的多边形相似,
∴
符合定义,
故选.
2.
【解答】
解:,
∴
长方形广告牌的成本是元,
将此广告牌的四边都扩大为原来的倍,
则面积扩大为原来的倍,
∴
扩大后长方形广告牌的面积,
∴
扩大后长方形广告牌的成本是元.
故选.
3.
【解答】
解:矩形甲的长宽比为:;
矩形甲的长宽比为:;
矩形甲的长宽比为:;
故矩形甲和丙为相似图形.
故选.
4.
【解答】
两个相似多边形的面积比是,
面积比是周长比的平方,
则大多边形与小多边形的相似比是.
相似多边形周长的比等于相似比,
因而设大多边形的周长为,
则有,
解得:=.
大多边形的周长为.
5.
【解答】
解:如图,设半径为的圆的圆心是,在圆周上作正六边形,其边长都是.再分别以各边中点为圆心作六个半径为的圆.
所以共需盏灯.
故选.
6.
【解答】
解:∵
面积扩大为原来的倍,
∴
相似比为,
∴
周长扩大为原来的倍.
故选.
7.
【解答】
解:∵
,,
∴
,,
又∵
矩形的四个角都是直角,
∴
矩形矩形,
∴
,
即,
解得.
故选.
8.
【解答】
解:、如全等三角形,正确;
、对应的角和边的比均对应相等,正确;
、符合多边形相似的定义,对应边的比和角都相等,正确;
、所有的菱形的边的比相等而对应角的比不一定相等,因而菱形不一定相似.
故选.
9.
【解答】
解:∵
两相似四边形的面积比为,面积之比等于相似比的平方.
∴
四边形周长比为,
这两个四边形周长分别是,.故选.
10.
【解答】
解:根据矩形相似,对应边的比相等得到:,
即:,
则,
∴
,
∴
,
则.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【解答】
解:设所求五边形的周长为,
∵
一个五边形的各边长分别为,,,,,另一个五边形的最长边为,
∴
两个五边形的相似比.
∵
第一个五边形的周长,
∴
,解得.
故答案为.
12.
【解答】
解:
设原来矩形的长为,宽为,
则可知两次对折后得到的矩形的长为,宽为,
∵
这两次对折后得到的矩形与原来的矩形纸相似,
∴
,可得,
∴
,
∴
,
即原来矩形的长与宽的比为,
故答案为:.
13.
【解答】
解:∵
梯形梯形,
∴
,
∵
,,
∴
,
∴
,
∴
.
故答案为.
14.
【解答】
解:∵
四边形和四边形相似,四边形的最长边和最短边的长分别是和,
四边形的最短边的长是,
∴
两多边形的相似比为:,
那么四边形中最长的边长是:.
故答案为:.
15.
【解答】
解:设原来矩形的长为,宽为,
则对折后的矩形的长为,宽为,
∵
得到的两个矩形都和原矩形相似,
∴
,
解得.
16.
【解答】
根据条件可知:矩形矩形.
∴
.
设=,=,则.则,即:=.
∴
.
∴
.
即原矩形长与宽的比为.
17.
【解答】
解:∵
矩形矩形.
∴
,即
解得:.
18.
【解答】
解:∵
两个相似六边形的周长的比是﹕,
∴
它们的面积的比为,
∵
较大一个六边形的面积为,
∴
较小一个六边形的面积为;
故答案为:.
19.
【解答】
解:设较小多边形的面积为,则较大多边形的面积为,
∵
两个相似多边形的周长分别为和,
∴
其相似比,
∴
,
解得.
故答案为:.
20.
【解答】
解:,
设后一个五边形的最长边的长为,
则,
解得.
故答案为:.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【解答】
证明:∵
四边形是矩形,
∴
,,,,
即,
∵
,
∴
四边形是矩形,
∴
,,
∴
,,,,,
∴
矩形矩形.
22.
【解答】
解:∵
相对两条小路的宽均相等,
∴
,;
∵
矩形矩形,
∴
,
又∵
米,米,小路的宽为与,
∴
:,
解得.
23.
【解答】
解:根据题意画图如下:
设,,则,,若矩形矩形,
则:,
解得:,
若矩形矩形,则
,
解得:.
24.
【解答】
解:∵
油画的长为,宽为,画框的宽度为,
∴
整幅画的长为,宽为,
∴
长的比为,
宽的比为,
∴
不成比例.
25.
【解答】
解:∵
把梯形分成的两个小梯形相似,
∴
,
∴
,
∴
.
26.
【解答】
解:问题一:(1)两个梯形的腰相等,
即腰的比是,而上底的比是,
因而这两个梯形一定不相似;
(2)不相似.
问题二:(1)不相似;
(2)梯形与梯形相似,
∴
,即
解得:.
∵
.
又∵
,
∴
(3)如果梯形梯形,
则,,
∵
,,
∴
,
∴
.
同课章节目录
