浙教版数学九年级上册 4.2由平行线截得的比例线段 同步课件(28张ppt)
文档属性
| 名称 | 浙教版数学九年级上册 4.2由平行线截得的比例线段 同步课件(28张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
第4章
相似三角形
4.2
由平行线截得的比例线段
你能用直尺和圆规把一条线段三等分吗?
情景导入
学习目标
1.经历基本事实:两条直线被一组平行线
(不少3条)所截,所得的对应线段成比
例的发现过程.
2.掌握上述基本事实,会运用上述基本事
实进行有关计算和作图.
1.观察有横格线的练习簿页(如图),这些横格线有什么特征?在图中任意画几条直线,使之与横格线相交.这些横格线在每一条所画的直线上截得的线段有什么规律?
合作学习
2.观察下图.
l1,l2,l3,
l4,l5是一组等距离的平行线.
AE与A'E'是任意画的两条直线,分别与这组平行线依次相交于点A,B,C,D,E和A',B',C',D',E'.
比例式
=
成立吗?
=
呢?
=
呢?
为什么?你还能再找出两组比例线段吗?
我们有以下的基本事实:
两条直线被一组平行线(不少于3条)所截,所得的对应线段成比例.
获取新知
1.基本事实
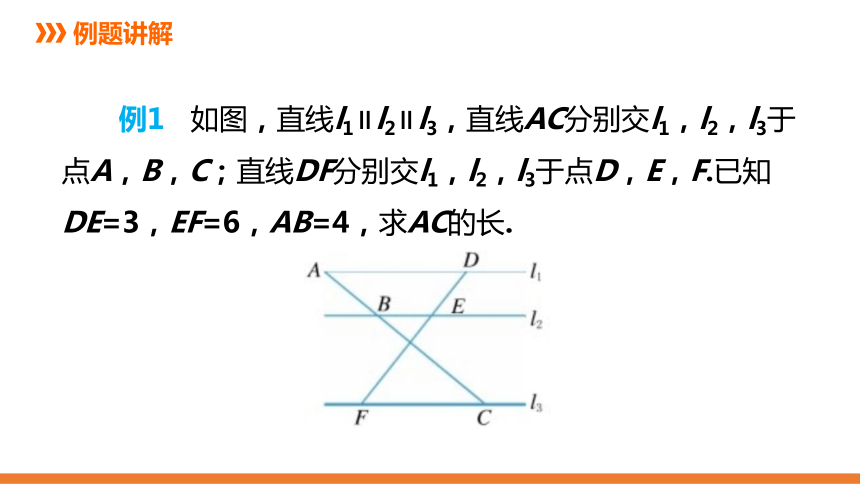
例1
如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D,E,F.已知DE=3,EF=6,AB=4,求AC的长.
例题讲解
解:∵
l1∥l2∥l3
,
∴
=
(两条直线被一组平行线所截,所得的对应线段成比例),
∴
=
,
解得AC=12.
点评:利用平行线分线段定理求线段的长.
【归纳总结】
想一想
若要把一条线段二等分,除了作线段的中垂线之外,
你还有什么方法?如果要三等分呢?
例2
已知线段AB(如图).把线段AB五等分.
接下来我们一起来看一下面的问题.
作法
如图.
1.以A为端点作一条射线,并在射线上依次截取线段AA1=A1A2=A2A3=A3A4,=A4A5.
2.连结A5B,并过点A1,A2,A3,A4分别作A5B的平行线,依次交AB于点B1,B2,B3,B4.
点B1,B2,B3,B4就是所
求作的把线段AB五等分的点.
总结:通过本题学习,我们
可以将线段任意等分.
事实上,我们只要过点A作一条与A5B平行的直线l(如图),就可以根据“两条直线被一组平行线所截,所得的对应线段成比例”的基本事实,得到:
=
=
=
=
.
而AA1=A1A2=A2A3=A3A4=A4A5,
∴AB1=B1B2=B2B3=B3B4=B4B,
这就证明了点B1,B2,B3,B4是所求作的分点.
想一想
把线段AB分成AC,CB两条线段,并使AC∶CB=2∶3,应怎么作?
图
4
点评:本题考查的是平行线分线段成比
例定理的应用,正确作出辅助线、灵活运
用定理、找准对应关系是解题的关键.
【归纳总结】利用平行线分线段成比例证明比例式(等积式)成立的方法
(1)构建平行关系:在三角形中通常过某一点作某一边或重要线段的平行线;
(2)列比例式:根据平行线分线段成比例基本事实列出比例式;
(3)比例式变形:根据比例的基本性质将比例式变形.
C
图1
随堂演练
图2
B
图3
图4-2-3
4.如图4-2-3,已知AB∥CD∥EF,且BE与AF交于点O,AD=3,BC=2,CE=1.5,求AF的长.
图5
证明:∵EF∥CD,∴
又∵DE∥BC,
∴
∴
∴AD是AF与AB的比例中项.
成比例
课堂小结
作业:
同步课时作业
第4章
相似三角形
4.2
由平行线截得的比例线段
你能用直尺和圆规把一条线段三等分吗?
情景导入
学习目标
1.经历基本事实:两条直线被一组平行线
(不少3条)所截,所得的对应线段成比
例的发现过程.
2.掌握上述基本事实,会运用上述基本事
实进行有关计算和作图.
1.观察有横格线的练习簿页(如图),这些横格线有什么特征?在图中任意画几条直线,使之与横格线相交.这些横格线在每一条所画的直线上截得的线段有什么规律?
合作学习
2.观察下图.
l1,l2,l3,
l4,l5是一组等距离的平行线.
AE与A'E'是任意画的两条直线,分别与这组平行线依次相交于点A,B,C,D,E和A',B',C',D',E'.
比例式
=
成立吗?
=
呢?
=
呢?
为什么?你还能再找出两组比例线段吗?
我们有以下的基本事实:
两条直线被一组平行线(不少于3条)所截,所得的对应线段成比例.
获取新知
1.基本事实
例1
如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D,E,F.已知DE=3,EF=6,AB=4,求AC的长.
例题讲解
解:∵
l1∥l2∥l3
,
∴
=
(两条直线被一组平行线所截,所得的对应线段成比例),
∴
=
,
解得AC=12.
点评:利用平行线分线段定理求线段的长.
【归纳总结】
想一想
若要把一条线段二等分,除了作线段的中垂线之外,
你还有什么方法?如果要三等分呢?
例2
已知线段AB(如图).把线段AB五等分.
接下来我们一起来看一下面的问题.
作法
如图.
1.以A为端点作一条射线,并在射线上依次截取线段AA1=A1A2=A2A3=A3A4,=A4A5.
2.连结A5B,并过点A1,A2,A3,A4分别作A5B的平行线,依次交AB于点B1,B2,B3,B4.
点B1,B2,B3,B4就是所
求作的把线段AB五等分的点.
总结:通过本题学习,我们
可以将线段任意等分.
事实上,我们只要过点A作一条与A5B平行的直线l(如图),就可以根据“两条直线被一组平行线所截,所得的对应线段成比例”的基本事实,得到:
=
=
=
=
.
而AA1=A1A2=A2A3=A3A4=A4A5,
∴AB1=B1B2=B2B3=B3B4=B4B,
这就证明了点B1,B2,B3,B4是所求作的分点.
想一想
把线段AB分成AC,CB两条线段,并使AC∶CB=2∶3,应怎么作?
图
4
点评:本题考查的是平行线分线段成比
例定理的应用,正确作出辅助线、灵活运
用定理、找准对应关系是解题的关键.
【归纳总结】利用平行线分线段成比例证明比例式(等积式)成立的方法
(1)构建平行关系:在三角形中通常过某一点作某一边或重要线段的平行线;
(2)列比例式:根据平行线分线段成比例基本事实列出比例式;
(3)比例式变形:根据比例的基本性质将比例式变形.
C
图1
随堂演练
图2
B
图3
图4-2-3
4.如图4-2-3,已知AB∥CD∥EF,且BE与AF交于点O,AD=3,BC=2,CE=1.5,求AF的长.
图5
证明:∵EF∥CD,∴
又∵DE∥BC,
∴
∴
∴AD是AF与AB的比例中项.
成比例
课堂小结
作业:
同步课时作业
同课章节目录
