4.4 两个相似三角形的判定 课件(共17张PPT)
文档属性
| 名称 | 4.4 两个相似三角形的判定 课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 953.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-20 14:10:38 | ||
图片预览

文档简介
(共17张PPT)
4.4两个相似三角形的判定(3)
新知导入
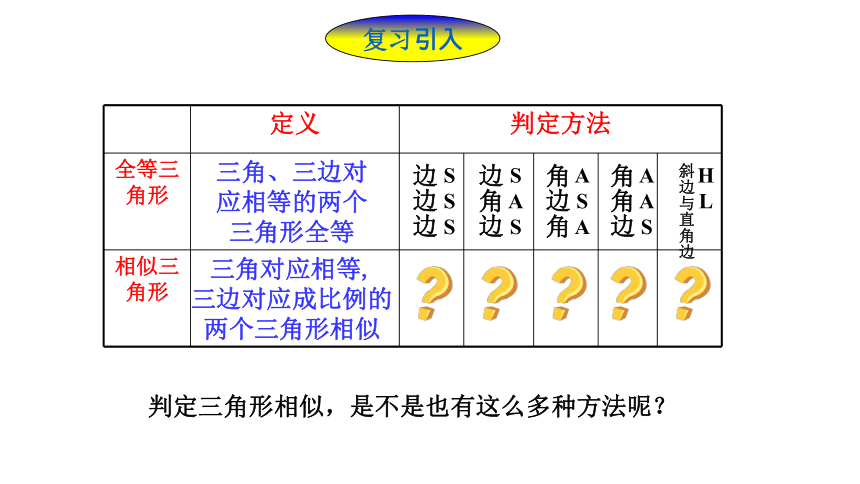
复习引入
定义
判定方法
全等三角形
相似三角形
三角、三边对应相等的两个三角形全等
三角对应相等,
三边对应成比例的两个三角形相似
角边角
A
S
A
角角边
A
A
S
边边边
S
S
S
边角边
S
A
S
斜边与直角边
H
L
判定三角形相似,是不是也有这么多种方法呢?
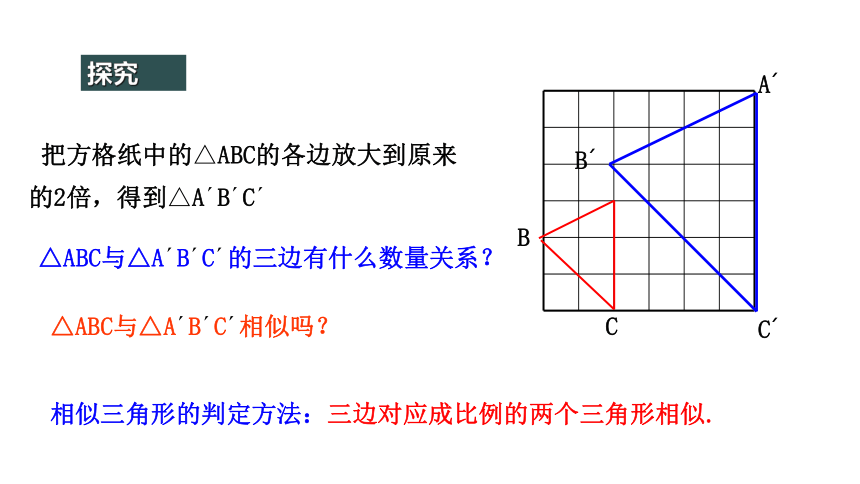
探究
把方格纸中的△ABC的各边放大到原来的2倍,得到△A?B?C?
△ABC与△A?B?C?相似吗?
△ABC与△A?B?C?的三边有什么数量关系?
相似三角形的判定方法:三边对应成比例的两个三角形相似.
B
C
A?
C?
B?
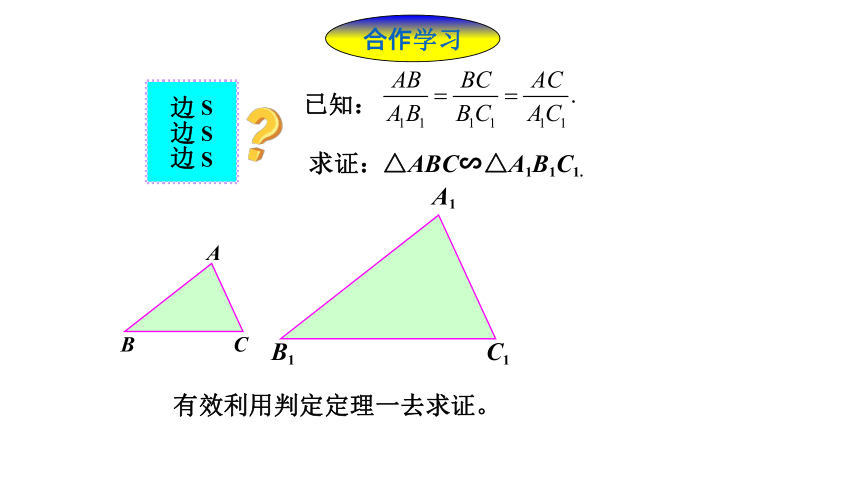
合作学习
边边边
S
S
S
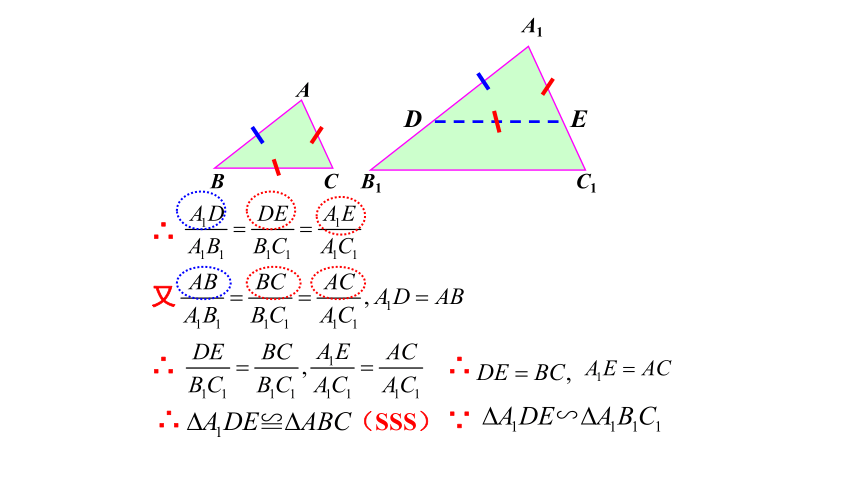
已知:
A1
B1
C1
A
B
C
求证:
有效利用判定定理一去求证。
△ABC∽△A1B1C1.
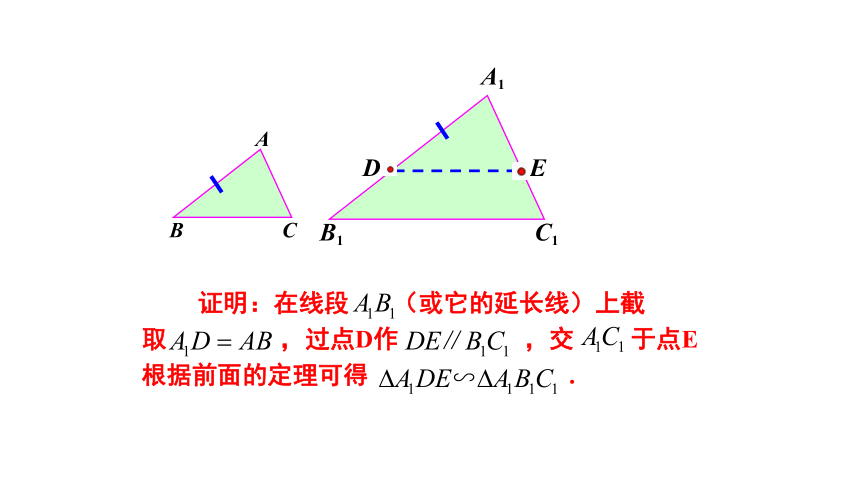
证明:在线段
(或它的延长线)上截取
,过点D作
,交
于点E根据前面的定理可得
.
A1
B1
C1
A
B
C
D
E
∴
又
A1
B1
C1
A
B
C
D
E
∴
∴
∴
(SSS)
∵
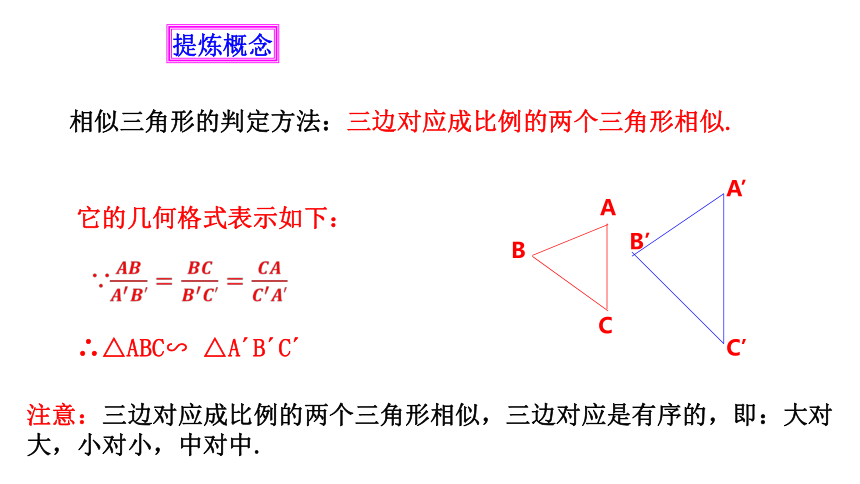
提炼概念
相似三角形的判定方法:三边对应成比例的两个三角形相似.
它的几何格式表示如下:
∴△ABC∽
△A?B?C?
?
注意:三边对应成比例的两个三角形相似,三边对应是有序的,即:大对大,小对小,中对中.
A
B
C
A’
C’
B’
全等判定
相似三角形的判定
ASA
AAS
(AA)有两个角对应相等的两个三角形相似
SAS
两边对应成比例,且夹角相等的两个三角形相似
SSS
三边对应成比例的两个三角形相似
典例精讲
解:观察图形根据勾股定理我们可以计算出
?
?
∴△ABC∽△EFD
例4
如图,判断4×4方格中的两个三角形是否相似,并说明理由.
例5
已知:如图,O为△ABC内一点,
分别是OA,OB,OC上的点,且
.
求证:
∽△ABC
.
证明:在△OA’B’与△OAB中,
?
∴△OA’B’∽△OAB,
?
?
?
?
?
∴△A’B’C’
∽△ABC
课堂练习
(1)所有的等腰三角形都相似。
(2)所有的等腰直角三角形都相似。
(3)所有的等边三角形都相似。
1.
判断下列说法是否正确?并说明理由。
√
×
√
2.如图,将方格纸分成6个三角形,在②,③,④,⑤,⑥5个三角形中,与三角形①相似的三角形有______.
③
3.如图,在矩形ABEF中,四边形ABCH、四边形CDGH和四边形DEFG都是正方形,图中的△ACD与△ECA相似吗?为什么?
课堂小结
三角形相似的判定方法
定理3:三边对应成比例的两个三角形相似.
注意:三边对应成比例的两个三角形相似,三边对应是有序的,即:大对大,小对小,中对中.
4.4两个相似三角形的判定(3)
新知导入
复习引入
定义
判定方法
全等三角形
相似三角形
三角、三边对应相等的两个三角形全等
三角对应相等,
三边对应成比例的两个三角形相似
角边角
A
S
A
角角边
A
A
S
边边边
S
S
S
边角边
S
A
S
斜边与直角边
H
L
判定三角形相似,是不是也有这么多种方法呢?
探究
把方格纸中的△ABC的各边放大到原来的2倍,得到△A?B?C?
△ABC与△A?B?C?相似吗?
△ABC与△A?B?C?的三边有什么数量关系?
相似三角形的判定方法:三边对应成比例的两个三角形相似.
B
C
A?
C?
B?
合作学习
边边边
S
S
S
已知:
A1
B1
C1
A
B
C
求证:
有效利用判定定理一去求证。
△ABC∽△A1B1C1.
证明:在线段
(或它的延长线)上截取
,过点D作
,交
于点E根据前面的定理可得
.
A1
B1
C1
A
B
C
D
E
∴
又
A1
B1
C1
A
B
C
D
E
∴
∴
∴
(SSS)
∵
提炼概念
相似三角形的判定方法:三边对应成比例的两个三角形相似.
它的几何格式表示如下:
∴△ABC∽
△A?B?C?
?
注意:三边对应成比例的两个三角形相似,三边对应是有序的,即:大对大,小对小,中对中.
A
B
C
A’
C’
B’
全等判定
相似三角形的判定
ASA
AAS
(AA)有两个角对应相等的两个三角形相似
SAS
两边对应成比例,且夹角相等的两个三角形相似
SSS
三边对应成比例的两个三角形相似
典例精讲
解:观察图形根据勾股定理我们可以计算出
?
?
∴△ABC∽△EFD
例4
如图,判断4×4方格中的两个三角形是否相似,并说明理由.
例5
已知:如图,O为△ABC内一点,
分别是OA,OB,OC上的点,且
.
求证:
∽△ABC
.
证明:在△OA’B’与△OAB中,
?
∴△OA’B’∽△OAB,
?
?
?
?
?
∴△A’B’C’
∽△ABC
课堂练习
(1)所有的等腰三角形都相似。
(2)所有的等腰直角三角形都相似。
(3)所有的等边三角形都相似。
1.
判断下列说法是否正确?并说明理由。
√
×
√
2.如图,将方格纸分成6个三角形,在②,③,④,⑤,⑥5个三角形中,与三角形①相似的三角形有______.
③
3.如图,在矩形ABEF中,四边形ABCH、四边形CDGH和四边形DEFG都是正方形,图中的△ACD与△ECA相似吗?为什么?
课堂小结
三角形相似的判定方法
定理3:三边对应成比例的两个三角形相似.
注意:三边对应成比例的两个三角形相似,三边对应是有序的,即:大对大,小对小,中对中.
同课章节目录
