浙教版九年级数学上册 4.6相似多边形课件(19张ppt)
文档属性
| 名称 | 浙教版九年级数学上册 4.6相似多边形课件(19张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 369.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 08:23:23 | ||
图片预览



文档简介
(共19张PPT)
相似多边形
学习目标
掌握
1.掌握相似多边形的概念.
2.掌握相似多边形的性质.
A
B
C
D
A1
B1
C1
D1
如图:四边形A1B1C1D1是四边形ABCD经过相似变换所得的像,
请分别求出这两个四边形的对应边的长度,并分别量出这两个四边形各个内角的度数,
然后与你的同伴议一议;这两个四边形的对应角之间有什么关系?对应边之间有什么关系?
各对应角相等、各对应边成比例的两个多边形叫做相似多边形.
相似多边形对应边的比叫做相似比.
相似多边形
相似比
对应顶点的字母写在对应的位置上
如果两个多边形相似,那么它们的对应角有什么关系?对应边呢?
相似多边形的对应角相等,对应边成比例.
相似多边形的性质
相似多边形的周长之比等于相似比;面积之比等于相似比的平方.
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
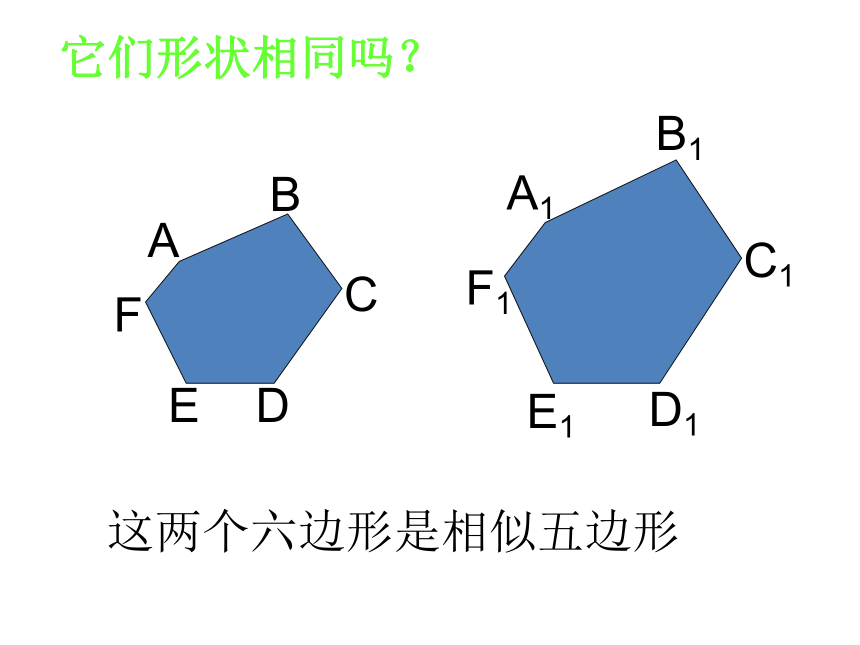
它们形状相同吗?
这两个六边形是相似五边形
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
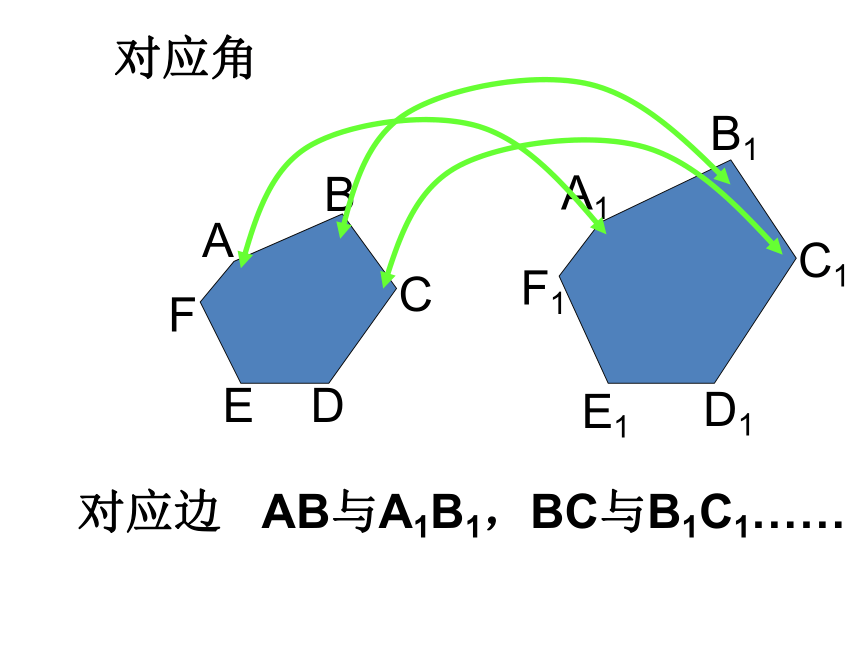
对应角
对应边
AB与A1B1,BC与B1C1……
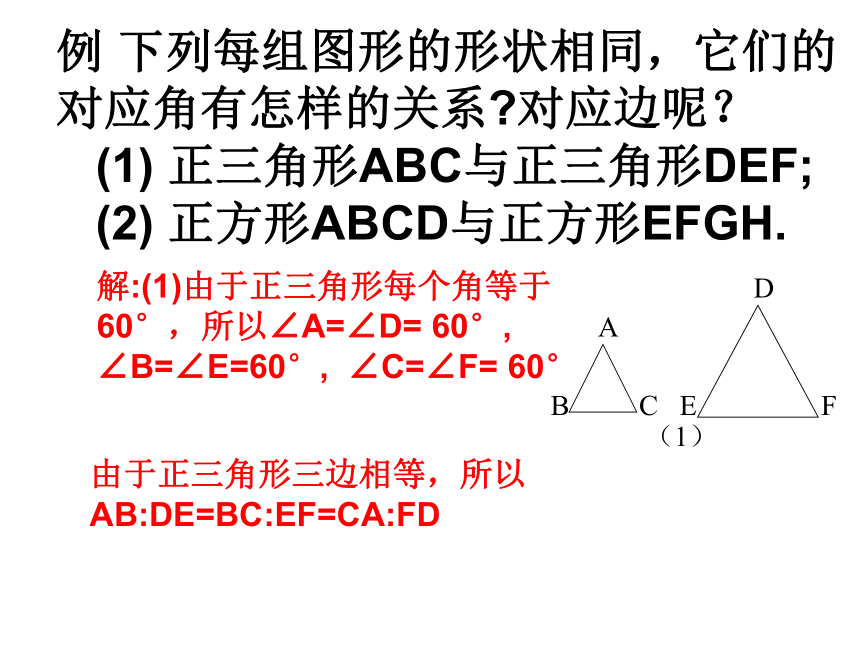
例
下列每组图形的形状相同,它们的对应角有怎样的关系?对应边呢?
(1)
正三角形ABC与正三角形DEF;
(2)
正方形ABCD与正方形EFGH.
解:(1)由于正三角形每个角等于60°,所以∠A=∠D=
60°,
∠B=∠E=60°,
∠C=∠F=
60°
由于正三角形三边相等,所以
AB:DE=BC:EF=CA:FD
(1)
B
C
D
E
F
A
解:(2)、由于正方形的每个角都是直角,所以
∠A=∠E=
90°
∠B=∠F=90°
∠C=∠G=
90°
∠D=∠H=
90°
由于正方形的四边相等,所以
AB:EF=BC:FG=CD:GH=DA:HE
A
B
E
G
D
C
F
H
议一议
正方形
10
10
菱形
12
12
它们相似吗?
正方形
10
10
矩形
12
8
它们呢?
书本151页课内练习
比一比,赛一赛
1.(知识点1)下列说法中,错误的是
(
)
A.正六边形都相似
B.等腰直角三角形都相似
C.矩形都相似
D.正方形都相似
2.(知识点2)两个相似多边形的面积之比为1∶3,则它们周长之比为
(
)
A.1∶3 B.1∶9
【对点自测】
C
C
3.(知识点2)在比例尺为1∶10
000的地图上,若某物在图上的面积为50
cm2,则该物实际面积为
(
)
A.50
m2
B.5
000
m2
C.50
000
m2
D.500
000
m2
4.(知识点2)一个多边形的边长分别为2,3,4,5,6,另一个和它相似的多边形的最短边长为6,则这个多边形的最长边是
(
)
A.12
B.18
C.24
D.30
D
B
课堂作业
1、右面两个矩形相似,求它们对应边的比.
2、如图,两个正六边形的边长分别为a和b,它们相似吗?为什么?
如图,矩形的草坪长20m,宽10m,沿草坪四周外围有1m的环行小路,小路的内外边缘所成的矩形相似吗?
2
3
2∶3
相似.理由是:各对应角相等,各对应边成比例.
不相似.因为对应边不成比例.
1.
E,F分别为矩形ABCD的边AD,BC的中点,若矩形ABCD∽矩形EABF,AB=2,则矩形ABCD的面积为
(
)
图4-6-6
A.1
B.2
C
2.如图4-6-7,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a,b应满足的条件是
(
)
B
图4-6-7
A
B
C
D
E
F
2
例:矩形纸张的长与宽的比为
,对开后所得的矩形纸张是否与原来的矩形纸相似?请说明理由.
解:对开后所得的矩形纸张和原来的矩形纸张相似,理由如下:设原来的纸张为矩形ABCD,如图:
连结BC与AD的中点F,E,则EF就把矩形ABCD分为全等的两个矩形.
在矩形ABCD中,
矩形ABFE与矩形BCDA的对应角相等,对应边成比例,矩形ABFE与矩形BCDA相似
可以发现,这些叠放起来的矩形的右上顶点同在一直线上,这是因为这些小矩形都是相似的,所以它们的长与宽对应成比例,
0
(2)
如果以图(2)最大矩形的左下顶点为原点,宽和长所在直线分别为x轴、y轴,
把标准纸(长与宽之比为 )一次又一次对开如右图叠起来,你发现了什么有趣的现象?你能给出数学解释吗?
探究活动
2
那么这组矩形右上顶点的坐标都满足
两个相似多边形的一对对应边的边分别是15
cm和12
cm.
(1)它们的周长相差24
cm,求这两个多边形的周长;
(2)它们的面积相差270
cm2,求这两个多边形的面积.
?解:(1)设较大多边形的周长是x
cm.则x∶(x-24)=5∶4,
解得x=120,∴较小多边形的周长为120-24=96(cm);
(2)设较大多边形的面积为a
cm2,由题意得:
a∶(a-270)=25∶16,解得a=750,
则较小多边形的面积为750-270=480(cm2).
今天我们了解了相似图形王国的一个伟大的家族……
相似多边形
相似多边形的对应角相等,对应边成比例.
相似多边形的性质
谈谈收获
相似多边形的周长之比等于相似比;
面积之比等于相似比的平方.
相似多边形
学习目标
掌握
1.掌握相似多边形的概念.
2.掌握相似多边形的性质.
A
B
C
D
A1
B1
C1
D1
如图:四边形A1B1C1D1是四边形ABCD经过相似变换所得的像,
请分别求出这两个四边形的对应边的长度,并分别量出这两个四边形各个内角的度数,
然后与你的同伴议一议;这两个四边形的对应角之间有什么关系?对应边之间有什么关系?
各对应角相等、各对应边成比例的两个多边形叫做相似多边形.
相似多边形对应边的比叫做相似比.
相似多边形
相似比
对应顶点的字母写在对应的位置上
如果两个多边形相似,那么它们的对应角有什么关系?对应边呢?
相似多边形的对应角相等,对应边成比例.
相似多边形的性质
相似多边形的周长之比等于相似比;面积之比等于相似比的平方.
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
它们形状相同吗?
这两个六边形是相似五边形
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
对应角
对应边
AB与A1B1,BC与B1C1……
例
下列每组图形的形状相同,它们的对应角有怎样的关系?对应边呢?
(1)
正三角形ABC与正三角形DEF;
(2)
正方形ABCD与正方形EFGH.
解:(1)由于正三角形每个角等于60°,所以∠A=∠D=
60°,
∠B=∠E=60°,
∠C=∠F=
60°
由于正三角形三边相等,所以
AB:DE=BC:EF=CA:FD
(1)
B
C
D
E
F
A
解:(2)、由于正方形的每个角都是直角,所以
∠A=∠E=
90°
∠B=∠F=90°
∠C=∠G=
90°
∠D=∠H=
90°
由于正方形的四边相等,所以
AB:EF=BC:FG=CD:GH=DA:HE
A
B
E
G
D
C
F
H
议一议
正方形
10
10
菱形
12
12
它们相似吗?
正方形
10
10
矩形
12
8
它们呢?
书本151页课内练习
比一比,赛一赛
1.(知识点1)下列说法中,错误的是
(
)
A.正六边形都相似
B.等腰直角三角形都相似
C.矩形都相似
D.正方形都相似
2.(知识点2)两个相似多边形的面积之比为1∶3,则它们周长之比为
(
)
A.1∶3 B.1∶9
【对点自测】
C
C
3.(知识点2)在比例尺为1∶10
000的地图上,若某物在图上的面积为50
cm2,则该物实际面积为
(
)
A.50
m2
B.5
000
m2
C.50
000
m2
D.500
000
m2
4.(知识点2)一个多边形的边长分别为2,3,4,5,6,另一个和它相似的多边形的最短边长为6,则这个多边形的最长边是
(
)
A.12
B.18
C.24
D.30
D
B
课堂作业
1、右面两个矩形相似,求它们对应边的比.
2、如图,两个正六边形的边长分别为a和b,它们相似吗?为什么?
如图,矩形的草坪长20m,宽10m,沿草坪四周外围有1m的环行小路,小路的内外边缘所成的矩形相似吗?
2
3
2∶3
相似.理由是:各对应角相等,各对应边成比例.
不相似.因为对应边不成比例.
1.
E,F分别为矩形ABCD的边AD,BC的中点,若矩形ABCD∽矩形EABF,AB=2,则矩形ABCD的面积为
(
)
图4-6-6
A.1
B.2
C
2.如图4-6-7,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a,b应满足的条件是
(
)
B
图4-6-7
A
B
C
D
E
F
2
例:矩形纸张的长与宽的比为
,对开后所得的矩形纸张是否与原来的矩形纸相似?请说明理由.
解:对开后所得的矩形纸张和原来的矩形纸张相似,理由如下:设原来的纸张为矩形ABCD,如图:
连结BC与AD的中点F,E,则EF就把矩形ABCD分为全等的两个矩形.
在矩形ABCD中,
矩形ABFE与矩形BCDA的对应角相等,对应边成比例,矩形ABFE与矩形BCDA相似
可以发现,这些叠放起来的矩形的右上顶点同在一直线上,这是因为这些小矩形都是相似的,所以它们的长与宽对应成比例,
0
(2)
如果以图(2)最大矩形的左下顶点为原点,宽和长所在直线分别为x轴、y轴,
把标准纸(长与宽之比为 )一次又一次对开如右图叠起来,你发现了什么有趣的现象?你能给出数学解释吗?
探究活动
2
那么这组矩形右上顶点的坐标都满足
两个相似多边形的一对对应边的边分别是15
cm和12
cm.
(1)它们的周长相差24
cm,求这两个多边形的周长;
(2)它们的面积相差270
cm2,求这两个多边形的面积.
?解:(1)设较大多边形的周长是x
cm.则x∶(x-24)=5∶4,
解得x=120,∴较小多边形的周长为120-24=96(cm);
(2)设较大多边形的面积为a
cm2,由题意得:
a∶(a-270)=25∶16,解得a=750,
则较小多边形的面积为750-270=480(cm2).
今天我们了解了相似图形王国的一个伟大的家族……
相似多边形
相似多边形的对应角相等,对应边成比例.
相似多边形的性质
谈谈收获
相似多边形的周长之比等于相似比;
面积之比等于相似比的平方.
同课章节目录
