4.7 图形的位似 同步课件(27张ppt)
文档属性
| 名称 | 4.7 图形的位似 同步课件(27张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-20 14:04:35 | ||
图片预览





文档简介
(共27张PPT)
第4章
相似三角形
4.7
图形的位似
观察思考:这两幅图片有什么特征?
答:都是有好几张相似图形组成,每个对应顶点都在同一个端点出发的射线上。
情景导入
学习目标
1.了解位似图形的概念.
2.了解位似图形的性质和以坐标原点为位似中心的
图形位似的性质.
3.能利用位似将一个图形放大或缩小.
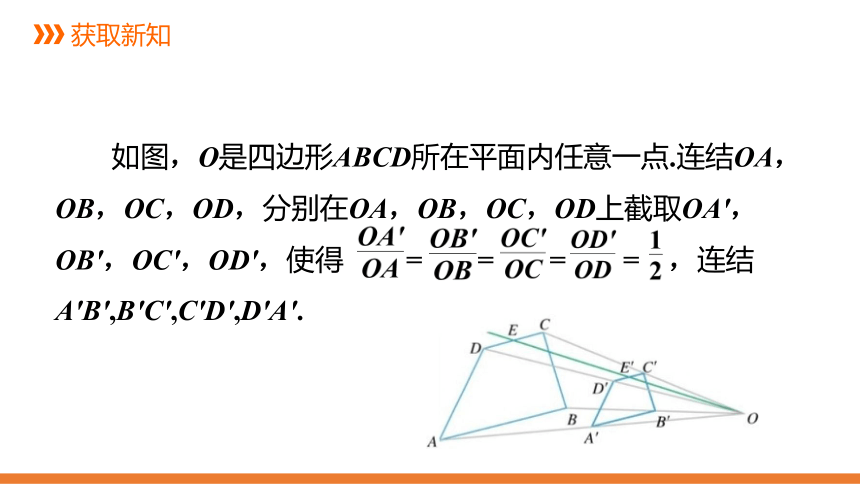
如图,O是四边形ABCD所在平面内任意一点.连结OA,OB,OC,OD,分别在OA,OB,OC,OD上截取OA',OB',OC',OD',使得
=
=
=
=
,连结A'B',B'C',C'D',D'A'.
获取新知
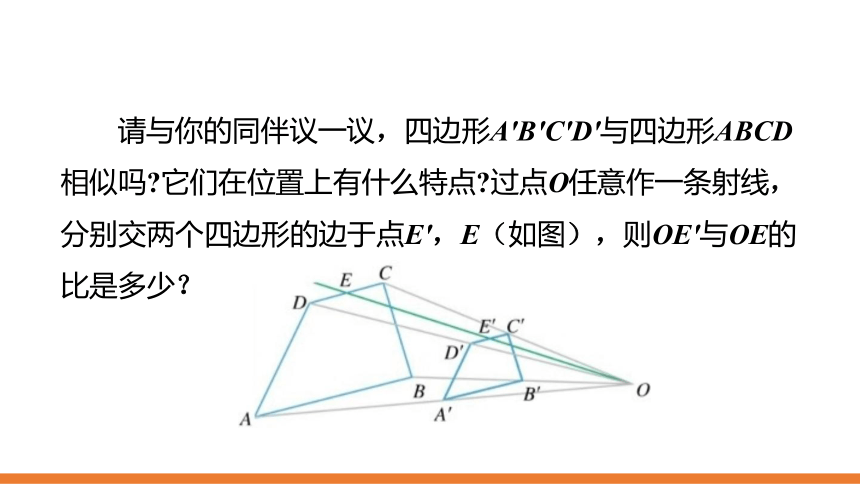
请与你的同伴议一议,四边形A'B'C'D'与四边形ABCD相似吗?它们在位置上有什么特点?过点O任意作一条射线,分别交两个四边形的边于点E',E(如图),则OE'与OE的比是多少?
一般地,如果两个图形满足以下两个条件:所有经过对应点的直线都相交于同一点;这个交点到两个对应点的距离之比都相等,那么这两个图形就叫做位似图形(homothetic
figures),经过各对应两点的直线的交点叫做位似中心(homothetic
centre).位似中心到两个对应点的距离之比叫做位似比(homothetic
ratio).
1.位似图形的概念
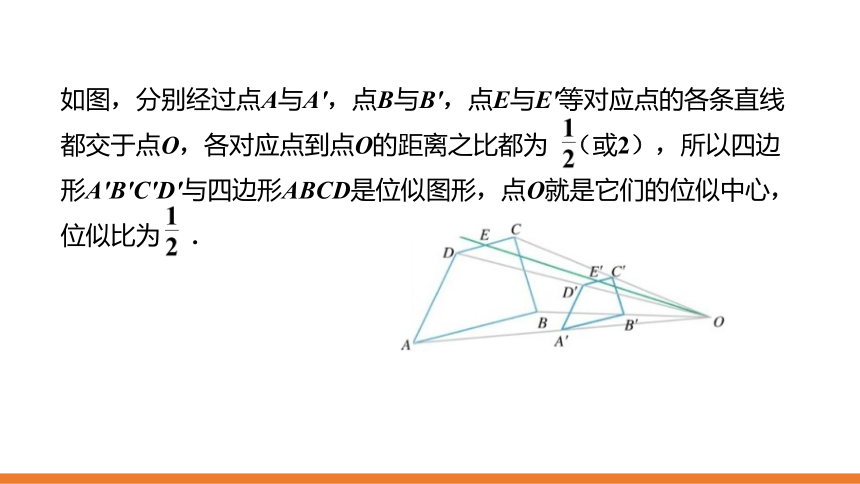
如图,分别经过点A与A',点B与B',点E与E'等对应点的各条直线都交于点O,各对应点到点O的距离之比都为
(或2),所以四边形A'B'C'D'与四边形ABCD是位似图形,点O就是它们的位似中心,位似比为
.
从图中还可以看到,位似多边形必定是相似多边形,
位似比也就是相似比.
2.位似图形的性质
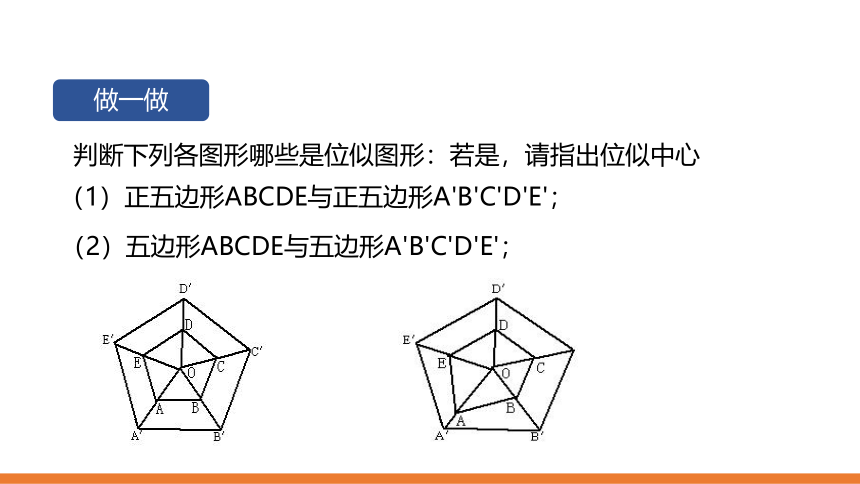
判断下列各图形哪些是位似图形:若是,请指出位似中心
(1)正五边形ABCDE与正五边形A'B'C'D'E';
(2)五边形ABCDE与五边形A'B'C'D'E';
做一做
(3)正方形ABCD∽正方形A'B'C'D'
(4)等边三角形ABC与等边三角形A'B'C'
1.两图形相似.
同时满足下面两个条件的两个图形才叫做位似图形.两条件缺一不可.
2.每组对应点所在直线都经过同一点.
归纳总结
放缩尺是将图形进行放大或缩小的工具.如图,点O位置固定不变,在A,A'处装有画笔.当画笔A沿图形F运动时,画笔A'画出图形F',图形F'将图形F放大了.反之,图形F是图形F'的缩小图形.位似比可通过调节点B,D的位置来确定.
例1
如图,请以坐标原点O为位似中心,作
ABCD的位似图形,并把
ABCD的边长放大3倍.
例题讲解
分析
把
ABCD的边长放大3倍,即画一个与
ABCD的位似比为3:1的平行四边形.
作法
如图.
1.连结OA,OB,OC,OD.
2.分别延长OA,OB,OC,OD至G,C,E,F,使
=
=
=
=3.
3.依次连结GC,CE,EF,FG.
四边形GCEF就是所求作的四边形.
总结:通过作原图形中边的平行线,来确定
位似后得到的图形.
如果按同样比例,反向延长OA,OB,OC,OD,就得到四边形G'C'E'F',也是所求作的四边形.
四边形GCEF与四边形G'C'E'F'具有怎样的对称性?
想一想
2.画位似图形的一般步骤
(1)定点:确定位似中心.
(2)连线:分别连结位似中心与原图形中的关键点.
(3)作点:根据位似比,作出原图形中的关键点的对应点.
(4)构图:按照原图形的形状,顺次连结上述各对应点,得到放大或缩小后的图形.
利用图形的位似可以把一个图形放大或缩小.若所画图形与原图形的位似比大于1,则将图形放大;若所画图形与原图形的位似比小于1,则将原图形缩小.
比较下图中各对应点的坐标,我们不难发现以坐标原点为位似中心的位似图形有以下性质:
当以坐标原点为位似中心时,若原图形上点的坐标为(x,y),位似图形与原图形的位似比为k,则位似图形上的对应点的坐标为(kx,ky)或(-kx,-ky).
3.关于原点对称
随堂演练
2.如图4-7-2,已知O是坐标原点,B,C两点的坐标分别为(3,-1),(2,1).
(1)以点O为位似中心,在y轴的左侧将△OBC放大两倍(即新图形与原图形的相似比为2∶1),画出△OB′C′;
(2)分别写出B,C两点的对应点B′,C′的坐标;
(3)如果△OBC内部一点M的坐标为(x,y),
写出点M的对应点M′的坐标.
解:(1)如图,延长BO到点B′,使B′O=2BO,延长CO到点C′,使C′O=2CO,连结B′C′.
则△OB′C′即为△OBC的位似图形.
(2)观察可知B′(-6,2),C′(-4,-2).
(3)M′(-2x,-2y).
位似比
课堂小结
作业:
同步课时作业
第4章
相似三角形
4.7
图形的位似
观察思考:这两幅图片有什么特征?
答:都是有好几张相似图形组成,每个对应顶点都在同一个端点出发的射线上。
情景导入
学习目标
1.了解位似图形的概念.
2.了解位似图形的性质和以坐标原点为位似中心的
图形位似的性质.
3.能利用位似将一个图形放大或缩小.
如图,O是四边形ABCD所在平面内任意一点.连结OA,OB,OC,OD,分别在OA,OB,OC,OD上截取OA',OB',OC',OD',使得
=
=
=
=
,连结A'B',B'C',C'D',D'A'.
获取新知
请与你的同伴议一议,四边形A'B'C'D'与四边形ABCD相似吗?它们在位置上有什么特点?过点O任意作一条射线,分别交两个四边形的边于点E',E(如图),则OE'与OE的比是多少?
一般地,如果两个图形满足以下两个条件:所有经过对应点的直线都相交于同一点;这个交点到两个对应点的距离之比都相等,那么这两个图形就叫做位似图形(homothetic
figures),经过各对应两点的直线的交点叫做位似中心(homothetic
centre).位似中心到两个对应点的距离之比叫做位似比(homothetic
ratio).
1.位似图形的概念
如图,分别经过点A与A',点B与B',点E与E'等对应点的各条直线都交于点O,各对应点到点O的距离之比都为
(或2),所以四边形A'B'C'D'与四边形ABCD是位似图形,点O就是它们的位似中心,位似比为
.
从图中还可以看到,位似多边形必定是相似多边形,
位似比也就是相似比.
2.位似图形的性质
判断下列各图形哪些是位似图形:若是,请指出位似中心
(1)正五边形ABCDE与正五边形A'B'C'D'E';
(2)五边形ABCDE与五边形A'B'C'D'E';
做一做
(3)正方形ABCD∽正方形A'B'C'D'
(4)等边三角形ABC与等边三角形A'B'C'
1.两图形相似.
同时满足下面两个条件的两个图形才叫做位似图形.两条件缺一不可.
2.每组对应点所在直线都经过同一点.
归纳总结
放缩尺是将图形进行放大或缩小的工具.如图,点O位置固定不变,在A,A'处装有画笔.当画笔A沿图形F运动时,画笔A'画出图形F',图形F'将图形F放大了.反之,图形F是图形F'的缩小图形.位似比可通过调节点B,D的位置来确定.
例1
如图,请以坐标原点O为位似中心,作
ABCD的位似图形,并把
ABCD的边长放大3倍.
例题讲解
分析
把
ABCD的边长放大3倍,即画一个与
ABCD的位似比为3:1的平行四边形.
作法
如图.
1.连结OA,OB,OC,OD.
2.分别延长OA,OB,OC,OD至G,C,E,F,使
=
=
=
=3.
3.依次连结GC,CE,EF,FG.
四边形GCEF就是所求作的四边形.
总结:通过作原图形中边的平行线,来确定
位似后得到的图形.
如果按同样比例,反向延长OA,OB,OC,OD,就得到四边形G'C'E'F',也是所求作的四边形.
四边形GCEF与四边形G'C'E'F'具有怎样的对称性?
想一想
2.画位似图形的一般步骤
(1)定点:确定位似中心.
(2)连线:分别连结位似中心与原图形中的关键点.
(3)作点:根据位似比,作出原图形中的关键点的对应点.
(4)构图:按照原图形的形状,顺次连结上述各对应点,得到放大或缩小后的图形.
利用图形的位似可以把一个图形放大或缩小.若所画图形与原图形的位似比大于1,则将图形放大;若所画图形与原图形的位似比小于1,则将原图形缩小.
比较下图中各对应点的坐标,我们不难发现以坐标原点为位似中心的位似图形有以下性质:
当以坐标原点为位似中心时,若原图形上点的坐标为(x,y),位似图形与原图形的位似比为k,则位似图形上的对应点的坐标为(kx,ky)或(-kx,-ky).
3.关于原点对称
随堂演练
2.如图4-7-2,已知O是坐标原点,B,C两点的坐标分别为(3,-1),(2,1).
(1)以点O为位似中心,在y轴的左侧将△OBC放大两倍(即新图形与原图形的相似比为2∶1),画出△OB′C′;
(2)分别写出B,C两点的对应点B′,C′的坐标;
(3)如果△OBC内部一点M的坐标为(x,y),
写出点M的对应点M′的坐标.
解:(1)如图,延长BO到点B′,使B′O=2BO,延长CO到点C′,使C′O=2CO,连结B′C′.
则△OB′C′即为△OBC的位似图形.
(2)观察可知B′(-6,2),C′(-4,-2).
(3)M′(-2x,-2y).
位似比
课堂小结
作业:
同步课时作业
同课章节目录
