3.6 圆内接四边形 课时练习(含答案)
文档属性
| 名称 | 3.6 圆内接四边形 课时练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 161.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-20 00:00:00 | ||
图片预览

文档简介
浙教版数学九年级上册
3.6《圆内接四边形》课时练习
一、选择题
1.如图,四边形
ABCD内接于⊙O,若∠BOD=100°,则∠DAB的度数为(?
)
?
?
A.50°??
???
B.80°??????????
C.100°????????
D.130°
2.如图,⊙O中,ABDC是圆内接四边形,∠BOC=110°,则∠BDC的度数是(???
)
A.110°
B.70°
C.55°
D.125°
3.如图,四边形ABCD内接于半圆O,已知∠ADC=140°,则∠AOC的大小是(??
)
A.40°??
?
?
B.60°??
??
?C.70°???
???
D.80°?
4.如图,在⊙O中,点A、B、C在⊙O上,且∠ACB=110°,则∠α=(??
)
A.70°???
B.110°?????
C.120°?????
D.140°
5.圆内接四边形ABCD,∠A,∠B,∠C的度数之比为3∶4∶6,则∠D的度数为( )
A.60°??
??
B.80°???
?
C.100°???
?
D.120°
6.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是( )
A.50°??????
B.60°??????
C.80°??????
D.100°
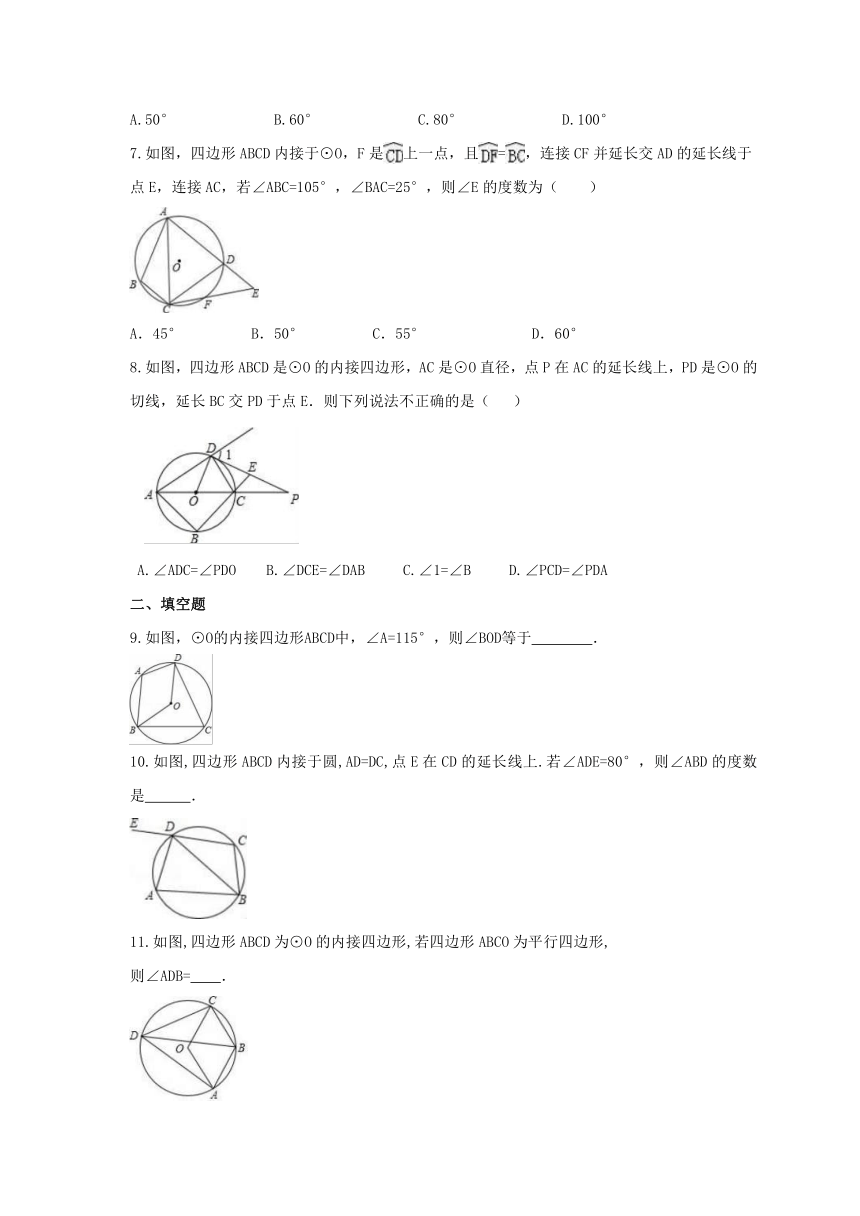
7.如图,四边形ABCD内接于⊙O,F是上一点,且=,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
A.45°
B.50°
C.55°
D.60°
8.如图,四边形ABCD是⊙O的内接四边形,AC是⊙O直径,点P在AC的延长线上,PD是⊙O的切线,延长BC交PD于点E.则下列说法不正确的是(
)
A.∠ADC=∠PDO
B.∠DCE=∠DAB
C.∠1=∠B
D.∠PCD=∠PDA
二、填空题
9.如图,⊙O的内接四边形ABCD中,∠A=115°,则∠BOD等于
.
10.如图,四边形ABCD内接于圆,AD=DC,点E在CD的延长线上.若∠ADE=80°,则∠ABD的度数是
.
11.如图,四边形ABCD为⊙O的内接四边形,若四边形ABCO为平行四边形,
则∠ADB=
.
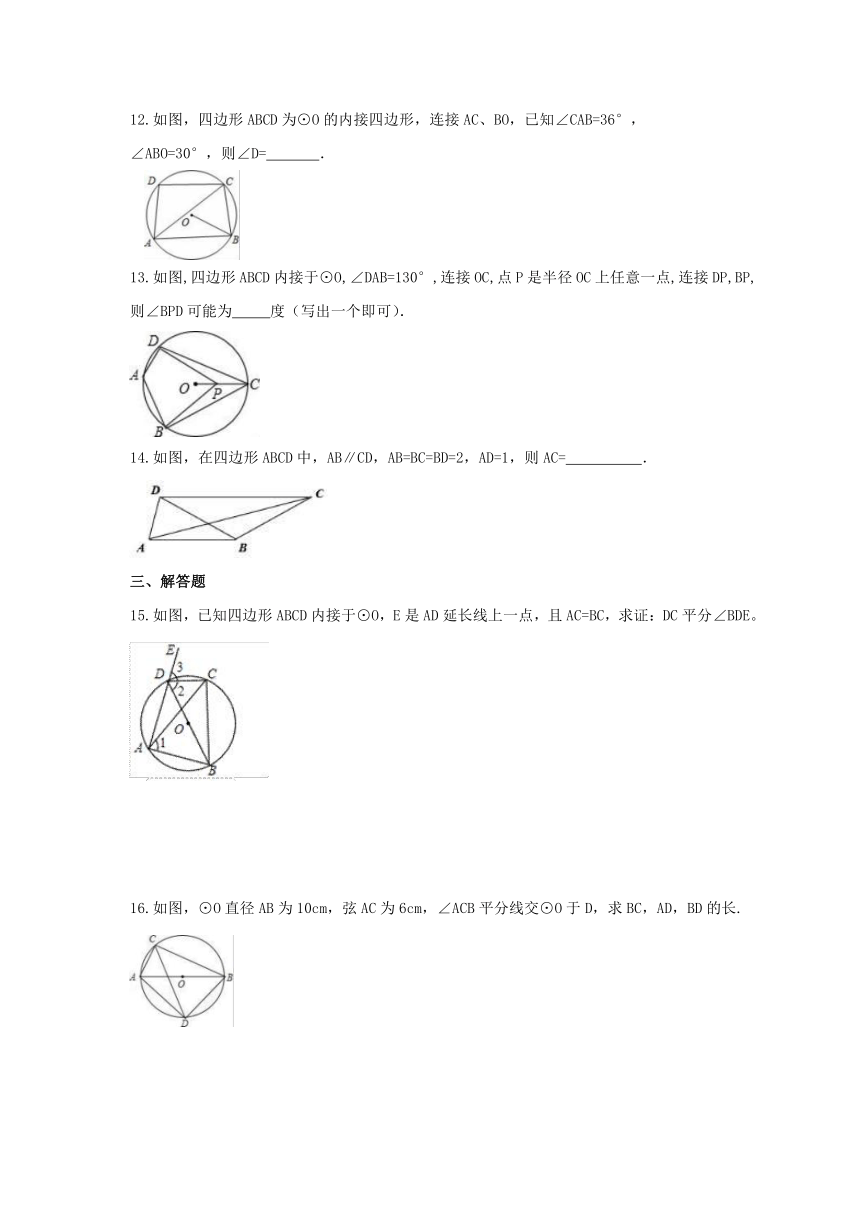
12.如图,四边形ABCD为⊙O的内接四边形,连接AC、BO,已知∠CAB=36°,
∠ABO=30°,则∠D=
.
13.如图,四边形ABCD内接于⊙O,∠DAB=130°,连接OC,点P是半径OC上任意一点,连接DP,BP,则∠BPD可能为
度(写出一个即可).
14.如图,在四边形ABCD中,AB∥CD,AB=BC=BD=2,AD=1,则AC=
.
三、解答题
15.如图,已知四边形ABCD内接于⊙O,E是AD延长线上一点,且AC=BC,求证:DC平分∠BDE。
16.如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB平分线交⊙O于D,求BC,AD,BD的长.
17.如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,
(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
参考答案
1.D
2.D?
3.D
4.D
5.C
6.D
7.B.
8.C
9.答案为:130°.
10.答案为:40°.
11.答案为:30°.
12.答案为:96.
13.答案为:80.
14.答案为:;
15.
16.解:∵AB是直径
∴∠ACB=∠ADB=90°
在Rt△ABC中,AB2=AC2+BC2,AB=10cm,AC=6cm
∴BC2=AB2﹣AC2=102﹣62=64
∴BC==8(cm)
又CD平分∠ACB,
∴∠ACD=∠BCD,
∴
∴AD=BD
又在Rt△ABD中,AD2+BD2=AB2
∴AD2+BD2=102
∴AD=BD==5(cm).
17.(1)证明:在△ABC中,
∵∠BAC=∠APC=60°,
又∵∠APC=∠ABC,
∴∠ABC=60°,
∴∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣60°﹣60°=60°,
∴△ABC是等边三角形;
(2)解:连接OB,
∵△ABC为等边三角形,⊙O为其外接圆,
∴O为△ABC的外心,
∴BO平分∠ABC,
∴∠OBD=30°,
∴OD=8×=4.
3.6《圆内接四边形》课时练习
一、选择题
1.如图,四边形
ABCD内接于⊙O,若∠BOD=100°,则∠DAB的度数为(?
)
?
?
A.50°??
???
B.80°??????????
C.100°????????
D.130°
2.如图,⊙O中,ABDC是圆内接四边形,∠BOC=110°,则∠BDC的度数是(???
)
A.110°
B.70°
C.55°
D.125°
3.如图,四边形ABCD内接于半圆O,已知∠ADC=140°,则∠AOC的大小是(??
)
A.40°??
?
?
B.60°??
??
?C.70°???
???
D.80°?
4.如图,在⊙O中,点A、B、C在⊙O上,且∠ACB=110°,则∠α=(??
)
A.70°???
B.110°?????
C.120°?????
D.140°
5.圆内接四边形ABCD,∠A,∠B,∠C的度数之比为3∶4∶6,则∠D的度数为( )
A.60°??
??
B.80°???
?
C.100°???
?
D.120°
6.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是( )
A.50°??????
B.60°??????
C.80°??????
D.100°
7.如图,四边形ABCD内接于⊙O,F是上一点,且=,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
A.45°
B.50°
C.55°
D.60°
8.如图,四边形ABCD是⊙O的内接四边形,AC是⊙O直径,点P在AC的延长线上,PD是⊙O的切线,延长BC交PD于点E.则下列说法不正确的是(
)
A.∠ADC=∠PDO
B.∠DCE=∠DAB
C.∠1=∠B
D.∠PCD=∠PDA
二、填空题
9.如图,⊙O的内接四边形ABCD中,∠A=115°,则∠BOD等于
.
10.如图,四边形ABCD内接于圆,AD=DC,点E在CD的延长线上.若∠ADE=80°,则∠ABD的度数是
.
11.如图,四边形ABCD为⊙O的内接四边形,若四边形ABCO为平行四边形,
则∠ADB=
.
12.如图,四边形ABCD为⊙O的内接四边形,连接AC、BO,已知∠CAB=36°,
∠ABO=30°,则∠D=
.
13.如图,四边形ABCD内接于⊙O,∠DAB=130°,连接OC,点P是半径OC上任意一点,连接DP,BP,则∠BPD可能为
度(写出一个即可).
14.如图,在四边形ABCD中,AB∥CD,AB=BC=BD=2,AD=1,则AC=
.
三、解答题
15.如图,已知四边形ABCD内接于⊙O,E是AD延长线上一点,且AC=BC,求证:DC平分∠BDE。
16.如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB平分线交⊙O于D,求BC,AD,BD的长.
17.如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,
(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
参考答案
1.D
2.D?
3.D
4.D
5.C
6.D
7.B.
8.C
9.答案为:130°.
10.答案为:40°.
11.答案为:30°.
12.答案为:96.
13.答案为:80.
14.答案为:;
15.
16.解:∵AB是直径
∴∠ACB=∠ADB=90°
在Rt△ABC中,AB2=AC2+BC2,AB=10cm,AC=6cm
∴BC2=AB2﹣AC2=102﹣62=64
∴BC==8(cm)
又CD平分∠ACB,
∴∠ACD=∠BCD,
∴
∴AD=BD
又在Rt△ABD中,AD2+BD2=AB2
∴AD2+BD2=102
∴AD=BD==5(cm).
17.(1)证明:在△ABC中,
∵∠BAC=∠APC=60°,
又∵∠APC=∠ABC,
∴∠ABC=60°,
∴∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣60°﹣60°=60°,
∴△ABC是等边三角形;
(2)解:连接OB,
∵△ABC为等边三角形,⊙O为其外接圆,
∴O为△ABC的外心,
∴BO平分∠ABC,
∴∠OBD=30°,
∴OD=8×=4.
同课章节目录
