浙教版初中数学八年级上 5.4 一次函数的图像 课件(17张ppt)
文档属性
| 名称 | 浙教版初中数学八年级上 5.4 一次函数的图像 课件(17张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-20 17:03:51 | ||
图片预览





文档简介
(共17张PPT)
5.4一次函数的图象(1)
情景
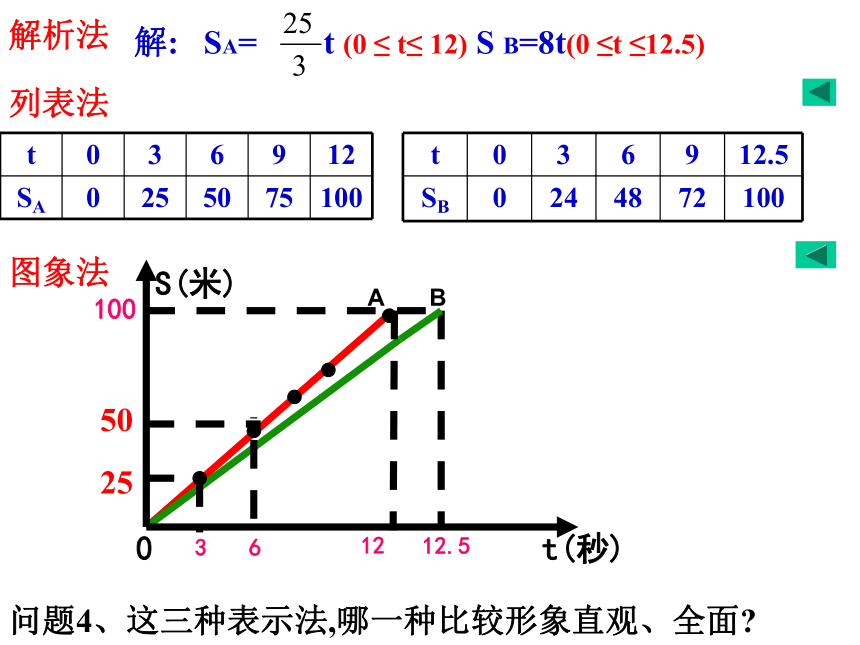
在校运会上,A同学和B同学参加了100米赛跑比赛,测得他们的平均速度是
米/秒和8米/秒,根据以下要求:表示他所跑的路程s与所用的时间t的函数关系.
问题1、这个关系能用解析法表示吗?能的话,请表示;
问题2、这个关系能用列表法表示吗?能的话,请表示;
把一个函数的自变量x的值与函数y的对应值分别作为点的横坐标和纵坐标,在直角坐标系中描出它的对应点,所有这些点组成的图形.叫做这个函数的图象。
问题3、(1)函数图象的概念:
(2)思考:根据概念,画一个函数图象需要几个步骤.
(3)
那么,你能用图象法来表示这个关系吗?能的话,画好图象,猜想图象是什么?
(1)取点; (2)描点;(3)连点
解析法
列表法
图象法
问题4、这三种表示法,哪一种比较形象直观、全面?
t
0
3
6
9
12
SA
0
25
50
75
100
解:
SA=
t
(0
≤
t≤
12)
S
B=8t(0
≤t
≤12.5)
t
0
3
6
9
12.5
SB
0
24
48
72
100
A
12.5
B
3
6
12
100
t(秒)
S(米)
0
25
50
1、列表:分别选取若干对自变量与函数的对应值,列成下表.
x
….
-2
-1
0
1
2
….
y=2x
….
….
y=2x+1
….
….
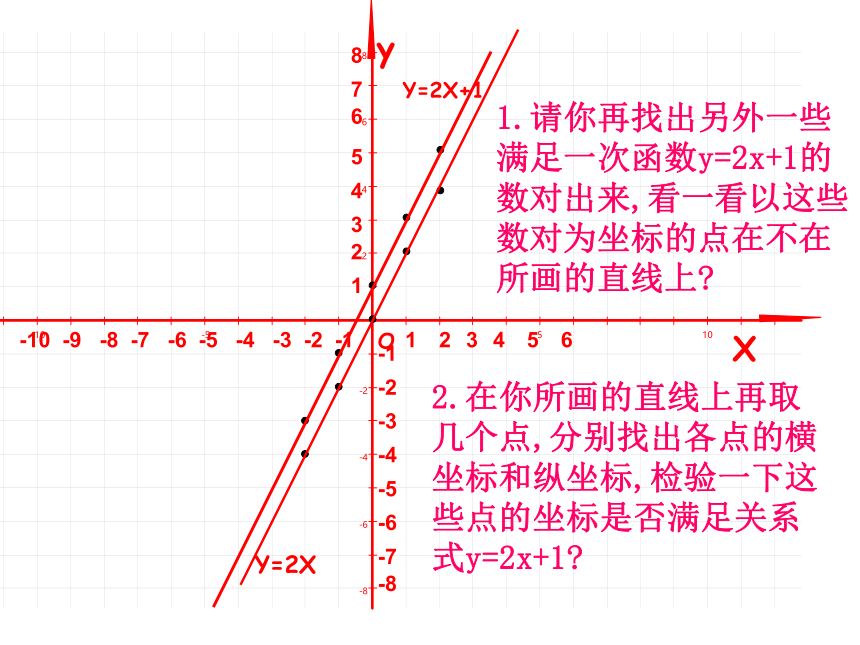
2、描点:在一个平面直角坐标系中,
描出这两组点.用光滑的线连接.
作出一次函数y=2x和Y=2X+1的图象
-4
-2
0
2
4
-3
-1
1
3
5
y
X
O
Y=2X
Y=2X+1
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
1
2
3
4
5
6
7
8
-7
-8
1.请你再找出另外一些满足一次函数y=2x+1的数对出来,看一看以这些数对为坐标的点在不在所画的直线上?
2.在你所画的直线上再取几个点,分别找出各点的横坐标和纵坐标,检验一下这些点的坐标是否满足关系式y=2x+1?
由此可见,一次函数Y=kx+b(k、b为常数,
k≠0
)可以用直角坐标系中的一条直线来表示,
从而这条直线就叫做一次函数Y=kx+b的图象.
所以,一次函数y=kx+b(k≠0)的图象也叫做直线y=kx+b
y
x
0
y=kx+b
2、函数图象的概念包含两个方面的内容:
(1)满足函数解析式的点,一定在这个函数图象上。
(2)反过来,在函数图象上的点的坐标满足函数的解析式。
3.(1)
点(2,9)在函数y=4x+1的图象上吗?
为什么?
(2)
点(-2,5)在函数y=4x+1的图象上吗?
为什么?
感悟:
1.若直线y=2x-3
经过点(1,a),
则a=_____
2.
已知点M(-3,
4)在直线y=
kx+1上,则k的值是__________
解:(1)把x=2代入函数,得y=4×2+1=9,
∴点(2,9)在函数
y=4x+1
的图象上
(2)把x=-2代入函数,得y=4×-2+1=-7≠5,
∴点(-2,5)不在函数y=4x+1的图象上
-1
-1
例1:在同一坐标系作出下列函数
的图象,并求它们与坐标轴的交点坐标.
Y=3x,
y=-3x+2
分析:因为一次函数的图象是一条直线,根据两点确定一条直线,只要画出图象上的两个点,就可以画出一次函数的图象.
对于函数y=3x,
取x=0,得y=0,得到点(0,0);取x=1,得y=3,得到点(1,3)
对于函数y=-3x+2,
取x=0,y=2,得到点(0,2);
取x=1,y=-1,得到点(1,-1)
在坐标系里描出各组点,分别过两点做直线就得到函数图象.
x
y
0
1
2
3
3
1
2
-1
-2
-2
-1
y=3x
y=-3x+2
100
t(秒)
S(米)
0
12.5
S=8t
(0≤t≤12.5)
以(0,0)、(12.5,100)为端点的一条线段.
经过(0,2)、(1,
-1)的一条直线
y=-3x+2
2
x
y
1
1
(1,-1)
.
y=-3x+2
(x<0)
y=-3x+2
(-1请描述下列函数的图象
以(-1,5)、(2,-4)为端点的线段,除(-1,5)外.
以(0,2)为端点,经过(-1,5)的射线,除(0,2)外
x
y
0
1
2
3
3
1
2
-1
-2
-2
-1
y=3x
y=-3x+2
(2)对于y=3x
当x=0时,y=0;当y=0时,x=0
∴和x轴、y轴的交点坐标都是(0,0)
当x=0时,y=2;
∴与y轴的交点坐标是(0,2),
当y=0时,x=
,
∴与x轴的交点坐标是(
,0)
(1)对于y=
-3x+2
直接利用函数解析式求
函数图象与坐标轴的交点坐标
求出一次函数与坐标轴的交点坐标
y=
–
3
x+2
y=3x
考考你
1.已知直线y=
-2x+4,它与x轴的交点为A,与y轴的交点为B.
(1).求A,
B两点的坐标.
(2).求?AOB的面积.
(O为坐标原点)
解:(1)取x=0,则y=4;
∴
B(0,4)
取y=0,则-2x+4=0,
解得x=2
∴A(2,0)
A
O
B
(2)∵AO=2
BO=4
∴S△AOB=?×2×4=4
2.一次函数的图象过M(3,2),N(-1,
-
6)
(1)求函数的解析式;
(2)试判断点P(2a,4a-4)是否在函数的图象上,并说明理由;
解:设函数解析式为y=kx+b
梳理一下吧!
2、函数图象的概念包含两个方面的内容:
(1)满足函数解析式的点一定在这个函数的图象上。
(2)在函数图象上的点的坐标一定满足函数解析式。
1、函数图象的概念:
把一个函数的自变量x与对应的函数y的值分别作
为点的横坐标和纵坐标
,
在直角坐标系内描出它的对
应点
,
所有这些点组成的图形叫做该函数的图象.
3、作函数图象的一般步骤:
(1)取点; (2)描点;(3)连点
两点法——一般取满足函数解析式的较方便的两个点,再连成直线即可。
6、数形结合法求交点:函数的代数表达式与函数图象是紧密联系着的,“数”用“形”表示,由“形”想到“数”,这是我们数学学习中一个很重要的思想方法——数形结合。
一次函数y=kx+b(k≠0)的图象是一条直线
。
所以一次函数y=kx+b的图象也叫做直线y=kx+b。
4、一次函数的图象特征和画法:
5、画函数图象时还应特别注意:需考虑自变量的取值范围。
作业
1.作业本(2):
5.4一次函数的图象(1)
2.方法指导丛书:5.4一次函数的图象(1)
5.4一次函数的图象(1)
情景
在校运会上,A同学和B同学参加了100米赛跑比赛,测得他们的平均速度是
米/秒和8米/秒,根据以下要求:表示他所跑的路程s与所用的时间t的函数关系.
问题1、这个关系能用解析法表示吗?能的话,请表示;
问题2、这个关系能用列表法表示吗?能的话,请表示;
把一个函数的自变量x的值与函数y的对应值分别作为点的横坐标和纵坐标,在直角坐标系中描出它的对应点,所有这些点组成的图形.叫做这个函数的图象。
问题3、(1)函数图象的概念:
(2)思考:根据概念,画一个函数图象需要几个步骤.
(3)
那么,你能用图象法来表示这个关系吗?能的话,画好图象,猜想图象是什么?
(1)取点; (2)描点;(3)连点
解析法
列表法
图象法
问题4、这三种表示法,哪一种比较形象直观、全面?
t
0
3
6
9
12
SA
0
25
50
75
100
解:
SA=
t
(0
≤
t≤
12)
S
B=8t(0
≤t
≤12.5)
t
0
3
6
9
12.5
SB
0
24
48
72
100
A
12.5
B
3
6
12
100
t(秒)
S(米)
0
25
50
1、列表:分别选取若干对自变量与函数的对应值,列成下表.
x
….
-2
-1
0
1
2
….
y=2x
….
….
y=2x+1
….
….
2、描点:在一个平面直角坐标系中,
描出这两组点.用光滑的线连接.
作出一次函数y=2x和Y=2X+1的图象
-4
-2
0
2
4
-3
-1
1
3
5
y
X
O
Y=2X
Y=2X+1
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
1
2
3
4
5
6
7
8
-7
-8
1.请你再找出另外一些满足一次函数y=2x+1的数对出来,看一看以这些数对为坐标的点在不在所画的直线上?
2.在你所画的直线上再取几个点,分别找出各点的横坐标和纵坐标,检验一下这些点的坐标是否满足关系式y=2x+1?
由此可见,一次函数Y=kx+b(k、b为常数,
k≠0
)可以用直角坐标系中的一条直线来表示,
从而这条直线就叫做一次函数Y=kx+b的图象.
所以,一次函数y=kx+b(k≠0)的图象也叫做直线y=kx+b
y
x
0
y=kx+b
2、函数图象的概念包含两个方面的内容:
(1)满足函数解析式的点,一定在这个函数图象上。
(2)反过来,在函数图象上的点的坐标满足函数的解析式。
3.(1)
点(2,9)在函数y=4x+1的图象上吗?
为什么?
(2)
点(-2,5)在函数y=4x+1的图象上吗?
为什么?
感悟:
1.若直线y=2x-3
经过点(1,a),
则a=_____
2.
已知点M(-3,
4)在直线y=
kx+1上,则k的值是__________
解:(1)把x=2代入函数,得y=4×2+1=9,
∴点(2,9)在函数
y=4x+1
的图象上
(2)把x=-2代入函数,得y=4×-2+1=-7≠5,
∴点(-2,5)不在函数y=4x+1的图象上
-1
-1
例1:在同一坐标系作出下列函数
的图象,并求它们与坐标轴的交点坐标.
Y=3x,
y=-3x+2
分析:因为一次函数的图象是一条直线,根据两点确定一条直线,只要画出图象上的两个点,就可以画出一次函数的图象.
对于函数y=3x,
取x=0,得y=0,得到点(0,0);取x=1,得y=3,得到点(1,3)
对于函数y=-3x+2,
取x=0,y=2,得到点(0,2);
取x=1,y=-1,得到点(1,-1)
在坐标系里描出各组点,分别过两点做直线就得到函数图象.
x
y
0
1
2
3
3
1
2
-1
-2
-2
-1
y=3x
y=-3x+2
100
t(秒)
S(米)
0
12.5
S=8t
(0≤t≤12.5)
以(0,0)、(12.5,100)为端点的一条线段.
经过(0,2)、(1,
-1)的一条直线
y=-3x+2
2
x
y
1
1
(1,-1)
.
y=-3x+2
(x<0)
y=-3x+2
(-1
以(-1,5)、(2,-4)为端点的线段,除(-1,5)外.
以(0,2)为端点,经过(-1,5)的射线,除(0,2)外
x
y
0
1
2
3
3
1
2
-1
-2
-2
-1
y=3x
y=-3x+2
(2)对于y=3x
当x=0时,y=0;当y=0时,x=0
∴和x轴、y轴的交点坐标都是(0,0)
当x=0时,y=2;
∴与y轴的交点坐标是(0,2),
当y=0时,x=
,
∴与x轴的交点坐标是(
,0)
(1)对于y=
-3x+2
直接利用函数解析式求
函数图象与坐标轴的交点坐标
求出一次函数与坐标轴的交点坐标
y=
–
3
x+2
y=3x
考考你
1.已知直线y=
-2x+4,它与x轴的交点为A,与y轴的交点为B.
(1).求A,
B两点的坐标.
(2).求?AOB的面积.
(O为坐标原点)
解:(1)取x=0,则y=4;
∴
B(0,4)
取y=0,则-2x+4=0,
解得x=2
∴A(2,0)
A
O
B
(2)∵AO=2
BO=4
∴S△AOB=?×2×4=4
2.一次函数的图象过M(3,2),N(-1,
-
6)
(1)求函数的解析式;
(2)试判断点P(2a,4a-4)是否在函数的图象上,并说明理由;
解:设函数解析式为y=kx+b
梳理一下吧!
2、函数图象的概念包含两个方面的内容:
(1)满足函数解析式的点一定在这个函数的图象上。
(2)在函数图象上的点的坐标一定满足函数解析式。
1、函数图象的概念:
把一个函数的自变量x与对应的函数y的值分别作
为点的横坐标和纵坐标
,
在直角坐标系内描出它的对
应点
,
所有这些点组成的图形叫做该函数的图象.
3、作函数图象的一般步骤:
(1)取点; (2)描点;(3)连点
两点法——一般取满足函数解析式的较方便的两个点,再连成直线即可。
6、数形结合法求交点:函数的代数表达式与函数图象是紧密联系着的,“数”用“形”表示,由“形”想到“数”,这是我们数学学习中一个很重要的思想方法——数形结合。
一次函数y=kx+b(k≠0)的图象是一条直线
。
所以一次函数y=kx+b的图象也叫做直线y=kx+b。
4、一次函数的图象特征和画法:
5、画函数图象时还应特别注意:需考虑自变量的取值范围。
作业
1.作业本(2):
5.4一次函数的图象(1)
2.方法指导丛书:5.4一次函数的图象(1)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
