浙教版九上4.4.1 两个相似三角形 的判定 教案
文档属性
| 名称 | 浙教版九上4.4.1 两个相似三角形 的判定 教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 94.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 00:00:00 | ||
图片预览

文档简介
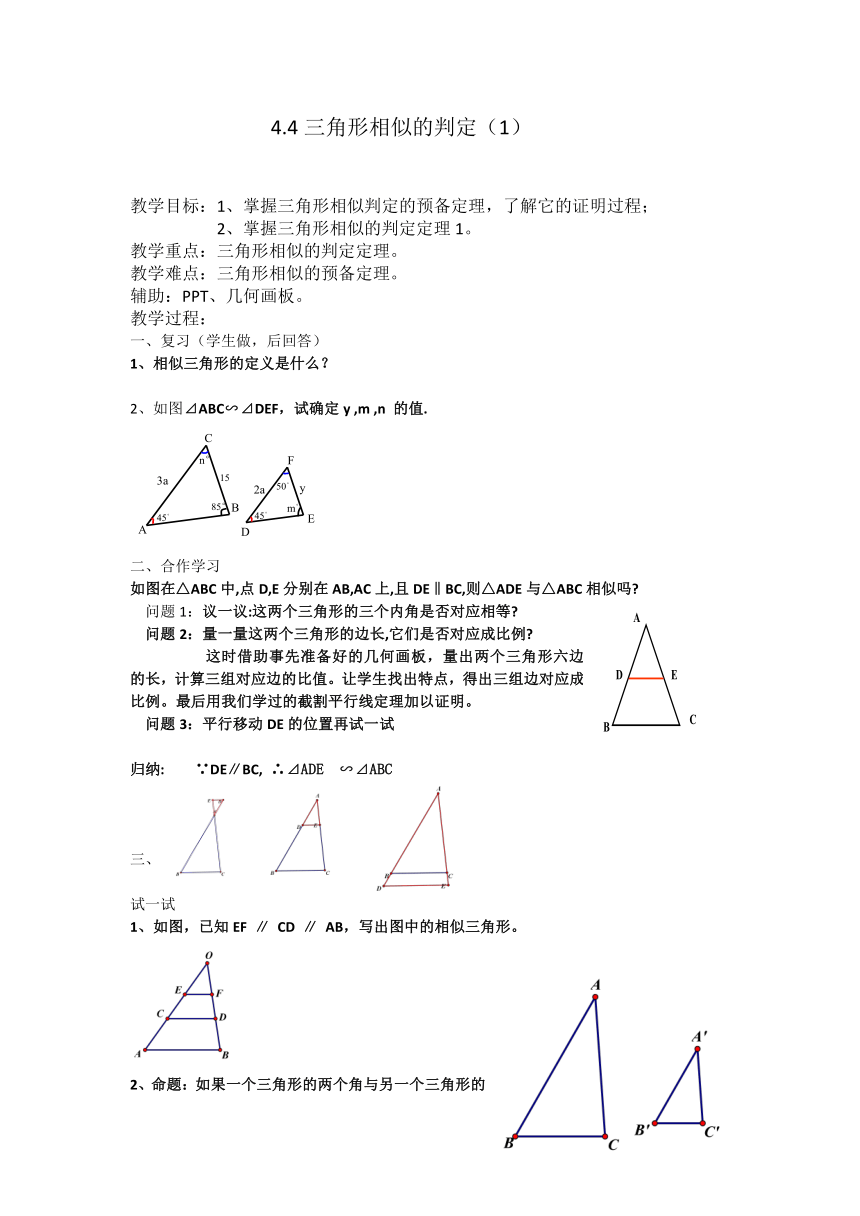
4.4三角形相似的判定(1)
教学目标:1、掌握三角形相似判定的预备定理,了解它的证明过程;
2、掌握三角形相似的判定定理1。
教学重点:三角形相似的判定定理。
教学难点:三角形相似的预备定理。
辅助:PPT、几何画板。
教学过程:
一、复习(学生做,后回答)
1、相似三角形的定义是什么?
2、如图⊿ABC∽⊿DEF,试确定y
,m
,n
的值.
二、合作学习
如图在△ABC中,点D,E分别在AB,AC上,且DE‖BC,则△ADE与△ABC相似吗?
问题1:议一议:这两个三角形的三个内角是否对应相等?
问题2:量一量这两个三角形的边长,它们是否对应成比例?
这时借助事先准备好的几何画板,量出两个三角形六边
的长,计算三组对应边的比值。让学生找出特点,得出三组边对应成比例。最后用我们学过的截割平行线定理加以证明。
问题3:平行移动DE的位置再试一试
归纳:
∵DE∥BC,
∴⊿ADE
∽⊿ABC
三、
试一试
1、如图,已知EF
∥
CD
∥
AB,写出图中的相似三角形。
2、命题:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
问题:1、这是一个命题证明,分几步走?
2、能否构造一个三角形,既与⊿ADE
有关,又与⊿ABC有关,怎么构造?
3、学生思考后,叫举手同学回答(有一定难度),学生讲出一种后,教师再引导,还有没有其余的构造法。
归纳:判定三角形相似的方法:两个角对应相等的两个三角形相似。
问:现在我们有几种方法可以证明两三角形相似?你会选择哪几种?不会选择哪种?
四、练一练
1、已知ΔABC与ΔA/B/C/中,∠B=∠B/=750,∠C=500,∠A/=550,这两个三角形相似吗?为什么?
2、如图,点D、E、F分别在⊿ABC的各边上,且DE∥BC,DF∥AC。找出图中的相似三角形。
3、如图,在⊿
ABC中,
∠
ACB=Rt
∠,CD
⊥
AB于点D,写出图中的相似三角形。
4、已知:如图,在⊙O中,弦AB与弦CD交于点P。
(1)求⊿ADP∽⊿CBP
(2)判断AP·BP=DP·CP是否成立,并给出证明。
五、例题.在一次数学活动课上,为了测量河宽AB,张杰采用了如下方法:从A处沿与AB垂直的直线方向走40m到达C处,插一根标杆,然后沿同方向继续走15m到达D处,再右转90度走到E处,使B,C,E三点恰好在一条直线上,量得DE=20m,这样就可以求出河宽AB.请你算出结果(要求给出解题过程)
问题:你能根据这种图形求出河宽吗?
让学生写出过程,投影展示,一起批改。
你还能有其余的设计方案吗?请画出来。
归纳:生活中的问题如何转化为数学问题,这里构造三角形相似,对应边成比例,求出河宽,形成数学建模。
六、小结:
这节课我们学了哪些知识?用到了什么方法?
教学目标:1、掌握三角形相似判定的预备定理,了解它的证明过程;
2、掌握三角形相似的判定定理1。
教学重点:三角形相似的判定定理。
教学难点:三角形相似的预备定理。
辅助:PPT、几何画板。
教学过程:
一、复习(学生做,后回答)
1、相似三角形的定义是什么?
2、如图⊿ABC∽⊿DEF,试确定y
,m
,n
的值.
二、合作学习
如图在△ABC中,点D,E分别在AB,AC上,且DE‖BC,则△ADE与△ABC相似吗?
问题1:议一议:这两个三角形的三个内角是否对应相等?
问题2:量一量这两个三角形的边长,它们是否对应成比例?
这时借助事先准备好的几何画板,量出两个三角形六边
的长,计算三组对应边的比值。让学生找出特点,得出三组边对应成比例。最后用我们学过的截割平行线定理加以证明。
问题3:平行移动DE的位置再试一试
归纳:
∵DE∥BC,
∴⊿ADE
∽⊿ABC
三、
试一试
1、如图,已知EF
∥
CD
∥
AB,写出图中的相似三角形。
2、命题:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
问题:1、这是一个命题证明,分几步走?
2、能否构造一个三角形,既与⊿ADE
有关,又与⊿ABC有关,怎么构造?
3、学生思考后,叫举手同学回答(有一定难度),学生讲出一种后,教师再引导,还有没有其余的构造法。
归纳:判定三角形相似的方法:两个角对应相等的两个三角形相似。
问:现在我们有几种方法可以证明两三角形相似?你会选择哪几种?不会选择哪种?
四、练一练
1、已知ΔABC与ΔA/B/C/中,∠B=∠B/=750,∠C=500,∠A/=550,这两个三角形相似吗?为什么?
2、如图,点D、E、F分别在⊿ABC的各边上,且DE∥BC,DF∥AC。找出图中的相似三角形。
3、如图,在⊿
ABC中,
∠
ACB=Rt
∠,CD
⊥
AB于点D,写出图中的相似三角形。
4、已知:如图,在⊙O中,弦AB与弦CD交于点P。
(1)求⊿ADP∽⊿CBP
(2)判断AP·BP=DP·CP是否成立,并给出证明。
五、例题.在一次数学活动课上,为了测量河宽AB,张杰采用了如下方法:从A处沿与AB垂直的直线方向走40m到达C处,插一根标杆,然后沿同方向继续走15m到达D处,再右转90度走到E处,使B,C,E三点恰好在一条直线上,量得DE=20m,这样就可以求出河宽AB.请你算出结果(要求给出解题过程)
问题:你能根据这种图形求出河宽吗?
让学生写出过程,投影展示,一起批改。
你还能有其余的设计方案吗?请画出来。
归纳:生活中的问题如何转化为数学问题,这里构造三角形相似,对应边成比例,求出河宽,形成数学建模。
六、小结:
这节课我们学了哪些知识?用到了什么方法?
同课章节目录
