浙教版九上1.2.1 二次函数图像 教案
文档属性
| 名称 | 浙教版九上1.2.1 二次函数图像 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 00:00:00 | ||
图片预览


文档简介
二次函数图像(1)
一、教学目标
1.知识与技能
能够利用描点法画函数的图像。
理解图像中的相关概念(如抛物线、对称轴、顶点、开口方向等)。
体会研究解决数学问题的过程、途径和方法。
2.过程与方法
①.经历二次函数图像的作法。
②.探索二次函数性质,获得利用图像研究函数性质的经验。
③.由函数的图像及性质,对比地学习的图像及性质,并能比较出它们的异同点,培养学生的类比学习能力和发展学生的求同求异思维。
3.情感与态度
①.通过学生自己的探索活动,达到对抛物线自身特点的认识和对二次函数性质的理解。
②.在利用图像讨论二次函数的性质时,让学生尽可能多地合作交流,以便使学生能够从多个角度看问题,进而比较准确地画出二次函数的图像。
二、教学重难点
教学重点:会画函数的图像,并根据图像认识和理解二次函数最基本的性质.
教学难点:用描点法画二次函数的图像。
三、教学过程
(一)欣赏篇(从大桥时代谈起)
师:大家都知道,我们舟山是一个著名的旅游城市,自从进入大桥时代,游客们开始以自驾
游的方式来我们舟山游玩。你们知道他们欣赏的第一道风景线是什么吗?
生:跨海大桥
师:(幻灯片展示跨海大桥)
师:游客们首先要过的是金塘大桥,再是西堠门大桥等。到了岱山,他们还可以看到官山大桥和江南大桥。这些桥不仅壮观,而且也非常漂亮。
师:同学们找找这些桥的共同点?
生:漂亮的弧线
师:我们身边也有这样的曲线。如推铅球时铅球运动轨迹等(多媒体展示)
师:因为这些曲线和抛掷物体的轨迹相似,所以叫做抛物线。其实,抛物线是我们学过的函数二次函数的图像,不信,我们来探究一下。
(二)探究篇1(用描点法画图)
师:二次函数的一般式是什么?
生:
(a≠0)
师:现在我们来探究一下最简单的二次函数和的图像。
师:画函数图像,我们用什么方法?
生:描点法。
师:描点法的步骤怎么样?
生:列表—描点—连线
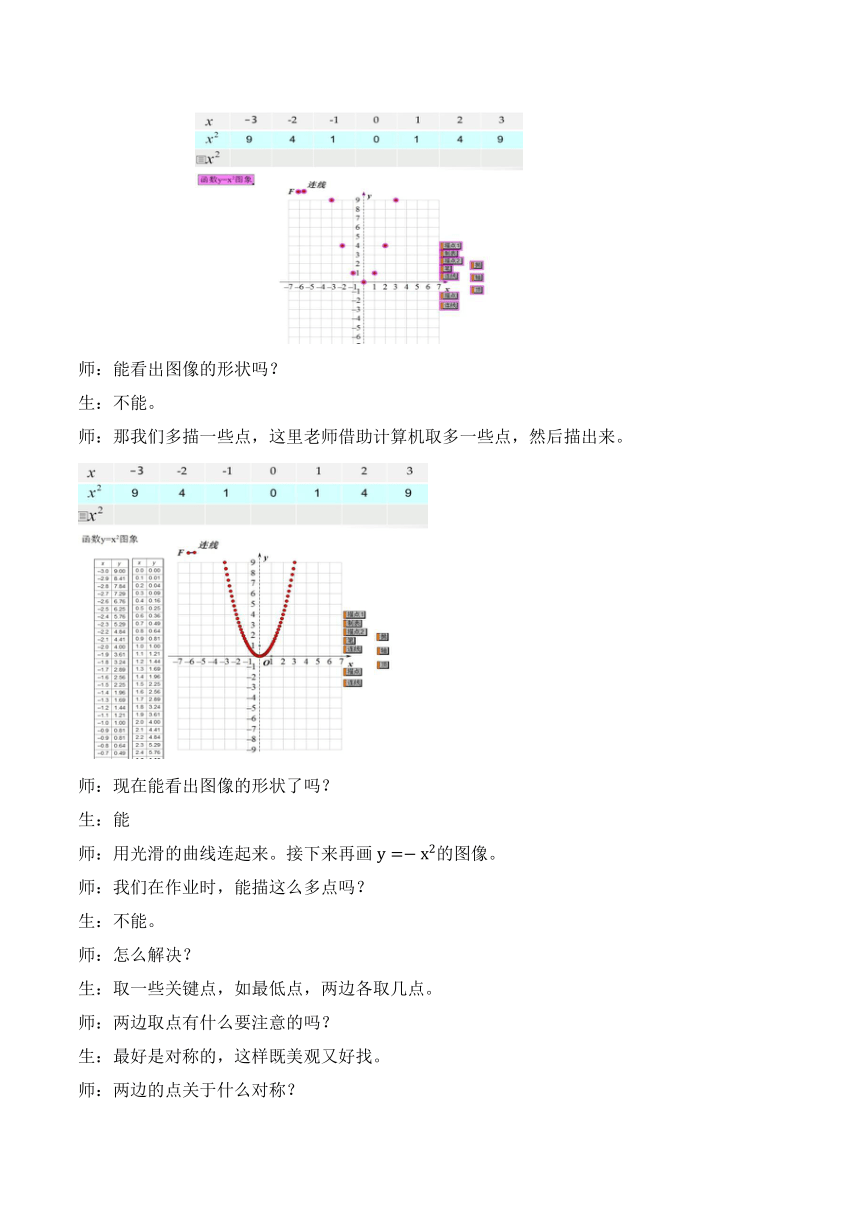
师:我们先来列表
(课件展示,学生填表)
完成后,描点。
师:能看出图像的形状吗?
生:不能。
师:那我们多描一些点,这里老师借助计算机取多一些点,然后描出来。
师:现在能看出图像的形状了吗?
生:能
师:用光滑的曲线连起来。接下来再画的图像。
师:我们在作业时,能描这么多点吗?
生:不能。
师:怎么解决?
生:取一些关键点,如最低点,两边各取几点。
师:两边取点有什么要注意的吗?
生:最好是对称的,这样既美观又好找。
师:两边的点关于什么对称?
生:y轴。
师:最低点的位置有什么特别吗?
生:在对称轴上。
师:(多媒体展示)一般的,画图时在对称轴两边各取3个点,再加上原点就可以了。
师:观察我们画的图像,是不是和抛掷物体的轨迹很像,我们把这样的曲线叫做抛物线。
对称轴是y轴,其中抛物线和对称轴的交点叫顶点。
师:接下来同学们独立完成的图像制作。
生:(动手画函数图像)
师:巡视学生作图,纠正作图过程中出现的问题,比如,连线不是一笔,顶点处不光滑等。
探究篇2(从图像中得性质)
师:结合图像和函数表达式,你发现了什么?你能完成下列表格吗?
生:思考并完成表格。
师:现在我们不仅知道了二次函数的图像是抛物线,还知道了它的相关性质,那么,你能用这些性质解决相关问题吗?
(三)应用篇(用性质解问题)
出示例题
例1、已知二次函数
(a≠0)的图像经过点(-2,-3).
(1)求a的值,并写出这个二次函数的解析式.
(2)说出这个二次函数的顶点坐标、对称轴、开口方向和图像的位置.
师:题中什么是未知的?
生:a
师:怎么求解?
生:把点坐标代入列方程求解。
(学生独立完成)
师:同学们对抛物线的知识掌握的很好,下面老师再来考考大家
练习、已知抛物线y=ax2经过点A(-2,-8)。
(1)求此抛物线的函数解析式;
(2)判断点B(-1,-
4)是否在此抛物线上。
(3)求出此抛物线上纵坐标为-6的点的坐标。
(学生独立完成)
师:如何验证点是否在抛物线上?
生:代入横坐标,看纵坐标是否一致。
师:纵坐标相等,横坐标一定相等吗?
生:不一定,可以有两个。
师:很好,我们来通过图形看看,为什么有两个。
(四)丰收篇(用智慧树总结课堂所得)
师:同学们做题时要注意数形结合。通过这节课的学习,同学们对二次函数的图像一定有所理解。下面同学们和老师一起来完成一幅画。
出示图片
师:这是一棵二次函数图像的智慧树,你觉得树叶上有哪些知识呢?
生:思考填写
师:总结,分享。
马上下课了,这节课很高兴和大家一起探究了二次函数图像,老师祝愿同学们心中的智慧树越长越高,结出更多的果实。
一、教学目标
1.知识与技能
能够利用描点法画函数的图像。
理解图像中的相关概念(如抛物线、对称轴、顶点、开口方向等)。
体会研究解决数学问题的过程、途径和方法。
2.过程与方法
①.经历二次函数图像的作法。
②.探索二次函数性质,获得利用图像研究函数性质的经验。
③.由函数的图像及性质,对比地学习的图像及性质,并能比较出它们的异同点,培养学生的类比学习能力和发展学生的求同求异思维。
3.情感与态度
①.通过学生自己的探索活动,达到对抛物线自身特点的认识和对二次函数性质的理解。
②.在利用图像讨论二次函数的性质时,让学生尽可能多地合作交流,以便使学生能够从多个角度看问题,进而比较准确地画出二次函数的图像。
二、教学重难点
教学重点:会画函数的图像,并根据图像认识和理解二次函数最基本的性质.
教学难点:用描点法画二次函数的图像。
三、教学过程
(一)欣赏篇(从大桥时代谈起)
师:大家都知道,我们舟山是一个著名的旅游城市,自从进入大桥时代,游客们开始以自驾
游的方式来我们舟山游玩。你们知道他们欣赏的第一道风景线是什么吗?
生:跨海大桥
师:(幻灯片展示跨海大桥)
师:游客们首先要过的是金塘大桥,再是西堠门大桥等。到了岱山,他们还可以看到官山大桥和江南大桥。这些桥不仅壮观,而且也非常漂亮。
师:同学们找找这些桥的共同点?
生:漂亮的弧线
师:我们身边也有这样的曲线。如推铅球时铅球运动轨迹等(多媒体展示)
师:因为这些曲线和抛掷物体的轨迹相似,所以叫做抛物线。其实,抛物线是我们学过的函数二次函数的图像,不信,我们来探究一下。
(二)探究篇1(用描点法画图)
师:二次函数的一般式是什么?
生:
(a≠0)
师:现在我们来探究一下最简单的二次函数和的图像。
师:画函数图像,我们用什么方法?
生:描点法。
师:描点法的步骤怎么样?
生:列表—描点—连线
师:我们先来列表
(课件展示,学生填表)
完成后,描点。
师:能看出图像的形状吗?
生:不能。
师:那我们多描一些点,这里老师借助计算机取多一些点,然后描出来。
师:现在能看出图像的形状了吗?
生:能
师:用光滑的曲线连起来。接下来再画的图像。
师:我们在作业时,能描这么多点吗?
生:不能。
师:怎么解决?
生:取一些关键点,如最低点,两边各取几点。
师:两边取点有什么要注意的吗?
生:最好是对称的,这样既美观又好找。
师:两边的点关于什么对称?
生:y轴。
师:最低点的位置有什么特别吗?
生:在对称轴上。
师:(多媒体展示)一般的,画图时在对称轴两边各取3个点,再加上原点就可以了。
师:观察我们画的图像,是不是和抛掷物体的轨迹很像,我们把这样的曲线叫做抛物线。
对称轴是y轴,其中抛物线和对称轴的交点叫顶点。
师:接下来同学们独立完成的图像制作。
生:(动手画函数图像)
师:巡视学生作图,纠正作图过程中出现的问题,比如,连线不是一笔,顶点处不光滑等。
探究篇2(从图像中得性质)
师:结合图像和函数表达式,你发现了什么?你能完成下列表格吗?
生:思考并完成表格。
师:现在我们不仅知道了二次函数的图像是抛物线,还知道了它的相关性质,那么,你能用这些性质解决相关问题吗?
(三)应用篇(用性质解问题)
出示例题
例1、已知二次函数
(a≠0)的图像经过点(-2,-3).
(1)求a的值,并写出这个二次函数的解析式.
(2)说出这个二次函数的顶点坐标、对称轴、开口方向和图像的位置.
师:题中什么是未知的?
生:a
师:怎么求解?
生:把点坐标代入列方程求解。
(学生独立完成)
师:同学们对抛物线的知识掌握的很好,下面老师再来考考大家
练习、已知抛物线y=ax2经过点A(-2,-8)。
(1)求此抛物线的函数解析式;
(2)判断点B(-1,-
4)是否在此抛物线上。
(3)求出此抛物线上纵坐标为-6的点的坐标。
(学生独立完成)
师:如何验证点是否在抛物线上?
生:代入横坐标,看纵坐标是否一致。
师:纵坐标相等,横坐标一定相等吗?
生:不一定,可以有两个。
师:很好,我们来通过图形看看,为什么有两个。
(四)丰收篇(用智慧树总结课堂所得)
师:同学们做题时要注意数形结合。通过这节课的学习,同学们对二次函数的图像一定有所理解。下面同学们和老师一起来完成一幅画。
出示图片
师:这是一棵二次函数图像的智慧树,你觉得树叶上有哪些知识呢?
生:思考填写
师:总结,分享。
马上下课了,这节课很高兴和大家一起探究了二次函数图像,老师祝愿同学们心中的智慧树越长越高,结出更多的果实。
同课章节目录
