浙教版九上2.4 概率的简单应用 教案
文档属性
| 名称 | 浙教版九上2.4 概率的简单应用 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 176.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 00:00:00 | ||
图片预览

文档简介
2.4
简单的概率应用
教学目标:
1、
通过实例进一步丰富对概率的认识。
1、
紧密结合实际,培养应用数学的意识。
教学重难点:
1、
重点:体验概率和实际生活的密切联系。
1、
难点:对例题意的理解。
教学过程:
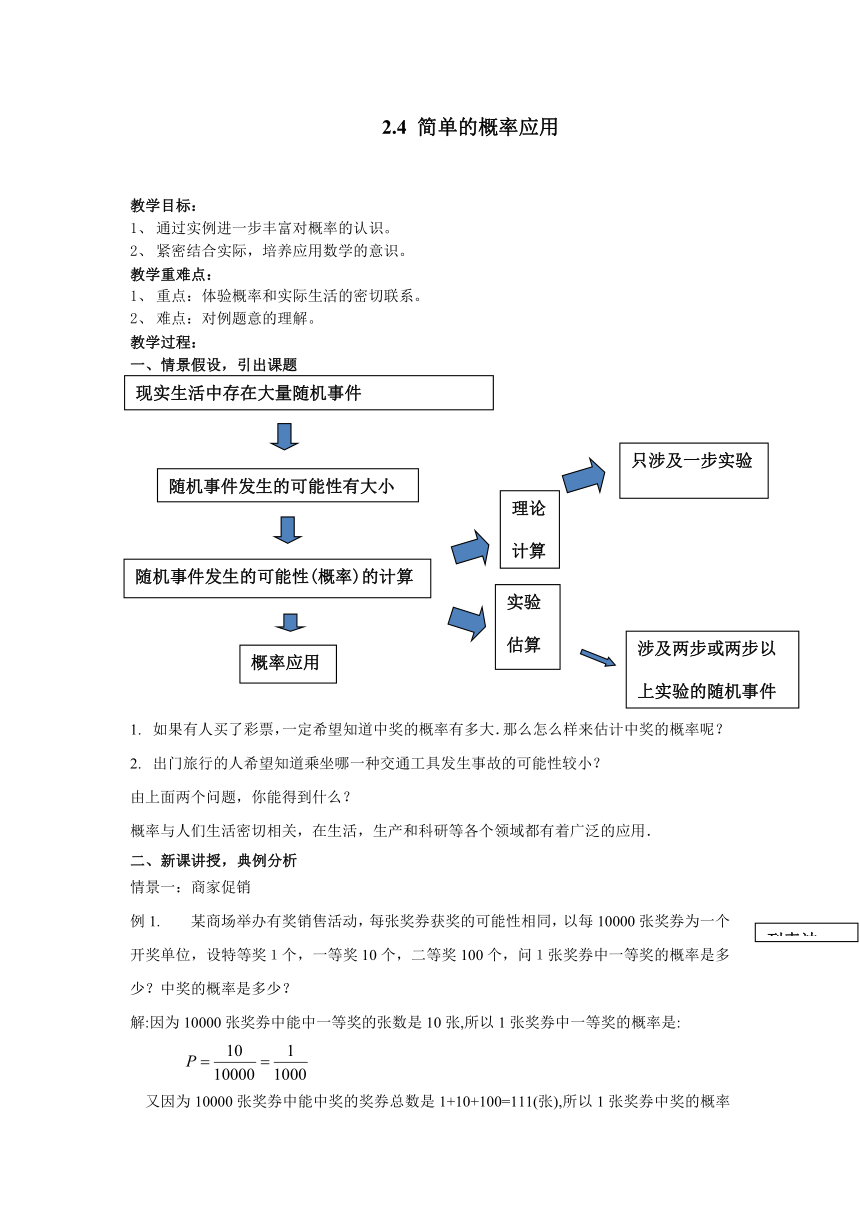
一、情景假设,引出课题
1.
如果有人买了彩票,一定希望知道中奖的概率有多大.那么怎么样来估计中奖的概率呢?
2.
出门旅行的人希望知道乘坐哪一种交通工具发生事故的可能性较小?
由上面两个问题,你能得到什么?
概率与人们生活密切相关,在生活,生产和科研等各个领域都有着广泛的应用.
二、新课讲授,典例分析
情景一:商家促销
例1.
某商场举办有奖销售活动,每张奖券获奖的可能性相同,以每10000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖100个,问1张奖券中一等奖的概率是多少?中奖的概率是多少?
解:因为10000张奖券中能中一等奖的张数是10张,所以1张奖券中一等奖的概率是:
又因为10000张奖券中能中奖的奖券总数是1+10+100=111(张),所以1张奖券中奖的概率是
情景二:社会调查
例2.某班同学在社会实践中,作了关于私家车乘坐人数的统计,他们通过数据的收集与整理,得到在100辆私家车中,统计结果如下表:
每辆私家车乘客数目
1
2
3
4
5
私家车数目
57
28
8
4
3
根据以上结果,估计抽查一辆私家车而它载有超过2名乘客的概率是多少?
情景三:人寿保险
例3.生命表又称死亡表,是人寿保险费率计算的主要依据,如下图是,某年6月中国人民银行发布的中国人寿保险经验生命表,(2012-2013年)的部分摘录,根据表格估算下列概率(结果保留4个有效数字)
年龄x
生存人数lx
死亡人数dx
01
1000000997091
29092010
3031
976611975856
755789
61626364
867685856832845026832209
10853118061281713875
7980
488988456246
3274233348
8182
422898389141
3375733930
(1)某人今年61岁,他当年死亡的概率.
(2)某人今年31岁,他活到62岁的概率.
分析:对lx、dx
的含义举例说明:对于出生的每1000000人,活到30岁的人数l30=976611人(x=30),这一年龄死亡的人数d30=755人,活到31岁的人数l31=976611-755=975856(人).
解:(1)由表知,61岁的生存人数l61=867685,61岁的死亡人数=d6110853,所以所求死亡的概率
(2)由表知,l31=975856,
l62=856832,所以所求的概率:
答:他当年死亡的概率约为0.01251,活到62岁的概率约为0.8780.
(3)一个80岁的人在当年死亡的概率是多少?
(4)如果有10000个80岁的人参加寿险投保,当年死亡的人均赔偿金为a元,那么估计保险公司需支付当年死亡的人的赔偿金额为多少元?
三、应用新知,巩固练习
1、为了用户安全,银行要求存折密码是一个六位数,每个数位上的数都是从0到9的自然数;则不知道密码的人一次猜对密码的概率是多少?
2、一个密码箱的密码,每个数位上的数都是从0到9的自然数;若要使不知道密码的人一次拨对密码的概率小于
,则密码的位数至少需多少位?
四、你说我说,清点收获
本节课你有哪些收获?有何感想?
学会调查、统计,利用学过的概率结合实际问题发表自己的看法,并对事件作出合理的判断和预测,用优化原则作决策,解决实际问题。
五、课堂延伸,作业布置
名校课堂2.4节
现实生活中存在大量随机事件
列表法
树状图
只涉及一步实验
的随机事件发生
的概率
随机事件发生的可能性有大小
理论
计算
随机事件发生的可能性(概率)的计算
实验
估算
涉及两步或两步以
上实验的随机事件
发生的概率
概率应用
P=
简单的概率应用
教学目标:
1、
通过实例进一步丰富对概率的认识。
1、
紧密结合实际,培养应用数学的意识。
教学重难点:
1、
重点:体验概率和实际生活的密切联系。
1、
难点:对例题意的理解。
教学过程:
一、情景假设,引出课题
1.
如果有人买了彩票,一定希望知道中奖的概率有多大.那么怎么样来估计中奖的概率呢?
2.
出门旅行的人希望知道乘坐哪一种交通工具发生事故的可能性较小?
由上面两个问题,你能得到什么?
概率与人们生活密切相关,在生活,生产和科研等各个领域都有着广泛的应用.
二、新课讲授,典例分析
情景一:商家促销
例1.
某商场举办有奖销售活动,每张奖券获奖的可能性相同,以每10000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖100个,问1张奖券中一等奖的概率是多少?中奖的概率是多少?
解:因为10000张奖券中能中一等奖的张数是10张,所以1张奖券中一等奖的概率是:
又因为10000张奖券中能中奖的奖券总数是1+10+100=111(张),所以1张奖券中奖的概率是
情景二:社会调查
例2.某班同学在社会实践中,作了关于私家车乘坐人数的统计,他们通过数据的收集与整理,得到在100辆私家车中,统计结果如下表:
每辆私家车乘客数目
1
2
3
4
5
私家车数目
57
28
8
4
3
根据以上结果,估计抽查一辆私家车而它载有超过2名乘客的概率是多少?
情景三:人寿保险
例3.生命表又称死亡表,是人寿保险费率计算的主要依据,如下图是,某年6月中国人民银行发布的中国人寿保险经验生命表,(2012-2013年)的部分摘录,根据表格估算下列概率(结果保留4个有效数字)
年龄x
生存人数lx
死亡人数dx
01
1000000997091
29092010
3031
976611975856
755789
61626364
867685856832845026832209
10853118061281713875
7980
488988456246
3274233348
8182
422898389141
3375733930
(1)某人今年61岁,他当年死亡的概率.
(2)某人今年31岁,他活到62岁的概率.
分析:对lx、dx
的含义举例说明:对于出生的每1000000人,活到30岁的人数l30=976611人(x=30),这一年龄死亡的人数d30=755人,活到31岁的人数l31=976611-755=975856(人).
解:(1)由表知,61岁的生存人数l61=867685,61岁的死亡人数=d6110853,所以所求死亡的概率
(2)由表知,l31=975856,
l62=856832,所以所求的概率:
答:他当年死亡的概率约为0.01251,活到62岁的概率约为0.8780.
(3)一个80岁的人在当年死亡的概率是多少?
(4)如果有10000个80岁的人参加寿险投保,当年死亡的人均赔偿金为a元,那么估计保险公司需支付当年死亡的人的赔偿金额为多少元?
三、应用新知,巩固练习
1、为了用户安全,银行要求存折密码是一个六位数,每个数位上的数都是从0到9的自然数;则不知道密码的人一次猜对密码的概率是多少?
2、一个密码箱的密码,每个数位上的数都是从0到9的自然数;若要使不知道密码的人一次拨对密码的概率小于
,则密码的位数至少需多少位?
四、你说我说,清点收获
本节课你有哪些收获?有何感想?
学会调查、统计,利用学过的概率结合实际问题发表自己的看法,并对事件作出合理的判断和预测,用优化原则作决策,解决实际问题。
五、课堂延伸,作业布置
名校课堂2.4节
现实生活中存在大量随机事件
列表法
树状图
只涉及一步实验
的随机事件发生
的概率
随机事件发生的可能性有大小
理论
计算
随机事件发生的可能性(概率)的计算
实验
估算
涉及两步或两步以
上实验的随机事件
发生的概率
概率应用
P=
同课章节目录
