浙教版九上3.5.1 圆周角 教案

3.5圆周角(1)
教学目标:
1.
理解圆周角的概念.
2.
经历探索圆周角定理的过程.
3.
掌握圆周角定理和它的推论.
4.
会运用圆周角定理及其推论解决简单的几何问题.
教学重点:圆周角定理
教学难点:圆周角定理的证明要分三种情况讨论,有一定的难度是本节的教学难点.
教法:探索式,启发式,合作学习,直观法学法:动手实验,合作学习
教学过程:
复习旧知,创设情景:
1、请说出圆心角的定义
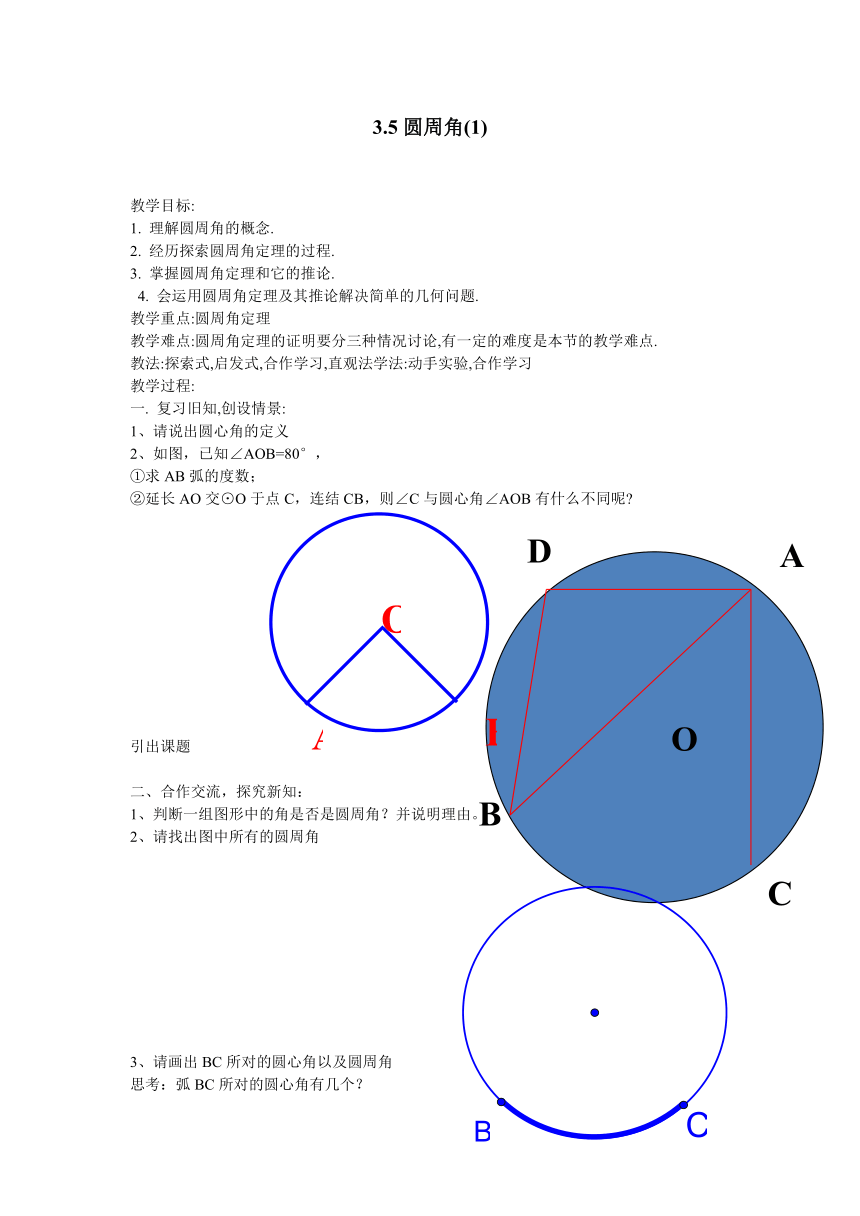
2、如图，已知∠AOB=80°，
①求AB弧的度数；
②延长AO交⊙O于点C，连结CB，则∠C与圆心角∠AOB有什么不同呢?
引出课题
二、合作交流，探究新知：
1、判断一组图形中的角是否是圆周角？并说明理由。
2、请找出图中所有的圆周角
请画出BC所对的圆心角以及圆周角
思考：弧BC所对的圆心角有几个？
弧BC所对的圆周角有几个？
一个圆的圆心与圆周角在位置上有几种关系？
探索研究：如果圆周角和圆心角对着同一条弧，那么这两个角存在怎样的关系？请告诉大家你的数学猜想。
得出圆周角定理：圆周角的度数等于它所对的弧上圆心角的一半。
例题解析，应用巩固：
问题1、如图1,在⊙O中,∠C,∠D,∠E的大小有什么关系?为什么?
总结：同弧所对的圆周角相等
问题2、如图2，BC是⊙O的直径，A是⊙O上任一点，你能确定∠BAC的度数吗?
问题3：如图3，圆周角∠BAC=90?，弦BC经过圆心O吗？为什么？
总结：圆周角定理的推论：
半圆（或直径）所对的圆周角是直角；
90°的圆周角所对的弦是直径。
练习：
1、如图，已知在⊙
O
中，∠BOC
=150°，求∠A
2、已知一条弧所对的圆周角等于500，则这条弧所对的圆心角是多少度？
3、已知一条弧的度数为400，求这条弧所对的圆心角和圆周角的度数。
4、一条弧所对的圆心角的度数为960，求这条弧的度数和它所对的圆周角的度数。
课堂总结：这节课我们都有什么收获？
圆周角的定义：顶点在圆上，两边都与圆相交的角。
圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半。
圆周角定理的推论：半圆（或直径）所对的圆周角是直角；
900的圆周角所对的弦是直径。
布置作业：
作业本（2）上3.5圆周角(1)
A
B
C
D
O
O
A
B
O
C
B
图1
●O
C
A
B
D
E
图1
●O
C
A
B
D
E
B
A
O
C
图2
●O
B
C
A
图3
A
B
C
O