1.4二次函数的应用习题精练 2021-2022学年浙教版数学九年级上册(Word版 含答案)
文档属性
| 名称 | 1.4二次函数的应用习题精练 2021-2022学年浙教版数学九年级上册(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 129.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-25 00:00:00 | ||
图片预览



文档简介
浙教版九年级第1章1.4二次函数的应用习题精练
一、选择题
向上抛出的小球离地面的高度是其运动时间的二次函数,小甬相隔2秒依次抛出两个小球,假设两个小球出手时离地面高度相同,在各自抛出后秒时达到相同的离地面最大高度若第一个小球抛出后t秒时在空中与第二个小球离地面高度相同,则?
?
A.
B.
C.
D.
某商场降价销售一批名牌衬衫,已知所获利利元与降价金额元之间满足函数关系式,则获利最多为
A.
15元
B.
400元
C.
800元
D.
1250元
如图,池中心竖直水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管的长为
A.
B.
C.
D.
如图,在平面直角坐标系中,直线与抛物线交于,两点,则关于x的不等式的解集是?
?
A.
B.
C.
D.
或
在同一坐标系下,抛物线和直线的图象如图所示,那么不等式的解集是
A.
B.
C.
D.
?
或
如图,二次函数的图象与x轴交于和两点,当函数值时,自变量x的取值范围是?
???
A.
B.
C.
D.
小颖用计算器探索方程的根,作出如图所示的图象,并求得一个近似根,则方程的另一个近似根结果精确到为?
???
A.
B.
C.
D.
已知二次函数中,y与x的部分对应值如下表,则方程的一个解的范围是?
??
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
x
y
A.
B.
C.
D.
用一根长60cm的铁丝围成一个矩形,那么矩形的面积与它的一边长之间的函数关系式为
A.
B.
C.
D.
某农机厂四月份生产零件60万个,设该厂第二季度平均每月的增长率为x,如果第二季度共生产零件y万个,那么y与x满足的函数关系式是?
?
A.
B.
C.
D.
二、填空题
加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”在特定条件下,可食用率y与加工时间单位:满足函数表达式,则最佳加工时间为______min.
如图,是二次函数的部分图象,则不等式的解集是______.
若二次函数的部分图像如图所示,则方程的根为________.
中国的新冠疫苗受到世界各国的高度认可,中国人民完全免费接种,但对国外要收取费用已知出口某国的疫苗原价是400元剂,每周可出口400000剂,在该国恳请对其优惠销售的条件下,每剂的售价每降低10元,每周可多出口100000剂,设出口疫苗的销售收入为y元,销售价格为x元剂,则y与x之间的函数表达式为??????????.
三、解答题
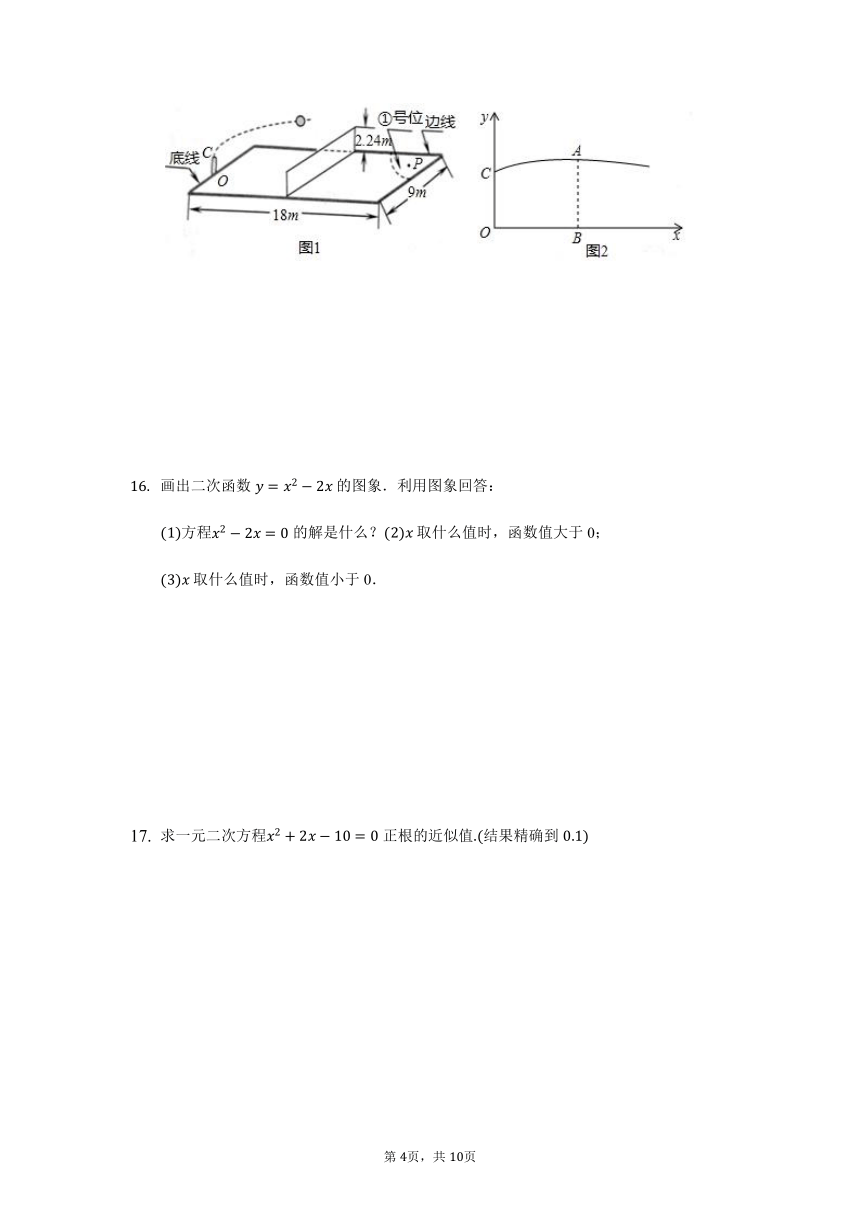
如图1,排球场长为18m,宽为9m,网高为队员站在底线O点处发球,球从点O的正上方的C点发出,运动路线是抛物线的一部分,当球运动到最高点A时,高度为即这时水平距离,以直线OB为x轴,直线OC为y轴,建立平面直角坐标系,如图2.
若球向正前方运动即x轴垂直于底线,求球运动的高度与水平距离之间的函数关系式不必写出x取值范围并判断这次发球能否过网?是否出界?说明理由;
若球过网后的落点是对方场地号位内的点如图1,点P距底线1m,边线,问发球点O在底线上的哪个位置?参考数据:取
画出二次函数的图象.利用图象回答:
方程的解是什么?取什么值时,函数值大于0;
取什么值时,函数值小于0.
求一元二次方程正根的近似值结果精确到
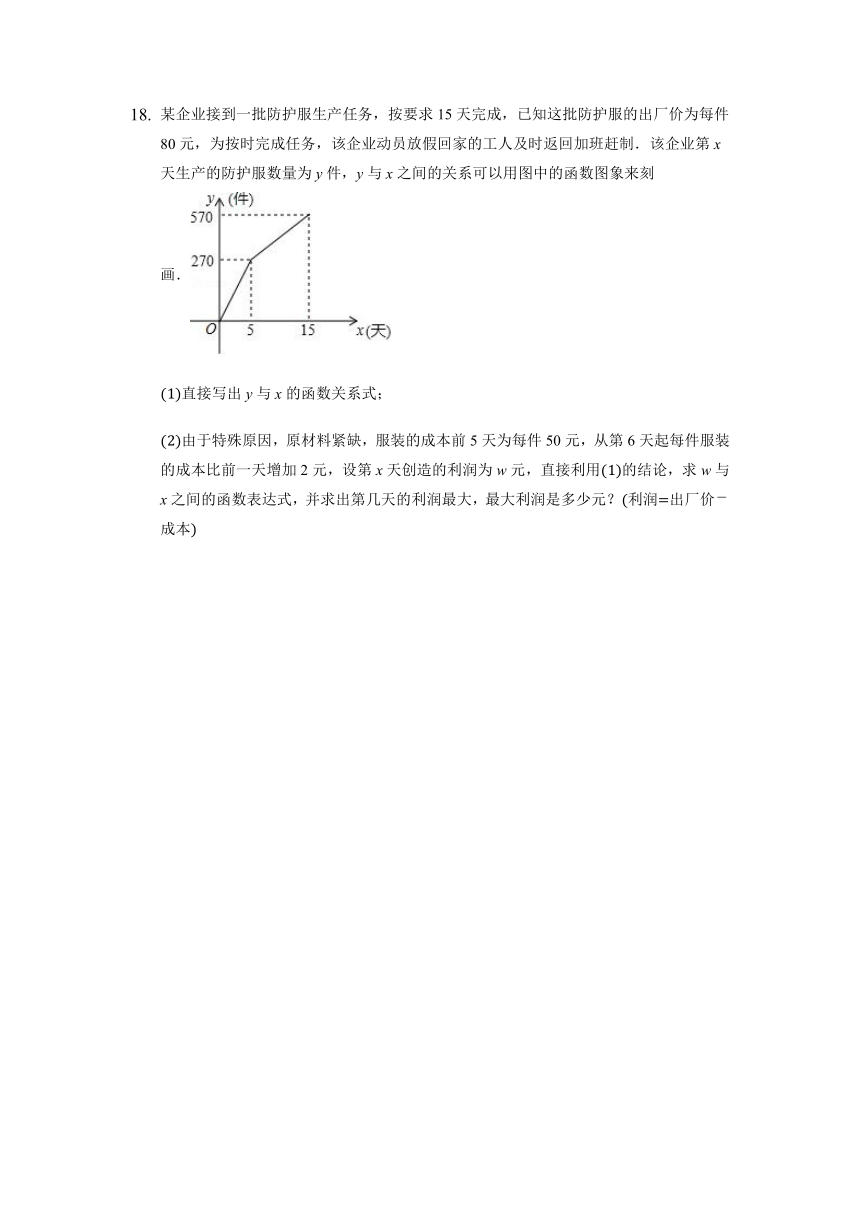
某企业接到一批防护服生产任务,按要求15天完成,已知这批防护服的出厂价为每件80元,为按时完成任务,该企业动员放假回家的工人及时返回加班赶制.该企业第x天生产的防护服数量为y件,y与x之间的关系可以用图中的函数图象来刻画.
直接写出y与x的函数关系式;
由于特殊原因,原材料紧缺,服装的成本前5天为每件50元,从第6天起每件服装的成本比前一天增加2元,设第x天创造的利润为w元,直接利用的结论,求w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?利润出厂价成本
答案和解析
1.【答案】A【解析】解:设抛出x秒时,小球离地面的高度为y,
各自抛出后秒时到达相同的最大离地高度为h,
结合已知可得,为不等于0的常数,
由题意得,
解得.
2.【答案】D
【解析】解:对于抛物线,
,
时,y有最大值,最大值为1250,
故选:D.
3.【答案】D
【解析】解:由于在距池中心的水平距离为1m时达到最高,高度为3m,
则设抛物线的解析式为:
,
代入求得:.
将a值代入得到抛物线的解析式为:
,
令,则.
则水管长为,
故选:D.??
4.【答案】D
【解析】解:观察题图可知,当或时,直线在抛物线的上方,
不等式的解集为或.
故选D.
5.【答案】B
【解析】解:由图可知,抛物线和直线的交点坐标为,,
所以,不等式的解集是.
故选B.??
6.【答案】C
【解析】?解:二次函数的图象与x轴交于和两点,函数开口向下,
函数值时,自变量x的取值范围是,
故选C.??
7.【答案】A
【解析】解:抛物线与x轴的一个交点近似为,又抛物线的对称轴为:,
另一个交点坐标近似为:,
则方程的另一个近似根为,
故选A.??
8.【答案】C
【解析】
解:由表格中的数据看出和更接近于0,
故x应取对应的范围为:,
故选C.??
9.【答案】C
【解析】
解:由题意得:矩形的另一边长,
矩形的面积与它的一边长之间的函数关系式为.
故选C.??
10.【答案】B
【解析】略
11.【答案】
【解析】解:根据题意:,
当时,y取得最大值,
则最佳加工时间为.
故答案为:.
12.【答案】
【解析】解:对称轴,抛物线与x轴的交点,
另一个与x轴交点的坐标,
二次函数的图象与x轴交点坐标为、,
而,
即,
.
故答案为:.
13.【答案】,
【解析】
解:二次函数的对称轴为,
由图像可得二次函数与x轴的一个交点为,
二次函数的对称轴为,
它与x轴的另一个交点为,
将变形为,
的解为,,
的解为,.
故答案为,.??
14.【答案】?
【解析】销售收入每剂销售价格销售剂数,
.
15【答案】解:设抛物线的表达式为:,
将,代入上式并解得:,
故抛物线的表达式为:;
当时,,
当时,,
故这次发球过网,但是出界了;
如图,分别作底线、边线的平行线PQ、OQ交于点Q,
在中,,
当时,,解得:或舍去,
,而,
故,
,
发球点O在底线上且距右边线米处.
16.【答案】略
【解析】略
17.【答案】解:方程根是函数与x轴交点的横坐标.
作出二次函数的图象,如图所示,
由图象可知方程的正根在2和3之间.
当时,;当时,;
因此,是方程正根的近似值,
故一元二次方程正根的近似值为.
18.【答案】解:;
根据题意得
,
答:第8天时利润最大,最大利润是8640元.
第2页,共2页
一、选择题
向上抛出的小球离地面的高度是其运动时间的二次函数,小甬相隔2秒依次抛出两个小球,假设两个小球出手时离地面高度相同,在各自抛出后秒时达到相同的离地面最大高度若第一个小球抛出后t秒时在空中与第二个小球离地面高度相同,则?
?
A.
B.
C.
D.
某商场降价销售一批名牌衬衫,已知所获利利元与降价金额元之间满足函数关系式,则获利最多为
A.
15元
B.
400元
C.
800元
D.
1250元
如图,池中心竖直水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管的长为
A.
B.
C.
D.
如图,在平面直角坐标系中,直线与抛物线交于,两点,则关于x的不等式的解集是?
?
A.
B.
C.
D.
或
在同一坐标系下,抛物线和直线的图象如图所示,那么不等式的解集是
A.
B.
C.
D.
?
或
如图,二次函数的图象与x轴交于和两点,当函数值时,自变量x的取值范围是?
???
A.
B.
C.
D.
小颖用计算器探索方程的根,作出如图所示的图象,并求得一个近似根,则方程的另一个近似根结果精确到为?
???
A.
B.
C.
D.
已知二次函数中,y与x的部分对应值如下表,则方程的一个解的范围是?
??
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
x
y
A.
B.
C.
D.
用一根长60cm的铁丝围成一个矩形,那么矩形的面积与它的一边长之间的函数关系式为
A.
B.
C.
D.
某农机厂四月份生产零件60万个,设该厂第二季度平均每月的增长率为x,如果第二季度共生产零件y万个,那么y与x满足的函数关系式是?
?
A.
B.
C.
D.
二、填空题
加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”在特定条件下,可食用率y与加工时间单位:满足函数表达式,则最佳加工时间为______min.
如图,是二次函数的部分图象,则不等式的解集是______.
若二次函数的部分图像如图所示,则方程的根为________.
中国的新冠疫苗受到世界各国的高度认可,中国人民完全免费接种,但对国外要收取费用已知出口某国的疫苗原价是400元剂,每周可出口400000剂,在该国恳请对其优惠销售的条件下,每剂的售价每降低10元,每周可多出口100000剂,设出口疫苗的销售收入为y元,销售价格为x元剂,则y与x之间的函数表达式为??????????.
三、解答题
如图1,排球场长为18m,宽为9m,网高为队员站在底线O点处发球,球从点O的正上方的C点发出,运动路线是抛物线的一部分,当球运动到最高点A时,高度为即这时水平距离,以直线OB为x轴,直线OC为y轴,建立平面直角坐标系,如图2.
若球向正前方运动即x轴垂直于底线,求球运动的高度与水平距离之间的函数关系式不必写出x取值范围并判断这次发球能否过网?是否出界?说明理由;
若球过网后的落点是对方场地号位内的点如图1,点P距底线1m,边线,问发球点O在底线上的哪个位置?参考数据:取
画出二次函数的图象.利用图象回答:
方程的解是什么?取什么值时,函数值大于0;
取什么值时,函数值小于0.
求一元二次方程正根的近似值结果精确到
某企业接到一批防护服生产任务,按要求15天完成,已知这批防护服的出厂价为每件80元,为按时完成任务,该企业动员放假回家的工人及时返回加班赶制.该企业第x天生产的防护服数量为y件,y与x之间的关系可以用图中的函数图象来刻画.
直接写出y与x的函数关系式;
由于特殊原因,原材料紧缺,服装的成本前5天为每件50元,从第6天起每件服装的成本比前一天增加2元,设第x天创造的利润为w元,直接利用的结论,求w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?利润出厂价成本
答案和解析
1.【答案】A【解析】解:设抛出x秒时,小球离地面的高度为y,
各自抛出后秒时到达相同的最大离地高度为h,
结合已知可得,为不等于0的常数,
由题意得,
解得.
2.【答案】D
【解析】解:对于抛物线,
,
时,y有最大值,最大值为1250,
故选:D.
3.【答案】D
【解析】解:由于在距池中心的水平距离为1m时达到最高,高度为3m,
则设抛物线的解析式为:
,
代入求得:.
将a值代入得到抛物线的解析式为:
,
令,则.
则水管长为,
故选:D.??
4.【答案】D
【解析】解:观察题图可知,当或时,直线在抛物线的上方,
不等式的解集为或.
故选D.
5.【答案】B
【解析】解:由图可知,抛物线和直线的交点坐标为,,
所以,不等式的解集是.
故选B.??
6.【答案】C
【解析】?解:二次函数的图象与x轴交于和两点,函数开口向下,
函数值时,自变量x的取值范围是,
故选C.??
7.【答案】A
【解析】解:抛物线与x轴的一个交点近似为,又抛物线的对称轴为:,
另一个交点坐标近似为:,
则方程的另一个近似根为,
故选A.??
8.【答案】C
【解析】
解:由表格中的数据看出和更接近于0,
故x应取对应的范围为:,
故选C.??
9.【答案】C
【解析】
解:由题意得:矩形的另一边长,
矩形的面积与它的一边长之间的函数关系式为.
故选C.??
10.【答案】B
【解析】略
11.【答案】
【解析】解:根据题意:,
当时,y取得最大值,
则最佳加工时间为.
故答案为:.
12.【答案】
【解析】解:对称轴,抛物线与x轴的交点,
另一个与x轴交点的坐标,
二次函数的图象与x轴交点坐标为、,
而,
即,
.
故答案为:.
13.【答案】,
【解析】
解:二次函数的对称轴为,
由图像可得二次函数与x轴的一个交点为,
二次函数的对称轴为,
它与x轴的另一个交点为,
将变形为,
的解为,,
的解为,.
故答案为,.??
14.【答案】?
【解析】销售收入每剂销售价格销售剂数,
.
15【答案】解:设抛物线的表达式为:,
将,代入上式并解得:,
故抛物线的表达式为:;
当时,,
当时,,
故这次发球过网,但是出界了;
如图,分别作底线、边线的平行线PQ、OQ交于点Q,
在中,,
当时,,解得:或舍去,
,而,
故,
,
发球点O在底线上且距右边线米处.
16.【答案】略
【解析】略
17.【答案】解:方程根是函数与x轴交点的横坐标.
作出二次函数的图象,如图所示,
由图象可知方程的正根在2和3之间.
当时,;当时,;
因此,是方程正根的近似值,
故一元二次方程正根的近似值为.
18.【答案】解:;
根据题意得
,
答:第8天时利润最大,最大利润是8640元.
第2页,共2页
同课章节目录
