浙教版七上3.4 实数的其运算 教案

姓名
年级
性别
学校
总课时____第___课
教学目标
知识点：实数的分类及运算考点：无理数、实数分类、实数的运算方法：一对一面授
难点重点
重点：平方根、立方根的运算难点：实数的分类、实数的混合运算
课堂教学过程
课前检查
作业完成情况：优□
良□
中□
差□
建议__________________________________________
过程
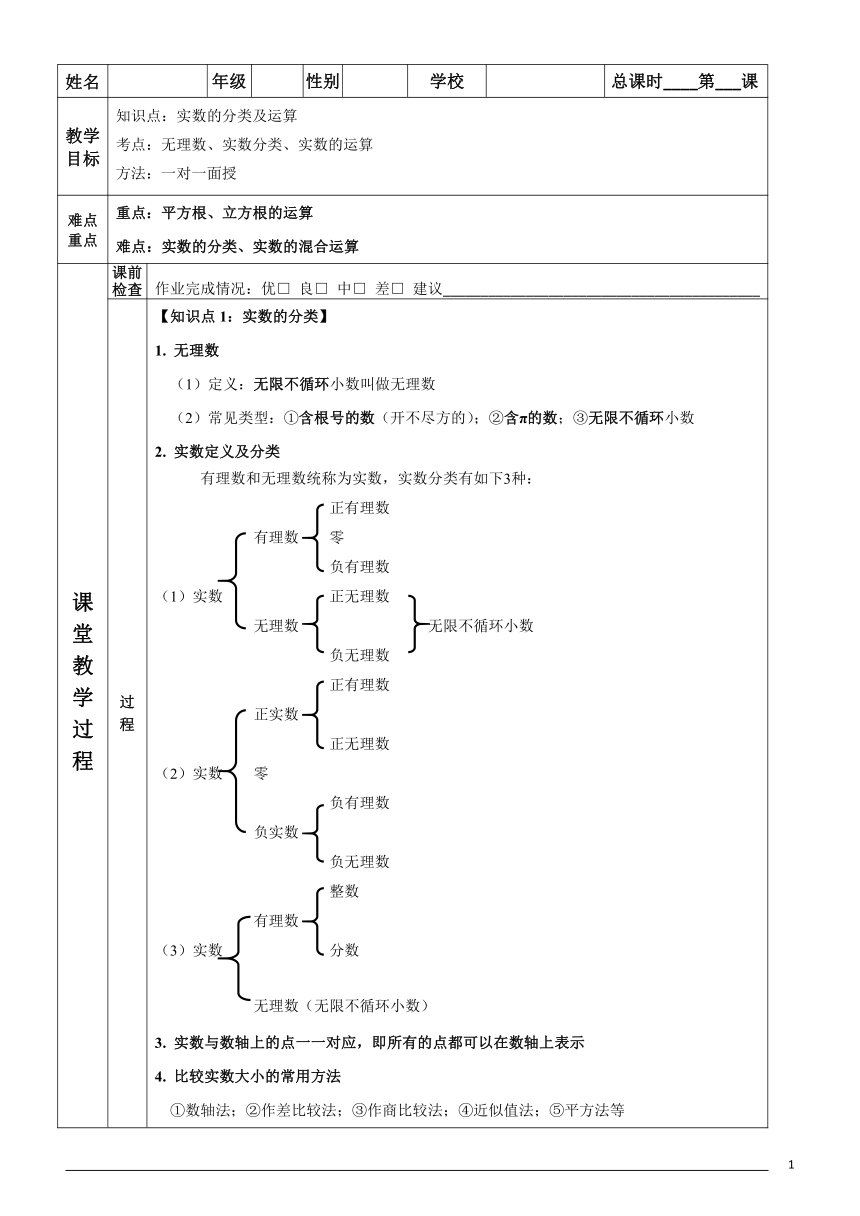
【知识点1：实数的分类】
1.
无理数
（1）定义：无限不循环小数叫做无理数
（2）常见类型：①含根号的数（开不尽方的）；②含π的数；③无限不循环小数2.
实数定义及分类有理数和无理数统称为实数，实数分类有如下3种：正有理数有理数
零负有理数（1）实数
正无理数无理数
无限不循环小数负无理数正有理数正实数
正无理数（2）实数
零
负有理数负实数
负无理数整数有理数
（3）实数
分数无理数（无限不循环小数）
3.
实数与数轴上的点一一对应，即所有的点都可以在数轴上表示4.
比较实数大小的常用方法
①数轴法；②作差比较法；③作商比较法；④近似值法；⑤平方法等【例题讲解】【例1】判断下面的语句对不对？并说明判断的理由.①无限小数都是无理数；
②无理数都是无限小数；③带根号的数都是无理数；
④有理数都是实数，实数不都是有理数；⑤实数都是无理数，无理数都是实数；
⑥实数的绝对值都是非负实数；⑦有理数都可以表示成分数的形式.【例2】填空.（1）相反数等于它本身的数是　　　　；
（2）倒数等于它本身的数是　　　　；（3）平方等于它本身的数是　　　　；
（4）平方根等于它本身的数是　　　　；（5）算术平方根等于它本身的数是　　　　；（6）立方等于它本身的数是　　　　；（7）立方根等于它本身的数是　　　　；
（8）绝对值等于它本身的数是　　　　．[来源:Zxx【例3】下列各数中，不是无理数的是（　
　）A.
　　B.
0.5　　C.
2　　　D.
0.151151115…【例4】下列说法中，正确的是（　　　）A.都是无理数　　　　　　B.
无理数包括正无理数、负无理数和零C.
实数分为正实数和负实数两类　　　D.
绝对值最小的实数是0【例5】把下列各数填入相应的集合内：－11，，3，，0，，，－π，0.4，.有理数集合：{
}；无理数集合：{
}；正实数集合：{
}；实数集合：
{
}．【例6】若有理数满足，求的值.【巩固练习】1.
下列说法正确的是（
）A．不存在最小的实数
B．正数、负数统称有理数C．两个无理数的和一定是无理数
D．两个无理数的积一定是无理数2.
如图，已知正方形的边长为1，则阴影部分的面积与下列各数最接近的是（
）A．0.1
B．0.2
C．0.3
D．0.4
第2题
第3题3.实数
，
在数轴上的位置如图所示，则化简
的结果为
?．4.
在实数范围内，下列判断正确的是（
）A．若，则
B．若，则
C．若，则
D．若，则5.
有三个数，，，将他们从大到小排列为______________.6.
已知0＜＜1，则在①；②；③；④，从大到小排列为______________.7.
如图，一只蚂蚁从点A沿数轴向右爬行2个单位长度到达点B，已知点A表示－，设点B所表示的数为m.(1)求m的值．(2)求|m－1|＋|m＋2|的值．8.
若与互为相反数，与互为倒数，的倒数等于它本身，试化简：
【知识要点2：实数的运算】实数混合运算的顺序：先算________和_________，再算________，最后算_________，如果遇到括号，应先算__________.【例题讲解】【例7】下列运算中，正确的有（
）①－＝－；
②＝±4；③＝＋＝；
④＝－＝－3.A．1个
B．2个
C．3个
D．4个【例8】将，，这三个数按从小到大的顺序用“<”号连接起来：______________.【例9】计算：（1）＋－()0
（2）2÷＋－(－1)2015＋|－2|
（3）(－1)2＋|2－|－＋
（4）++|﹣2|（5）
（6）【例10】已知是一个正整数，求满足条件的最小正整数x的值．【例11】已知，求的值.【拓展型专题】1.
阅读下面问题：
；
.
试求：（1）的值；（2）（为正整数）的值.（3）的值.2.
小明是一位善于思考，勇于创新的同学．在学习了有关平方根的知识后，小明知道负数没有平方根；比如：因为没有一个数的平方等于－1，所以－1没有平方根．有一天，小明想：如果存在一个数i，使i2＝－1，那么(－i)2＝－1，因此－1就有两个平方根了．进一步，小明想：因为(±2i)2＝－4，所以－4的平方根就是±2i；因为(±3i)2＝－9，所以－9的平方根就是±3i.请你根据上面的信息解答下列问题：（1）求－16，－25的平方根.
（2）求i3，i4，i5，i6，i7，i8，…的值，你发现了什么规律？将你发现的规律用式子表示出来．3.
观察并计算下列各式：（1）＝_______；
（2）＝_______;（3）＝________；
（4）＝_________；（5）猜想的值．【巩固训练】1.
求下列代数式的值.（1）若为实数，且，求的值.（2）已知为实数，且互为倒数，互为相反数，的绝对值是，求代数式的值.2.（1）“＜”、“＞”或“＝”填空：
（2）由以上可知：
；
；
（3）计算（结构保留根号）：
???
2
5