1.4二次函数的应用 选择题专题训练(Word版 附答案)2021-2022学年浙教版九年级数学上册
文档属性
| 名称 | 1.4二次函数的应用 选择题专题训练(Word版 附答案)2021-2022学年浙教版九年级数学上册 |
|
|
| 格式 | doc | ||
| 文件大小 | 225.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 00:00:00 | ||
图片预览




文档简介
2021-2022学年浙教版九年级数学上册《1.4二次函数的应用》选择题专题训练(附答案)
1.抛物线C1:y1=mx2﹣4mx+2n﹣1与平行于x轴的直线交于A、B两点,且A点坐标为(﹣1,2),请结合图象分析以下结论:①对称轴为直线x=2;②抛物线与y轴交点坐标为(0,﹣1);③m>;④若抛物线C2:y2=ax2(a≠0)与线段AB恰有一个公共点,则a的取值范围是≤a<2;⑤不等式mx2﹣4mx+2n>0的解作为函数C1的自变量的取值时,对应的函数值均为正数,其中正确结论的个数有( )
A.2个
B.3个
C.4个
D.5个
2.已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1.则下列说法中正确的是( )
A.点火后9s和点火后13s的升空高度相同
B.点火后24s火箭落于地面
C.点火后10s的升空高度为139m
D.火箭升空的最大高度为145m
3.如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和
其中正确结论的个数是( )
A.1
B.2
C.3
D.4
4.已知抛物线y=ax2+bx+c(a,b,c为常数,a≠0)经过点(﹣1,0),(0,3),其对称轴在y轴右侧.有下列结论:
①抛物线经过点(1,0);②方程ax2+bx+c=2有两个不相等的实数根;
③﹣3<a+b<3其中,正确结论的个数为( )
A.0
B.1
C.2
D.3
5.函数y=ax2+2ax+m(a<0)的图象过点(2,0),则使函数值y<0成立的x的取值范围是( )
A.x<﹣4或x>2
B.﹣4<x<2
C.x<0或x>2
D.0<x<2
6.如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:
①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.其中正确的有( )
A.4个
B.3个
C.2个
D.1个
7.一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮筐内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是( )
A.此抛物线的解析式是y=﹣x2+3.5
B.篮圈中心的坐标是(4,3.05)
C.此抛物线的顶点坐标是(3.5,0)
D.篮球出手时离地面的高度是2m
8.已知抛物线y=(a+1)x2﹣ax﹣8过点(2,﹣2),且与x轴的一个交点的横坐标为2n,则代数式4n2﹣n+2020的值为( )
A.2024
B.2023
C.2022
D.2021
9.二次函数y=﹣x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )
A.t>﹣5
B.﹣5<t<3
C.3<t≤4
D.﹣5<t≤4
10.如图,抛物线y1=ax2+bx+c(a≠0)的顶点坐标A(﹣1,3),与x轴的一个交点B(﹣4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a﹣b=0;
②abc<0;
③抛物线与x轴的另一个交点坐标是(3,0);
④方程ax2+bx+c﹣3=0有两个相等的实数根;
⑤当﹣4<x<﹣1时,则y2<y1.其中正确的是( )
A.①②③
B.①③⑤
C.①④⑤
D.②③④
11.生产季节性产品的企业,当它的产品无利润或亏损时就会及时停产,某公司生产季节性产品,一年中第n月获得的利润y和对应月份n之间的函数表达式为y=﹣n2+12n﹣11,则该公司一年12个月中应停产的所有月份是( )
A.6
B.1,11
C.1,6,11
D.1,11,12
12.如图,抛物线y=ax2+bx+c(a≠0)与x轴一个交点为(﹣2,0),对称轴为直线x=1,则y<0时x的范围是( )
A.x>4或x<﹣2
B.﹣2<x<4
C.﹣2<x<3
D.0<x<3
13.在同一坐标系下,抛物线y1=﹣x2+4x和直线y2=2x的图象如图所示,那么不等式﹣x2+4x>2x的解集是( )
A.x<0
B.0<x<2
C.x>2
D.x<0或
x>2
14.已知二次函数y=ax2+bx+c的图象上部分点的横坐标x与纵坐标y的对应值如下表:
x
…
﹣1
0
1
2
…
y
…
0
3
4
3
…
那么关于它的图象,下列判断正确的是( )
A.开口向上
B.与x轴的另一个交点是(3,0)
C.与y轴交于负半轴
D.在直线x=1的左侧部分是下降的
15.点A,B的坐标分别为(﹣2,3)和(1,3),抛物线y=ax2+bx+c(a<0)的顶点在线段AB上运动时,形状保持不变,且与x轴交于C,D两点(C在D的左侧),给出下列结论:①c<3;②当x<﹣3时,y随x的增大而增大;③若点D的横坐标最大值为5,则点C的横坐标最小值为﹣5;④当四边形ACDB为平行四边形时,.其中正确的是( )
A.②④
B.②③
C.①③④
D.①②④
16.某工厂2020年产品的产量为100吨,该产品产量的年平均增长率为x(x>0),设2022年该产品的产量为y吨,则y关于x的函数关系式为( )
A.y=100(1﹣x)2
B.y=100(1+x)2
C.y=
D.y=100+100(1+x)+100(1+x)2
17.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=﹣1,点B的坐标为(1,0),则下列结论:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
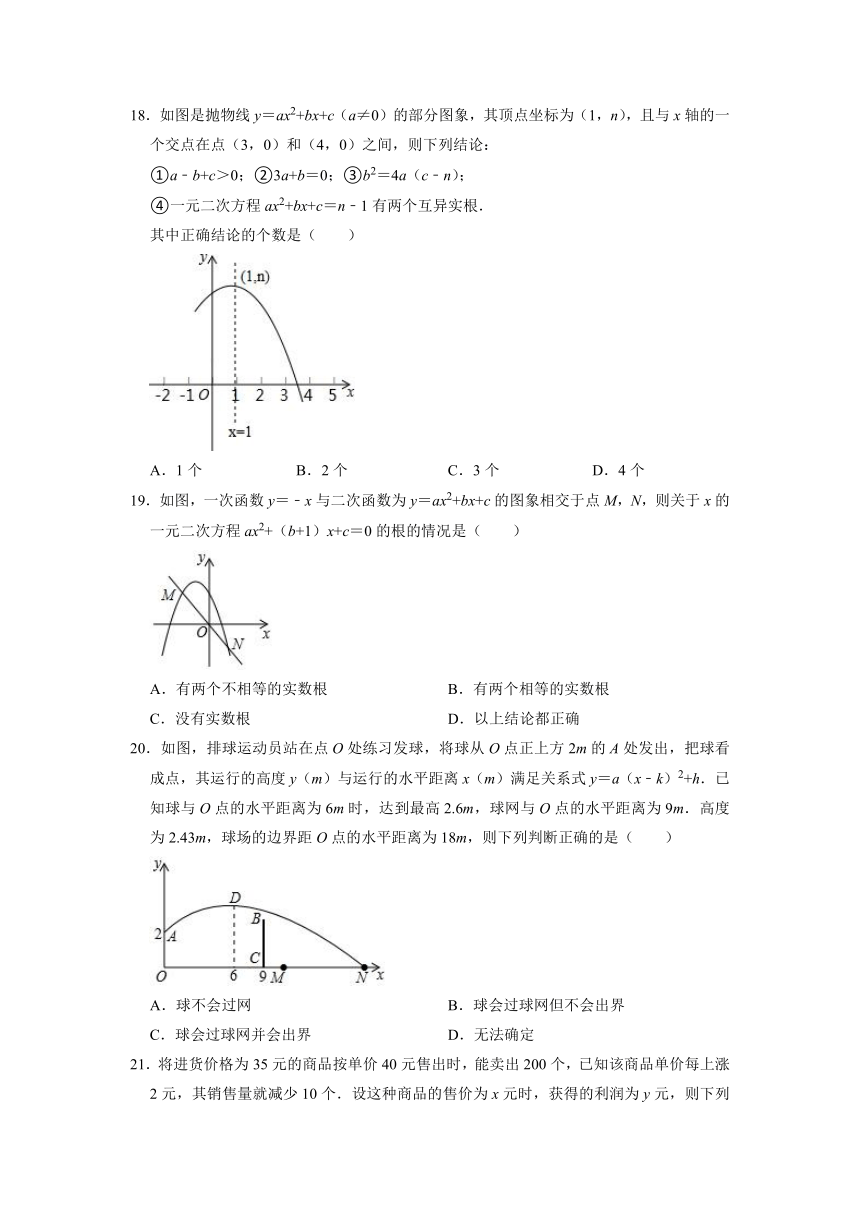
18.如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,则下列结论:
①a﹣b+c>0;②3a+b=0;③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个互异实根.
其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
19.如图,一次函数y=﹣x与二次函数为y=ax2+bx+c的图象相交于点M,N,则关于x的一元二次方程ax2+(b+1)x+c=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.以上结论都正确
20.如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣k)2+h.已知球与O点的水平距离为6m时,达到最高2.6m,球网与O点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
A.球不会过网
B.球会过球网但不会出界
C.球会过球网并会出界
D.无法确定
21.将进货价格为35元的商品按单价40元售出时,能卖出200个,已知该商品单价每上涨2元,其销售量就减少10个.设这种商品的售价为x元时,获得的利润为y元,则下列关系式正确的是( )
A.y=(x﹣35)(400﹣5x)
B.y=(x﹣35)(600﹣10x)
C.y=(x+5)(200﹣5x)
D.y=(x+5)(200﹣10x)
参考答案
1.解:抛物线对称轴为直线x=﹣故①正确;
当x=0时,y=2n﹣1故②错误;
把A点坐标(﹣1,2)代入抛物线解析式
得:2=m+4m+2n﹣1
整理得:2n=3﹣5m
代入y1=mx2﹣4mx+2n﹣1
整理得:y1=mx2﹣4mx+2﹣5m
由图象可知,抛物线交y轴于负半轴,
则:2﹣5m<0
即m>故③正确;
由抛物线的对称性,点B坐标为(5,2)
当y2=ax2的图象分别过点A、B时,其与线段分别有两个和有唯一一个公共点
此时,a的值分别为a=2、a=
a的取值范围是≤a<2;故④正确;
无论y1的图象向上平移1个单位后与x轴有无交点,在不等式大于0的解作为C1自变量的取值范围,对应的函数值都有正有负,故⑤错误.;
故选:B.
2.解:A、当t=9时,h=136;当t=13时,h=144;所以点火后9s和点火后13s的升空高度不相同,此选项错误;
B、当t=24时h=1≠0,所以点火后24s火箭离地面的高度为1m,此选项错误;
C、当t=10时h=141m,此选项错误;
D、由h=﹣t2+24t+1=﹣(t﹣12)2+145知火箭升空的最大高度为145m,此选项正确;
故选:D.
3.解:抛物线解析式为y=a(x+1)(x﹣3),
即y=ax2﹣2ax﹣3a,
∵y=a(x﹣1)2﹣4a,
∴当x=1时,二次函数有最小值﹣4a,所以①正确;
当x=4时,y=a?5?1=5a,
∴当﹣1≤x2≤4,则﹣4a≤y2≤5a,所以②错误;
∵点C(4,5a)关于直线x=1的对称点为(﹣2,5a),
∴当y2>y1,则x2>4或x<﹣2,所以③错误;
∵b=﹣2a,c=﹣3a,
∴方程cx2+bx+a=0化为﹣3ax2﹣2ax+a=0,
整理得3x2+2x﹣1=0,解得x1=﹣1,x2=,所以④正确.
故选:B.
4.解:①∵抛物线过点(﹣1,0),对称轴在y轴右侧,
∴当x=1时y>0,结论①错误;
②过点(0,2)作x轴的平行线,如图所示.
∵该直线与抛物线有两个交点,
∴方程ax2+bx+c=2有两个不相等的实数根,结论②正确;
③∵当x=1时y=a+b+c>0,
∴a+b>﹣c.
∵抛物线y=ax2+bx+c(a,b,c为常数,a≠0)经过点(0,3),
∴c=3,
∴a+b>﹣3.
∵当x=﹣1时,y=0,即a﹣b+c=0,
∴b=a+c,
∴a+b=2a+c.
∵抛物线开口向下,
∴a<0,
∴a+b<c=3,
∴﹣3<a+b<3,结论③正确.
故选:C.
5.解:抛物线y=ax2+2ax+m的对称轴为直线x=﹣=﹣1,
而抛物线与x轴的一个交点坐标为(2,0),
∴抛物线与x轴的另一个交点坐标为(﹣4,0),
∵a<0,
∴抛物线开口向下,
∴当x<﹣4或x>2时,y<0.
故选:A.
6.解:∵抛物线与y轴的交点在x轴上方,
∴c>0,
∵抛物线的对称轴为直线x=﹣=1,
∴b=﹣2a,
∴2a+b+c=2a﹣2a+c=c>0,所以①正确;
∵抛物线与x轴的一个交点在点(3,0)左侧,
而抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点在点(﹣1,0)右侧,
∴当x=﹣1时,y<0,
∴a﹣b+c<0,所以②正确;
∵x=1时,二次函数有最大值,
∴ax2+bx+c≤a+b+c,
∴ax2+bx≤a+b,所以③正确;
∵直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,
∴x=3时,一次函数值比二次函数值大,
即9a+3b+c<﹣3+c,
而b=﹣2a,
∴9a﹣6a<﹣3,解得a<﹣1,所以④正确.
故选:A.
7.解:A、∵抛物线的顶点坐标为(0,3.5),
∴可设抛物线的函数关系式为y=ax2+3.5.
∵篮圈中心(1.5,3.05)在抛物线上,将它的坐标代入上式,得
3.05=a×1.52+3.5,
∴a=﹣,
∴y=﹣x2+3.5.
故本选项正确;
B、由图示知,篮圈中心的坐标是(1.5,3.05),
故本选项错误;
C、由图示知,此抛物线的顶点坐标是(0,3.5),
故本选项错误;
D、设这次跳投时,球出手处离地面hm,
因为(1)中求得y=﹣0.2x2+3.5,
∴当x=﹣2.5时,
h=﹣0.2×(﹣2.5)2+3.5=2.25(m).
∴这次跳投时,球出手处离地面2.25m.
故本选项错误.
故选:A.
8.解:∵抛物线y=(a+1)x2﹣ax﹣8过点(2,﹣2),
∴﹣2=(a+1)×22﹣a×2﹣8=2a﹣4,
解得,a=1,
∴y=2x2﹣x﹣8,
∵抛物线y=2x2﹣x﹣8与x轴的一个交点的横坐标为2n,
∴2×(2n)2﹣2n﹣8=0,
化简,得
4n2﹣n﹣4=0,
∴4n2﹣n=4,
∴4n2﹣n+2020=4+2020=2024,
故选:A.
9.解:如图,关于x的一元二次方程﹣x2+mx﹣t=0的解就是抛物线y=﹣x2+mx与直线y=t的交点的横坐标,由题意可知:m=4,
当x=1时,y=3,
当x=5时,y=﹣5,
由图象可知关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,
直线y=t在直线y=﹣5和直线y=4之间包括直线y=4,
∴﹣5<t≤4.
故选:D.
10.解:∵抛物线的顶点坐标A(﹣1,3),
∴抛物线的对称轴为直线x=﹣=﹣1,
∴2a﹣b=0,所以①正确;
∵抛物线开口向下,
∴a<0,
∴b=2a<0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc>0,所以②错误;
∵抛物线与x轴的一个交点为(﹣4,0)
而抛物线的对称轴为直线x=﹣1,
∴抛物线与x轴的另一个交点为(2,0),所以③错误;
∵抛物线的顶点坐标A(﹣1,3),
∴x=﹣1时,二次函数有最大值,
∴方程ax2+bx+c=3有两个相等的实数根,所以④正确;
∵抛物线y1=ax2+bx+c与直线y2=mx+n(m≠0)交于A(﹣1,3),B点(﹣4,0)
∴当﹣4<x<﹣1时,y2<y1,所以⑤正确.
故选:C.
11.解:由题意知,
利润y和月份n之间函数关系式为y=﹣n2+12n﹣11,
∴y=﹣(n﹣6)2+25,
当n=1时,y=0,
当n=11时,y=0,
当n=12时,y<0,
故停产的月份是1月、11月、12月.
故选:D.
12.解:∵y=ax2+bx+c的对称轴为直线x=1,与x轴的一个交点为(﹣2,0),
∴抛物线与x轴的另一个交点为(4,0),
∴y<0时x的范围是﹣2<x<4,
故选:B.
13.解:由图可知,抛物线y1=﹣x2+4x和直线y2=2x的交点坐标为(0,0),(2,4),
所以,不等式﹣x2+4x>2x的解集是0<x<2.
故选:B.
14.解:A、由表格知,抛物线的顶点坐标是(1,4).故设抛物线解析式为y=a(x﹣1)2+4.
将(﹣1,0)代入,得
a(﹣1﹣1)2+4=0,
解得a=﹣1.
∵a=﹣1<0,
∴抛物线的开口方向向下,
故本选项错误;
B、抛物线与x轴的一个交点为(﹣1,0),对称轴是直线x=1,则抛物线与x轴的另一个交点是(3,0),故本选项正确;
C、由表格知,抛物线与y轴的交点坐标是(0,3),即与y轴交于正半轴,故本选项错误;
D、抛物线开口方向向下,对称轴为直线x=1,则在直线x=1的左侧部分是上升的,故本选项错误;
故选:B.
15.解:∵点A,B的坐标分别为(﹣2,3)和(1,3),
∴线段AB与y轴的交点坐标为(0,3),
又∵抛物线的顶点在线段AB上运动,抛物线与y轴的交点坐标为(0,c),
∴c≤3,(顶点在y轴上时取“=”),故①错误;
∵抛物线的顶点在线段AB上运动,
∴当x<﹣2时,y随x的增大而增大,
因此,当x<﹣3时,y随x的增大而增大,故②正确;
若点D的横坐标最大值为5,则此时对称轴为直线x=1,
根据二次函数的对称性,点C的横坐标最小值为﹣2﹣4=﹣6,故③错误;
根据顶点坐标公式,=3,
令y=0,则ax2+bx+c=0,
CD2=(﹣)2﹣4×=,
根据顶点坐标公式,=3,
∴=﹣12,
∴CD2=×(﹣12)=,
∵四边形ACDB为平行四边形,
∴CD=AB=1﹣(﹣2)=3,
∴=32=9,
解得a=﹣,故④正确;
综上所述,正确的结论有②④.
故选:A.
16.解:根据题意,得:y关于x的函数关系式为y=100(1+x)2,
故选:B.
17.解:∵抛物线的对称轴为直线x=﹣1,点B的坐标为(1,0),
∴A(﹣3,0),
∴AB=1﹣(﹣3)=4,所以①正确;
∵抛物线与x轴有2个交点,
∴Δ=b2﹣4ac>0,所以②正确;
∵抛物线开口向下,
∴a>0,
∵抛物线的对称轴为直线x=﹣=﹣1,
∴b=2a>0,
∴ab>0,所以③错误;
∵x=﹣1时,y<0,
∴a﹣b+c<0,
而a>0,
∴a(a﹣b+c)<0,所以④正确.
故选:C.
18.解:∵抛物线与x轴的一个交点在点(3,0)和(4,0)之间,而抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点在点(﹣2,0)和(﹣1,0)之间.
∴当x=﹣1时,y>0,
即a﹣b+c>0,所以①正确;
∵抛物线的对称轴为直线x=﹣=1,即b=﹣2a,
∴3a+b=3a﹣2a=a,所以②错误;
∵抛物线的顶点坐标为(1,n),
∴=n,
∴b2=4ac﹣4an=4a(c﹣n),所以③正确;
∵抛物线与直线y=n有一个公共点,
∴抛物线与直线y=n﹣1有2个公共点,
∴一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根,所以④正确.
故选:C.
19.解:∵一次函数y=﹣x与二次函数为y=ax2+bx+c的图象有两个交点,
∴ax2+bx+c=﹣x有两个不相等的实数根,
ax2+bx+c=﹣x变形为ax2+(b+1)x+c=0,
∴ax2+(b+1)x+c=0有两个不相等的实数根,
故选:A.
20.解:∵球与O点的水平距离为6m时,达到最高2.6m,
∴抛物线为y=a(x﹣6)2+2.6过点,
∵抛物线y=a(x﹣6)2+2.6过点(0,2),
∴2=a(0﹣6)2+2.6,
解得:a=﹣,
故y与x的关系式为:y=﹣(x﹣6)2+2.6,
当x=9时,y=﹣(x﹣6)2+2.6=2.45>2.43,
所以球能过球网;
当y=0时,﹣(x﹣6)2+2.6=0,
解得:x1=6+2>18,x2=6﹣2(舍去)
故会出界.
故选:C.
21.解:设这种商品的售价为x元时,获得的利润为y元,根据题意可得:y=(x﹣35)(400﹣5x),
故选:A.
1.抛物线C1:y1=mx2﹣4mx+2n﹣1与平行于x轴的直线交于A、B两点,且A点坐标为(﹣1,2),请结合图象分析以下结论:①对称轴为直线x=2;②抛物线与y轴交点坐标为(0,﹣1);③m>;④若抛物线C2:y2=ax2(a≠0)与线段AB恰有一个公共点,则a的取值范围是≤a<2;⑤不等式mx2﹣4mx+2n>0的解作为函数C1的自变量的取值时,对应的函数值均为正数,其中正确结论的个数有( )
A.2个
B.3个
C.4个
D.5个
2.已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1.则下列说法中正确的是( )
A.点火后9s和点火后13s的升空高度相同
B.点火后24s火箭落于地面
C.点火后10s的升空高度为139m
D.火箭升空的最大高度为145m
3.如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和
其中正确结论的个数是( )
A.1
B.2
C.3
D.4
4.已知抛物线y=ax2+bx+c(a,b,c为常数,a≠0)经过点(﹣1,0),(0,3),其对称轴在y轴右侧.有下列结论:
①抛物线经过点(1,0);②方程ax2+bx+c=2有两个不相等的实数根;
③﹣3<a+b<3其中,正确结论的个数为( )
A.0
B.1
C.2
D.3
5.函数y=ax2+2ax+m(a<0)的图象过点(2,0),则使函数值y<0成立的x的取值范围是( )
A.x<﹣4或x>2
B.﹣4<x<2
C.x<0或x>2
D.0<x<2
6.如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:
①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.其中正确的有( )
A.4个
B.3个
C.2个
D.1个
7.一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮筐内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是( )
A.此抛物线的解析式是y=﹣x2+3.5
B.篮圈中心的坐标是(4,3.05)
C.此抛物线的顶点坐标是(3.5,0)
D.篮球出手时离地面的高度是2m
8.已知抛物线y=(a+1)x2﹣ax﹣8过点(2,﹣2),且与x轴的一个交点的横坐标为2n,则代数式4n2﹣n+2020的值为( )
A.2024
B.2023
C.2022
D.2021
9.二次函数y=﹣x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )
A.t>﹣5
B.﹣5<t<3
C.3<t≤4
D.﹣5<t≤4
10.如图,抛物线y1=ax2+bx+c(a≠0)的顶点坐标A(﹣1,3),与x轴的一个交点B(﹣4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a﹣b=0;
②abc<0;
③抛物线与x轴的另一个交点坐标是(3,0);
④方程ax2+bx+c﹣3=0有两个相等的实数根;
⑤当﹣4<x<﹣1时,则y2<y1.其中正确的是( )
A.①②③
B.①③⑤
C.①④⑤
D.②③④
11.生产季节性产品的企业,当它的产品无利润或亏损时就会及时停产,某公司生产季节性产品,一年中第n月获得的利润y和对应月份n之间的函数表达式为y=﹣n2+12n﹣11,则该公司一年12个月中应停产的所有月份是( )
A.6
B.1,11
C.1,6,11
D.1,11,12
12.如图,抛物线y=ax2+bx+c(a≠0)与x轴一个交点为(﹣2,0),对称轴为直线x=1,则y<0时x的范围是( )
A.x>4或x<﹣2
B.﹣2<x<4
C.﹣2<x<3
D.0<x<3
13.在同一坐标系下,抛物线y1=﹣x2+4x和直线y2=2x的图象如图所示,那么不等式﹣x2+4x>2x的解集是( )
A.x<0
B.0<x<2
C.x>2
D.x<0或
x>2
14.已知二次函数y=ax2+bx+c的图象上部分点的横坐标x与纵坐标y的对应值如下表:
x
…
﹣1
0
1
2
…
y
…
0
3
4
3
…
那么关于它的图象,下列判断正确的是( )
A.开口向上
B.与x轴的另一个交点是(3,0)
C.与y轴交于负半轴
D.在直线x=1的左侧部分是下降的
15.点A,B的坐标分别为(﹣2,3)和(1,3),抛物线y=ax2+bx+c(a<0)的顶点在线段AB上运动时,形状保持不变,且与x轴交于C,D两点(C在D的左侧),给出下列结论:①c<3;②当x<﹣3时,y随x的增大而增大;③若点D的横坐标最大值为5,则点C的横坐标最小值为﹣5;④当四边形ACDB为平行四边形时,.其中正确的是( )
A.②④
B.②③
C.①③④
D.①②④
16.某工厂2020年产品的产量为100吨,该产品产量的年平均增长率为x(x>0),设2022年该产品的产量为y吨,则y关于x的函数关系式为( )
A.y=100(1﹣x)2
B.y=100(1+x)2
C.y=
D.y=100+100(1+x)+100(1+x)2
17.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=﹣1,点B的坐标为(1,0),则下列结论:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
18.如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,则下列结论:
①a﹣b+c>0;②3a+b=0;③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个互异实根.
其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
19.如图,一次函数y=﹣x与二次函数为y=ax2+bx+c的图象相交于点M,N,则关于x的一元二次方程ax2+(b+1)x+c=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.以上结论都正确
20.如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣k)2+h.已知球与O点的水平距离为6m时,达到最高2.6m,球网与O点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
A.球不会过网
B.球会过球网但不会出界
C.球会过球网并会出界
D.无法确定
21.将进货价格为35元的商品按单价40元售出时,能卖出200个,已知该商品单价每上涨2元,其销售量就减少10个.设这种商品的售价为x元时,获得的利润为y元,则下列关系式正确的是( )
A.y=(x﹣35)(400﹣5x)
B.y=(x﹣35)(600﹣10x)
C.y=(x+5)(200﹣5x)
D.y=(x+5)(200﹣10x)
参考答案
1.解:抛物线对称轴为直线x=﹣故①正确;
当x=0时,y=2n﹣1故②错误;
把A点坐标(﹣1,2)代入抛物线解析式
得:2=m+4m+2n﹣1
整理得:2n=3﹣5m
代入y1=mx2﹣4mx+2n﹣1
整理得:y1=mx2﹣4mx+2﹣5m
由图象可知,抛物线交y轴于负半轴,
则:2﹣5m<0
即m>故③正确;
由抛物线的对称性,点B坐标为(5,2)
当y2=ax2的图象分别过点A、B时,其与线段分别有两个和有唯一一个公共点
此时,a的值分别为a=2、a=
a的取值范围是≤a<2;故④正确;
无论y1的图象向上平移1个单位后与x轴有无交点,在不等式大于0的解作为C1自变量的取值范围,对应的函数值都有正有负,故⑤错误.;
故选:B.
2.解:A、当t=9时,h=136;当t=13时,h=144;所以点火后9s和点火后13s的升空高度不相同,此选项错误;
B、当t=24时h=1≠0,所以点火后24s火箭离地面的高度为1m,此选项错误;
C、当t=10时h=141m,此选项错误;
D、由h=﹣t2+24t+1=﹣(t﹣12)2+145知火箭升空的最大高度为145m,此选项正确;
故选:D.
3.解:抛物线解析式为y=a(x+1)(x﹣3),
即y=ax2﹣2ax﹣3a,
∵y=a(x﹣1)2﹣4a,
∴当x=1时,二次函数有最小值﹣4a,所以①正确;
当x=4时,y=a?5?1=5a,
∴当﹣1≤x2≤4,则﹣4a≤y2≤5a,所以②错误;
∵点C(4,5a)关于直线x=1的对称点为(﹣2,5a),
∴当y2>y1,则x2>4或x<﹣2,所以③错误;
∵b=﹣2a,c=﹣3a,
∴方程cx2+bx+a=0化为﹣3ax2﹣2ax+a=0,
整理得3x2+2x﹣1=0,解得x1=﹣1,x2=,所以④正确.
故选:B.
4.解:①∵抛物线过点(﹣1,0),对称轴在y轴右侧,
∴当x=1时y>0,结论①错误;
②过点(0,2)作x轴的平行线,如图所示.
∵该直线与抛物线有两个交点,
∴方程ax2+bx+c=2有两个不相等的实数根,结论②正确;
③∵当x=1时y=a+b+c>0,
∴a+b>﹣c.
∵抛物线y=ax2+bx+c(a,b,c为常数,a≠0)经过点(0,3),
∴c=3,
∴a+b>﹣3.
∵当x=﹣1时,y=0,即a﹣b+c=0,
∴b=a+c,
∴a+b=2a+c.
∵抛物线开口向下,
∴a<0,
∴a+b<c=3,
∴﹣3<a+b<3,结论③正确.
故选:C.
5.解:抛物线y=ax2+2ax+m的对称轴为直线x=﹣=﹣1,
而抛物线与x轴的一个交点坐标为(2,0),
∴抛物线与x轴的另一个交点坐标为(﹣4,0),
∵a<0,
∴抛物线开口向下,
∴当x<﹣4或x>2时,y<0.
故选:A.
6.解:∵抛物线与y轴的交点在x轴上方,
∴c>0,
∵抛物线的对称轴为直线x=﹣=1,
∴b=﹣2a,
∴2a+b+c=2a﹣2a+c=c>0,所以①正确;
∵抛物线与x轴的一个交点在点(3,0)左侧,
而抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点在点(﹣1,0)右侧,
∴当x=﹣1时,y<0,
∴a﹣b+c<0,所以②正确;
∵x=1时,二次函数有最大值,
∴ax2+bx+c≤a+b+c,
∴ax2+bx≤a+b,所以③正确;
∵直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,
∴x=3时,一次函数值比二次函数值大,
即9a+3b+c<﹣3+c,
而b=﹣2a,
∴9a﹣6a<﹣3,解得a<﹣1,所以④正确.
故选:A.
7.解:A、∵抛物线的顶点坐标为(0,3.5),
∴可设抛物线的函数关系式为y=ax2+3.5.
∵篮圈中心(1.5,3.05)在抛物线上,将它的坐标代入上式,得
3.05=a×1.52+3.5,
∴a=﹣,
∴y=﹣x2+3.5.
故本选项正确;
B、由图示知,篮圈中心的坐标是(1.5,3.05),
故本选项错误;
C、由图示知,此抛物线的顶点坐标是(0,3.5),
故本选项错误;
D、设这次跳投时,球出手处离地面hm,
因为(1)中求得y=﹣0.2x2+3.5,
∴当x=﹣2.5时,
h=﹣0.2×(﹣2.5)2+3.5=2.25(m).
∴这次跳投时,球出手处离地面2.25m.
故本选项错误.
故选:A.
8.解:∵抛物线y=(a+1)x2﹣ax﹣8过点(2,﹣2),
∴﹣2=(a+1)×22﹣a×2﹣8=2a﹣4,
解得,a=1,
∴y=2x2﹣x﹣8,
∵抛物线y=2x2﹣x﹣8与x轴的一个交点的横坐标为2n,
∴2×(2n)2﹣2n﹣8=0,
化简,得
4n2﹣n﹣4=0,
∴4n2﹣n=4,
∴4n2﹣n+2020=4+2020=2024,
故选:A.
9.解:如图,关于x的一元二次方程﹣x2+mx﹣t=0的解就是抛物线y=﹣x2+mx与直线y=t的交点的横坐标,由题意可知:m=4,
当x=1时,y=3,
当x=5时,y=﹣5,
由图象可知关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,
直线y=t在直线y=﹣5和直线y=4之间包括直线y=4,
∴﹣5<t≤4.
故选:D.
10.解:∵抛物线的顶点坐标A(﹣1,3),
∴抛物线的对称轴为直线x=﹣=﹣1,
∴2a﹣b=0,所以①正确;
∵抛物线开口向下,
∴a<0,
∴b=2a<0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc>0,所以②错误;
∵抛物线与x轴的一个交点为(﹣4,0)
而抛物线的对称轴为直线x=﹣1,
∴抛物线与x轴的另一个交点为(2,0),所以③错误;
∵抛物线的顶点坐标A(﹣1,3),
∴x=﹣1时,二次函数有最大值,
∴方程ax2+bx+c=3有两个相等的实数根,所以④正确;
∵抛物线y1=ax2+bx+c与直线y2=mx+n(m≠0)交于A(﹣1,3),B点(﹣4,0)
∴当﹣4<x<﹣1时,y2<y1,所以⑤正确.
故选:C.
11.解:由题意知,
利润y和月份n之间函数关系式为y=﹣n2+12n﹣11,
∴y=﹣(n﹣6)2+25,
当n=1时,y=0,
当n=11时,y=0,
当n=12时,y<0,
故停产的月份是1月、11月、12月.
故选:D.
12.解:∵y=ax2+bx+c的对称轴为直线x=1,与x轴的一个交点为(﹣2,0),
∴抛物线与x轴的另一个交点为(4,0),
∴y<0时x的范围是﹣2<x<4,
故选:B.
13.解:由图可知,抛物线y1=﹣x2+4x和直线y2=2x的交点坐标为(0,0),(2,4),
所以,不等式﹣x2+4x>2x的解集是0<x<2.
故选:B.
14.解:A、由表格知,抛物线的顶点坐标是(1,4).故设抛物线解析式为y=a(x﹣1)2+4.
将(﹣1,0)代入,得
a(﹣1﹣1)2+4=0,
解得a=﹣1.
∵a=﹣1<0,
∴抛物线的开口方向向下,
故本选项错误;
B、抛物线与x轴的一个交点为(﹣1,0),对称轴是直线x=1,则抛物线与x轴的另一个交点是(3,0),故本选项正确;
C、由表格知,抛物线与y轴的交点坐标是(0,3),即与y轴交于正半轴,故本选项错误;
D、抛物线开口方向向下,对称轴为直线x=1,则在直线x=1的左侧部分是上升的,故本选项错误;
故选:B.
15.解:∵点A,B的坐标分别为(﹣2,3)和(1,3),
∴线段AB与y轴的交点坐标为(0,3),
又∵抛物线的顶点在线段AB上运动,抛物线与y轴的交点坐标为(0,c),
∴c≤3,(顶点在y轴上时取“=”),故①错误;
∵抛物线的顶点在线段AB上运动,
∴当x<﹣2时,y随x的增大而增大,
因此,当x<﹣3时,y随x的增大而增大,故②正确;
若点D的横坐标最大值为5,则此时对称轴为直线x=1,
根据二次函数的对称性,点C的横坐标最小值为﹣2﹣4=﹣6,故③错误;
根据顶点坐标公式,=3,
令y=0,则ax2+bx+c=0,
CD2=(﹣)2﹣4×=,
根据顶点坐标公式,=3,
∴=﹣12,
∴CD2=×(﹣12)=,
∵四边形ACDB为平行四边形,
∴CD=AB=1﹣(﹣2)=3,
∴=32=9,
解得a=﹣,故④正确;
综上所述,正确的结论有②④.
故选:A.
16.解:根据题意,得:y关于x的函数关系式为y=100(1+x)2,
故选:B.
17.解:∵抛物线的对称轴为直线x=﹣1,点B的坐标为(1,0),
∴A(﹣3,0),
∴AB=1﹣(﹣3)=4,所以①正确;
∵抛物线与x轴有2个交点,
∴Δ=b2﹣4ac>0,所以②正确;
∵抛物线开口向下,
∴a>0,
∵抛物线的对称轴为直线x=﹣=﹣1,
∴b=2a>0,
∴ab>0,所以③错误;
∵x=﹣1时,y<0,
∴a﹣b+c<0,
而a>0,
∴a(a﹣b+c)<0,所以④正确.
故选:C.
18.解:∵抛物线与x轴的一个交点在点(3,0)和(4,0)之间,而抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点在点(﹣2,0)和(﹣1,0)之间.
∴当x=﹣1时,y>0,
即a﹣b+c>0,所以①正确;
∵抛物线的对称轴为直线x=﹣=1,即b=﹣2a,
∴3a+b=3a﹣2a=a,所以②错误;
∵抛物线的顶点坐标为(1,n),
∴=n,
∴b2=4ac﹣4an=4a(c﹣n),所以③正确;
∵抛物线与直线y=n有一个公共点,
∴抛物线与直线y=n﹣1有2个公共点,
∴一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根,所以④正确.
故选:C.
19.解:∵一次函数y=﹣x与二次函数为y=ax2+bx+c的图象有两个交点,
∴ax2+bx+c=﹣x有两个不相等的实数根,
ax2+bx+c=﹣x变形为ax2+(b+1)x+c=0,
∴ax2+(b+1)x+c=0有两个不相等的实数根,
故选:A.
20.解:∵球与O点的水平距离为6m时,达到最高2.6m,
∴抛物线为y=a(x﹣6)2+2.6过点,
∵抛物线y=a(x﹣6)2+2.6过点(0,2),
∴2=a(0﹣6)2+2.6,
解得:a=﹣,
故y与x的关系式为:y=﹣(x﹣6)2+2.6,
当x=9时,y=﹣(x﹣6)2+2.6=2.45>2.43,
所以球能过球网;
当y=0时,﹣(x﹣6)2+2.6=0,
解得:x1=6+2>18,x2=6﹣2(舍去)
故会出界.
故选:C.
21.解:设这种商品的售价为x元时,获得的利润为y元,根据题意可得:y=(x﹣35)(400﹣5x),
故选:A.
同课章节目录
