3.3.1解析算法及其程序实现 课件(22ppt)
文档属性
| 名称 | 3.3.1解析算法及其程序实现 课件(22ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2021-08-26 13:48:50 | ||
图片预览







文档简介
(共22张PPT)
解析算法及其程序实现
第
三
单
元
第
三
单
元
3.3.1
目录
目录
01
01
复习回顾
02
02
案例分析
03
03
实战演练
04
04
小结
https://www./
1
抽象与建模
从显示项目的真实情景中提炼出核心的要素并加以确定或假设,最终定义出一个有明确已知条件和求解的目标的题目,并用数学符号描述该问题的计算模型
2
设计算法\描述算法
遵循算法的特征、围绕算法的要素设计算法,涉及太多条件时可使用流程图来进一步描述解决该问题的算法
复习回顾
复习回顾
3
编写算法
根据流程图编写代码
还记得我们在3.1节学习的计算机解决实际问题的算法吗?
4
调试运行程序
运行程序,计算机抛出错误后加以修正
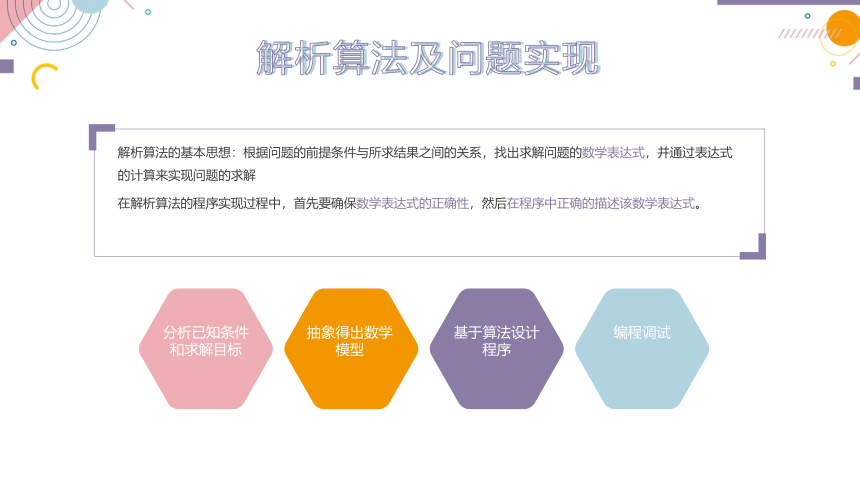
解析算法及问题实现
解析算法及问题实现
抽象得出数学模型
分析已知条件和求解目标
基于算法设计程序
编程调试
解析算法的基本思想:根据问题的前提条件与所求结果之间的关系,找出求解问题的数学表达式,并通过表达式的计算来实现问题的求解
在解析算法的程序实现过程中,首先要确保数学表达式的正确性,然后在程序中正确的描述该数学表达式。
案例分析
案例分析
如图所示答题卡常用于标准化考试、选举和调查。答题卡一般采用2B铅笔填图,填涂好的答题卡经过扫描后得到相应的数字化图像,再通过光学识别,完成答题卡信息数据的采集、分析与统计。那么计算机是如何判断答题卡中哪些信息点被填涂了呢?
————————————————————————
案例分析
案例分析
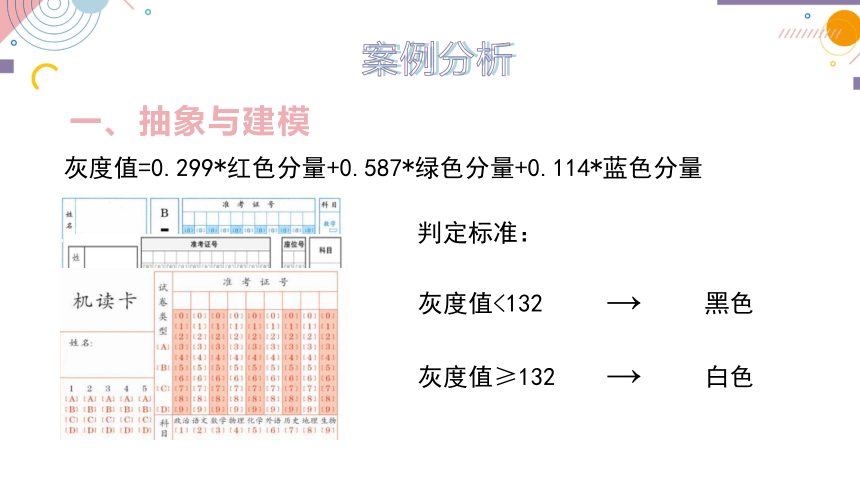
一、抽象与建模
灰度值=0.299
红色分量+0.587
绿色分量+0.114
蓝色分量
判定标准:
灰度值<132
→
黑色
灰度值≥132
→
白色
案例分析
案例分析
二、设计算法
1
给定颜色初值
输入某像素在RGB颜色模式下的各个颜色分量
2
转换颜色模式
将彩色(RGB颜色模式)值转化成灰度值
3
判定黑白颜色
若灰度值小于132,则判定为黑色;否则判定为白色
案例分析
案例分析
三、编写程序
R=43
G=10
B=241
Gray_scale=0.299
R+0.587
G+0.114
B
if
Gray_scale<132:
print(“黑色”)
else:
print(“白色”)
解释器界面:
①
②
实战演练
实战演练
1.某地区为了开发山区农业,需要了解山地的气候变化。现已知该山地海拔每升高100m,气温下降约0.5℃,山地最高海拔为1500m,山脚下的年平均气温为22℃(假设山脚海拔为0m)
根据气温随海拔升高而变化的规律,写出计算该山地不同海拔高度的气温解析式,并编程实现
分析:
①海拔升高100m,温度下降0.5℃
②最高海拔1500m,山脚平均气温22℃
实战演练
实战演练
一、抽象与建模
0≤h≤1500
t变化=h÷100×0.5
th=22-h÷100×0.5
实战演练
实战演练
二、设计算法
输入海拔h
t=22-h/100
5
输出温度t
结束
开始
三、编写程序
h=int(input("请输入山地海拔:"))
t=22-h/100
0.5
print(t)
解释器界面:
实战演练
实战演练
实战演练
实战演练
1.某地区为了开发山区农业,需要了解山地的气候变化。现已知该山地海拔每升高100m,气温下降约0.5℃,山地最高海拔为1500m,山脚下的年平均气温为22℃(假设山脚海拔为0m)
某种植物适宜生长在气温为18℃-20℃的山区,如果要分析这种植物应该被种植在山地多高的地区为宜,需要如何修改算法,请编程实现
分析:
①种植物适宜生长在气温为18℃-20℃
②t=22-h/100
0.5
实战演练
实战演练
一、抽象与建模
0≤h≤1500
h=(22-th)×100×2
实战演练
实战演练
二、设计算法
t1=18,t2=20
h1=(22-t1)×100×2
输出h1、h2
结束
开始
h2=(22-t2)×100×2
三、编写程序
t1=18
t2=20
h1=(22-t1)
100
2
h2=(22-t2)
100
2
print("植物适宜生长的海拔区间:",h2,h1)
解释器界面:
实战演练
实战演练
实战演练
实战演练
平地上整齐的铺满了边长为1分米的正方形砖块,以某四块砖的交点为圆心,画一个半径为r(r≤4√2)分米的圆,计算圆内所能包含的砖块数量。
分析:
①中心对称
③砖块有i=int(r)行/列
②累加每行砖块数
实战演练
实战演练
一、抽象与建模
r
第i列
di
d=d1+d2+......+dint(r)
=
)
+
......+
i为整数
=
实战演练
实战演练
二、设计算法
1
给定半径,每列砖块数初值
输入半径r(r≤4√2),每列砖块数d
2
计算并累加每行砖块数
计算每行砖块数并且存入d,再计算下一行并且累加到d上
3
计算整个圆的砖块数
总量sum等于d的四倍
三、编写程序
r=32
0.5
d=0
sum=0
for
i
in
range(1,int(r)+1,1):
d=d+int((r
2-i
2)
0.5)
sum=d
4
print(sum)
解释器界面:
实战演练
实战演练
①
②
1、分析已知已知条件和求解目标
2、抽象得出数学模型
3、代入数值求解
解析算法
1、分析问题
2、抽象建模
3、基于解析算法设计程序
4、编程调试
基于解析算法的问题解决
小结
小结
作业
作业
解析算法及其程序实现
第
三
单
元
第
三
单
元
3.3.1
目录
目录
01
01
复习回顾
02
02
案例分析
03
03
实战演练
04
04
小结
https://www./
1
抽象与建模
从显示项目的真实情景中提炼出核心的要素并加以确定或假设,最终定义出一个有明确已知条件和求解的目标的题目,并用数学符号描述该问题的计算模型
2
设计算法\描述算法
遵循算法的特征、围绕算法的要素设计算法,涉及太多条件时可使用流程图来进一步描述解决该问题的算法
复习回顾
复习回顾
3
编写算法
根据流程图编写代码
还记得我们在3.1节学习的计算机解决实际问题的算法吗?
4
调试运行程序
运行程序,计算机抛出错误后加以修正
解析算法及问题实现
解析算法及问题实现
抽象得出数学模型
分析已知条件和求解目标
基于算法设计程序
编程调试
解析算法的基本思想:根据问题的前提条件与所求结果之间的关系,找出求解问题的数学表达式,并通过表达式的计算来实现问题的求解
在解析算法的程序实现过程中,首先要确保数学表达式的正确性,然后在程序中正确的描述该数学表达式。
案例分析
案例分析
如图所示答题卡常用于标准化考试、选举和调查。答题卡一般采用2B铅笔填图,填涂好的答题卡经过扫描后得到相应的数字化图像,再通过光学识别,完成答题卡信息数据的采集、分析与统计。那么计算机是如何判断答题卡中哪些信息点被填涂了呢?
————————————————————————
案例分析
案例分析
一、抽象与建模
灰度值=0.299
红色分量+0.587
绿色分量+0.114
蓝色分量
判定标准:
灰度值<132
→
黑色
灰度值≥132
→
白色
案例分析
案例分析
二、设计算法
1
给定颜色初值
输入某像素在RGB颜色模式下的各个颜色分量
2
转换颜色模式
将彩色(RGB颜色模式)值转化成灰度值
3
判定黑白颜色
若灰度值小于132,则判定为黑色;否则判定为白色
案例分析
案例分析
三、编写程序
R=43
G=10
B=241
Gray_scale=0.299
R+0.587
G+0.114
B
if
Gray_scale<132:
print(“黑色”)
else:
print(“白色”)
解释器界面:
①
②
实战演练
实战演练
1.某地区为了开发山区农业,需要了解山地的气候变化。现已知该山地海拔每升高100m,气温下降约0.5℃,山地最高海拔为1500m,山脚下的年平均气温为22℃(假设山脚海拔为0m)
根据气温随海拔升高而变化的规律,写出计算该山地不同海拔高度的气温解析式,并编程实现
分析:
①海拔升高100m,温度下降0.5℃
②最高海拔1500m,山脚平均气温22℃
实战演练
实战演练
一、抽象与建模
0≤h≤1500
t变化=h÷100×0.5
th=22-h÷100×0.5
实战演练
实战演练
二、设计算法
输入海拔h
t=22-h/100
5
输出温度t
结束
开始
三、编写程序
h=int(input("请输入山地海拔:"))
t=22-h/100
0.5
print(t)
解释器界面:
实战演练
实战演练
实战演练
实战演练
1.某地区为了开发山区农业,需要了解山地的气候变化。现已知该山地海拔每升高100m,气温下降约0.5℃,山地最高海拔为1500m,山脚下的年平均气温为22℃(假设山脚海拔为0m)
某种植物适宜生长在气温为18℃-20℃的山区,如果要分析这种植物应该被种植在山地多高的地区为宜,需要如何修改算法,请编程实现
分析:
①种植物适宜生长在气温为18℃-20℃
②t=22-h/100
0.5
实战演练
实战演练
一、抽象与建模
0≤h≤1500
h=(22-th)×100×2
实战演练
实战演练
二、设计算法
t1=18,t2=20
h1=(22-t1)×100×2
输出h1、h2
结束
开始
h2=(22-t2)×100×2
三、编写程序
t1=18
t2=20
h1=(22-t1)
100
2
h2=(22-t2)
100
2
print("植物适宜生长的海拔区间:",h2,h1)
解释器界面:
实战演练
实战演练
实战演练
实战演练
平地上整齐的铺满了边长为1分米的正方形砖块,以某四块砖的交点为圆心,画一个半径为r(r≤4√2)分米的圆,计算圆内所能包含的砖块数量。
分析:
①中心对称
③砖块有i=int(r)行/列
②累加每行砖块数
实战演练
实战演练
一、抽象与建模
r
第i列
di
d=d1+d2+......+dint(r)
=
)
+
......+
i为整数
=
实战演练
实战演练
二、设计算法
1
给定半径,每列砖块数初值
输入半径r(r≤4√2),每列砖块数d
2
计算并累加每行砖块数
计算每行砖块数并且存入d,再计算下一行并且累加到d上
3
计算整个圆的砖块数
总量sum等于d的四倍
三、编写程序
r=32
0.5
d=0
sum=0
for
i
in
range(1,int(r)+1,1):
d=d+int((r
2-i
2)
0.5)
sum=d
4
print(sum)
解释器界面:
实战演练
实战演练
①
②
1、分析已知已知条件和求解目标
2、抽象得出数学模型
3、代入数值求解
解析算法
1、分析问题
2、抽象建模
3、基于解析算法设计程序
4、编程调试
基于解析算法的问题解决
小结
小结
作业
作业
