浙教版七上5.3 一元一次方程的解法(1) 课件(共23张PPT)
文档属性
| 名称 | 浙教版七上5.3 一元一次方程的解法(1) 课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 781.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 11:07:44 | ||
图片预览






文档简介
(共23张PPT)
浙教版数学七年级(上)
5.3
一元一次方程的解法(1)
性质1、等式两边同时加上(或减去)同一个代数式,
所得结果仍是等式。
若
x=y,
那么x+a
=
y+a
性质2、等式两边同时乘以一个(或除以同一
个不为0的)数,
所得结果仍是等式。
若
x=y,
那么cx
=
cy
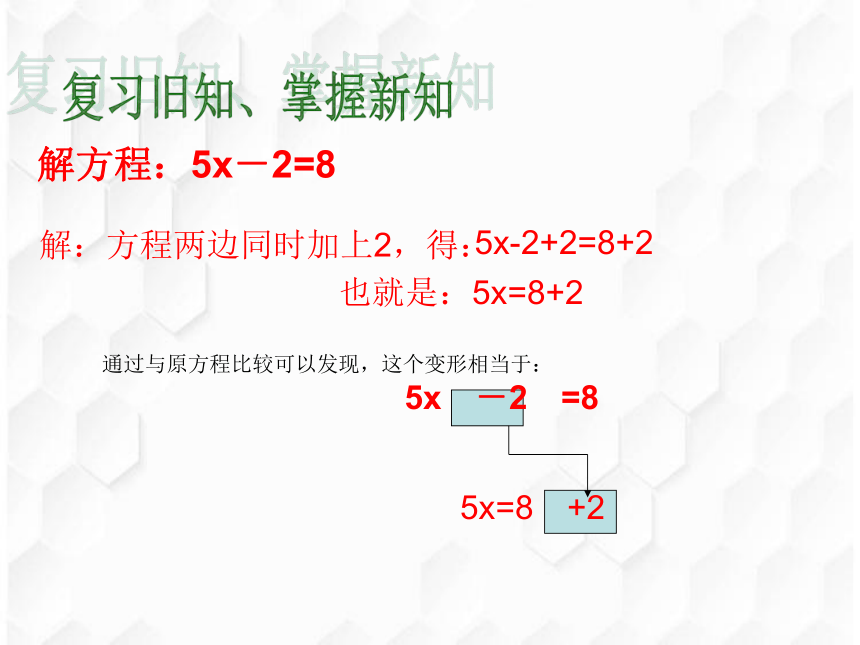
解方程:5x-2=8
解:方程两边同时加上2,得:
5x-2+2=8+2
也就是:5x=8+2
通过与原方程比较可以发现,这个变形相当于:
5x -2 =8
5x=8 +2
解方程:7x
=
6x
-
4
解:方程两边都减去
6x
,得:
7x
–
6x
=
6x
–
4
–
6x
7x
–
6x
=
–
4
通过与原方程比较可以发现,这个变形相当于:
7x
=
6x
-
4
7x
–
6x
=
–
4
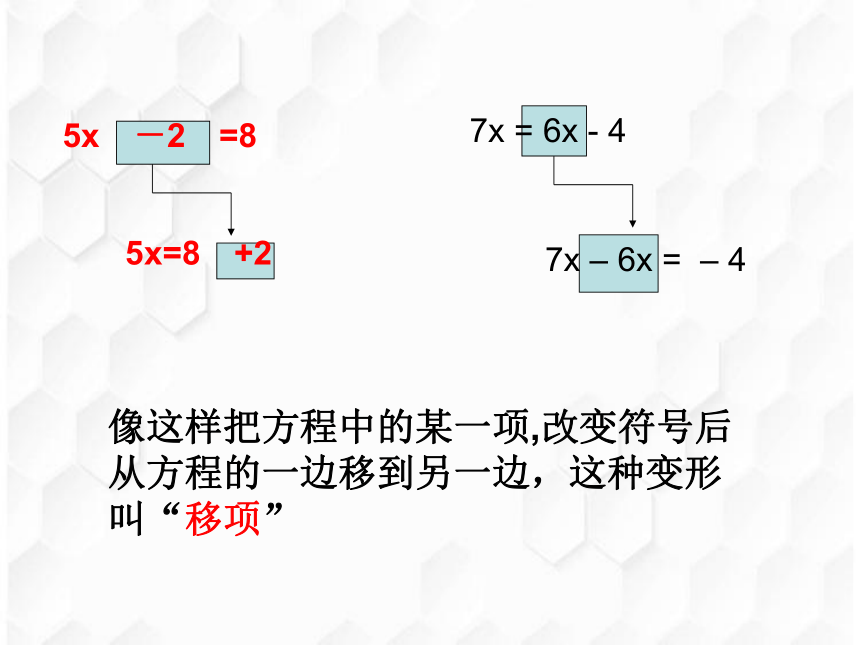
5x -2 =8
5x=8 +2
7x
=
6x
-
4
7x
–
6x
=
–
4
像这样把方程中的某一项,改变符号后从方程的一边移到另一边,这种变形叫“移项”
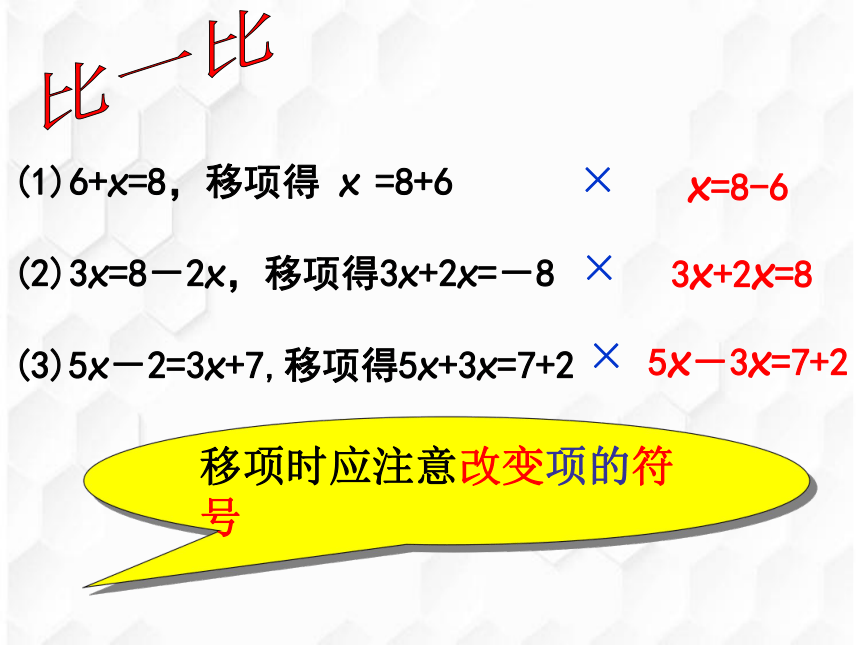
(1)6+x=8,移项得
x
=8+6
(2)3x=8-2x,移项得3x+2x=-8
(3)5x-2=3x+7,移项得5x+3x=7+2
×
x=8-6
×
3x+2x=8
×
5x-3x=7+2
移项时应注意改变项的符号
移项
合并同类项
系数化为1
求方程的解,就是将
方程变形为____的形式
x=a
结论:
(
1)2x+6=0
解:移项,得:
2x=0-6
化简,得:
2x=-6
两边同时除以2,得:
x=-3
(2)
3x+3=x+7
解:
移项,
得:3
x
–
x
=
7
-
3
化简,
得:
2x
=
4
两边同时除以2,得:
x
=
2
例1、解方程:
(1)
2x+6=0
(2)3x+3=2x+7
1.移项:把含未知数的项移到方程的一边,把常数项移到方程的另一边。
2.合并同类项。
3.把未知数的系数化为1
通过以上解方程你能总结出它的解题步骤吗?
归纳
解方程:4(x+0.5)+x=17.
此方程与上面所学方程有何差异?
须先去括号
去括号有什么注意事项呢?
解方程:
x-6(2x-1)=4.
此方程又该如何解呢?
解:去括号,
得
x-12x+6=4.
移项,
得
x–12x=4-6.
合并同类项,
得
-11x=-2.
方程两边同除以-11,得
x=2/11.
将含未知数的项放在方程的一边,常数项放在方程的另一边,对方程进行移项变形。
(2)
5x=3x-1
(1)
2x-3=6
(3)
2.4y+2=-2y
⑷
8-5x=x+2
2x
=
6
+
3
5x
-3x
=
-1
2.4y+2y
=
-2
-5x-x=2-8
抢答
2、下列变形对吗?若不对,请说明理由,并改正:
解方程
去括号,得
移项,得
合并同类项,得
两边同除以-0.2得
去括号变形错,有一项
没变号,改正如下:
去括号,得3-0.4x-2=0.2x
移项,得
-0.4x-0.2x=-3+2
合并同类项,得
-0.6x=-1
∴
3、
解下列方程,并口算检验
(3)
10x-3=7x+3;
(4)8-5x=x+2
(1)
2.4x-2=
2x;
(2)
3x+1
=
-2
⑴解:移项,得2.4x-2x=2
即0.4x=2
两边除以0.4,得
x=5
(2)解:移项,得3x=-2-1
即
3x=-3
两边除以3,得
x=-1
(3)解:移项,得10x-7x=3+3
即
3x=6
两边除以3,得
x=2
(4)解:移项,得-5x-x=2-8
即
-6x=-6
两边除以-6,得
x=1
问题:
小平的爸爸新买了一部手机,他从电
信公司了解到现在有两种计费方式:
全球通
神州行
月租费
50元/月
0
本地通话费
0.40元/分
0.60元/分
他认为选哪一种方式优越呢!你能帮助他作个选择吗?
你会吗???
(1)一个月内通话200分和300分,按两种计费方式各需交多少元?
通话200分,按两种计费方式各需交费:
50+0.40×200=130(元)
0.60×200=120(元)
(2)对于某个通话时间,两种计费方式的收费会一样吗?
设累计通话x分,则用“全球通”要收费(50+0.4t)元,用“神州行”要收费0.6t元,如果两种计费方式的收费一样,则
0.6t=50+0.4t(t=250分)
此时两种计费方式收费都为150元。
(3)怎样选择计费方式更省钱?
如果一个月内累计通话时间不足250分,那么选择“神州行”收费少;如果一个月内累计通话时间超过250分,那么选择“全球通”收费少。
(1)
2-3(x-5)=2x;
(3)2(x-1)-
(
x
-3)
=
2(1.5x-2.5)
(2)
4(4+y)=3(y-3)
2、已知:x=2是关于x的方程
(1-
2ax)=x+a
的解,求a的值
解下列方程:
(4)
5x+2(1-3x)=3(
2
-
x)
练习1
浙教版数学七年级(上)
5.3
一元一次方程的解法(1)
性质1、等式两边同时加上(或减去)同一个代数式,
所得结果仍是等式。
若
x=y,
那么x+a
=
y+a
性质2、等式两边同时乘以一个(或除以同一
个不为0的)数,
所得结果仍是等式。
若
x=y,
那么cx
=
cy
解方程:5x-2=8
解:方程两边同时加上2,得:
5x-2+2=8+2
也就是:5x=8+2
通过与原方程比较可以发现,这个变形相当于:
5x -2 =8
5x=8 +2
解方程:7x
=
6x
-
4
解:方程两边都减去
6x
,得:
7x
–
6x
=
6x
–
4
–
6x
7x
–
6x
=
–
4
通过与原方程比较可以发现,这个变形相当于:
7x
=
6x
-
4
7x
–
6x
=
–
4
5x -2 =8
5x=8 +2
7x
=
6x
-
4
7x
–
6x
=
–
4
像这样把方程中的某一项,改变符号后从方程的一边移到另一边,这种变形叫“移项”
(1)6+x=8,移项得
x
=8+6
(2)3x=8-2x,移项得3x+2x=-8
(3)5x-2=3x+7,移项得5x+3x=7+2
×
x=8-6
×
3x+2x=8
×
5x-3x=7+2
移项时应注意改变项的符号
移项
合并同类项
系数化为1
求方程的解,就是将
方程变形为____的形式
x=a
结论:
(
1)2x+6=0
解:移项,得:
2x=0-6
化简,得:
2x=-6
两边同时除以2,得:
x=-3
(2)
3x+3=x+7
解:
移项,
得:3
x
–
x
=
7
-
3
化简,
得:
2x
=
4
两边同时除以2,得:
x
=
2
例1、解方程:
(1)
2x+6=0
(2)3x+3=2x+7
1.移项:把含未知数的项移到方程的一边,把常数项移到方程的另一边。
2.合并同类项。
3.把未知数的系数化为1
通过以上解方程你能总结出它的解题步骤吗?
归纳
解方程:4(x+0.5)+x=17.
此方程与上面所学方程有何差异?
须先去括号
去括号有什么注意事项呢?
解方程:
x-6(2x-1)=4.
此方程又该如何解呢?
解:去括号,
得
x-12x+6=4.
移项,
得
x–12x=4-6.
合并同类项,
得
-11x=-2.
方程两边同除以-11,得
x=2/11.
将含未知数的项放在方程的一边,常数项放在方程的另一边,对方程进行移项变形。
(2)
5x=3x-1
(1)
2x-3=6
(3)
2.4y+2=-2y
⑷
8-5x=x+2
2x
=
6
+
3
5x
-3x
=
-1
2.4y+2y
=
-2
-5x-x=2-8
抢答
2、下列变形对吗?若不对,请说明理由,并改正:
解方程
去括号,得
移项,得
合并同类项,得
两边同除以-0.2得
去括号变形错,有一项
没变号,改正如下:
去括号,得3-0.4x-2=0.2x
移项,得
-0.4x-0.2x=-3+2
合并同类项,得
-0.6x=-1
∴
3、
解下列方程,并口算检验
(3)
10x-3=7x+3;
(4)8-5x=x+2
(1)
2.4x-2=
2x;
(2)
3x+1
=
-2
⑴解:移项,得2.4x-2x=2
即0.4x=2
两边除以0.4,得
x=5
(2)解:移项,得3x=-2-1
即
3x=-3
两边除以3,得
x=-1
(3)解:移项,得10x-7x=3+3
即
3x=6
两边除以3,得
x=2
(4)解:移项,得-5x-x=2-8
即
-6x=-6
两边除以-6,得
x=1
问题:
小平的爸爸新买了一部手机,他从电
信公司了解到现在有两种计费方式:
全球通
神州行
月租费
50元/月
0
本地通话费
0.40元/分
0.60元/分
他认为选哪一种方式优越呢!你能帮助他作个选择吗?
你会吗???
(1)一个月内通话200分和300分,按两种计费方式各需交多少元?
通话200分,按两种计费方式各需交费:
50+0.40×200=130(元)
0.60×200=120(元)
(2)对于某个通话时间,两种计费方式的收费会一样吗?
设累计通话x分,则用“全球通”要收费(50+0.4t)元,用“神州行”要收费0.6t元,如果两种计费方式的收费一样,则
0.6t=50+0.4t(t=250分)
此时两种计费方式收费都为150元。
(3)怎样选择计费方式更省钱?
如果一个月内累计通话时间不足250分,那么选择“神州行”收费少;如果一个月内累计通话时间超过250分,那么选择“全球通”收费少。
(1)
2-3(x-5)=2x;
(3)2(x-1)-
(
x
-3)
=
2(1.5x-2.5)
(2)
4(4+y)=3(y-3)
2、已知:x=2是关于x的方程
(1-
2ax)=x+a
的解,求a的值
解下列方程:
(4)
5x+2(1-3x)=3(
2
-
x)
练习1
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
