浙教版八上1.5.2 ASA及AAS的判定 教案
文档属性
| 名称 | 浙教版八上1.5.2 ASA及AAS的判定 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 14:25:58 | ||
图片预览


文档简介
三角形全等的条件
【学习目标】:
1.通过探究两个三角形具备三个条件两边及其夹角对应相等,得到
三角形全等的另一判定方法。
2.能初步应用“边角边”条件判定两个三角形全等.
【学习重难点】:
1.重点:SAS结论及其运用.
2.难点:领会SAS结论.
教学过程
导入
回顾与思考
有三边对应相等的两个三角形全等(简写成“边边边”或“SSS”)
新课讲授
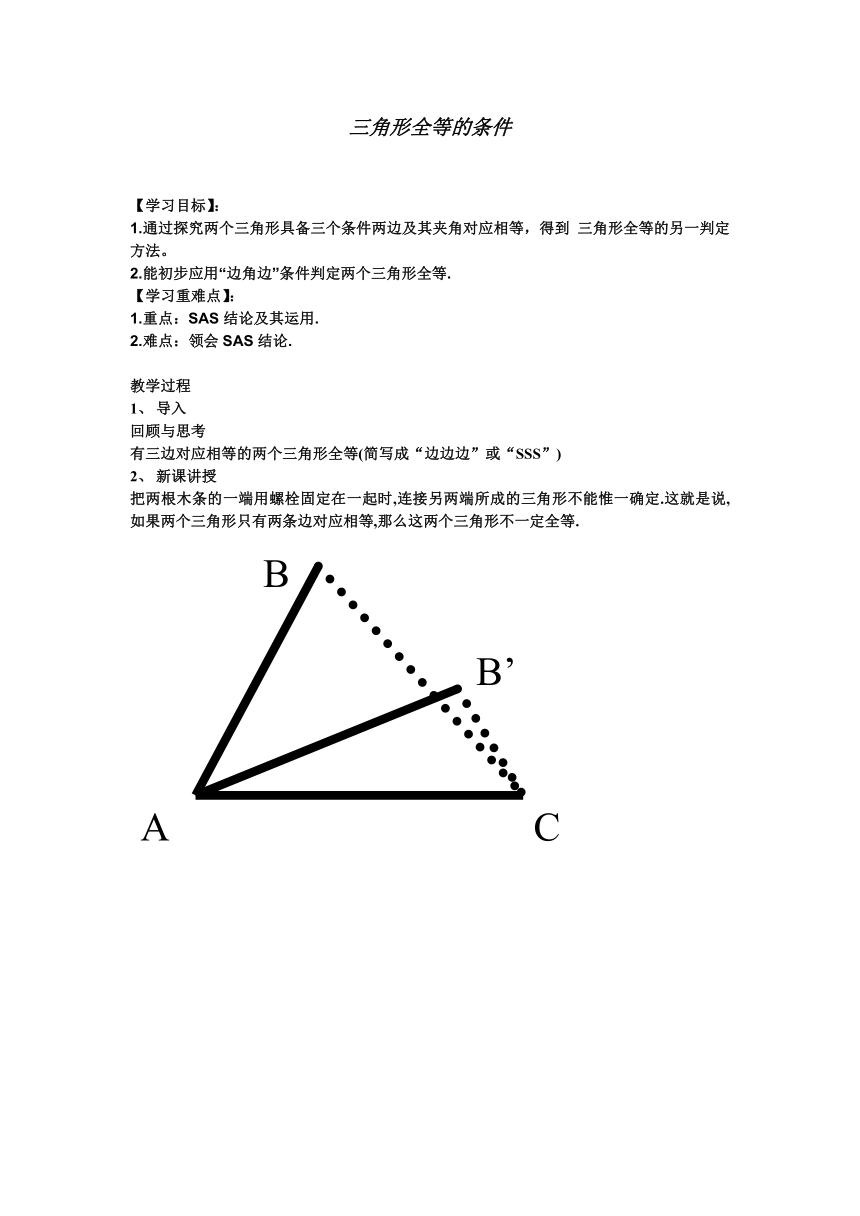
把两根木条的一端用螺栓固定在一起时,连接另两端所成的三角形不能惟一确定.这就是说,如果两个三角形只有两条边对应相等,那么这两个三角形不一定全等.
用量角器和刻度尺画△ABC,使AB=4cm,BC=6cm,∠ABC=600。
画法:
1、∠MBN=60°;
2、在射线BM上截取AB=4cm;
3、在射线BN上截取BC=6cm;
4、连接AC
∴△ABC就是所求的三角形
想一想:
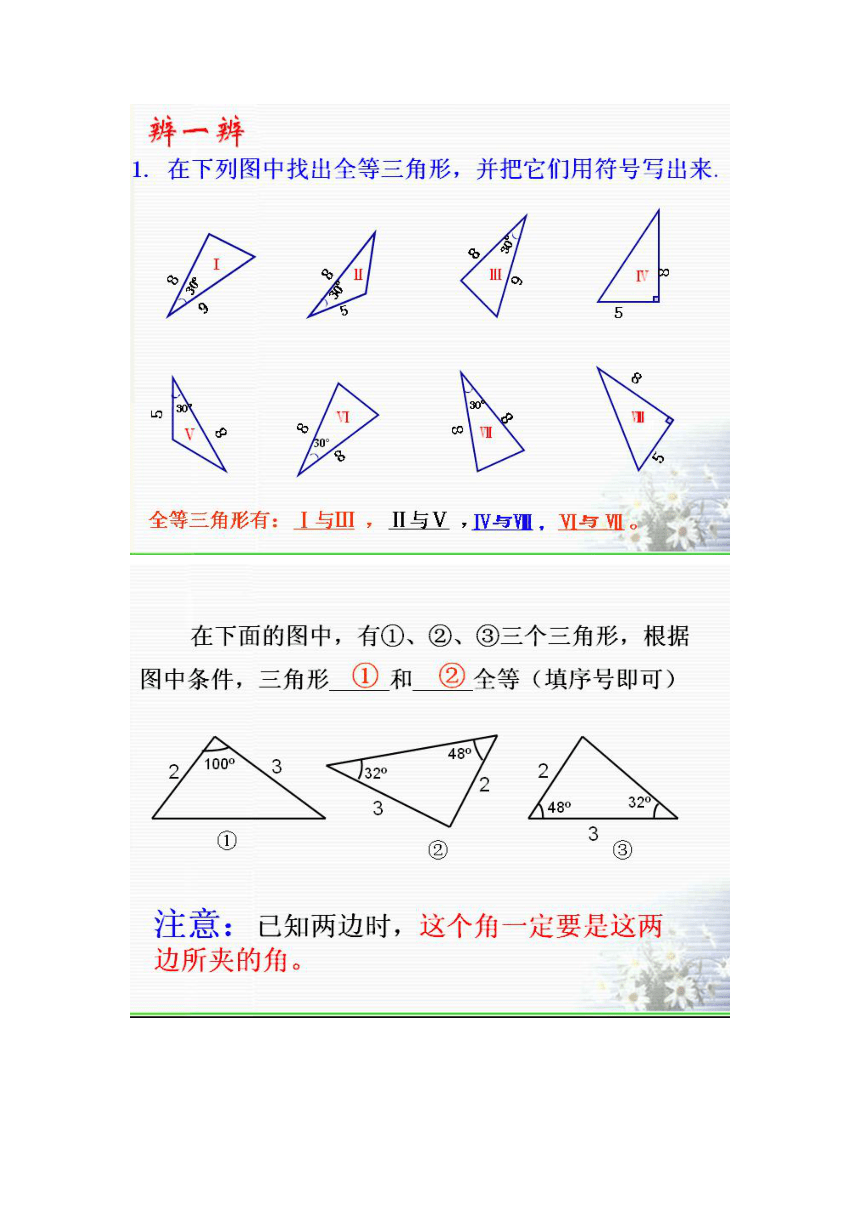
有两边和一个角对应相等的两个三角形全等吗?
把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?
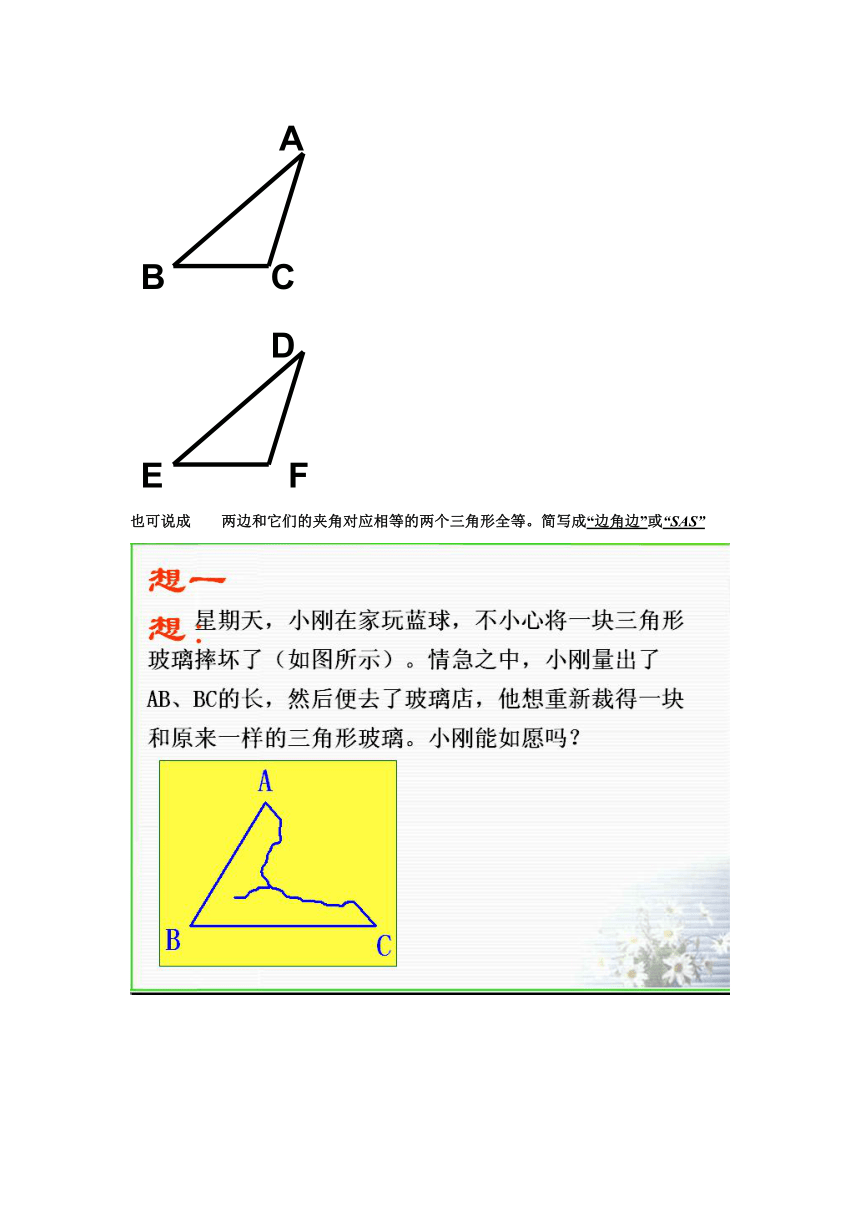
三角形全等判定方法2
有一个角和夹这个角的两边对应相等的两个三角形全等。
用数学语言表达为:
在△ABC与△DEF中
AB=DE
∠B=∠E
BC=EF
∴△ABC≌△DEF(SAS)
也可说成
两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”
四、课堂小结
五、课堂反思
通过本节课的学习,我的收获和困惑是
A
B’
C
B
A
B
C
D
E
F
【学习目标】:
1.通过探究两个三角形具备三个条件两边及其夹角对应相等,得到
三角形全等的另一判定方法。
2.能初步应用“边角边”条件判定两个三角形全等.
【学习重难点】:
1.重点:SAS结论及其运用.
2.难点:领会SAS结论.
教学过程
导入
回顾与思考
有三边对应相等的两个三角形全等(简写成“边边边”或“SSS”)
新课讲授
把两根木条的一端用螺栓固定在一起时,连接另两端所成的三角形不能惟一确定.这就是说,如果两个三角形只有两条边对应相等,那么这两个三角形不一定全等.
用量角器和刻度尺画△ABC,使AB=4cm,BC=6cm,∠ABC=600。
画法:
1、∠MBN=60°;
2、在射线BM上截取AB=4cm;
3、在射线BN上截取BC=6cm;
4、连接AC
∴△ABC就是所求的三角形
想一想:
有两边和一个角对应相等的两个三角形全等吗?
把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?
三角形全等判定方法2
有一个角和夹这个角的两边对应相等的两个三角形全等。
用数学语言表达为:
在△ABC与△DEF中
AB=DE
∠B=∠E
BC=EF
∴△ABC≌△DEF(SAS)
也可说成
两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”
四、课堂小结
五、课堂反思
通过本节课的学习,我的收获和困惑是
A
B’
C
B
A
B
C
D
E
F
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
