浙教版八上4.3.2 坐标平面内图形的轴对称和平移 课件(12张)
文档属性
| 名称 | 浙教版八上4.3.2 坐标平面内图形的轴对称和平移 课件(12张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 267.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 00:00:00 | ||
图片预览





文档简介
(共12张PPT)
4.3
坐标平面内
图形的轴对称和平(2)
x
y
O
1
2
3
4
2
4
1
3
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
5
-6
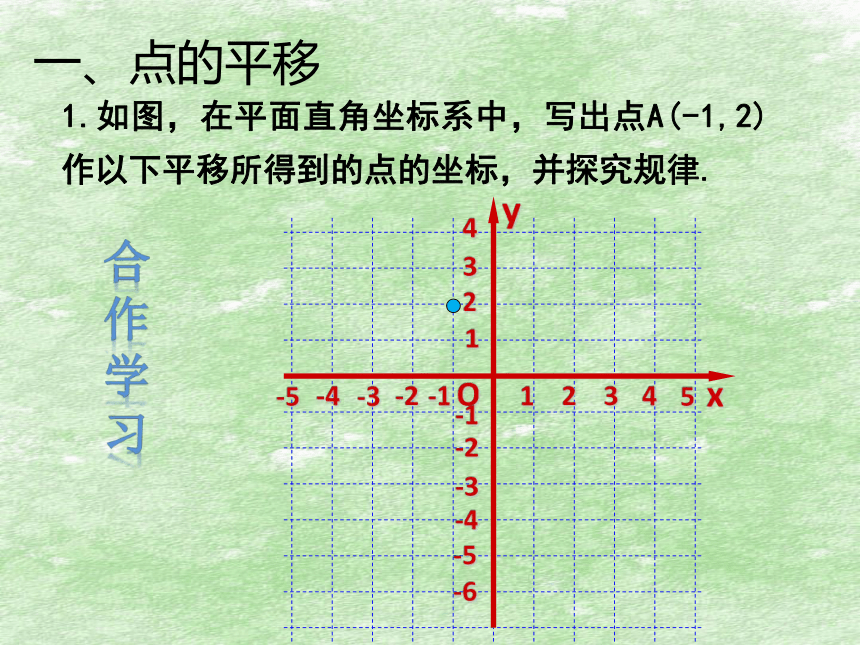
一、点的平移
合作学习
1.如图,在平面直角坐标系中,写出点A(-1,2)作以下平移所得到的点的坐标,并探究规律.
平移
像的坐标
横坐标变化
纵坐标变化
A(-1,2)
向右平移5个单位
向左平移3个单位
向上平移2个单位
向下平移7个单位
(1)填表
(2)你能总结出什么规律?
x
y
O
1
2
3
4
2
4
1
3
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
5
-6
A4(-1,-5)
A1(4,2)
加5
不变
减3
加2
减7
不变
不变
不变
A2(-4,2)
A3(-1,4)
横移横变,纵移纵变
正加负减
形
数
(1)已知点A的坐标为(-2,-3),分别求点经下列平移变换后所得的像的坐标.
①向上平移3个单位
③向左平移2个单位
(-2,
0)
(-2,-6)
(-4,-3)
(
2,-3)
⑤先向右平移3个单位,再向下平移3个单位
(1,
-6)
②向下平移3个单位
④向右平移4个单位
2.你学会了么?
横移横变,纵移纵变
正加负减
(2)请设计一个或一组平移,使
①点(2,5)变换成(2,-5)
②点(-3,-4)变换为(1,0)
横移横变,纵移纵变
正加负减
线段AB在直角坐标系中的位置如图所示,回答问题:
二、线段平移
P1
P2
P3
P4
P5
A
(1,-1)
B
(5,-1)
P1(2,-1)
P2(3,-1)
P3(4,-1)
P4(2.5,-1)
P5(3.5,-1)
A
B
1
2
3
4
0
1
2
4
3
5
-1
-1
-2
x
y
...
仔细观察这些点的横坐标和纵坐标,你有什么发现?
1
2
3
4
0
1
2
4
3
5
-1
-1
-2
A
B
x
y
(x,-1)
(1≤x≤5)
1.怎样表示线段AB上任意一点的坐标?
1
2
3
4
0
1
2
4
3
5
-1
-1
-2
x
y
2.怎样表示线段CD上任意一点的坐标?
(2,y)
(-1≤y≤3)
C
D
3.把线段CD向左平移3个单位得到线段C'D',如何表示线段C'D'上任意一点的坐标?
(-1,y)
(-1≤y
≤3)
A
B
1
2
3
4
0
1
2
4
3
5
-1
-1
-2
x
y
4.线段AB可以通过怎样的平移得到线段EF?
可以通过一次平移得到么?
E
F
沿AE方向平移
个单位长度
1.如图,你能通过两次平移把△ABC的顶点A变换为点O吗?写出你的平移方法,并求出△OB
'
C
'的顶点坐标.
x
y
0
1
2
3
1
2
3
B
C
A
O
D
三、图形平移
解:
5
4
-2
-3
-2
-1
-3
-1
O(0,0)
发生了什么变换?
A(3,5)
B(0,3)
C(2,0)
B
'(-3,-2)
C'(-1,-5)
2.你能通过一次平移实现上述过程吗?请求出平移的方向和距离.
x
y
0
1
2
3
1
2
3
B
C
A
B'
C'
O
D
连接AO,
过点A作AD⊥x
轴,由勾股定理可得
解:
三、图形平移
∴
△ABC沿着AO方向平移了
个单位长度.
5
4
-2
-3
-2
-1
-3
-1
四、课堂小结
数形结合
点的平移
线的平移
面的平移
4.3
坐标平面内
图形的轴对称和平(2)
x
y
O
1
2
3
4
2
4
1
3
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
5
-6
一、点的平移
合作学习
1.如图,在平面直角坐标系中,写出点A(-1,2)作以下平移所得到的点的坐标,并探究规律.
平移
像的坐标
横坐标变化
纵坐标变化
A(-1,2)
向右平移5个单位
向左平移3个单位
向上平移2个单位
向下平移7个单位
(1)填表
(2)你能总结出什么规律?
x
y
O
1
2
3
4
2
4
1
3
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
5
-6
A4(-1,-5)
A1(4,2)
加5
不变
减3
加2
减7
不变
不变
不变
A2(-4,2)
A3(-1,4)
横移横变,纵移纵变
正加负减
形
数
(1)已知点A的坐标为(-2,-3),分别求点经下列平移变换后所得的像的坐标.
①向上平移3个单位
③向左平移2个单位
(-2,
0)
(-2,-6)
(-4,-3)
(
2,-3)
⑤先向右平移3个单位,再向下平移3个单位
(1,
-6)
②向下平移3个单位
④向右平移4个单位
2.你学会了么?
横移横变,纵移纵变
正加负减
(2)请设计一个或一组平移,使
①点(2,5)变换成(2,-5)
②点(-3,-4)变换为(1,0)
横移横变,纵移纵变
正加负减
线段AB在直角坐标系中的位置如图所示,回答问题:
二、线段平移
P1
P2
P3
P4
P5
A
(1,-1)
B
(5,-1)
P1(2,-1)
P2(3,-1)
P3(4,-1)
P4(2.5,-1)
P5(3.5,-1)
A
B
1
2
3
4
0
1
2
4
3
5
-1
-1
-2
x
y
...
仔细观察这些点的横坐标和纵坐标,你有什么发现?
1
2
3
4
0
1
2
4
3
5
-1
-1
-2
A
B
x
y
(x,-1)
(1≤x≤5)
1.怎样表示线段AB上任意一点的坐标?
1
2
3
4
0
1
2
4
3
5
-1
-1
-2
x
y
2.怎样表示线段CD上任意一点的坐标?
(2,y)
(-1≤y≤3)
C
D
3.把线段CD向左平移3个单位得到线段C'D',如何表示线段C'D'上任意一点的坐标?
(-1,y)
(-1≤y
≤3)
A
B
1
2
3
4
0
1
2
4
3
5
-1
-1
-2
x
y
4.线段AB可以通过怎样的平移得到线段EF?
可以通过一次平移得到么?
E
F
沿AE方向平移
个单位长度
1.如图,你能通过两次平移把△ABC的顶点A变换为点O吗?写出你的平移方法,并求出△OB
'
C
'的顶点坐标.
x
y
0
1
2
3
1
2
3
B
C
A
O
D
三、图形平移
解:
5
4
-2
-3
-2
-1
-3
-1
O(0,0)
发生了什么变换?
A(3,5)
B(0,3)
C(2,0)
B
'(-3,-2)
C'(-1,-5)
2.你能通过一次平移实现上述过程吗?请求出平移的方向和距离.
x
y
0
1
2
3
1
2
3
B
C
A
B'
C'
O
D
连接AO,
过点A作AD⊥x
轴,由勾股定理可得
解:
三、图形平移
∴
△ABC沿着AO方向平移了
个单位长度.
5
4
-2
-3
-2
-1
-3
-1
四、课堂小结
数形结合
点的平移
线的平移
面的平移
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
