浙教版八上4.3.1 坐标平面内图形的轴对称和平移 课件(11张)
文档属性
| 名称 | 浙教版八上4.3.1 坐标平面内图形的轴对称和平移 课件(11张) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 16:21:28 | ||
图片预览


文档简介
(共11张PPT)
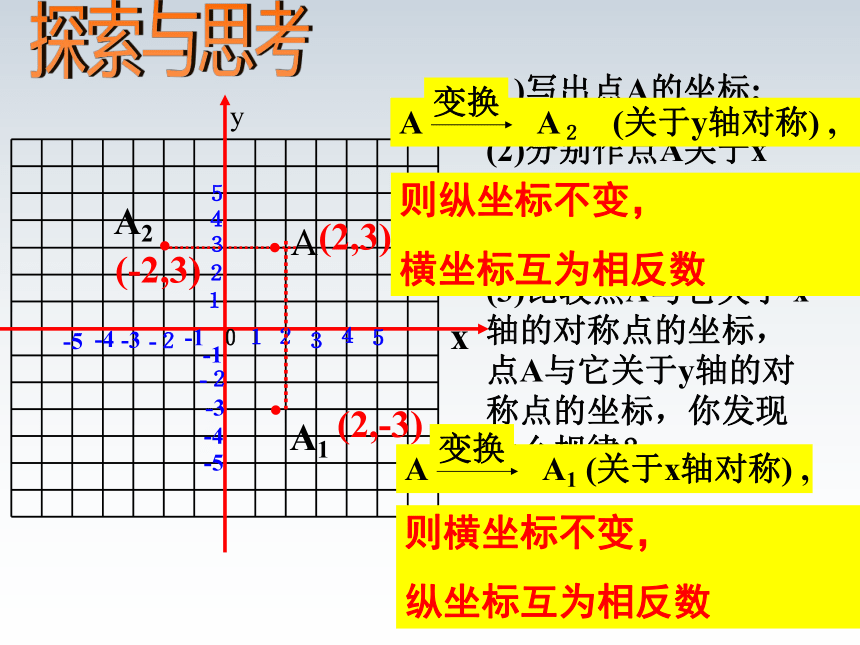
(1)写出点A的坐标;
(2)分别作点A关于x轴,y轴的对称点,并写出它们的坐标;
(3)比较点A与它关于
x轴的对称点的坐标,点A与它关于y轴的对称点的坐标,你发现什么规律?
0
2
1
-3
5
5
4
3
4
3
2
1
-2
-1
-5
-1
-4
-3
-2
-4
-5
?
A
(2,3)
?
?
A1
(2,-3)
A2
(-2,3)
则横坐标不变,
纵坐标互为相反数
则纵坐标不变,
横坐标互为相反数
x
y
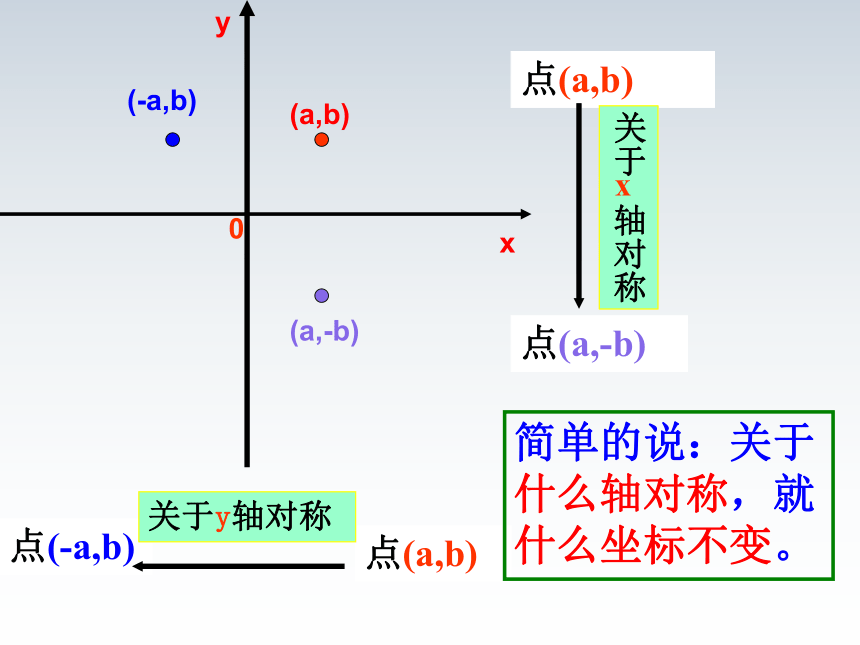
(a,b)
x
y
点(a,b)
0
(-a,b)
(a,-b)
点(a,-b)
点(-a,b)
关于
轴对称
x
点(a,b)
关于y轴对称
简单的说:关于什么轴对称,就什么坐标不变。
比一比:看谁反应快
已知点A(-1,2),关于x轴的对称点是________
(-1,-2)
已知点B(1,-
)
关于y轴的对称点是____
(-1,
)
已知点C(-2,3)关于y轴的对称点是_____
(2,3)
已知点D(0,1.5)关于x轴的对称点是_________
(0,-1.5)
已知点E(8,0),关于y轴的对称点是
____
(-8,0)
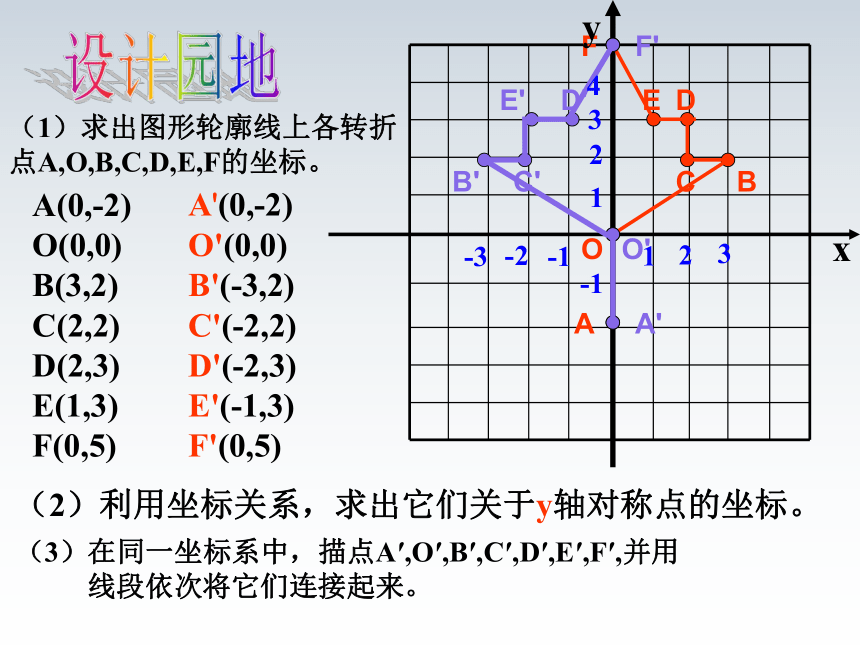
(2)利用坐标关系,求出它们关于y轴对称点的坐标。
A
O
C
B
D
E
F
(1)求出图形轮廓线上各转折点A,O,B,C,D,E,F的坐标。
A(0,-2)
O(0,0)
B(3,2)
C(2,2)
D(2,3)
E(1,3)
F(0,5)
A'(0,-2)
O'(0,0)
B'(-3,2)
C'(-2,2)
D'(-2,3)
E'(-1,3)
F'(0,5)
(3)在同一坐标系中,描点A′,O′,B′,C′,D′,E′,F′,并用
线段依次将它们连接起来。
A'
O'
B'
C'
E'
D'
F'
x
y
-2
-1
3
2
1
-3
3
2
1
-1
4
A
O
C
B
D
E
F
A'
O'
B'
C'
E'
D'
F'
把一个轴对称图形画在直角坐标系中,怎样画最简便呢?
1、使对称轴与坐标轴重合
2、画出一侧的关键点,并求坐标
3、利用坐标关系,求另一侧关键点坐标
4、描点、连线
x
y
(1)求出?ABO各顶点的坐标,以及它们关于y轴的对称点的坐标并描点、最后连线
A
B
(1,2)
(2,1)
(-2,1)
(-1,2)
(0,0)
o
x
y
如何画出已知?ABO关于y轴对称的图形??
(2)将?ABO以x轴为对称轴作一次轴对称变换,然后将所得的像连同原图形,以y轴为对称轴再作一次轴对称变换,分别作出经两次变换后所得的像。
A
B
(1,-2)
(2,1)
(1,2)
(-1,-2)
(0,0)
(-1,2)
(-2,1)
(-2,-1)
(2,-1)
O
x
y
2
3
1
1
1、按你自己所认为合适的比例,建立直角坐标系。
2、在直角坐标系中选取适当的位置,作出这个主视图,标明比例,并求出轮廓线各个转折点的坐标。
这是一个零件的主视图
500
100
400
100
150
单位:mm
你能用图形变换的观点加以绘制吗?
将?ABO各顶点的横坐标乘以-1,得到的图形与原图形相比有什么变化?
A
B
(2,3)
(4,0)
(0,0)
O
这一过程,可以看成一个什么变换?
x
y
2
3
1
1
2
-2
-2
-3
纵
横、纵
小结
1、关于坐标轴对称的两个点坐标关系:
A
A1
(关于x轴对称)
,
变换
则横坐标不变,纵坐标互为相反数
A
A2
(关于y轴对称)
,
变换
则纵坐标不变,横坐标互为相反数
即:关于什么轴对称,就什么坐标不变。
2、利用关于坐标轴对称的两个点的坐标关系,求作轴对称图形
(1)使对称轴与坐标轴重合
(2)画出一侧的关键点,并求坐标
(3)利用坐标关系,求另一侧关键点坐标
(4)描点、连线
(1)写出点A的坐标;
(2)分别作点A关于x轴,y轴的对称点,并写出它们的坐标;
(3)比较点A与它关于
x轴的对称点的坐标,点A与它关于y轴的对称点的坐标,你发现什么规律?
0
2
1
-3
5
5
4
3
4
3
2
1
-2
-1
-5
-1
-4
-3
-2
-4
-5
?
A
(2,3)
?
?
A1
(2,-3)
A2
(-2,3)
则横坐标不变,
纵坐标互为相反数
则纵坐标不变,
横坐标互为相反数
x
y
(a,b)
x
y
点(a,b)
0
(-a,b)
(a,-b)
点(a,-b)
点(-a,b)
关于
轴对称
x
点(a,b)
关于y轴对称
简单的说:关于什么轴对称,就什么坐标不变。
比一比:看谁反应快
已知点A(-1,2),关于x轴的对称点是________
(-1,-2)
已知点B(1,-
)
关于y轴的对称点是____
(-1,
)
已知点C(-2,3)关于y轴的对称点是_____
(2,3)
已知点D(0,1.5)关于x轴的对称点是_________
(0,-1.5)
已知点E(8,0),关于y轴的对称点是
____
(-8,0)
(2)利用坐标关系,求出它们关于y轴对称点的坐标。
A
O
C
B
D
E
F
(1)求出图形轮廓线上各转折点A,O,B,C,D,E,F的坐标。
A(0,-2)
O(0,0)
B(3,2)
C(2,2)
D(2,3)
E(1,3)
F(0,5)
A'(0,-2)
O'(0,0)
B'(-3,2)
C'(-2,2)
D'(-2,3)
E'(-1,3)
F'(0,5)
(3)在同一坐标系中,描点A′,O′,B′,C′,D′,E′,F′,并用
线段依次将它们连接起来。
A'
O'
B'
C'
E'
D'
F'
x
y
-2
-1
3
2
1
-3
3
2
1
-1
4
A
O
C
B
D
E
F
A'
O'
B'
C'
E'
D'
F'
把一个轴对称图形画在直角坐标系中,怎样画最简便呢?
1、使对称轴与坐标轴重合
2、画出一侧的关键点,并求坐标
3、利用坐标关系,求另一侧关键点坐标
4、描点、连线
x
y
(1)求出?ABO各顶点的坐标,以及它们关于y轴的对称点的坐标并描点、最后连线
A
B
(1,2)
(2,1)
(-2,1)
(-1,2)
(0,0)
o
x
y
如何画出已知?ABO关于y轴对称的图形??
(2)将?ABO以x轴为对称轴作一次轴对称变换,然后将所得的像连同原图形,以y轴为对称轴再作一次轴对称变换,分别作出经两次变换后所得的像。
A
B
(1,-2)
(2,1)
(1,2)
(-1,-2)
(0,0)
(-1,2)
(-2,1)
(-2,-1)
(2,-1)
O
x
y
2
3
1
1
1、按你自己所认为合适的比例,建立直角坐标系。
2、在直角坐标系中选取适当的位置,作出这个主视图,标明比例,并求出轮廓线各个转折点的坐标。
这是一个零件的主视图
500
100
400
100
150
单位:mm
你能用图形变换的观点加以绘制吗?
将?ABO各顶点的横坐标乘以-1,得到的图形与原图形相比有什么变化?
A
B
(2,3)
(4,0)
(0,0)
O
这一过程,可以看成一个什么变换?
x
y
2
3
1
1
2
-2
-2
-3
纵
横、纵
小结
1、关于坐标轴对称的两个点坐标关系:
A
A1
(关于x轴对称)
,
变换
则横坐标不变,纵坐标互为相反数
A
A2
(关于y轴对称)
,
变换
则纵坐标不变,横坐标互为相反数
即:关于什么轴对称,就什么坐标不变。
2、利用关于坐标轴对称的两个点的坐标关系,求作轴对称图形
(1)使对称轴与坐标轴重合
(2)画出一侧的关键点,并求坐标
(3)利用坐标关系,求另一侧关键点坐标
(4)描点、连线
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
