浙教版八上5.2.1函数 课件（17张）

(共17张PPT)
5.2
函
数（1）
浙教八年级上册数学第5章
一次函数
1.小明的哥哥是一名大学生,他利用暑假去一家公司打工，报酬16元/时计算，设小明的哥哥这个月工作的时间为
t
时，应得报酬为
m
元。
请你用
t
的代数式来表示m.
填写下表:
工作时间t(时)
1
5
10
15
20
报酬m(元)
16t
80
320
240
160
16
t
发现：当变量t取某一个值时，变量m相应有几个值？
m=16t
只有一个
请同学们认真阅读题目1
2.
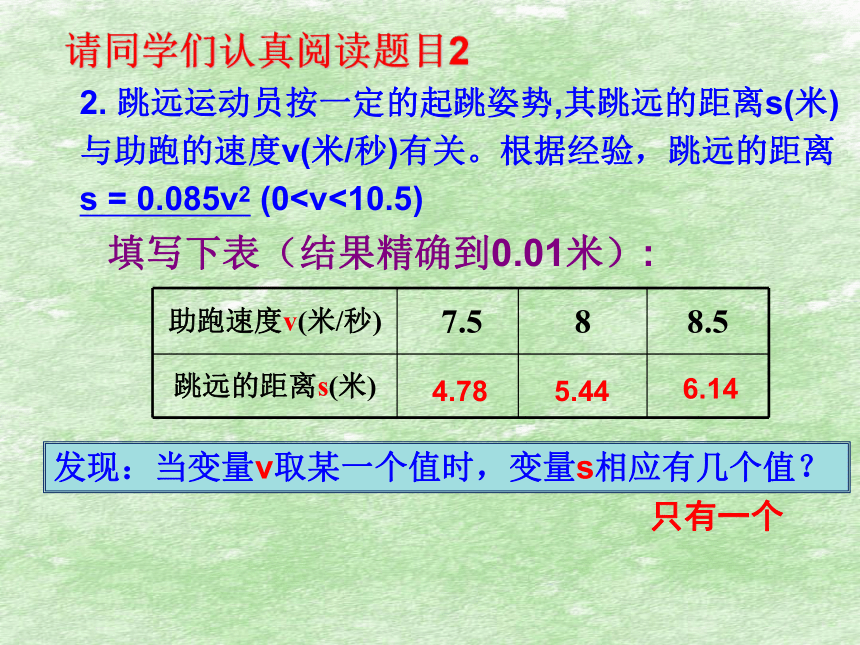
跳远运动员按一定的起跳姿势,其跳远的距离s(米)与助跑的速度v(米/秒)有关。根据经验，跳远的距离
s
=
0.085v2
(0填写下表（结果精确到0.01米）:
助跑速度v(米/秒)
7.5
8
8.5
跳远的距离s(米)
4.78
6.14
5.44
只有一个
请同学们认真阅读题目2
发现：当变量v取某一个值时，变量s相应有几个值？
只有一个
y=2x-1
请同学们认真阅读题目3
发现：变量x任意取一个值时，变量y相应有几个值？
m=16t
s
=
0.085v2
y=2x-1
函数
一般地，在某个变化过程中，设有两个变量
x、
y，如果对于
x
的每一个确定的值，
y
都有唯一确定的值，
那么就说y是x的函数，
x
叫做自变量。
我们把这样的函数关系的等式叫函数表达式，简称函数式。
问题2:
y=x2
y是x的函数吗？
x是y的函数吗？
是
不是
问题1：y=2x-1
反之x是y的函数吗？
是
函数的概念
m=16t
s
=
0.085v2
y=2x-1
根据函数的概念，知道y是x的函数.
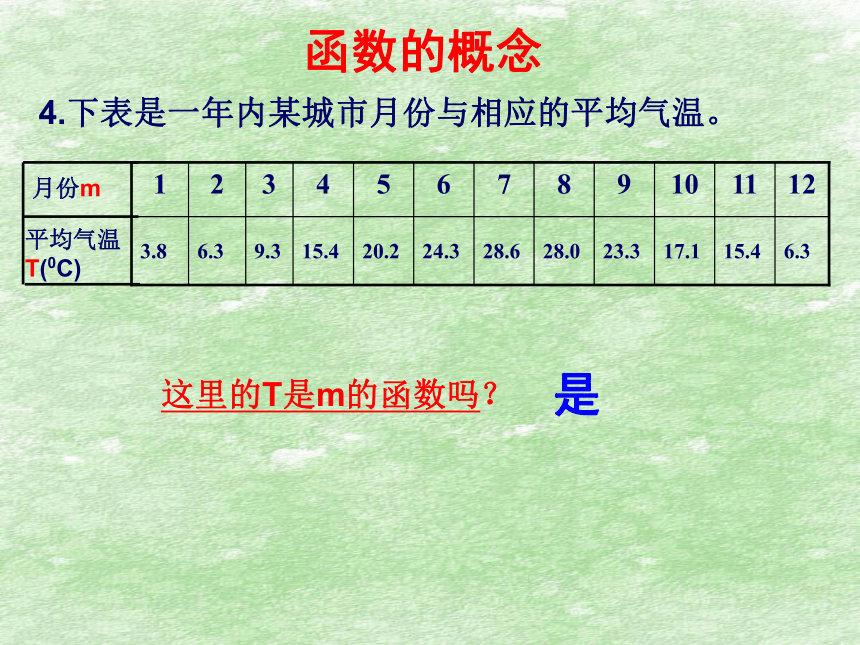
4.下表是一年内某城市月份与相应的平均气温。
6.3
15.4
17.1
23.3
28.0
28.6
24.3
20.2
15.4
9.3
6.3
3.8
12
11
10
9
8
7
6
5
4
3
2
1
月份m
平均气温T(0C)
这里的T是m的函数吗？
是
函数的概念
5.如图，图象表示骑车时热量消耗
W
(焦)与身体质量
x
(千克)之间的关系。
身体质量
x
(千克)
活动时消耗的热量W
(焦）
这里的W是x的函数吗？
是
函数的概念
以这种函数式表示函数的方法叫做解析法。
把自变量
x
的一系列值和函数
y
对应值列成一个表，这种表示函数关系的方法是列表法.
用图象来表示函数关系的方法是图象法.
什么叫函数值？
如：y=2x-1
当自变量x=-2时，
y＝
。
（1）问：y=2x-1
当自变量x=0时，
函数值是
。
这个y的值就是此时x=-2时的函数值。
（2）如下表，当m=7时，函数值T＝
。
6.3
12.2
17.1
23.3
28.0
28.6
24.3
20.2
15.4
9.3
5.1
3.8
12
11
10
9
8
7
6
5
4
3
2
1
月份m
平均气温T(0C)
活动时消耗的热量W
(焦）
身体质量
x
(千克)
（3）当
x＝40时，函数值W＝
。
-1
-5
28.6
330
练一练
你一定能行！
1.某市民用电费的价格是0.5元/千瓦时。设用电量
为x千瓦时，应付电费为y元，则y关于x的函数式
为_____________，当x=40时，函数值为________，
它的实际意义是________________________________。
20
用40千瓦时电需付电费20元
y=0.5x
2.在国内投寄平信应付邮资如下表：
3.6
2.4
1.2
邮资y（元）
40＜x≤60
20＜x≤40
0＜x≤20
信件质量x(克)
（1）求当x＝19.5
时的函数值，并说明它的实际意义。
(3)
x是y的函数吗?
答：不是，因为对于y的某一个值，x有不唯一的值。
(2)
y是x的函数吗?
当x＝19.5时，y＝1.2；
实际意义：信件质量为5g时需要邮资1.2元
答：是，因为对于x的每一个确定的值，y都有唯一确定的值。
X(m)
5
10
15
20
25
V(万m3)
3.下图是某水库的库容曲线图，其中x表示水库的平均水深(m)，V表示水库的库容（万m3）.根据图象回答下面的问题：
（1）这个函数反映了哪两个变量之间的关系？
（3）当平均水深取5m至25m之间的一个确定的值时，相应的库容V确定吗？
8
40
85
150
250
（2）填表：
（4）库容V可以看成平均水深x的函数吗？
（5）求当x=18时的函数值，并说明它的实际意义.
当x=18时，V的函数值125万m3
；
当水库的平均水深为18m时，水库的库容125万m3。
见课本第146页第5题
平均水深x（m）
平均水深x和水库的库容V
确定
可以
课堂小结
（1）函数的概念
（2）函数的三种常用表示方法
本节课你有什么收获？
（3）函数值
下列四个选项中，不是y关于x的函数的是(
)
A.
|
y
|＝x－1
B.
C.
y＝2x－7
D.
y＝x2
补充题一：
补充题二：
下图是表示某一个月的日平均温度变化的曲线，根据图象回答问题：
1.这个曲线反映了哪两个变量之间的关系？
2.日平均温度T是x的函数吗？
3.时间x是T的函数吗？
函数(概念）
函数值
函数的
表示方法
解析法（函数式）
列表法
图象法
板书设计
5.2
函数（1）