浙教版八上1.3证明2 课件(20张)
文档属性
| 名称 | 浙教版八上1.3证明2 课件(20张) |
|
|
| 格式 | ppt | ||
| 文件大小 | 791.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 16:21:28 | ||
图片预览


文档简介
(共20张PPT)
A
B
C
对于三角形,我们已经有哪些认识?
合作探索
定义
分类
内角和
…………
三角形的三个内角的和等于180°.
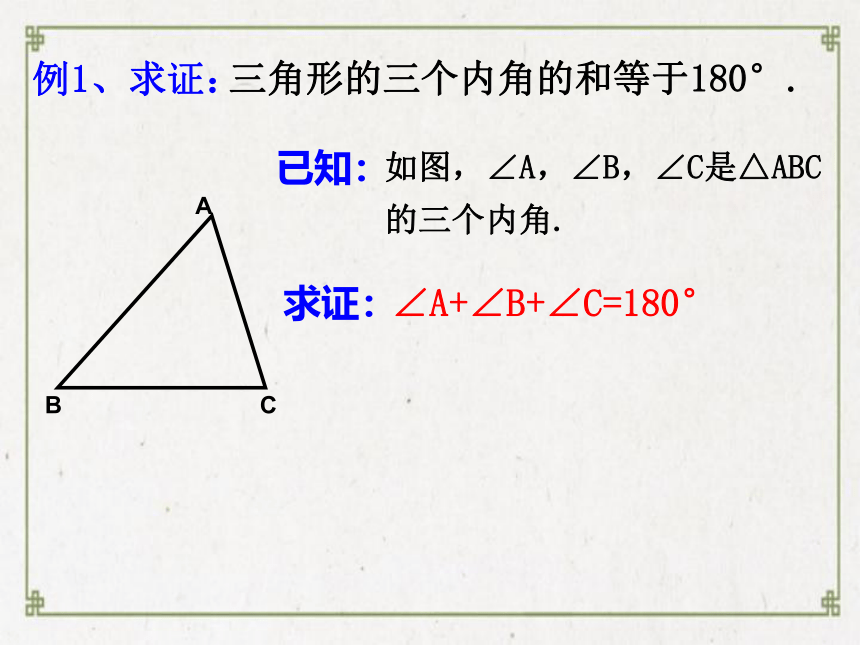
例1、求证:
A
B
C
已知:
求证:
如图,∠A,∠B,∠C是△ABC的三个内角.
∠A+∠B+∠C=180°
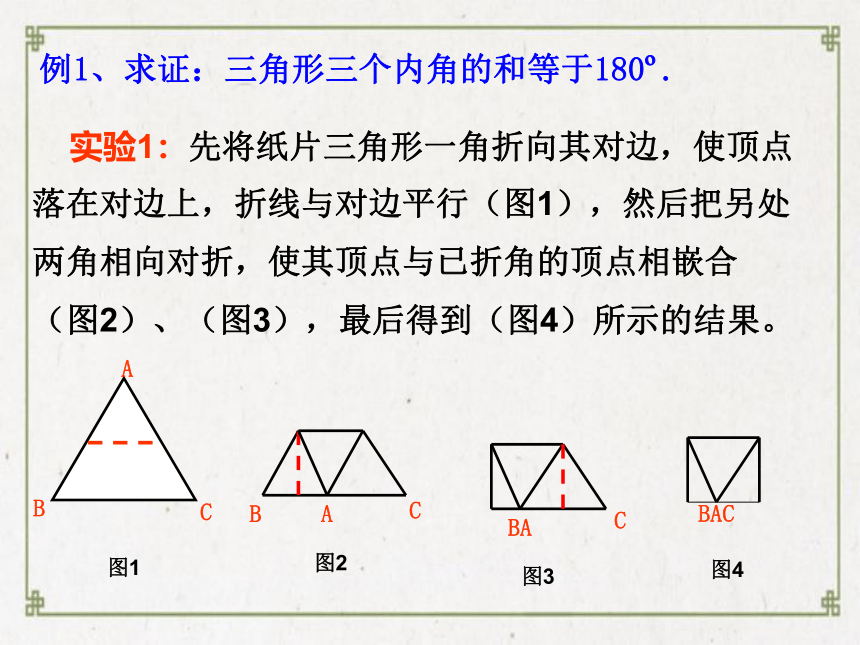
实验1:先将纸片三角形一角折向其对边,使顶点落在对边上,折线与对边平行(图1),然后把另处两角相向对折,使其顶点与已折角的顶点相嵌合(图2)、(图3),最后得到(图4)所示的结果。
A
C
B
图1
B
A
C
图2
BA
C
图3
BAC
图4
例1、求证:三角形三个内角的和等于180?.
1
1
2
A
B
D
2
3
C
1
2
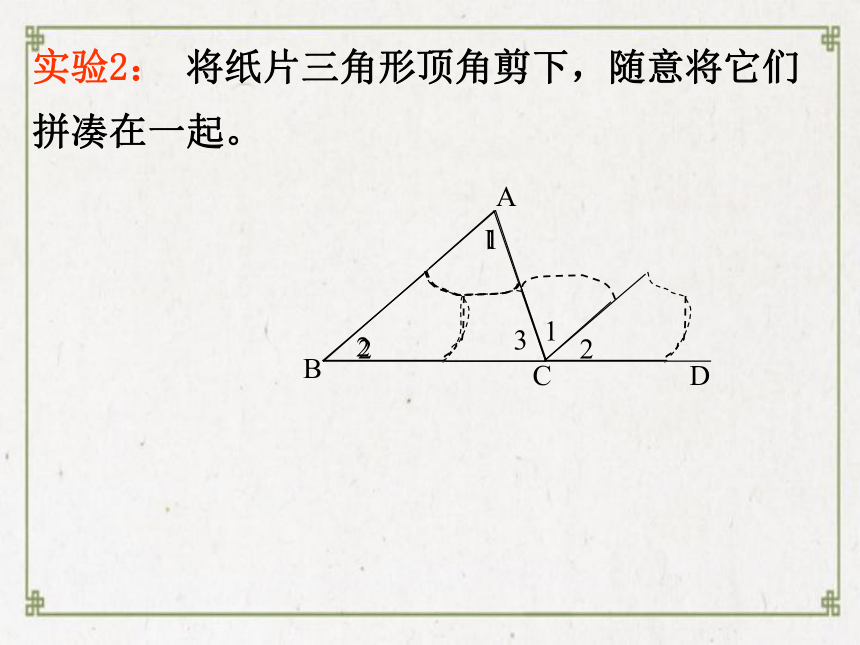
实验2:
将纸片三角形顶角剪下,随意将它们拼凑在一起。
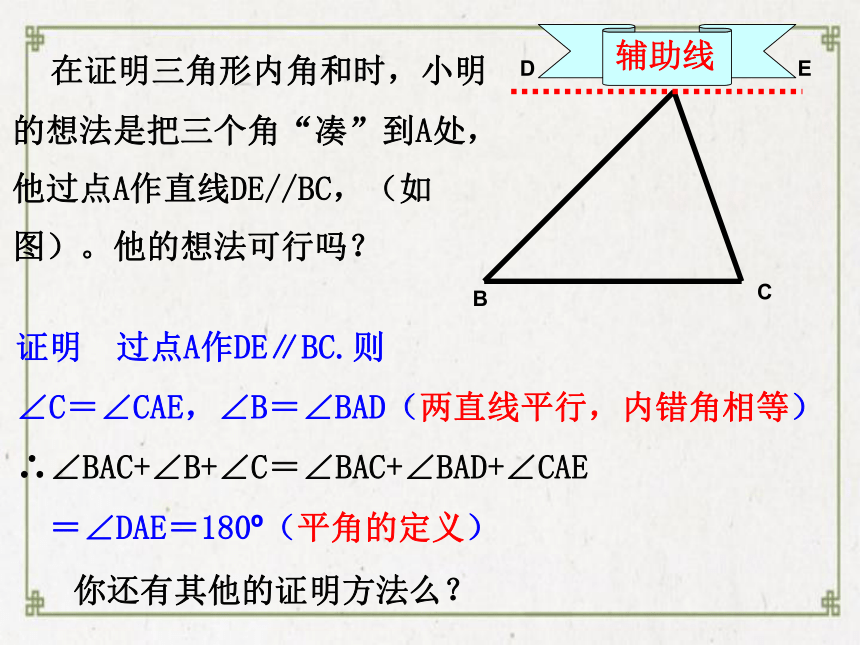
在证明三角形内角和时,小明的想法是把三个角“凑”到A处,他过点A作直线DE//BC,(如图)。他的想法可行吗?
A
B
C
E
D
证明 过点A作DE∥BC.则
∠C=∠CAE,∠B=∠BAD(两直线平行,内错角相等)
∴∠BAC+∠B+∠C=∠BAC+∠BAD+∠CAE
=∠DAE=180?(平角的定义)
你还有其他的证明方法么?
辅助线
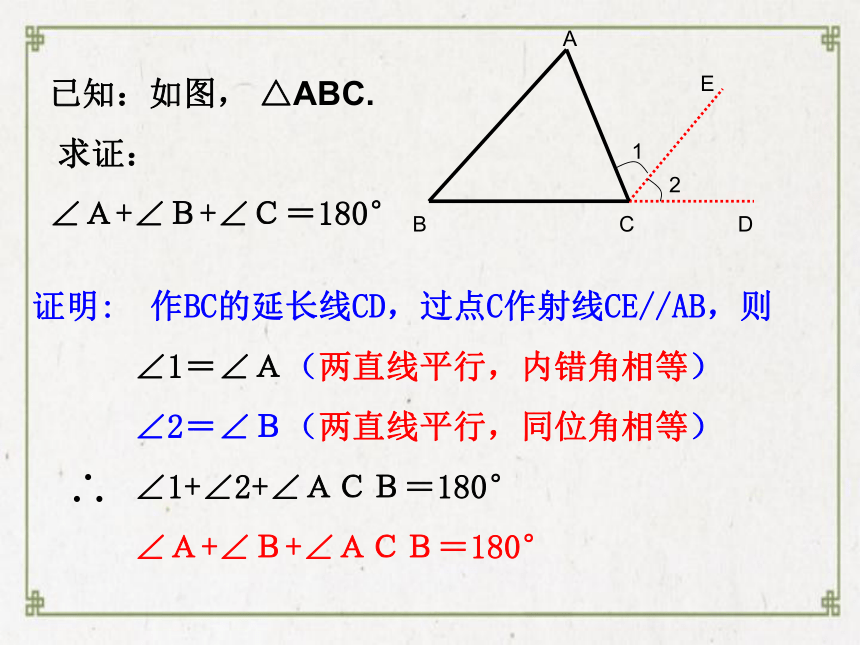
已知:如图,
△ABC.
求证:
∠A+∠B+∠C=180°
A
B
C
1
2
D
E
证明:
作BC的延长线CD,过点C作射线CE//AB,则
∠1=∠A(两直线平行,内错角相等)
∠2=∠B(两直线平行,同位角相等)
∠1+∠2+∠ACB=180°
∠A+∠B+∠ACB=180°
证明命题的一般步骤:
回顾与思考
?
(1)根据题意,画出图形;
(2)分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论;
(3)在“证明”中写出推理过程.
依据思路,运用数学符号和数学语言条理清晰地写出证明过程;检查表达过程是否正确、完善.
关于辅助线:
3、添加辅助线,可构造新图形,形成新关系,找到联系已知与未知的桥梁,把问题转化,要根据需要而定,平时做题时要注意总结.
2、它的作用是把分散的条件集中,把隐含的条件显现出来,起到牵线搭桥的作用.
1、辅助线是为了证明需要在原图上添画的线.(辅助线通常画成虚线)
三角形内角和定理:三角形的三个内角的和等于180°.
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
推论:
已知:
求证:
证明:
如图,∠ACD是△ABC的一个外角
∠ACD
=∠A+∠B
A
B
C
D
1、三角形内角和定理
三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.
A
B
C
3、三角形的一个外角大于任何一个和它不相邻的内角
2、三角形的一个外角等于和它不相邻的两个内角的和
A
B
C
1
2
D
E
∵
∠ACD
是△ABC的一个外角
∴∠ACD
=
∠A+∠B
∵
∠ACD
是△ABC的一个外角
∴
∠ACD>∠A,
∠ACD>∠B
三角形内角和定理的几何表述:
1、在△ABC中,以A为顶点的一个外角为120°,∠B=50°,则∠C=
°,请说明理由.
2、如图,比较∠1与∠2+∠3的大小,并证明你的判断.
A
B
C
D
70
B
A
C
D
E
1
2
3
做一做
本节课你学到什么?
已知命题:如图,点A,D,B,E在同一直线上,且AD=BE,AC∥DF,则△ABC≌△DEF.这个命题是真命题还是假命题?
A
D
B
E
C
F
如果是真命题,请给出证明;
如果是假命题,请添加适当的条件,使它成为真命题.你有几种不同的添加方法?
A
B
C
E
图1
E
A
B
C
D
F
图2
A
N
B
C
T
S
图3
P
Q
R
M
A
N
B
C
T
S
图4
P
Q
R
M
A
B
C
对于三角形,我们已经有哪些认识?
合作探索
定义
分类
内角和
…………
三角形的三个内角的和等于180°.
例1、求证:
A
B
C
已知:
求证:
如图,∠A,∠B,∠C是△ABC的三个内角.
∠A+∠B+∠C=180°
实验1:先将纸片三角形一角折向其对边,使顶点落在对边上,折线与对边平行(图1),然后把另处两角相向对折,使其顶点与已折角的顶点相嵌合(图2)、(图3),最后得到(图4)所示的结果。
A
C
B
图1
B
A
C
图2
BA
C
图3
BAC
图4
例1、求证:三角形三个内角的和等于180?.
1
1
2
A
B
D
2
3
C
1
2
实验2:
将纸片三角形顶角剪下,随意将它们拼凑在一起。
在证明三角形内角和时,小明的想法是把三个角“凑”到A处,他过点A作直线DE//BC,(如图)。他的想法可行吗?
A
B
C
E
D
证明 过点A作DE∥BC.则
∠C=∠CAE,∠B=∠BAD(两直线平行,内错角相等)
∴∠BAC+∠B+∠C=∠BAC+∠BAD+∠CAE
=∠DAE=180?(平角的定义)
你还有其他的证明方法么?
辅助线
已知:如图,
△ABC.
求证:
∠A+∠B+∠C=180°
A
B
C
1
2
D
E
证明:
作BC的延长线CD,过点C作射线CE//AB,则
∠1=∠A(两直线平行,内错角相等)
∠2=∠B(两直线平行,同位角相等)
∠1+∠2+∠ACB=180°
∠A+∠B+∠ACB=180°
证明命题的一般步骤:
回顾与思考
?
(1)根据题意,画出图形;
(2)分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论;
(3)在“证明”中写出推理过程.
依据思路,运用数学符号和数学语言条理清晰地写出证明过程;检查表达过程是否正确、完善.
关于辅助线:
3、添加辅助线,可构造新图形,形成新关系,找到联系已知与未知的桥梁,把问题转化,要根据需要而定,平时做题时要注意总结.
2、它的作用是把分散的条件集中,把隐含的条件显现出来,起到牵线搭桥的作用.
1、辅助线是为了证明需要在原图上添画的线.(辅助线通常画成虚线)
三角形内角和定理:三角形的三个内角的和等于180°.
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
推论:
已知:
求证:
证明:
如图,∠ACD是△ABC的一个外角
∠ACD
=∠A+∠B
A
B
C
D
1、三角形内角和定理
三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.
A
B
C
3、三角形的一个外角大于任何一个和它不相邻的内角
2、三角形的一个外角等于和它不相邻的两个内角的和
A
B
C
1
2
D
E
∵
∠ACD
是△ABC的一个外角
∴∠ACD
=
∠A+∠B
∵
∠ACD
是△ABC的一个外角
∴
∠ACD>∠A,
∠ACD>∠B
三角形内角和定理的几何表述:
1、在△ABC中,以A为顶点的一个外角为120°,∠B=50°,则∠C=
°,请说明理由.
2、如图,比较∠1与∠2+∠3的大小,并证明你的判断.
A
B
C
D
70
B
A
C
D
E
1
2
3
做一做
本节课你学到什么?
已知命题:如图,点A,D,B,E在同一直线上,且AD=BE,AC∥DF,则△ABC≌△DEF.这个命题是真命题还是假命题?
A
D
B
E
C
F
如果是真命题,请给出证明;
如果是假命题,请添加适当的条件,使它成为真命题.你有几种不同的添加方法?
A
B
C
E
图1
E
A
B
C
D
F
图2
A
N
B
C
T
S
图3
P
Q
R
M
A
N
B
C
T
S
图4
P
Q
R
M
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
