浙教版八上5.5 一次函数的简单应用 课件(26张)
文档属性
| 名称 | 浙教版八上5.5 一次函数的简单应用 课件(26张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 16:55:23 | ||
图片预览





文档简介
(共26张PPT)
一次函数的简单应用
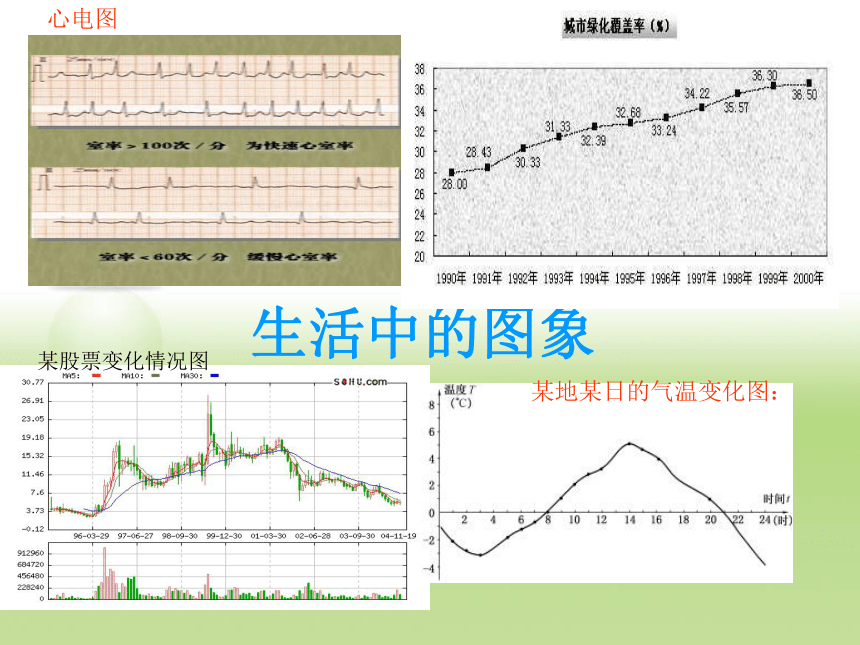
生活中的图象
某股票变化情况图
心电图
某地某日的气温变化图:
2
4
6
8
10
12
14
16
18
20
22
24
2
4
6
8
10
T℃
-2
0
某地某日的气温变化图:
t(h)
北京春季某一天的气温曲线图
物质的溶解度曲线图
股票走势曲线图
(2)圣诞老人去超市途中的速度是多少?回家途中的速度是多少?
(1)圣诞老人在超市逗留了多少时间?
(4)圣诞老人在来去的途中,离家1km处的时间是几时几分?
(3)用恰当的方式表示圣诞老人离家的路程s(千米)和所经过的时间t(分)之间的函数关系。
例1圣诞老人上午8:00从家里出发,骑车去超市购物,然后从超市返回家中。圣诞老人离家的路程s(千米)和所经过的时间t(分)之间的函数关系如图所示,请根据图象回答下列问题:
10
20
30
40
50
60
70
O
t(分)
s(千米)
1
2
A
C
B
x(单位:
份)
y(单位:元)
O
100
200
300
400
500
600
1000
4000
5000
2000
3000
6000
如图,L
反映了某商场圣诞礼品的销售收入与销售量的关系,L
反映了该商场圣诞礼品的销售成本与销售量的关系,根据图意填空:
L1
L2
(1)当销售量为200份时,销售收入= 元,
销售成本= 元;
2000
3000
x(单位:份)
y(单位:元)
O
100
200
300
400
500
600
1000
4000
5000
2000
3000
6000
L1
L2
(2)当销售量为600份时,销售收入= 元,
销售成本= 元;
6000
5000
(3)当销售量为
时,销售收入等于销售成本;
400份
(L
1反映销售收入与销售量的关系
,L2
反映了销售成本与销售量的关系)
x(单位:份)
y(单位:元)
O
100
200
300
400
500
600
1000
4000
5000
2000
3000
6000
L1
L2
(4)当销售量
时,该商场赢利(收入大于成本)
当销售量
时,该商场亏损(收入小于成本)
X>400
X<400
(5)
L1对应的函数表达式是 ,
L2对应的函数表达式是 。
y1=10x
y2=5x+2000
L
1
反映销售收入
与销售量的关系
L
2
反映了销售成本
与销售量的关系
鞋长单位:cm
例2圣诞老人买了很多鞋,送给小明全家每人一双,鞋长和鞋码如下表,你能知道小明的鞋码吗?
爷爷
奶奶
爸爸
妈妈
哥哥
姐姐
小明
鞋长
…
25.5
23
26.5
23.5
26
24
25
…
鞋码
…
41
36
43
37
42
38
?
…
40
41
37
36
38
39
(cm)
42
43
0
x
y(码)
23
24
25
26
27
?
?
?
?
?
?
当x=25.5时,y=41;当x=23时,y=36
得
当x=25时,y=2×25-10
=40
解:设x表示鞋长,y表示鞋码,由题意,得
y=kx+b
解得
∴
y=2x-10
爷爷
奶奶
爸爸
妈妈
哥哥
姐姐
小明
鞋长
…
25.5
23
26.5
23.5
26
24
25
…
鞋码
…
41
36
43
37
42
38
?
…
鞋长单位:cm
当x=25.5时,y=41;当x=23时,y=36
得
当x=25时,y=2×25-10
=40
解:设x表示鞋长,y表示鞋码,由题意,得
y=kx+b
解得
∴
y=2x-10
爷爷
奶奶
爸爸
妈妈
哥哥
姐姐
小明
鞋长
…
25.5
23
26.5
23.5
26
24
25
…
鞋码
…
41
36
43
37
42
38
40
…
鞋长单位:cm
例3 柴油机在工作时油箱中的余油量Q(千克)
与工作时间t(小时)成一次函数关系,当工作开始时
油箱中有油40千克,工作3.5小时后,油箱中余油22.5
千克(1)写出余油量Q与时间t的函数关系式;(2)画出
这个函数的图象。
解:(1)设Q=kt+b。把t=0,Q=40;t=3.5,Q=22.5
分别代入上式,得
解得
解析式为:Q=-5t+40 (0≤t≤8)
(2)、取t=0,得Q=40;取t=8,得Q=0。描出点
A(0,40),B(8,0)。然后连成线段AB即是所
求的图形。
点评:(1)求出函数关系式时,
必须找出自变量的取值范围。
(2)画函数图象时,应
根据函数自变量的取值范围来
确定图象的范围。
20
40
8
0
t
Q
图象是包括
两端点的线段
.
.
A
B
1.某商场文具部的某种笔售价25元,练习本每本售价5元。该商场为了促销制定了两种优惠方案供顾客选择。甲:买一支笔赠送一本练习本。乙:按购买金额打九折付款。某校欲购这种笔10支,练习本x(x
≥10)本,如何选择方案购买呢?
解:甲、乙两种方案的实际金额y元与练习本x本之间的关系式是:
y甲=(x-10)××5+25×10=5x+200
(x
≥10)
y乙=(10×25+5x)
×0.9=4.5x+225
(x
≥10)
解方程组
y=5x+200
y=4.5x+225
得
x=50
y=450
o
x
y
10
50
200
由图象可以得出同样结果
当10
≤
x<50时,y甲当x=50时,y甲=y乙
当x>50时,y甲>y乙
所以我的建议为:……
2.根据市场调查分析,某蔬菜基地准备安排40个劳动力,用10公顷地种黄瓜、西红柿和青菜,且青菜至少种2公顷,种植这三种菜所需劳动力和预计产值如下表:
蔬菜品种
黄瓜
西红柿
青菜
每公顷需劳动力(个)
5
15/4
5/2
每公顷产值(千元)
22.5
18
12
问怎样安排种植面积和分配劳力,使预计的总产值最高?
解:设黄瓜、西红柿、青菜的种植面积分别为x、y、z公顷,总产值为p千元。
即:
x+y+z=10
5x+(15/4)y+(5/2)z=40
x>0,
y>0,
z
≥
0
y=-2x+12
z=x-2
4
≤x<6
p=22.5x+18y+12z=-1.5x+192
所以当x=4时,总产值p最高为186千元。
此时黄瓜、西红柿、青菜的种植面积分别为4、4、2公顷,各安排的劳动力分别为20、15、5个。
某军加油飞机接到命令,立即给另一架正在飞行的运输飞机进行空中加油.在加油的过程中,设运输飞机的油箱余油量为Q1吨,加油飞机的加油油箱的余油量为Q2吨(不包括其自身用油),加油时间为t分钟,Q1、Q2与t之间的函数图象如图所示,结合图象回答下列问题:
(1)加油飞机的加油油箱中装载了多少吨油?将这些油全部加给运输飞机需要多少分钟?
解
(1)由图象知,加油飞机的加油油箱中装载了30吨油,全部加给运输飞机需10分钟.
(2)求加油过程中,运输飞机的余油量Q1(吨)与时间t(分钟)的函数关系式;
解:(2)设Q1=kt+b,把(0,40)和(10,69)代入,得
解得
所以Q1=2.9t+40(0≤t≤10).
由于水资源缺乏,两地不得不从黄河的扬水站A处引水,这就需要在A、B、C之间铺设地下输水管道。现设计了三种铺设方案。如图(1)、(2)、(3),图中实线部分表示管道铺设线路。在图(2)中,AD⊥BC于D,在图(3)中,OA=OB=OC,为减少渗漏,节约水资源,并降低工程造价,铺设线路应尽量缩短。已知△ABC恰好是一个边长为a的等边三角形,请你通过计算说明哪种铺设方案好?
研讨:
A
C
B
(1)
(2)
B
C
A
D
O
(3)
B
C
A
学校搞绿化,需要在一块矩形空地上建花坛(如图),现征集设计方案,要求设计的图案由圆和正方形组成,(圆和正方形的个数不限),且使整个矩形场地成轴对称图形,请你在左边的矩形中画出你的设计方案。
研讨:
观察下列图象,你能设计适当的实际情景吗
试一试
(1)若家和乙地之间相距650千米则摩托车能顺利到达吗?
(2)油箱中剩余油量小于0.8升时,摩托车会自动报警,那多少千米后,摩托车会自动报警?
若图象反映了摩托车油箱的剩余油量y(升)和摩托车行驶路程x(千米)之间
的关系.
小明骑摩托车从家到乙地,摩托车油箱最多储油10升
y/升
x/千米
仔细观察图象
原图
应用与延伸
如果摩托车油箱的剩余油量y(升)和摩托车行驶路程x(千米)之间
的关系变为图1:
图1
观察图1设想一下发生了什么情况?
⑴加油站在哪里?加油多少升?
⑵加油前每100千米耗油多少?加油后呢?
⑶若乙地与加油站之间还有250千米,要到达乙地所加的油是否够用?
图2
若变为图2呢?观察图象变化,你看出了些什么?
设想一下此时又发生了什么情况?
对与实际问题进行:
收集数据;
画出函数的图象;
判断函数的类型;
求出解析式.
就是一个建立数学模型的过程.
两个重要的知识块:
二:建立数学模型解决实际问题
一:利用函数图象解决实际问题
一次函数的简单应用
生活中的图象
某股票变化情况图
心电图
某地某日的气温变化图:
2
4
6
8
10
12
14
16
18
20
22
24
2
4
6
8
10
T℃
-2
0
某地某日的气温变化图:
t(h)
北京春季某一天的气温曲线图
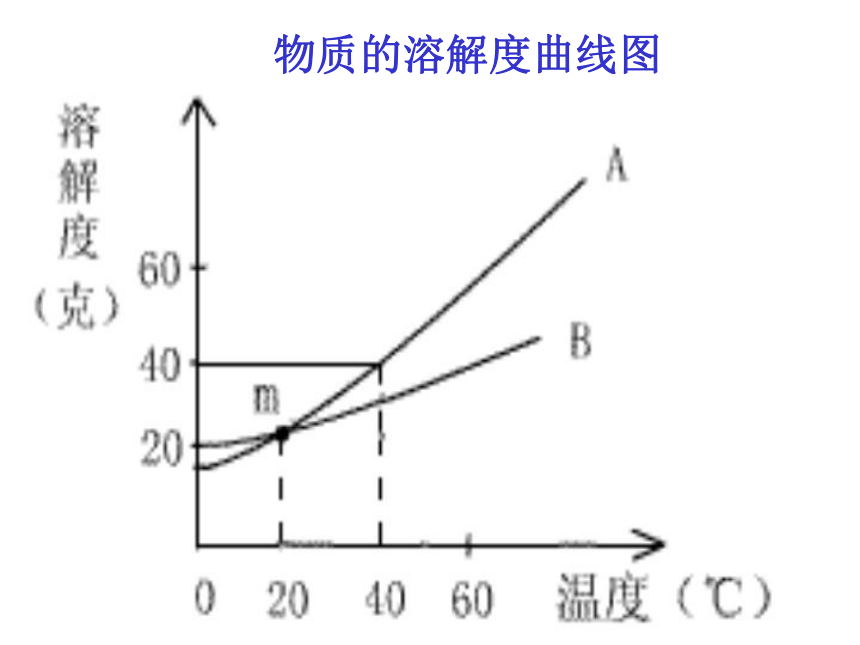
物质的溶解度曲线图
股票走势曲线图
(2)圣诞老人去超市途中的速度是多少?回家途中的速度是多少?
(1)圣诞老人在超市逗留了多少时间?
(4)圣诞老人在来去的途中,离家1km处的时间是几时几分?
(3)用恰当的方式表示圣诞老人离家的路程s(千米)和所经过的时间t(分)之间的函数关系。
例1圣诞老人上午8:00从家里出发,骑车去超市购物,然后从超市返回家中。圣诞老人离家的路程s(千米)和所经过的时间t(分)之间的函数关系如图所示,请根据图象回答下列问题:
10
20
30
40
50
60
70
O
t(分)
s(千米)
1
2
A
C
B
x(单位:
份)
y(单位:元)
O
100
200
300
400
500
600
1000
4000
5000
2000
3000
6000
如图,L
反映了某商场圣诞礼品的销售收入与销售量的关系,L
反映了该商场圣诞礼品的销售成本与销售量的关系,根据图意填空:
L1
L2
(1)当销售量为200份时,销售收入= 元,
销售成本= 元;
2000
3000
x(单位:份)
y(单位:元)
O
100
200
300
400
500
600
1000
4000
5000
2000
3000
6000
L1
L2
(2)当销售量为600份时,销售收入= 元,
销售成本= 元;
6000
5000
(3)当销售量为
时,销售收入等于销售成本;
400份
(L
1反映销售收入与销售量的关系
,L2
反映了销售成本与销售量的关系)
x(单位:份)
y(单位:元)
O
100
200
300
400
500
600
1000
4000
5000
2000
3000
6000
L1
L2
(4)当销售量
时,该商场赢利(收入大于成本)
当销售量
时,该商场亏损(收入小于成本)
X>400
X<400
(5)
L1对应的函数表达式是 ,
L2对应的函数表达式是 。
y1=10x
y2=5x+2000
L
1
反映销售收入
与销售量的关系
L
2
反映了销售成本
与销售量的关系
鞋长单位:cm
例2圣诞老人买了很多鞋,送给小明全家每人一双,鞋长和鞋码如下表,你能知道小明的鞋码吗?
爷爷
奶奶
爸爸
妈妈
哥哥
姐姐
小明
鞋长
…
25.5
23
26.5
23.5
26
24
25
…
鞋码
…
41
36
43
37
42
38
?
…
40
41
37
36
38
39
(cm)
42
43
0
x
y(码)
23
24
25
26
27
?
?
?
?
?
?
当x=25.5时,y=41;当x=23时,y=36
得
当x=25时,y=2×25-10
=40
解:设x表示鞋长,y表示鞋码,由题意,得
y=kx+b
解得
∴
y=2x-10
爷爷
奶奶
爸爸
妈妈
哥哥
姐姐
小明
鞋长
…
25.5
23
26.5
23.5
26
24
25
…
鞋码
…
41
36
43
37
42
38
?
…
鞋长单位:cm
当x=25.5时,y=41;当x=23时,y=36
得
当x=25时,y=2×25-10
=40
解:设x表示鞋长,y表示鞋码,由题意,得
y=kx+b
解得
∴
y=2x-10
爷爷
奶奶
爸爸
妈妈
哥哥
姐姐
小明
鞋长
…
25.5
23
26.5
23.5
26
24
25
…
鞋码
…
41
36
43
37
42
38
40
…
鞋长单位:cm
例3 柴油机在工作时油箱中的余油量Q(千克)
与工作时间t(小时)成一次函数关系,当工作开始时
油箱中有油40千克,工作3.5小时后,油箱中余油22.5
千克(1)写出余油量Q与时间t的函数关系式;(2)画出
这个函数的图象。
解:(1)设Q=kt+b。把t=0,Q=40;t=3.5,Q=22.5
分别代入上式,得
解得
解析式为:Q=-5t+40 (0≤t≤8)
(2)、取t=0,得Q=40;取t=8,得Q=0。描出点
A(0,40),B(8,0)。然后连成线段AB即是所
求的图形。
点评:(1)求出函数关系式时,
必须找出自变量的取值范围。
(2)画函数图象时,应
根据函数自变量的取值范围来
确定图象的范围。
20
40
8
0
t
Q
图象是包括
两端点的线段
.
.
A
B
1.某商场文具部的某种笔售价25元,练习本每本售价5元。该商场为了促销制定了两种优惠方案供顾客选择。甲:买一支笔赠送一本练习本。乙:按购买金额打九折付款。某校欲购这种笔10支,练习本x(x
≥10)本,如何选择方案购买呢?
解:甲、乙两种方案的实际金额y元与练习本x本之间的关系式是:
y甲=(x-10)××5+25×10=5x+200
(x
≥10)
y乙=(10×25+5x)
×0.9=4.5x+225
(x
≥10)
解方程组
y=5x+200
y=4.5x+225
得
x=50
y=450
o
x
y
10
50
200
由图象可以得出同样结果
当10
≤
x<50时,y甲
当x>50时,y甲>y乙
所以我的建议为:……
2.根据市场调查分析,某蔬菜基地准备安排40个劳动力,用10公顷地种黄瓜、西红柿和青菜,且青菜至少种2公顷,种植这三种菜所需劳动力和预计产值如下表:
蔬菜品种
黄瓜
西红柿
青菜
每公顷需劳动力(个)
5
15/4
5/2
每公顷产值(千元)
22.5
18
12
问怎样安排种植面积和分配劳力,使预计的总产值最高?
解:设黄瓜、西红柿、青菜的种植面积分别为x、y、z公顷,总产值为p千元。
即:
x+y+z=10
5x+(15/4)y+(5/2)z=40
x>0,
y>0,
z
≥
0
y=-2x+12
z=x-2
4
≤x<6
p=22.5x+18y+12z=-1.5x+192
所以当x=4时,总产值p最高为186千元。
此时黄瓜、西红柿、青菜的种植面积分别为4、4、2公顷,各安排的劳动力分别为20、15、5个。
某军加油飞机接到命令,立即给另一架正在飞行的运输飞机进行空中加油.在加油的过程中,设运输飞机的油箱余油量为Q1吨,加油飞机的加油油箱的余油量为Q2吨(不包括其自身用油),加油时间为t分钟,Q1、Q2与t之间的函数图象如图所示,结合图象回答下列问题:
(1)加油飞机的加油油箱中装载了多少吨油?将这些油全部加给运输飞机需要多少分钟?
解
(1)由图象知,加油飞机的加油油箱中装载了30吨油,全部加给运输飞机需10分钟.
(2)求加油过程中,运输飞机的余油量Q1(吨)与时间t(分钟)的函数关系式;
解:(2)设Q1=kt+b,把(0,40)和(10,69)代入,得
解得
所以Q1=2.9t+40(0≤t≤10).
由于水资源缺乏,两地不得不从黄河的扬水站A处引水,这就需要在A、B、C之间铺设地下输水管道。现设计了三种铺设方案。如图(1)、(2)、(3),图中实线部分表示管道铺设线路。在图(2)中,AD⊥BC于D,在图(3)中,OA=OB=OC,为减少渗漏,节约水资源,并降低工程造价,铺设线路应尽量缩短。已知△ABC恰好是一个边长为a的等边三角形,请你通过计算说明哪种铺设方案好?
研讨:
A
C
B
(1)
(2)
B
C
A
D
O
(3)
B
C
A
学校搞绿化,需要在一块矩形空地上建花坛(如图),现征集设计方案,要求设计的图案由圆和正方形组成,(圆和正方形的个数不限),且使整个矩形场地成轴对称图形,请你在左边的矩形中画出你的设计方案。
研讨:
观察下列图象,你能设计适当的实际情景吗
试一试
(1)若家和乙地之间相距650千米则摩托车能顺利到达吗?
(2)油箱中剩余油量小于0.8升时,摩托车会自动报警,那多少千米后,摩托车会自动报警?
若图象反映了摩托车油箱的剩余油量y(升)和摩托车行驶路程x(千米)之间
的关系.
小明骑摩托车从家到乙地,摩托车油箱最多储油10升
y/升
x/千米
仔细观察图象
原图
应用与延伸
如果摩托车油箱的剩余油量y(升)和摩托车行驶路程x(千米)之间
的关系变为图1:
图1
观察图1设想一下发生了什么情况?
⑴加油站在哪里?加油多少升?
⑵加油前每100千米耗油多少?加油后呢?
⑶若乙地与加油站之间还有250千米,要到达乙地所加的油是否够用?
图2
若变为图2呢?观察图象变化,你看出了些什么?
设想一下此时又发生了什么情况?
对与实际问题进行:
收集数据;
画出函数的图象;
判断函数的类型;
求出解析式.
就是一个建立数学模型的过程.
两个重要的知识块:
二:建立数学模型解决实际问题
一:利用函数图象解决实际问题
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
