浙教版八上5.5 一次函数的简单应用(1) 课件(12张)
文档属性
| 名称 | 浙教版八上5.5 一次函数的简单应用(1) 课件(12张) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 16:56:00 | ||
图片预览




文档简介
(共13张PPT)
浙
教
版
八年级
上册
(1)填一填:
正方形个数x
火柴棒根数y
1
2
3
4
5
4
7
10
13
16
……
(2)根据表格中的数据你能直接找到变量x与y的关系吗?
y=3x+1
引入篇:
解析式
列表
图象
函数的三种表示法
新知篇:
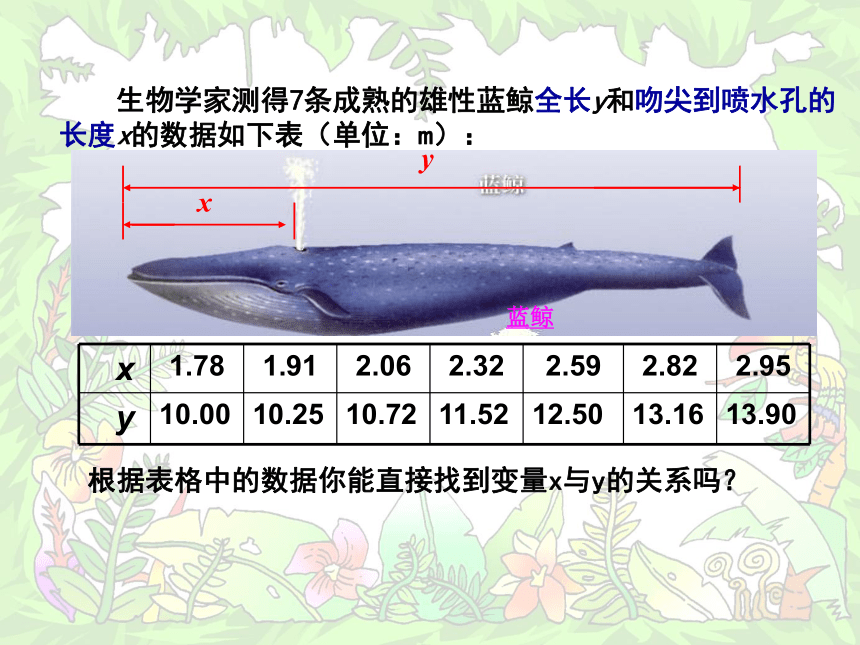
生物学家测得7条成熟的雄性蓝鲸全长y和吻尖到喷水孔的长度x的数据如下表(单位:m):
x
1.78
1.91
2.06
2.32
2.59
2.82
2.95
y
10.00
10.25
10.72
11.52
12.50
13.16
13.90
x
蓝鲸
y
根据表格中的数据你能直接找到变量x与y的关系吗?
一次函数
特征
特征
解析式为y=kx+b
图象是一条直线
一次函数
判断
判断
怎样判断“两个变量是否满足一次函数的关系?”
图象是一条直线
解析式为y=kx+b
数
形
数?
形?
X(m)
y(m)
0
1
2
3
4
2
4
6
8
10
12
14
16
18
x
1.78
1.91
2.06
2.32
2.59
2.82
2.95
y
10.00
10.25
10.72
11.52
12.50
13.16
13.90
1.建立直角坐标系,描点
2.观察这些点的趋势大致在
一条直线上,
3.关系式能求吗?该怎么求?
能否利用某种函数刻画这两个变量x和y的关系?
图象
列表
进而判断y是关于x的一次函数。
解:
设这个一次函数的解析式为y=kx+b,
把点(1.91,10.25),(2.59,12.50)的坐标代入
得
10.25=1.91k+b
12.50=2.59k+b
解得
k≈3.31
b≈3.93
∴所求函数解析式为y=3.31x+3.93
注意:这样获得的函数解析式是近似的
待定系数法
数形结合
确定两个变量是否构成一次函数关系的一种常用方法是:
实验
数据
函数类型
图象
获取
数据
图象
画出
判断
用待定系数法求出函数解析式
数学建模
每一个人的身高y与其指距x满足怎样的函数关系呢?
实践篇:
在实验中获得数据,填入下表:
身高y(cm)
指距x(cm)
指距是指大拇指与小拇指尽量张开
时,两指间的距离
姚明身高226厘米,
则他的指距为多少?
人是千差万别,有的高有的矮,但是研究表明,一般情况下人的身高是指距的一次函数.
实践篇:
实验数据
画出图像
判断类型
求解析式
实际生活
解释、解决
通过这节课的学习,我们学习到了
4个步骤:
梳理篇:
1个过程:
2个数学思想:
3个环节:
实验
数学建模
搭火柴棒、蓝鲸问题、指距问题
数形结合,
建模思想
数据
图象
函数
浙
教
版
八年级
上册
(1)填一填:
正方形个数x
火柴棒根数y
1
2
3
4
5
4
7
10
13
16
……
(2)根据表格中的数据你能直接找到变量x与y的关系吗?
y=3x+1
引入篇:
解析式
列表
图象
函数的三种表示法
新知篇:
生物学家测得7条成熟的雄性蓝鲸全长y和吻尖到喷水孔的长度x的数据如下表(单位:m):
x
1.78
1.91
2.06
2.32
2.59
2.82
2.95
y
10.00
10.25
10.72
11.52
12.50
13.16
13.90
x
蓝鲸
y
根据表格中的数据你能直接找到变量x与y的关系吗?
一次函数
特征
特征
解析式为y=kx+b
图象是一条直线
一次函数
判断
判断
怎样判断“两个变量是否满足一次函数的关系?”
图象是一条直线
解析式为y=kx+b
数
形
数?
形?
X(m)
y(m)
0
1
2
3
4
2
4
6
8
10
12
14
16
18
x
1.78
1.91
2.06
2.32
2.59
2.82
2.95
y
10.00
10.25
10.72
11.52
12.50
13.16
13.90
1.建立直角坐标系,描点
2.观察这些点的趋势大致在
一条直线上,
3.关系式能求吗?该怎么求?
能否利用某种函数刻画这两个变量x和y的关系?
图象
列表
进而判断y是关于x的一次函数。
解:
设这个一次函数的解析式为y=kx+b,
把点(1.91,10.25),(2.59,12.50)的坐标代入
得
10.25=1.91k+b
12.50=2.59k+b
解得
k≈3.31
b≈3.93
∴所求函数解析式为y=3.31x+3.93
注意:这样获得的函数解析式是近似的
待定系数法
数形结合
确定两个变量是否构成一次函数关系的一种常用方法是:
实验
数据
函数类型
图象
获取
数据
图象
画出
判断
用待定系数法求出函数解析式
数学建模
每一个人的身高y与其指距x满足怎样的函数关系呢?
实践篇:
在实验中获得数据,填入下表:
身高y(cm)
指距x(cm)
指距是指大拇指与小拇指尽量张开
时,两指间的距离
姚明身高226厘米,
则他的指距为多少?
人是千差万别,有的高有的矮,但是研究表明,一般情况下人的身高是指距的一次函数.
实践篇:
实验数据
画出图像
判断类型
求解析式
实际生活
解释、解决
通过这节课的学习,我们学习到了
4个步骤:
梳理篇:
1个过程:
2个数学思想:
3个环节:
实验
数学建模
搭火柴棒、蓝鲸问题、指距问题
数形结合,
建模思想
数据
图象
函数
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
