浙教版九上3.5.1 圆周角 教案

3.5
圆周角
（第1课时）
教学目标：
1、理解圆周角的概念，会识别圆周角。
2、掌握圆周角定理，并会此定理进行简单的论证和计算。
3、初步体会、理解分类讨论、转化、完全归纳法等数学
思想方法。
重点：圆周角的概念和圆周角定理。
难点：用分类讨论思想证明圆周角定理。
教学设计：
活动1、创设情境，引入新课
一、如图,
在足球比赛中，甲，乙,丙三名同学分别在B,D,E三处，他们都说在自己所在位置所对球门AC的张角大，为此，他们出现了不同的说法，你认为他们谁说的对？（引出课题）
二、知识准备
1、三角形的外角定理
2、圆心角的概念
活动2：类比联想，理解概念
一、圆周角的定义：
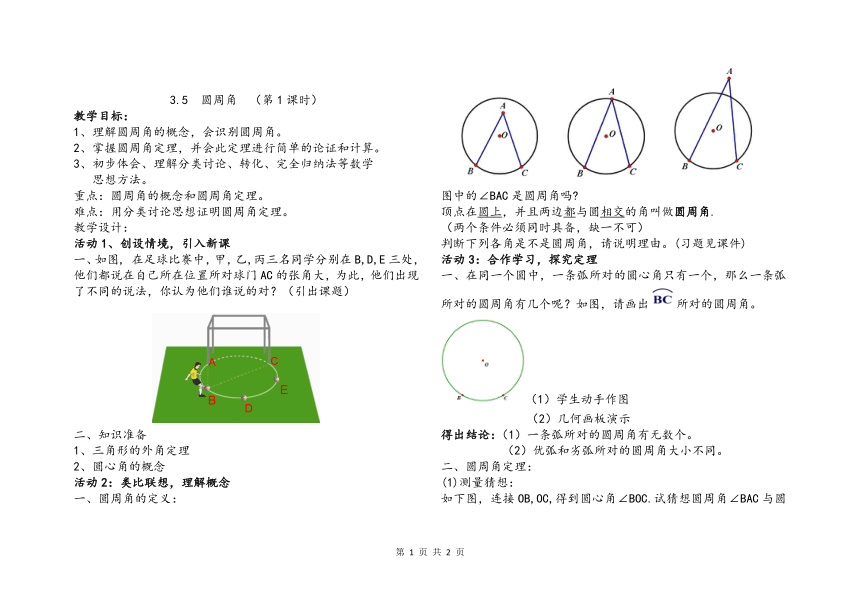
图中的∠BAC是圆周角吗?
顶点在圆上，并且两边都与圆相交的角叫做圆周角.
（两个条件必须同时具备，缺一不可）
判断下列各角是不是圆周角，请说明理由。(习题见课件)
活动3：合作学习，探究定理
一、在同一个圆中，一条弧所对的圆心角只有一个，那么一条弧所对的圆周角有几个呢？如图，请画出所对的圆周角。
（1）学生动手作图
（2）几何画板演示
得出结论：（1）一条弧所对的圆周角有无数个。
（2）优弧和劣弧所对的圆周角大小不同。
二、圆周角定理：
(1)测量猜想：
如下图，连接OB,OC,得到圆心角∠BOC.试猜想圆周角∠BAC与圆心∠BOC存在怎样的数量关系.
(2)推导论证：
（1）
（2）
（3）
据此，定理的证明应分三种情况分别证明：
（1）当圆心O在圆周角的一边上时；如图（1）
OA=OC
∴
∠A=
∠C
∴
∠BOC=
∠
A+
∠C
=2∠A
∴
∠A=∠BOC
（2）当圆心O在圆周角的内部时，如图（2）作直径AD，将问题转化为（1）的基本图形进行证明
（3）当圆心O在圆周角的外部时；如图（3）作直径AD，将问题转化为（1）中的图形，进行证明
由学生完成（2）、（3）的证明
通过（1）、（2）、（3）的证明，得出圆周角定理：
一条弧所对的圆周角等于它所对圆心角的一半
活动四：学以致用
用所学定理解决,在足球比赛中，甲，乙,丙三名同学分别在B,D,E三处，他们都说在自己所在位置所对球门AC的张角大，为此，他们出现了不同的说法，你认为他们谁说的对？
活动五：基础训练，应用定理
拆红包，课件显示对应红包中的习题
小结：
B
D
E
A
C
A
通过几何画板展示，计算出∠BAC=（
）∠BOC
量出∠BAC=（
）
量出∠BOC=（
）
得出：∠BAC=（
）∠BOC
图（3）
图（1）
图（2）
圆周角定义
圆心角
类比
圆周角
1.顶点在圆上
2.两边都与圆相交
（二者必须同时具备）
一条弧所对的圆周角都等于它所对的圆心角的一半。
转化、分类讨论、一般到特殊，完全归纳法等
圆周角定理
多种思想方法