浙教版九上1.2.1二次函数的图像 教案(表格式)
文档属性
| 名称 | 浙教版九上1.2.1二次函数的图像 教案(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 889.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 00:00:00 | ||
图片预览

文档简介
浙教版数学九年级上册1.2.1课时教学设计
课题
二次函数
单元
1
学科
数学
年级
九
学习目标
情感态度和价值观目标
进一步培养数形结合方法研究函数的性质
能力目标
1.经历描点法画函数图像的过程2.经历从特殊到一般的认识过程,学会合情推理
知识目标
1.
了解二次函数图像的概念2.
学会用描点法画y=ax2图像。3.学会观察、归纳、概括函数图像的特征4.
掌握y=ax2图像的位置关系及有关性质
重点
函数
y=ax2型二次函数的描绘和图像特征的归纳
难点
选择适当的自变量和相应的函数值来画函数图像,该过程较为复杂;还有提高题实际的应用难度较高。
学法
自主探究,合作交流
教法
多媒体,问题引领
教学过程
教学环节
教师活动
学生活动
设计意图
导入新课
问题:1.
正比例函数y=kx(k
≠
0)其图像是什么2.
一次函数y=kx+b(k
≠
0)其图像又是什么3.
反比例函数(k
≠
0)其图像又是什么(学生思考后集体回答)二次函数
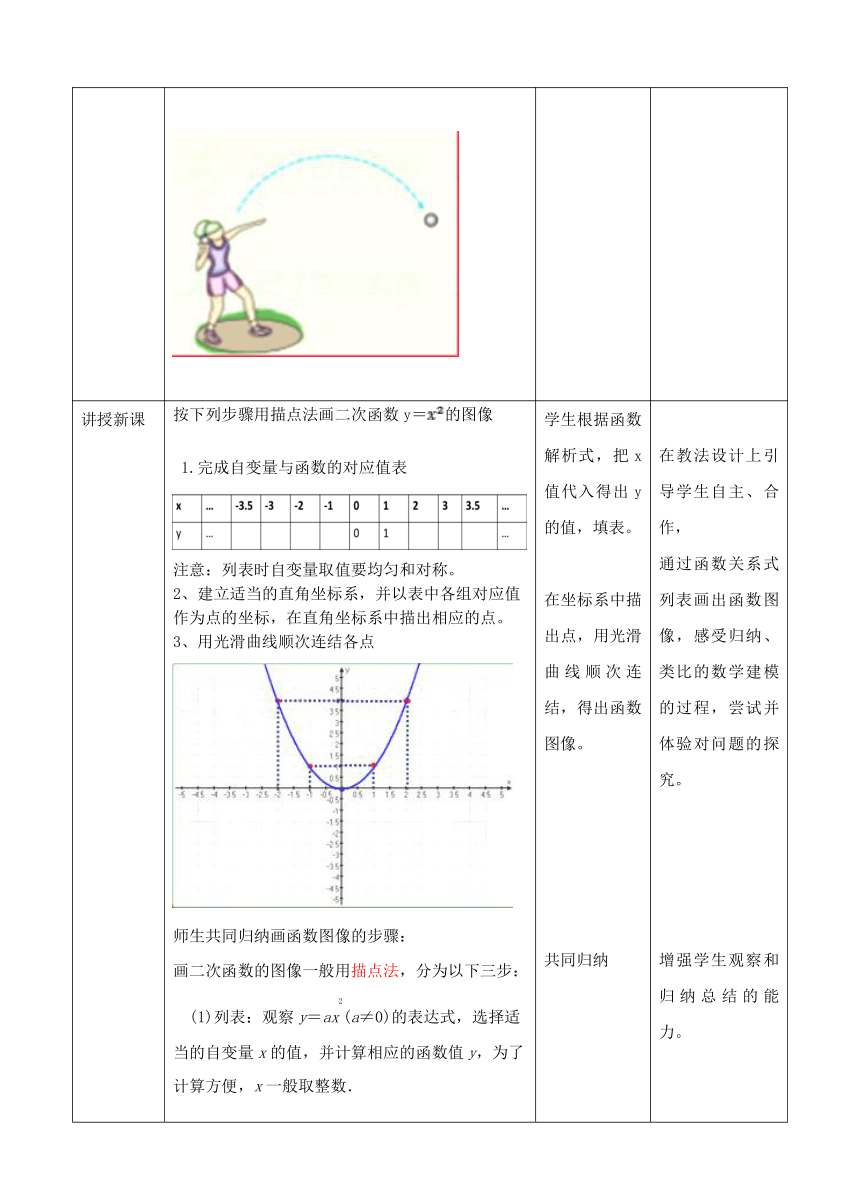
y=ax2+bx+c(a≠0)的图像又是什么?想一想:铅球推出以后沿着怎样的一条曲线运动?你能用二次函数的表达式来描述这条曲线吗?
(?http:?/??/?www.21cnjy.com?/??)
学生解答问题
学生在教师的引导下,能很快回忆相关问题,引发对新问题的思考
讲授新课
按下列步骤用描点法画二次函数y=的图像
1.完成自变量与函数的对应值表
(?http:?/??/?www.21cnjy.com?/??)注意:列表时自变量取值要均匀和对称。2、建立适当的直角坐标系,并以表中各组对应值作为点的坐标,在直角坐标系中描出相应的点。3、用光滑曲线顺次连结各点
(?http:?/??/?www.21cnjy.com?/??)师生共同归纳画函数图像的步骤:画二次函数的图像一般用描点法,分为以下三步:
(1)列表:观察y=ax2(a≠0)的表达式,选择适当的自变量x的值,并计算相应的函数值y,为了计算方便,x一般取整数.
(2)描点:在直角坐标系中描出各点;
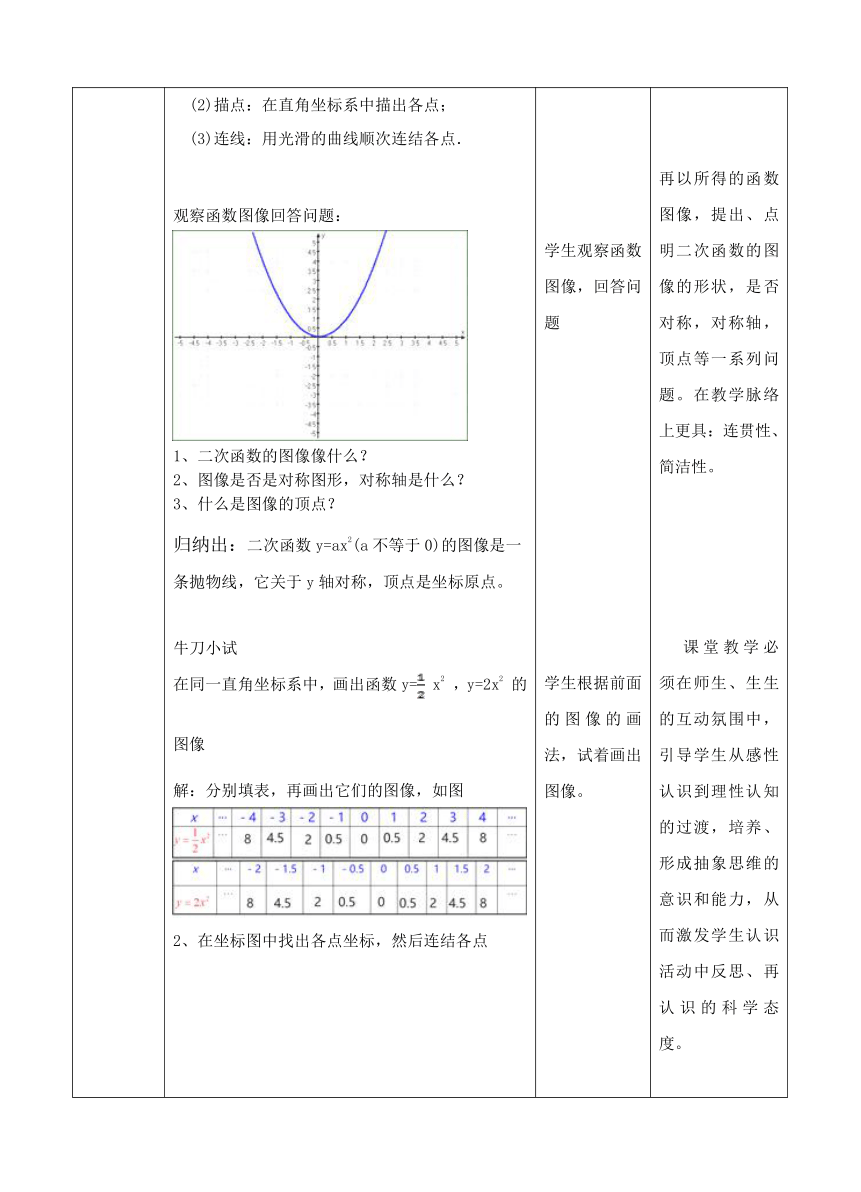
(3)连线:用光滑的曲线顺次连结各点.观察函数图像回答问题:
(?http:?/??/?www.21cnjy.com?/??)1、二次函数的图像像什么?2、图像是否是对称图形,对称轴是什么?3、什么是图像的顶点?归纳出:二次函数y=ax2(a不等于0)的图像是一条抛物线,它关于y轴对称,顶点是坐标原点。牛刀小试在同一直角坐标系中,画出函数y=
x2
,y=2x2
的图像解:分别填表,再画出它们的图像,如图
(?http:?/??/?www.21cnjy.com?/??)2、在坐标图中找出各点坐标,然后连结各点
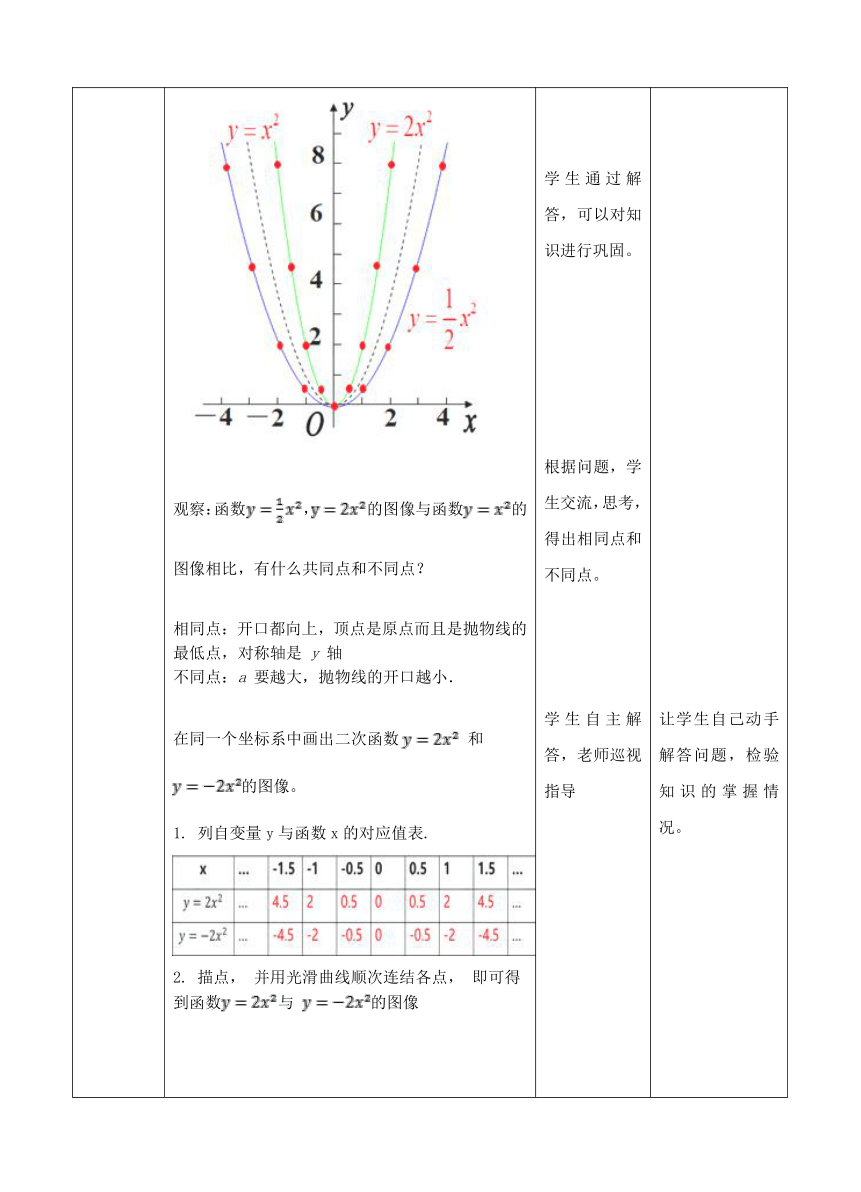
(?http:?/??/?www.21cnjy.com?/??)观察:函数,的图像与函数的图像相比,有什么共同点和不同点?相同点:开口都向上,顶点是原点而且是抛物线的最低点,对称轴是
y
轴不同点:a
要越大,抛物线的开口越小.在同一个坐标系中画出二次函数
和的图像。1.
列自变量y与函数x的对应值表.
(?http:?/??/?www.21cnjy.com?/??)2.
描点,
并用光滑曲线顺次连结各点,
即可得到函数与
的图像
(?http:?/??/?www.21cnjy.com?/??)想一想二次函数的图像与的图像关于什么对称?如果已知的图像,你认为可怎样更方便地得到的图像?填一填
(?http:?/??/?www.21cnjy.com?/??)归纳:二次函数的性质:二次函数y=ax2(a不等于0)的图像是一
(?http:?/??/?www.21cnjy.com?)条抛物线,它关于y轴对称,顶点是坐标原点。当a>0时,抛物线的开口向上,顶点是抛物线的最低点;当a<0时,抛物线的开口向下,顶点是抛物线的最高点。例1、已知二次函数y=ax2(a≠0)的图像经过点(-2,-3).
(1)求a的值,并写出这个二次函数的解析式.(2)说出这个二次函数的顶点坐标、对称轴、开口方向和图像的位置.例2、已知函数的图像是抛物线(1)求m的值;(2)当m为何值时,抛物线的开口向下?(3)当m为何值时,抛物线有最低点?并写出它的顶点坐标和对称轴。
学生根据函数解析式,把x值代入得出y的值,填表。在坐标系中描出点,用光滑曲线顺次连结,得出函数图像。共同归纳学生观察函数图像,回答问题学生根据前面的图像的画法,试着画出图像。学生通过解答,可以对知识进行巩固。根据问题,学生交流,思考,得出相同点和不同点。学生自主解答,老师巡视指导学生分组解答,师提问
学生填表格对函数图像的性质进行归纳
学生自主解答,教师适时的进行提示,并板书
在教法设计上引导学生自主、合作,通过函数关系式列表画出函数图像,感受归纳、类比的数学建模的过程,尝试并体验对问题的探究。增强学生观察和归纳总结的能力。再以所得的函数图像,提出、点明二次函数的图像的形状,是否对称,对称轴,顶点等一系列问题。在教学脉络上更具:连贯性、简洁性。课堂教学必须在师生、生生的互动氛围中,引导
(?http:?/??/?www.21cnjy.com?)学生从感性认识到理性认知的过渡,培养、形成抽象思维的意识和能力,从而激发学生认识活动中反思、再认识的科学态度。让学生自己动手解答问题,检验知识的掌握情况。培养学生解决问题的能力和归纳的能力通过例题的解答,使学生对知识的掌握进一步的提高。
巩固提升
1.如图所示的函数图像所表示的表达式有可能是( )
(?http:?/??/?www.21cnjy.com?/??)
A.y=-x2
B.y=x2C.y=x
D.答案:B2.下列各点在抛物线y=2x2上的是( )
A.(2,1)
B.(1,2)
C.(1,-2)
D.(-1,-2)答案:B3、已知二次函数y=的图像开口向下,则( )
A.m<-1 B.m=-1
C.m<1
D.m=1
答案:B4.关于二次函数y=x2的图像,下列说法错误的是( )
A.它的形状是一条抛物线
B.它的开口向上,且关于y轴对称
C.它的顶点是抛物线的最高点
D.它与y=-x2的图像关于x轴对称答案:C5、已知抛物线经过点A(-2,-8)。(1)求此抛物线的函数解析式;(2)判断点B(-1,-4)是否在此抛物线上。(3)求出此抛物线上纵坐标为-6的点的坐标。答案:解:(1)将点A(-2,-8)代入中,即:-8=4a∴a=-2∴抛物线的解析式为:(2)将点B(-1,-4)代入-4=-2,不成立∴点B不在抛物线上。(3)将-6代入解析式,即-6=-2解得:x=
±6、拱桥的形状是抛物线,其函数关系式为y=-x2,当水面离桥顶的高度为m时,(1)水面的宽度为多少米?
(2)有一艘货船,出水面的高度为5米,宽为6米,问此船能否安全通过桥洞?
(?http:?/??/?www.21cnjy.com?/??)答案:解:(1)在y=-x2中,
当y=-时,x=±5,
故水面的宽度为2×5=10米.
答:水面的宽度为10米.
(2)
∵货船宽为6米∴当x=-3,x=3时,y=∵5>3∴此船能安全通过桥洞。
学生自主解答,教师讲解答案。
鼓励
(?http:?/??/?www.21cnjy.com?)学生认真思考;发现解决问题的方法,引导学生主动地参与教学活动,发扬数学民主,让学生在独立思考、合作交流等数学活动中,培养学生合作互助意识,提高数学交流与数学表达能力。
课堂小结
1.画二次函数的图像一般用描点法,分为以下三步:
(1)列表:观察y=ax2(a≠0)的表达式,选择适当的自变量x的值,并计算相应的函数值y,为了计算方便,x一般取整数.
(2)描点:在直角坐标系中描出各点;
(3)连线:用光滑的曲线顺次连结各点.2.二次函数的性质:二次函数y=ax2(a不等于0)的图像
(?http:?/??/?www.21cnjy.com?)是一条抛物线,它关于y轴对称,顶点是坐标原点。当a>0时,抛物线的开口向上,顶点是抛物线的最低点;当a<0时,抛物线的开口向下,顶点是抛物线的最高点。
学生归纳本节所学知识
培养学生总结,归纳的能力。
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
课题
二次函数
单元
1
学科
数学
年级
九
学习目标
情感态度和价值观目标
进一步培养数形结合方法研究函数的性质
能力目标
1.经历描点法画函数图像的过程2.经历从特殊到一般的认识过程,学会合情推理
知识目标
1.
了解二次函数图像的概念2.
学会用描点法画y=ax2图像。3.学会观察、归纳、概括函数图像的特征4.
掌握y=ax2图像的位置关系及有关性质
重点
函数
y=ax2型二次函数的描绘和图像特征的归纳
难点
选择适当的自变量和相应的函数值来画函数图像,该过程较为复杂;还有提高题实际的应用难度较高。
学法
自主探究,合作交流
教法
多媒体,问题引领
教学过程
教学环节
教师活动
学生活动
设计意图
导入新课
问题:1.
正比例函数y=kx(k
≠
0)其图像是什么2.
一次函数y=kx+b(k
≠
0)其图像又是什么3.
反比例函数(k
≠
0)其图像又是什么(学生思考后集体回答)二次函数
y=ax2+bx+c(a≠0)的图像又是什么?想一想:铅球推出以后沿着怎样的一条曲线运动?你能用二次函数的表达式来描述这条曲线吗?
(?http:?/??/?www.21cnjy.com?/??)
学生解答问题
学生在教师的引导下,能很快回忆相关问题,引发对新问题的思考
讲授新课
按下列步骤用描点法画二次函数y=的图像
1.完成自变量与函数的对应值表
(?http:?/??/?www.21cnjy.com?/??)注意:列表时自变量取值要均匀和对称。2、建立适当的直角坐标系,并以表中各组对应值作为点的坐标,在直角坐标系中描出相应的点。3、用光滑曲线顺次连结各点
(?http:?/??/?www.21cnjy.com?/??)师生共同归纳画函数图像的步骤:画二次函数的图像一般用描点法,分为以下三步:
(1)列表:观察y=ax2(a≠0)的表达式,选择适当的自变量x的值,并计算相应的函数值y,为了计算方便,x一般取整数.
(2)描点:在直角坐标系中描出各点;
(3)连线:用光滑的曲线顺次连结各点.观察函数图像回答问题:
(?http:?/??/?www.21cnjy.com?/??)1、二次函数的图像像什么?2、图像是否是对称图形,对称轴是什么?3、什么是图像的顶点?归纳出:二次函数y=ax2(a不等于0)的图像是一条抛物线,它关于y轴对称,顶点是坐标原点。牛刀小试在同一直角坐标系中,画出函数y=
x2
,y=2x2
的图像解:分别填表,再画出它们的图像,如图
(?http:?/??/?www.21cnjy.com?/??)2、在坐标图中找出各点坐标,然后连结各点
(?http:?/??/?www.21cnjy.com?/??)观察:函数,的图像与函数的图像相比,有什么共同点和不同点?相同点:开口都向上,顶点是原点而且是抛物线的最低点,对称轴是
y
轴不同点:a
要越大,抛物线的开口越小.在同一个坐标系中画出二次函数
和的图像。1.
列自变量y与函数x的对应值表.
(?http:?/??/?www.21cnjy.com?/??)2.
描点,
并用光滑曲线顺次连结各点,
即可得到函数与
的图像
(?http:?/??/?www.21cnjy.com?/??)想一想二次函数的图像与的图像关于什么对称?如果已知的图像,你认为可怎样更方便地得到的图像?填一填
(?http:?/??/?www.21cnjy.com?/??)归纳:二次函数的性质:二次函数y=ax2(a不等于0)的图像是一
(?http:?/??/?www.21cnjy.com?)条抛物线,它关于y轴对称,顶点是坐标原点。当a>0时,抛物线的开口向上,顶点是抛物线的最低点;当a<0时,抛物线的开口向下,顶点是抛物线的最高点。例1、已知二次函数y=ax2(a≠0)的图像经过点(-2,-3).
(1)求a的值,并写出这个二次函数的解析式.(2)说出这个二次函数的顶点坐标、对称轴、开口方向和图像的位置.例2、已知函数的图像是抛物线(1)求m的值;(2)当m为何值时,抛物线的开口向下?(3)当m为何值时,抛物线有最低点?并写出它的顶点坐标和对称轴。
学生根据函数解析式,把x值代入得出y的值,填表。在坐标系中描出点,用光滑曲线顺次连结,得出函数图像。共同归纳学生观察函数图像,回答问题学生根据前面的图像的画法,试着画出图像。学生通过解答,可以对知识进行巩固。根据问题,学生交流,思考,得出相同点和不同点。学生自主解答,老师巡视指导学生分组解答,师提问
学生填表格对函数图像的性质进行归纳
学生自主解答,教师适时的进行提示,并板书
在教法设计上引导学生自主、合作,通过函数关系式列表画出函数图像,感受归纳、类比的数学建模的过程,尝试并体验对问题的探究。增强学生观察和归纳总结的能力。再以所得的函数图像,提出、点明二次函数的图像的形状,是否对称,对称轴,顶点等一系列问题。在教学脉络上更具:连贯性、简洁性。课堂教学必须在师生、生生的互动氛围中,引导
(?http:?/??/?www.21cnjy.com?)学生从感性认识到理性认知的过渡,培养、形成抽象思维的意识和能力,从而激发学生认识活动中反思、再认识的科学态度。让学生自己动手解答问题,检验知识的掌握情况。培养学生解决问题的能力和归纳的能力通过例题的解答,使学生对知识的掌握进一步的提高。
巩固提升
1.如图所示的函数图像所表示的表达式有可能是( )
(?http:?/??/?www.21cnjy.com?/??)
A.y=-x2
B.y=x2C.y=x
D.答案:B2.下列各点在抛物线y=2x2上的是( )
A.(2,1)
B.(1,2)
C.(1,-2)
D.(-1,-2)答案:B3、已知二次函数y=的图像开口向下,则( )
A.m<-1 B.m=-1
C.m<1
D.m=1
答案:B4.关于二次函数y=x2的图像,下列说法错误的是( )
A.它的形状是一条抛物线
B.它的开口向上,且关于y轴对称
C.它的顶点是抛物线的最高点
D.它与y=-x2的图像关于x轴对称答案:C5、已知抛物线经过点A(-2,-8)。(1)求此抛物线的函数解析式;(2)判断点B(-1,-4)是否在此抛物线上。(3)求出此抛物线上纵坐标为-6的点的坐标。答案:解:(1)将点A(-2,-8)代入中,即:-8=4a∴a=-2∴抛物线的解析式为:(2)将点B(-1,-4)代入-4=-2,不成立∴点B不在抛物线上。(3)将-6代入解析式,即-6=-2解得:x=
±6、拱桥的形状是抛物线,其函数关系式为y=-x2,当水面离桥顶的高度为m时,(1)水面的宽度为多少米?
(2)有一艘货船,出水面的高度为5米,宽为6米,问此船能否安全通过桥洞?
(?http:?/??/?www.21cnjy.com?/??)答案:解:(1)在y=-x2中,
当y=-时,x=±5,
故水面的宽度为2×5=10米.
答:水面的宽度为10米.
(2)
∵货船宽为6米∴当x=-3,x=3时,y=∵5>3∴此船能安全通过桥洞。
学生自主解答,教师讲解答案。
鼓励
(?http:?/??/?www.21cnjy.com?)学生认真思考;发现解决问题的方法,引导学生主动地参与教学活动,发扬数学民主,让学生在独立思考、合作交流等数学活动中,培养学生合作互助意识,提高数学交流与数学表达能力。
课堂小结
1.画二次函数的图像一般用描点法,分为以下三步:
(1)列表:观察y=ax2(a≠0)的表达式,选择适当的自变量x的值,并计算相应的函数值y,为了计算方便,x一般取整数.
(2)描点:在直角坐标系中描出各点;
(3)连线:用光滑的曲线顺次连结各点.2.二次函数的性质:二次函数y=ax2(a不等于0)的图像
(?http:?/??/?www.21cnjy.com?)是一条抛物线,它关于y轴对称,顶点是坐标原点。当a>0时,抛物线的开口向上,顶点是抛物线的最低点;当a<0时,抛物线的开口向下,顶点是抛物线的最高点。
学生归纳本节所学知识
培养学生总结,归纳的能力。
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
同课章节目录
