2021-2022学年浙教版九年级上第2章 简单事件的概率单元测试一(含解析)
文档属性
| 名称 | 2021-2022学年浙教版九年级上第2章 简单事件的概率单元测试一(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-29 14:37:24 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版九年级上第2章
简单事件的概率单元测试(1)
一.选择题(共12小题,每小题3分,共36分)
1.(2021?江川区模拟)一只不透明的袋子里装有4个黑球,2个白球,每个球除颜色外都相同,则事件“从中任意摸出3个球,至少有1个球是黑球”的事件类型是( )
A.随机事件
B.不可能事件
C.必然事件
D.无法确定
2.(2020秋?甘井子区期末)下列事件中,属于必然事件的是( )
A.明天的最高气温将达35℃
B.任意购买一张动车票,座位刚好挨着窗口
C.掷两次质地均匀的骰子,其中有一次正面朝上
D.对顶角相等
3.(2021?烟台)连接正六边形不相邻的两个顶点,并将中间的六边形涂成黑色,制成如图所示的镖盘,将一枚飞镖任意投掷到镖盘上,飞镖落在黑色区域的概率为( )
A.
B.
C.
D.
4.(2020秋?河东区期末)抛掷一枚质地均匀的硬币,“反面朝上”的概率为,那么抛掷一枚质地均匀的硬币100次,下列理解正确的是( )
A.每两次必有1次反面朝上
B.可能有50次反面朝上
C.必有50次反面朝上
D.不可能有100次反面朝上
5.(2021春?皇姑区期末)如图,在边长为1的小正方形网格中,已知AB在网格格点上,在所有的16个格点中任选一点C,恰好能使点A,B,C构成面积为1的三角形的概率是( )
A.
B.
C.
D.
6.(2020?汉阳区校级模拟)某超市为了吸引顾客,设计了一种返现促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样,规定:顾客在本超市一次性消费满200元,就可以在箱子里一次性摸出两个小球,两球数字之和记为返现金额.某顾客刚好消费200元,则该顾客所获得返现金额低于30元的概率是( )
A.
B.
C.
D.
7.(2021?三水区一模)甲袋中装有2张相同的卡片,颜色分别为红色和黄色;乙袋中装有3张相同的卡片,颜色分别为红色、黄色、绿色.从这两个口袋中各随机抽取1张卡片,取出的两张卡片中至少有一张是红色的概率是( )
A.
B.
C.
D.
8.(2020秋?昌图县期末)若从1,2,3,4四个数中选取一个数,记为a,再从这四个数中选取一个数,记为c,则关于x的一元二次方程ax2+4x+c=0没有实数根的概率为( )
A.
B.
C.
D.
9.(2020秋?重庆期末)一个不透明的袋子中装有3个白球,2个黑球,它们除了颜色外都相同.将球摇匀后,从中随机摸出一个球,记下颜色后放回,再随机摸出一个球.两次摸到的球颜色相同的概率是( )
A.
B.
C.
D.
10.(2021?武汉模拟)小张和小王相约去参加“抗疫情党员志愿者进社区服务”活动现在有A、B、C三个社区可供随机选择,他们两人恰好进入同一社区的概率是( )
A.
B.
C.
D.
11.(2020?山西模拟)在不透明的甲口袋中装有32个红球和8个黑球,在不透明的乙口袋中装有48个红球,20个黑球和32个白球.这些球除了颜色外没有其他区别.搅匀两口袋中的球,从口袋中分别任意摸出一个球,下列说法正确的是( )
A.从甲口袋中摸到黑球的概率较大
B.从乙口袋中摸到黑球的概率较大
C.从甲、乙两口袋中摸到黑球的概率相等
D.无法比较从甲、乙两口袋中摸到黑球的概率
12.(2021?新华区模拟)某市公园的东、南、西、北方向上各有一个入口,周末佳佳和琪琪随机从一个入口进入该公园游玩,则佳佳和琪琪恰好从同一个入口进入该公园的概率是( )
A.
B.
C.
D.
二.填空题(共7小题,每小题4分,共28分)
13.(2020秋?五峰县期末)在一个箱子里放有2个白球和5个红球,现摸出1个球是黑球,这个事件属于
事件.(填“必然、不确定或不可能”)
14.(2020秋?天河区期末)在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数可能是
个.
15.(2020秋?鄄城县期末)在一个不透明的袋子中装有6个白球和若干个红球,这些球除颜色外都相同.每次从袋子中随机摸出一个球,记下颜色后再放回袋中,通过多次重复试验发现摸出白球的频率稳定在0.3附近,则估计袋子中的红球有
个.
16.(2021?津南区模拟)在一个不透明的袋子中只装有n个白球和4个红球,这些球除颜色外其他均相同.如果从袋子中随机摸出一个球,摸到红球的概率是,那么n的值为
.
17.(2021?沙坪坝区校级模拟)不透明的袋子里装有除标号外完全一样的四个小球,小球上分别标有﹣5,﹣1,2,3这四个数字,从袋子中随机抽取一个小球,记标号为m,不放回后将袋子摇匀,再随机抽取一个小球,记标号为n,则m,n使得二次函数y=mx2+n的图象同时经过四个象限的概率为
.
18.(2021?嘉兴)看了《田忌赛马》故事后,小杨用数学模型来分析:齐王与田忌的上中下三个等级的三匹马记分如表,每匹马只赛一场,两数相比,大数为胜,三场两胜则赢.已知齐王的三匹马出场顺序为10,8,6.若田忌的三匹马随机出场,则田忌能赢得比赛的概率为
.
马匹姓名
下等马
中等马
上等马
齐王
6
8
10
田忌
5
7
9
19.(2021?长沙模拟)为了防止输入性“新冠肺炎”,某医院成立隔离治疗发热病人防控小组,决定从内科3位骨干医师中(含有甲)抽调2人组成.则甲一定会被抽调到防控小组的概率是
.
三.解答题(共5小题,共56分)
20.(10分)(2021?萧山区二模)文具店购进了20盒“2B”铅笔,但在销售过程中,发现其中混入了若干“HB”铅笔.店员进行统计后,发现每盒铅笔中最多混入了2支“HB”铅笔,具体数据见下表:
混入“HB”铅笔数
0
1
2
盒数
6
m
n
(1)用等式写出m,n所满足的数量关系
;
(2)从20盒铅笔中任意选取1盒:
①“盒中没有混入‘HB’铅笔”是
事件(填“必然”、“不可能”或“随机”);
②若“盒中混入1支‘HB’铅笔”的概率为,求m和n的值.
21.(10分)(2018?贵阳模拟)如图,在3×3的方格纸中,点A,B,C,D,E分别位于格点上.
(1)从A,D,E三点中任意取一点,以所取的这一点及B,C为顶点画三角形,则所画三角形是直角三角形的概率是
;
(2)从A,D,E三点中先后任意取两个不同的点,以所取的这两点及B,C为顶点画四边形,求所画四边形是平行四边形的概率(用树状图列表的方法求解)
22.(12分)(2021?常州一模)如图,将等边三角形、圆、平行四边形这三种图形分别画在3张大小、质地均相同的正方形小纸板上,将这3张正方形小纸板放入一只不透明的袋子中.
(1)搅匀后从中摸出一张小纸板,摸出的纸板上的图形是中心对称图形的概率是
;
(2)搅匀后从中摸出一张小纸板,记下纸板上图形的名称后放回袋子中,再从中摸出一张小纸板,求两次摸出的小纸板上的图形都是轴对称图形的概率.
23.(12分)(2021春?无锡期中)一个不透明的口袋中放着若干个红球和黑球,这两种球除了颜色之外没有其他任何区别,袋中的球已经搅匀,闭眼从口袋中摸出一个球,经过很多次实验发现摸到红球的频率逐渐稳定在.
(1)估计摸到黑球的概率是
;
(2)如果袋中原有红球12个,又放入n个黑球,再经过很多次实验发现摸到黑球的频率逐渐稳定在,求n的值.
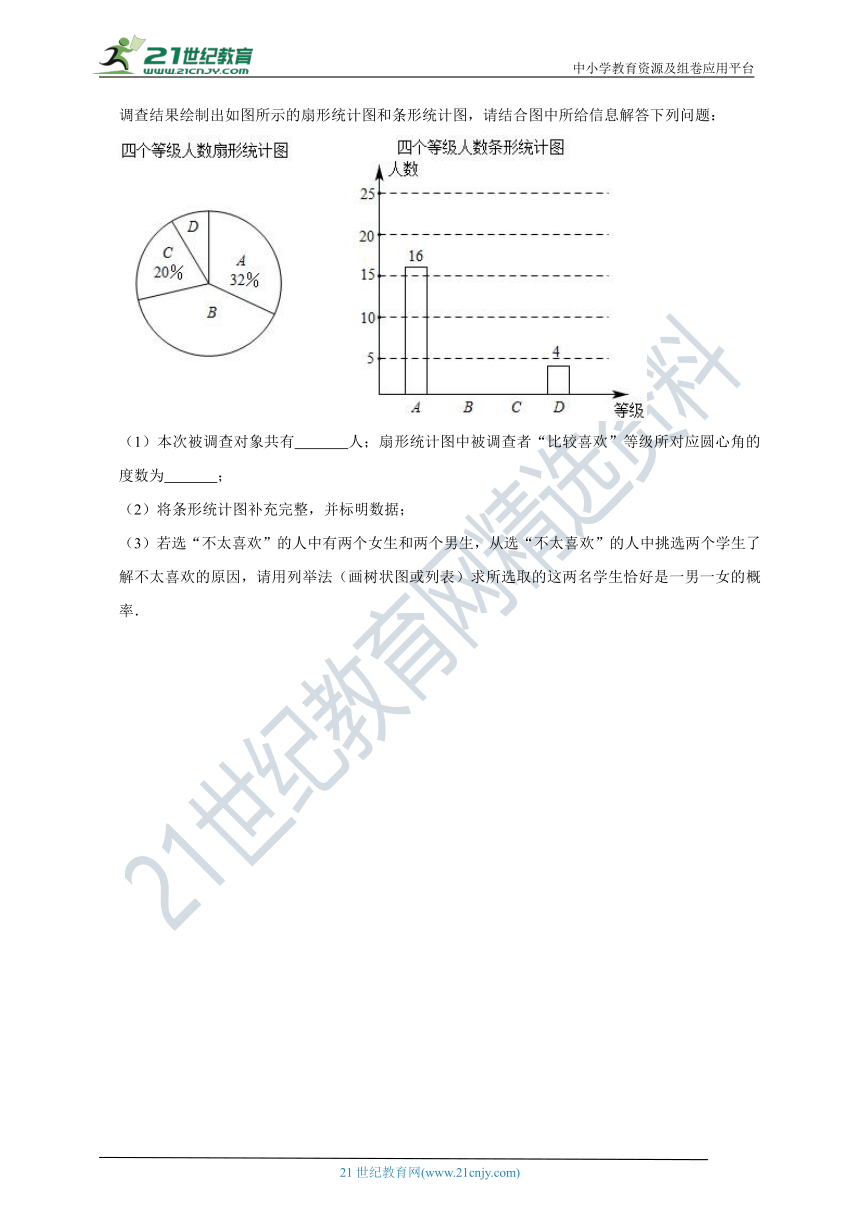
24.(12分)(2021?滨城区一模)2021年上映的《你好,李焕英》票房破50亿,某中学就《你好,李焕英》电影的喜爱程度,在校内对部分学生进行了问卷调查,并对问卷调查的结果分为“非常喜欢”、“比较喜欢”、“感觉一般”、“不太喜欢”四个等级,分别记作A、B、C、D.根据调查结果绘制出如图所示的扇形统计图和条形统计图,请结合图中所给信息解答下列问题:
(1)本次被调查对象共有
人;扇形统计图中被调查者“比较喜欢”等级所对应圆心角的度数为
;
(2)将条形统计图补充完整,并标明数据;
(3)若选“不太喜欢”的人中有两个女生和两个男生,从选“不太喜欢”的人中挑选两个学生了解不太喜欢的原因,请用列举法(画树状图或列表)求所选取的这两名学生恰好是一男一女的概率.
答案与解析
一.选择题
1.(2021?江川区模拟)一只不透明的袋子里装有4个黑球,2个白球,每个球除颜色外都相同,则事件“从中任意摸出3个球,至少有1个球是黑球”的事件类型是( )
A.随机事件
B.不可能事件
C.必然事件
D.无法确定
【解析】解:∵一只不透明的袋子里装有4个黑球,2个白球,每个球除颜色外都相同,
∴事件“从中任意摸出3个球,至少有1个球是黑球”的事件类型是必然事件.
故选:C.
2.(2020秋?甘井子区期末)下列事件中,属于必然事件的是( )
A.明天的最高气温将达35℃
B.任意购买一张动车票,座位刚好挨着窗口
C.掷两次质地均匀的骰子,其中有一次正面朝上
D.对顶角相等
【解析】解:“对顶角相等”是真命题,发生的可能性为100%,
故选:D.
3.(2021?烟台)连接正六边形不相邻的两个顶点,并将中间的六边形涂成黑色,制成如图所示的镖盘,将一枚飞镖任意投掷到镖盘上,飞镖落在黑色区域的概率为( )
A.
B.
C.
D.
【解析】解:如图所示,令S△ABC=a,
则S阴影=6a,S正六边形=18a,
∴将一枚飞镖任意投掷到镖盘上,飞镖落在黑色区域的概率为=,
故选:B.
4.(2020秋?河东区期末)抛掷一枚质地均匀的硬币,“反面朝上”的概率为,那么抛掷一枚质地均匀的硬币100次,下列理解正确的是( )
A.每两次必有1次反面朝上
B.可能有50次反面朝上
C.必有50次反面朝上
D.不可能有100次反面朝上
【解析】解:抛掷一枚质地均匀的硬币,“反面朝上”的概率为,那么抛掷一枚质地均匀的硬币100次,可能有50次反面朝上,
故选:B.
5.(2021春?皇姑区期末)如图,在边长为1的小正方形网格中,已知AB在网格格点上,在所有的16个格点中任选一点C,恰好能使点A,B,C构成面积为1的三角形的概率是( )
A.
B.
C.
D.
【解析】解:∵在格点中任意放置点C,共有16种等可能的结果,恰好能使△ABC的面积为1的有4种情况,
∴恰好能使△ABC的面积为1的概率为:=.
故选:C.
6.(2020?汉阳区校级模拟)某超市为了吸引顾客,设计了一种返现促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样,规定:顾客在本超市一次性消费满200元,就可以在箱子里一次性摸出两个小球,两球数字之和记为返现金额.某顾客刚好消费200元,则该顾客所获得返现金额低于30元的概率是( )
A.
B.
C.
D.
【解析】解:用列表法表示所有可能出现的结果如下:
共有12种等可能出现的结果,其中少于30元的有4种,
∴该顾客所获得返现金额低于30元的概率是=,
故选:D.
7.(2021?三水区一模)甲袋中装有2张相同的卡片,颜色分别为红色和黄色;乙袋中装有3张相同的卡片,颜色分别为红色、黄色、绿色.从这两个口袋中各随机抽取1张卡片,取出的两张卡片中至少有一张是红色的概率是( )
A.
B.
C.
D.
【解析】解:画树状图如图:
共有6个等可能的结果,取出的两张卡片中至少有一张是红色的结果有4个,
∴取出的两张卡片中至少有一张是红色的概率为=,
故选:A.
8.(2020秋?昌图县期末)若从1,2,3,4四个数中选取一个数,记为a,再从这四个数中选取一个数,记为c,则关于x的一元二次方程ax2+4x+c=0没有实数根的概率为( )
A.
B.
C.
D.
【解析】解:画树状图如图:
由树形图可知:共有16种等可能的结果,其中使42﹣4ac<0的有8种结果,
∴关于x的一元二次方程ax2+4x+c=0没有实数根的概率为=,
故选:C.
9.(2020秋?重庆期末)一个不透明的袋子中装有3个白球,2个黑球,它们除了颜色外都相同.将球摇匀后,从中随机摸出一个球,记下颜色后放回,再随机摸出一个球.两次摸到的球颜色相同的概率是( )
A.
B.
C.
D.
【解析】解:画树状图如图:
共有25种等可能的结果,两次摸出的球颜色相同有13种情况,
∴两次摸出的球颜色相同的概率为,
故选:B.
10.(2021?武汉模拟)小张和小王相约去参加“抗疫情党员志愿者进社区服务”活动现在有A、B、C三个社区可供随机选择,他们两人恰好进入同一社区的概率是( )
A.
B.
C.
D.
【解析】解:画树状图如图:
共有9种等可能的结果数,其中两人恰好选择同一社区的结果为3种,
则两人恰好进入同一社区的概率==.
故选:B.
11.(2020?山西模拟)在不透明的甲口袋中装有32个红球和8个黑球,在不透明的乙口袋中装有48个红球,20个黑球和32个白球.这些球除了颜色外没有其他区别.搅匀两口袋中的球,从口袋中分别任意摸出一个球,下列说法正确的是( )
A.从甲口袋中摸到黑球的概率较大
B.从乙口袋中摸到黑球的概率较大
C.从甲、乙两口袋中摸到黑球的概率相等
D.无法比较从甲、乙两口袋中摸到黑球的概率
【解析】解:∵甲口袋中装有32个红球和8个黑球,
球的总个数为:32+8=40个;
黑球的个数为:8个,
∵乙口袋中装有48个红球,20个黑球和32个白球,
球的总个数为:48+20+32=100个,
黑球的个数为:20个,
∴从甲口袋摸到黑球的概率==;
从乙口袋摸到黑球的概率==
∴从甲、乙两口袋中摸到黑球的概率相等,
故选:C.
12.(2021?新华区模拟)某市公园的东、南、西、北方向上各有一个入口,周末佳佳和琪琪随机从一个入口进入该公园游玩,则佳佳和琪琪恰好从同一个入口进入该公园的概率是( )
A.
B.
C.
D.
【解析】解:画树状图如下:
由树状图可知,共有16种等可能结果,其中佳佳和琪琪恰好从同一个入口进入该公园的有4种等可能结果,
所以佳佳和琪琪恰好从同一个入口进入该公园的概率为=,
故选:B.
二.填空题
13.(2020秋?五峰县期末)在一个箱子里放有2个白球和5个红球,现摸出1个球是黑球,这个事件属于 不可能 事件.(填“必然、不确定或不可能”)
【解析】解:在一个箱子里放有2个白球和5个红球,现摸出1个球是黑球,这个事件属于不可能事件,
故答案为:不可能.
14.(2020秋?天河区期末)在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数可能是 5 个.
【解析】解:设袋子中红球有x个,
根据题意,得:=0.25,
解得x=5,
即袋子中红球的个数可能是5个,
故答案为:5.
15.(2020秋?鄄城县期末)在一个不透明的袋子中装有6个白球和若干个红球,这些球除颜色外都相同.每次从袋子中随机摸出一个球,记下颜色后再放回袋中,通过多次重复试验发现摸出白球的频率稳定在0.3附近,则估计袋子中的红球有 14 个.
【解析】解:∵通过多次重复试验发现摸出白球的频率稳定在0.3附近,
∴从袋子中任意摸出1个球,是白球的概率约为0.3,
设袋子中红球有x个,
根据题意,得:=0.3,
解得x=14,
经检验:x=14是分式方程的解,
∴估计袋子中的红球有14个,
故答案为:14.
16.(2021?津南区模拟)在一个不透明的袋子中只装有n个白球和4个红球,这些球除颜色外其他均相同.如果从袋子中随机摸出一个球,摸到红球的概率是,那么n的值为 8 .
【解析】解:根据题意得,
解得n=8,
经检验:n=48是分式方程的解,
故答案为:8.
17.(2021?沙坪坝区校级模拟)不透明的袋子里装有除标号外完全一样的四个小球,小球上分别标有﹣5,﹣1,2,3这四个数字,从袋子中随机抽取一个小球,记标号为m,不放回后将袋子摇匀,再随机抽取一个小球,记标号为n,则m,n使得二次函数y=mx2+n的图象同时经过四个象限的概率为 .
【解析】解:画树状图如图:
共有12个等可能的结果,m,n使得二次函数y=mx2+n的图象同时经过四个象限的结果有8个,
∴m,n使得二次函数y=mx2+n的图象同时经过四个象限的概率为=,
故答案为:.
18.(2021?嘉兴)看了《田忌赛马》故事后,小杨用数学模型来分析:齐王与田忌的上中下三个等级的三匹马记分如表,每匹马只赛一场,两数相比,大数为胜,三场两胜则赢.已知齐王的三匹马出场顺序为10,8,6.若田忌的三匹马随机出场,则田忌能赢得比赛的概率为
.
马匹姓名
下等马
中等马
上等马
齐王
6
8
10
田忌
5
7
9
【解析】解:由于田忌的上、中等马分别比齐王的中、下等马强,当齐王的三匹马出场顺序为10,8,6时,田忌的马按5,9,7的顺序出场,田忌才能赢得比赛,
当田忌的三匹马随机出场时,双方马的对阵情况如下:
双方马的对阵中,只有一种对阵情况田忌能赢,
∴田忌能赢得比赛的概率为.
故答案为:.
19.(2021?长沙模拟)为了防止输入性“新冠肺炎”,某医院成立隔离治疗发热病人防控小组,决定从内科3位骨干医师中(含有甲)抽调2人组成.则甲一定会被抽调到防控小组的概率是 .
【解析】解:内科3位骨干医师分别即为甲、乙、丙,
画树状图如图:
共有6个等可能的结果,甲一定会被抽调到防控小组的结果有4个,
∴甲一定会被抽调到防控小组的概率==;
故答案为:.
三.解答题
20.(2021?萧山区二模)文具店购进了20盒“2B”铅笔,但在销售过程中,发现其中混入了若干“HB”铅笔.店员进行统计后,发现每盒铅笔中最多混入了2支“HB”铅笔,具体数据见下表:
混入“HB”铅笔数
0
1
2
盒数
6
m
n
(1)用等式写出m,n所满足的数量关系 m+n=14 ;
(2)从20盒铅笔中任意选取1盒:
①“盒中没有混入‘HB’铅笔”是 随机 事件(填“必然”、“不可能”或“随机”);
②若“盒中混入1支‘HB’铅笔”的概率为,求m和n的值.
【解析】解:(1)观察表格发现:6+m+n=20,
∴用等式写出m,n所满足的数量关系为m+n=14,
故答案为:m+n=14;
(2)①“盒中没有混入‘HB’铅笔”是随机事件,
故答案为:随机;
②∵“盒中混入1支‘HB’铅笔”的概率为,
∴=,
∴m=5,n=9.
21.(2018?贵阳模拟)如图,在3×3的方格纸中,点A,B,C,D,E分别位于格点上.
(1)从A,D,E三点中任意取一点,以所取的这一点及B,C为顶点画三角形,则所画三角形是直角三角形的概率是 ;
(2)从A,D,E三点中先后任意取两个不同的点,以所取的这两点及B,C为顶点画四边形,求所画四边形是平行四边形的概率(用树状图列表的方法求解)
【解析】解:(1)以所取的这一点及B,C为顶点画三角形有△ABC、△DBC、△EBC三种情况,
其中所画三角形是直角三角形的有△ABC、△DBC这2种结果,
所以所画三角形是直角三角形的概率是,
故答案为:;
(2)画树状图如下:
由树状图可知共有6种等可能结果,其中与以B、C为顶点所画四边形是平行四边形的有2种结果,
∴所画四边形是平行四边形的概率为=.
22.(2021?常州一模)如图,将等边三角形、圆、平行四边形这三种图形分别画在3张大小、质地均相同的正方形小纸板上,将这3张正方形小纸板放入一只不透明的袋子中.
(1)搅匀后从中摸出一张小纸板,摸出的纸板上的图形是中心对称图形的概率是 ;
(2)搅匀后从中摸出一张小纸板,记下纸板上图形的名称后放回袋子中,再从中摸出一张小纸板,求两次摸出的小纸板上的图形都是轴对称图形的概率.
【解析】解:(1)等边三角形是轴对称图形,圆既是轴对称图形也是中心对称图形,平行四边形是中心对称图形,
则摸出的纸板上的图形是中心对称图形的概率是,
故答案为:;
(2)把画有等边三角形、圆、平行四边形的正方形小纸板上分别记为A、B、C,画树状图如图:
共有9个等可能的结果,两次摸出的小纸板上的图形都是轴对称图形的结果有4个,
∴两次摸出的小纸板上的图形都是轴对称图形的概率为.
23.(2021春?无锡期中)一个不透明的口袋中放着若干个红球和黑球,这两种球除了颜色之外没有其他任何区别,袋中的球已经搅匀,闭眼从口袋中摸出一个球,经过很多次实验发现摸到红球的频率逐渐稳定在.
(1)估计摸到黑球的概率是 ;
(2)如果袋中原有红球12个,又放入n个黑球,再经过很多次实验发现摸到黑球的频率逐渐稳定在,求n的值.
【解析】解:(1)P(取出黑球)=1﹣P(取出红球)=1﹣=;
故答案为:;
(2)设袋子中原有黑球x个,
根据题意得:=,
解得:x=18,
经检验x=18是原方程的根,
所以黑球有18个,
∵又放入了n个黑球,
根据题意得:=,
解得:n=6.
24.(2021?滨城区一模)2021年上映的《你好,李焕英》票房破50亿,某中学就《你好,李焕英》电影的喜爱程度,在校内对部分学生进行了问卷调查,并对问卷调查的结果分为“非常喜欢”、“比较喜欢”、“感觉一般”、“不太喜欢”四个等级,分别记作A、B、C、D.根据调查结果绘制出如图所示的扇形统计图和条形统计图,请结合图中所给信息解答下列问题:
(1)本次被调查对象共有 50 人;扇形统计图中被调查者“比较喜欢”等级所对应圆心角的度数为 144° ;
(2)将条形统计图补充完整,并标明数据;
(3)若选“不太喜欢”的人中有两个女生和两个男生,从选“不太喜欢”的人中挑选两个学生了解不太喜欢的原因,请用列举法(画树状图或列表)求所选取的这两名学生恰好是一男一女的概率.
【解析】解:(1)本次被调查对象共有:16÷32%=50(人),
被调查者“比较喜欢”有:50﹣16﹣4﹣50×20%=20(人);
则扇形统计图中被调查者“比较喜欢”等级所对应圆心角的度数为360°×=144°
故答案为:50,144°;
(2)C等级的人数有:50﹣16﹣20﹣4=10(人),
将条形统计图补充完整如下:
(3)画树状图如图:
共有12个等可能的结果,所选取的这两名学生恰好是一男一女的结果有8个,
∴所选取的这两名学生恰好是一男一女的概率为=.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
浙教版九年级上第2章
简单事件的概率单元测试(1)
一.选择题(共12小题,每小题3分,共36分)
1.(2021?江川区模拟)一只不透明的袋子里装有4个黑球,2个白球,每个球除颜色外都相同,则事件“从中任意摸出3个球,至少有1个球是黑球”的事件类型是( )
A.随机事件
B.不可能事件
C.必然事件
D.无法确定
2.(2020秋?甘井子区期末)下列事件中,属于必然事件的是( )
A.明天的最高气温将达35℃
B.任意购买一张动车票,座位刚好挨着窗口
C.掷两次质地均匀的骰子,其中有一次正面朝上
D.对顶角相等
3.(2021?烟台)连接正六边形不相邻的两个顶点,并将中间的六边形涂成黑色,制成如图所示的镖盘,将一枚飞镖任意投掷到镖盘上,飞镖落在黑色区域的概率为( )
A.
B.
C.
D.
4.(2020秋?河东区期末)抛掷一枚质地均匀的硬币,“反面朝上”的概率为,那么抛掷一枚质地均匀的硬币100次,下列理解正确的是( )
A.每两次必有1次反面朝上
B.可能有50次反面朝上
C.必有50次反面朝上
D.不可能有100次反面朝上
5.(2021春?皇姑区期末)如图,在边长为1的小正方形网格中,已知AB在网格格点上,在所有的16个格点中任选一点C,恰好能使点A,B,C构成面积为1的三角形的概率是( )
A.
B.
C.
D.
6.(2020?汉阳区校级模拟)某超市为了吸引顾客,设计了一种返现促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样,规定:顾客在本超市一次性消费满200元,就可以在箱子里一次性摸出两个小球,两球数字之和记为返现金额.某顾客刚好消费200元,则该顾客所获得返现金额低于30元的概率是( )
A.
B.
C.
D.
7.(2021?三水区一模)甲袋中装有2张相同的卡片,颜色分别为红色和黄色;乙袋中装有3张相同的卡片,颜色分别为红色、黄色、绿色.从这两个口袋中各随机抽取1张卡片,取出的两张卡片中至少有一张是红色的概率是( )
A.
B.
C.
D.
8.(2020秋?昌图县期末)若从1,2,3,4四个数中选取一个数,记为a,再从这四个数中选取一个数,记为c,则关于x的一元二次方程ax2+4x+c=0没有实数根的概率为( )
A.
B.
C.
D.
9.(2020秋?重庆期末)一个不透明的袋子中装有3个白球,2个黑球,它们除了颜色外都相同.将球摇匀后,从中随机摸出一个球,记下颜色后放回,再随机摸出一个球.两次摸到的球颜色相同的概率是( )
A.
B.
C.
D.
10.(2021?武汉模拟)小张和小王相约去参加“抗疫情党员志愿者进社区服务”活动现在有A、B、C三个社区可供随机选择,他们两人恰好进入同一社区的概率是( )
A.
B.
C.
D.
11.(2020?山西模拟)在不透明的甲口袋中装有32个红球和8个黑球,在不透明的乙口袋中装有48个红球,20个黑球和32个白球.这些球除了颜色外没有其他区别.搅匀两口袋中的球,从口袋中分别任意摸出一个球,下列说法正确的是( )
A.从甲口袋中摸到黑球的概率较大
B.从乙口袋中摸到黑球的概率较大
C.从甲、乙两口袋中摸到黑球的概率相等
D.无法比较从甲、乙两口袋中摸到黑球的概率
12.(2021?新华区模拟)某市公园的东、南、西、北方向上各有一个入口,周末佳佳和琪琪随机从一个入口进入该公园游玩,则佳佳和琪琪恰好从同一个入口进入该公园的概率是( )
A.
B.
C.
D.
二.填空题(共7小题,每小题4分,共28分)
13.(2020秋?五峰县期末)在一个箱子里放有2个白球和5个红球,现摸出1个球是黑球,这个事件属于
事件.(填“必然、不确定或不可能”)
14.(2020秋?天河区期末)在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数可能是
个.
15.(2020秋?鄄城县期末)在一个不透明的袋子中装有6个白球和若干个红球,这些球除颜色外都相同.每次从袋子中随机摸出一个球,记下颜色后再放回袋中,通过多次重复试验发现摸出白球的频率稳定在0.3附近,则估计袋子中的红球有
个.
16.(2021?津南区模拟)在一个不透明的袋子中只装有n个白球和4个红球,这些球除颜色外其他均相同.如果从袋子中随机摸出一个球,摸到红球的概率是,那么n的值为
.
17.(2021?沙坪坝区校级模拟)不透明的袋子里装有除标号外完全一样的四个小球,小球上分别标有﹣5,﹣1,2,3这四个数字,从袋子中随机抽取一个小球,记标号为m,不放回后将袋子摇匀,再随机抽取一个小球,记标号为n,则m,n使得二次函数y=mx2+n的图象同时经过四个象限的概率为
.
18.(2021?嘉兴)看了《田忌赛马》故事后,小杨用数学模型来分析:齐王与田忌的上中下三个等级的三匹马记分如表,每匹马只赛一场,两数相比,大数为胜,三场两胜则赢.已知齐王的三匹马出场顺序为10,8,6.若田忌的三匹马随机出场,则田忌能赢得比赛的概率为
.
马匹姓名
下等马
中等马
上等马
齐王
6
8
10
田忌
5
7
9
19.(2021?长沙模拟)为了防止输入性“新冠肺炎”,某医院成立隔离治疗发热病人防控小组,决定从内科3位骨干医师中(含有甲)抽调2人组成.则甲一定会被抽调到防控小组的概率是
.
三.解答题(共5小题,共56分)
20.(10分)(2021?萧山区二模)文具店购进了20盒“2B”铅笔,但在销售过程中,发现其中混入了若干“HB”铅笔.店员进行统计后,发现每盒铅笔中最多混入了2支“HB”铅笔,具体数据见下表:
混入“HB”铅笔数
0
1
2
盒数
6
m
n
(1)用等式写出m,n所满足的数量关系
;
(2)从20盒铅笔中任意选取1盒:
①“盒中没有混入‘HB’铅笔”是
事件(填“必然”、“不可能”或“随机”);
②若“盒中混入1支‘HB’铅笔”的概率为,求m和n的值.
21.(10分)(2018?贵阳模拟)如图,在3×3的方格纸中,点A,B,C,D,E分别位于格点上.
(1)从A,D,E三点中任意取一点,以所取的这一点及B,C为顶点画三角形,则所画三角形是直角三角形的概率是
;
(2)从A,D,E三点中先后任意取两个不同的点,以所取的这两点及B,C为顶点画四边形,求所画四边形是平行四边形的概率(用树状图列表的方法求解)
22.(12分)(2021?常州一模)如图,将等边三角形、圆、平行四边形这三种图形分别画在3张大小、质地均相同的正方形小纸板上,将这3张正方形小纸板放入一只不透明的袋子中.
(1)搅匀后从中摸出一张小纸板,摸出的纸板上的图形是中心对称图形的概率是
;
(2)搅匀后从中摸出一张小纸板,记下纸板上图形的名称后放回袋子中,再从中摸出一张小纸板,求两次摸出的小纸板上的图形都是轴对称图形的概率.
23.(12分)(2021春?无锡期中)一个不透明的口袋中放着若干个红球和黑球,这两种球除了颜色之外没有其他任何区别,袋中的球已经搅匀,闭眼从口袋中摸出一个球,经过很多次实验发现摸到红球的频率逐渐稳定在.
(1)估计摸到黑球的概率是
;
(2)如果袋中原有红球12个,又放入n个黑球,再经过很多次实验发现摸到黑球的频率逐渐稳定在,求n的值.
24.(12分)(2021?滨城区一模)2021年上映的《你好,李焕英》票房破50亿,某中学就《你好,李焕英》电影的喜爱程度,在校内对部分学生进行了问卷调查,并对问卷调查的结果分为“非常喜欢”、“比较喜欢”、“感觉一般”、“不太喜欢”四个等级,分别记作A、B、C、D.根据调查结果绘制出如图所示的扇形统计图和条形统计图,请结合图中所给信息解答下列问题:
(1)本次被调查对象共有
人;扇形统计图中被调查者“比较喜欢”等级所对应圆心角的度数为
;
(2)将条形统计图补充完整,并标明数据;
(3)若选“不太喜欢”的人中有两个女生和两个男生,从选“不太喜欢”的人中挑选两个学生了解不太喜欢的原因,请用列举法(画树状图或列表)求所选取的这两名学生恰好是一男一女的概率.
答案与解析
一.选择题
1.(2021?江川区模拟)一只不透明的袋子里装有4个黑球,2个白球,每个球除颜色外都相同,则事件“从中任意摸出3个球,至少有1个球是黑球”的事件类型是( )
A.随机事件
B.不可能事件
C.必然事件
D.无法确定
【解析】解:∵一只不透明的袋子里装有4个黑球,2个白球,每个球除颜色外都相同,
∴事件“从中任意摸出3个球,至少有1个球是黑球”的事件类型是必然事件.
故选:C.
2.(2020秋?甘井子区期末)下列事件中,属于必然事件的是( )
A.明天的最高气温将达35℃
B.任意购买一张动车票,座位刚好挨着窗口
C.掷两次质地均匀的骰子,其中有一次正面朝上
D.对顶角相等
【解析】解:“对顶角相等”是真命题,发生的可能性为100%,
故选:D.
3.(2021?烟台)连接正六边形不相邻的两个顶点,并将中间的六边形涂成黑色,制成如图所示的镖盘,将一枚飞镖任意投掷到镖盘上,飞镖落在黑色区域的概率为( )
A.
B.
C.
D.
【解析】解:如图所示,令S△ABC=a,
则S阴影=6a,S正六边形=18a,
∴将一枚飞镖任意投掷到镖盘上,飞镖落在黑色区域的概率为=,
故选:B.
4.(2020秋?河东区期末)抛掷一枚质地均匀的硬币,“反面朝上”的概率为,那么抛掷一枚质地均匀的硬币100次,下列理解正确的是( )
A.每两次必有1次反面朝上
B.可能有50次反面朝上
C.必有50次反面朝上
D.不可能有100次反面朝上
【解析】解:抛掷一枚质地均匀的硬币,“反面朝上”的概率为,那么抛掷一枚质地均匀的硬币100次,可能有50次反面朝上,
故选:B.
5.(2021春?皇姑区期末)如图,在边长为1的小正方形网格中,已知AB在网格格点上,在所有的16个格点中任选一点C,恰好能使点A,B,C构成面积为1的三角形的概率是( )
A.
B.
C.
D.
【解析】解:∵在格点中任意放置点C,共有16种等可能的结果,恰好能使△ABC的面积为1的有4种情况,
∴恰好能使△ABC的面积为1的概率为:=.
故选:C.
6.(2020?汉阳区校级模拟)某超市为了吸引顾客,设计了一种返现促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样,规定:顾客在本超市一次性消费满200元,就可以在箱子里一次性摸出两个小球,两球数字之和记为返现金额.某顾客刚好消费200元,则该顾客所获得返现金额低于30元的概率是( )
A.
B.
C.
D.
【解析】解:用列表法表示所有可能出现的结果如下:
共有12种等可能出现的结果,其中少于30元的有4种,
∴该顾客所获得返现金额低于30元的概率是=,
故选:D.
7.(2021?三水区一模)甲袋中装有2张相同的卡片,颜色分别为红色和黄色;乙袋中装有3张相同的卡片,颜色分别为红色、黄色、绿色.从这两个口袋中各随机抽取1张卡片,取出的两张卡片中至少有一张是红色的概率是( )
A.
B.
C.
D.
【解析】解:画树状图如图:
共有6个等可能的结果,取出的两张卡片中至少有一张是红色的结果有4个,
∴取出的两张卡片中至少有一张是红色的概率为=,
故选:A.
8.(2020秋?昌图县期末)若从1,2,3,4四个数中选取一个数,记为a,再从这四个数中选取一个数,记为c,则关于x的一元二次方程ax2+4x+c=0没有实数根的概率为( )
A.
B.
C.
D.
【解析】解:画树状图如图:
由树形图可知:共有16种等可能的结果,其中使42﹣4ac<0的有8种结果,
∴关于x的一元二次方程ax2+4x+c=0没有实数根的概率为=,
故选:C.
9.(2020秋?重庆期末)一个不透明的袋子中装有3个白球,2个黑球,它们除了颜色外都相同.将球摇匀后,从中随机摸出一个球,记下颜色后放回,再随机摸出一个球.两次摸到的球颜色相同的概率是( )
A.
B.
C.
D.
【解析】解:画树状图如图:
共有25种等可能的结果,两次摸出的球颜色相同有13种情况,
∴两次摸出的球颜色相同的概率为,
故选:B.
10.(2021?武汉模拟)小张和小王相约去参加“抗疫情党员志愿者进社区服务”活动现在有A、B、C三个社区可供随机选择,他们两人恰好进入同一社区的概率是( )
A.
B.
C.
D.
【解析】解:画树状图如图:
共有9种等可能的结果数,其中两人恰好选择同一社区的结果为3种,
则两人恰好进入同一社区的概率==.
故选:B.
11.(2020?山西模拟)在不透明的甲口袋中装有32个红球和8个黑球,在不透明的乙口袋中装有48个红球,20个黑球和32个白球.这些球除了颜色外没有其他区别.搅匀两口袋中的球,从口袋中分别任意摸出一个球,下列说法正确的是( )
A.从甲口袋中摸到黑球的概率较大
B.从乙口袋中摸到黑球的概率较大
C.从甲、乙两口袋中摸到黑球的概率相等
D.无法比较从甲、乙两口袋中摸到黑球的概率
【解析】解:∵甲口袋中装有32个红球和8个黑球,
球的总个数为:32+8=40个;
黑球的个数为:8个,
∵乙口袋中装有48个红球,20个黑球和32个白球,
球的总个数为:48+20+32=100个,
黑球的个数为:20个,
∴从甲口袋摸到黑球的概率==;
从乙口袋摸到黑球的概率==
∴从甲、乙两口袋中摸到黑球的概率相等,
故选:C.
12.(2021?新华区模拟)某市公园的东、南、西、北方向上各有一个入口,周末佳佳和琪琪随机从一个入口进入该公园游玩,则佳佳和琪琪恰好从同一个入口进入该公园的概率是( )
A.
B.
C.
D.
【解析】解:画树状图如下:
由树状图可知,共有16种等可能结果,其中佳佳和琪琪恰好从同一个入口进入该公园的有4种等可能结果,
所以佳佳和琪琪恰好从同一个入口进入该公园的概率为=,
故选:B.
二.填空题
13.(2020秋?五峰县期末)在一个箱子里放有2个白球和5个红球,现摸出1个球是黑球,这个事件属于 不可能 事件.(填“必然、不确定或不可能”)
【解析】解:在一个箱子里放有2个白球和5个红球,现摸出1个球是黑球,这个事件属于不可能事件,
故答案为:不可能.
14.(2020秋?天河区期末)在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数可能是 5 个.
【解析】解:设袋子中红球有x个,
根据题意,得:=0.25,
解得x=5,
即袋子中红球的个数可能是5个,
故答案为:5.
15.(2020秋?鄄城县期末)在一个不透明的袋子中装有6个白球和若干个红球,这些球除颜色外都相同.每次从袋子中随机摸出一个球,记下颜色后再放回袋中,通过多次重复试验发现摸出白球的频率稳定在0.3附近,则估计袋子中的红球有 14 个.
【解析】解:∵通过多次重复试验发现摸出白球的频率稳定在0.3附近,
∴从袋子中任意摸出1个球,是白球的概率约为0.3,
设袋子中红球有x个,
根据题意,得:=0.3,
解得x=14,
经检验:x=14是分式方程的解,
∴估计袋子中的红球有14个,
故答案为:14.
16.(2021?津南区模拟)在一个不透明的袋子中只装有n个白球和4个红球,这些球除颜色外其他均相同.如果从袋子中随机摸出一个球,摸到红球的概率是,那么n的值为 8 .
【解析】解:根据题意得,
解得n=8,
经检验:n=48是分式方程的解,
故答案为:8.
17.(2021?沙坪坝区校级模拟)不透明的袋子里装有除标号外完全一样的四个小球,小球上分别标有﹣5,﹣1,2,3这四个数字,从袋子中随机抽取一个小球,记标号为m,不放回后将袋子摇匀,再随机抽取一个小球,记标号为n,则m,n使得二次函数y=mx2+n的图象同时经过四个象限的概率为 .
【解析】解:画树状图如图:
共有12个等可能的结果,m,n使得二次函数y=mx2+n的图象同时经过四个象限的结果有8个,
∴m,n使得二次函数y=mx2+n的图象同时经过四个象限的概率为=,
故答案为:.
18.(2021?嘉兴)看了《田忌赛马》故事后,小杨用数学模型来分析:齐王与田忌的上中下三个等级的三匹马记分如表,每匹马只赛一场,两数相比,大数为胜,三场两胜则赢.已知齐王的三匹马出场顺序为10,8,6.若田忌的三匹马随机出场,则田忌能赢得比赛的概率为
.
马匹姓名
下等马
中等马
上等马
齐王
6
8
10
田忌
5
7
9
【解析】解:由于田忌的上、中等马分别比齐王的中、下等马强,当齐王的三匹马出场顺序为10,8,6时,田忌的马按5,9,7的顺序出场,田忌才能赢得比赛,
当田忌的三匹马随机出场时,双方马的对阵情况如下:
双方马的对阵中,只有一种对阵情况田忌能赢,
∴田忌能赢得比赛的概率为.
故答案为:.
19.(2021?长沙模拟)为了防止输入性“新冠肺炎”,某医院成立隔离治疗发热病人防控小组,决定从内科3位骨干医师中(含有甲)抽调2人组成.则甲一定会被抽调到防控小组的概率是 .
【解析】解:内科3位骨干医师分别即为甲、乙、丙,
画树状图如图:
共有6个等可能的结果,甲一定会被抽调到防控小组的结果有4个,
∴甲一定会被抽调到防控小组的概率==;
故答案为:.
三.解答题
20.(2021?萧山区二模)文具店购进了20盒“2B”铅笔,但在销售过程中,发现其中混入了若干“HB”铅笔.店员进行统计后,发现每盒铅笔中最多混入了2支“HB”铅笔,具体数据见下表:
混入“HB”铅笔数
0
1
2
盒数
6
m
n
(1)用等式写出m,n所满足的数量关系 m+n=14 ;
(2)从20盒铅笔中任意选取1盒:
①“盒中没有混入‘HB’铅笔”是 随机 事件(填“必然”、“不可能”或“随机”);
②若“盒中混入1支‘HB’铅笔”的概率为,求m和n的值.
【解析】解:(1)观察表格发现:6+m+n=20,
∴用等式写出m,n所满足的数量关系为m+n=14,
故答案为:m+n=14;
(2)①“盒中没有混入‘HB’铅笔”是随机事件,
故答案为:随机;
②∵“盒中混入1支‘HB’铅笔”的概率为,
∴=,
∴m=5,n=9.
21.(2018?贵阳模拟)如图,在3×3的方格纸中,点A,B,C,D,E分别位于格点上.
(1)从A,D,E三点中任意取一点,以所取的这一点及B,C为顶点画三角形,则所画三角形是直角三角形的概率是 ;
(2)从A,D,E三点中先后任意取两个不同的点,以所取的这两点及B,C为顶点画四边形,求所画四边形是平行四边形的概率(用树状图列表的方法求解)
【解析】解:(1)以所取的这一点及B,C为顶点画三角形有△ABC、△DBC、△EBC三种情况,
其中所画三角形是直角三角形的有△ABC、△DBC这2种结果,
所以所画三角形是直角三角形的概率是,
故答案为:;
(2)画树状图如下:
由树状图可知共有6种等可能结果,其中与以B、C为顶点所画四边形是平行四边形的有2种结果,
∴所画四边形是平行四边形的概率为=.
22.(2021?常州一模)如图,将等边三角形、圆、平行四边形这三种图形分别画在3张大小、质地均相同的正方形小纸板上,将这3张正方形小纸板放入一只不透明的袋子中.
(1)搅匀后从中摸出一张小纸板,摸出的纸板上的图形是中心对称图形的概率是 ;
(2)搅匀后从中摸出一张小纸板,记下纸板上图形的名称后放回袋子中,再从中摸出一张小纸板,求两次摸出的小纸板上的图形都是轴对称图形的概率.
【解析】解:(1)等边三角形是轴对称图形,圆既是轴对称图形也是中心对称图形,平行四边形是中心对称图形,
则摸出的纸板上的图形是中心对称图形的概率是,
故答案为:;
(2)把画有等边三角形、圆、平行四边形的正方形小纸板上分别记为A、B、C,画树状图如图:
共有9个等可能的结果,两次摸出的小纸板上的图形都是轴对称图形的结果有4个,
∴两次摸出的小纸板上的图形都是轴对称图形的概率为.
23.(2021春?无锡期中)一个不透明的口袋中放着若干个红球和黑球,这两种球除了颜色之外没有其他任何区别,袋中的球已经搅匀,闭眼从口袋中摸出一个球,经过很多次实验发现摸到红球的频率逐渐稳定在.
(1)估计摸到黑球的概率是 ;
(2)如果袋中原有红球12个,又放入n个黑球,再经过很多次实验发现摸到黑球的频率逐渐稳定在,求n的值.
【解析】解:(1)P(取出黑球)=1﹣P(取出红球)=1﹣=;
故答案为:;
(2)设袋子中原有黑球x个,
根据题意得:=,
解得:x=18,
经检验x=18是原方程的根,
所以黑球有18个,
∵又放入了n个黑球,
根据题意得:=,
解得:n=6.
24.(2021?滨城区一模)2021年上映的《你好,李焕英》票房破50亿,某中学就《你好,李焕英》电影的喜爱程度,在校内对部分学生进行了问卷调查,并对问卷调查的结果分为“非常喜欢”、“比较喜欢”、“感觉一般”、“不太喜欢”四个等级,分别记作A、B、C、D.根据调查结果绘制出如图所示的扇形统计图和条形统计图,请结合图中所给信息解答下列问题:
(1)本次被调查对象共有 50 人;扇形统计图中被调查者“比较喜欢”等级所对应圆心角的度数为 144° ;
(2)将条形统计图补充完整,并标明数据;
(3)若选“不太喜欢”的人中有两个女生和两个男生,从选“不太喜欢”的人中挑选两个学生了解不太喜欢的原因,请用列举法(画树状图或列表)求所选取的这两名学生恰好是一男一女的概率.
【解析】解:(1)本次被调查对象共有:16÷32%=50(人),
被调查者“比较喜欢”有:50﹣16﹣4﹣50×20%=20(人);
则扇形统计图中被调查者“比较喜欢”等级所对应圆心角的度数为360°×=144°
故答案为:50,144°;
(2)C等级的人数有:50﹣16﹣20﹣4=10(人),
将条形统计图补充完整如下:
(3)画树状图如图:
共有12个等可能的结果,所选取的这两名学生恰好是一男一女的结果有8个,
∴所选取的这两名学生恰好是一男一女的概率为=.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
