2.6 直角三角形同步练习（含解析）

中小学教育资源及组卷应用平台
浙教版八年级上
2.6直角三角形同步练习
一．选择题
1．（2021春?历下区期中）在下列条件：①∠A+∠B＝∠C，②∠A：∠B：∠C＝5：3：2，③∠A＝90°﹣∠B，④∠A＝2∠B＝3∠C中，能确定△ABC是直角三角形的条件有（　　）
A．1个
B．2个
C．3个
D．4个
2．（2020秋?嵊州市期中）直角三角形的两条直角边为3，4，则这个直角三角形斜边上的中线长为（　　）
A．5
B．2.5
C．3.5
D．4.5
3．（2019秋?新华区期中）如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足为D．下列结论中，不一定成立的是（　　）
A．∠A与∠1互余
B．∠B与∠2互余
C．∠A＝∠2
D．∠1＝∠2
4．（2020春?石狮市期末）在直角三角形ABC中，∠A：∠B：∠C＝2：m：4，则m的值是（　　）
A．3
B．4
C．2或6
D．2或4
5．（2021?任城区一模）如图，在△ABC中，AB＝AC，BE⊥AC，D是AB的中点，且DE＝BE，则∠C的度数是（　　）
A．65°
B．70°
C．75°
D．80°
6．（2020?温州模拟）如图，△ABC中，AB＝AC＝8，BC＝6，AE平分∠BAC交BC于点E，点D为AB的中点，连接DE，则△BDE的周长是（　　）
A．7+
B．10
C．4+2
D．11
7．（2020春?十堰期末）Rt△ABC中，∠C＝90°，锐角为30°，最短边长为5cm，则最长边上的中线是（　　）
A．5cm
B．15cm
C．10cm
D．2.5cm
二．填空题
8．（2020?余杭区一模）如图，在△ABC中，∠ACB＝90°，CD是△ABC的中线，若∠DCB＝40°，则∠A的度数为　
　°．
9．（2021春?金华月考）如图，在△ABC中，∠C＝90°，DE是AB的垂直平分线，且∠BAD：∠CAB＝1：3，则∠B＝　
　．
10．（2019秋?闽清县期中）如图，△ABC中，∠ACB＝90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处．若∠A＝22°，则∠ADE＝　
　°．
11．（2021?包河区三模）如图，已知△ABC中，∠ACB＝90°，O为AB的中点，点E在BC上，且CE＝AC，∠BAE＝15°，则∠COE＝　
　度．
12．（2020?武汉模拟）如图，在△ABC中，∠ACB＝90°，D为AB的中点，E为线段BD上一点，且AC＝CE，若∠DCE＝30°，则∠B的度数为　
　．
13．（2020春?西城区校级期中）如图，Rt△ABC中，∠ACB＝90°，CD⊥AB于点D．∠ACD＝3∠BCD，E是斜边中点，则∠ECD＝　
　°．
三．解答题
14．（2016秋?江干区期末）已知：如图，在△ABC中，AD是BC边上的高，∠B＝30°，∠ACB＝45°，CE是AB边上的中线．
（1）CD＝AB；
（2）若CG＝EG，求证：DG⊥CE．
15．（2020春?石阡县期末）如图，在△ABC中，CE，BF是两条高，若∠A＝70°，∠BCE＝30°，求∠EBF与∠FBC的度数．
16．（2020秋?江干区校级期中）如图，在四边形ABCD中，∠BAD＝∠BCD＝90°，点E，F分别是BD，AC的中点，连接EF．
（1）试判断EF与AC的位置关系，并说明理由；
（2）若∠EAF＝45°，求∠ADC的度数．
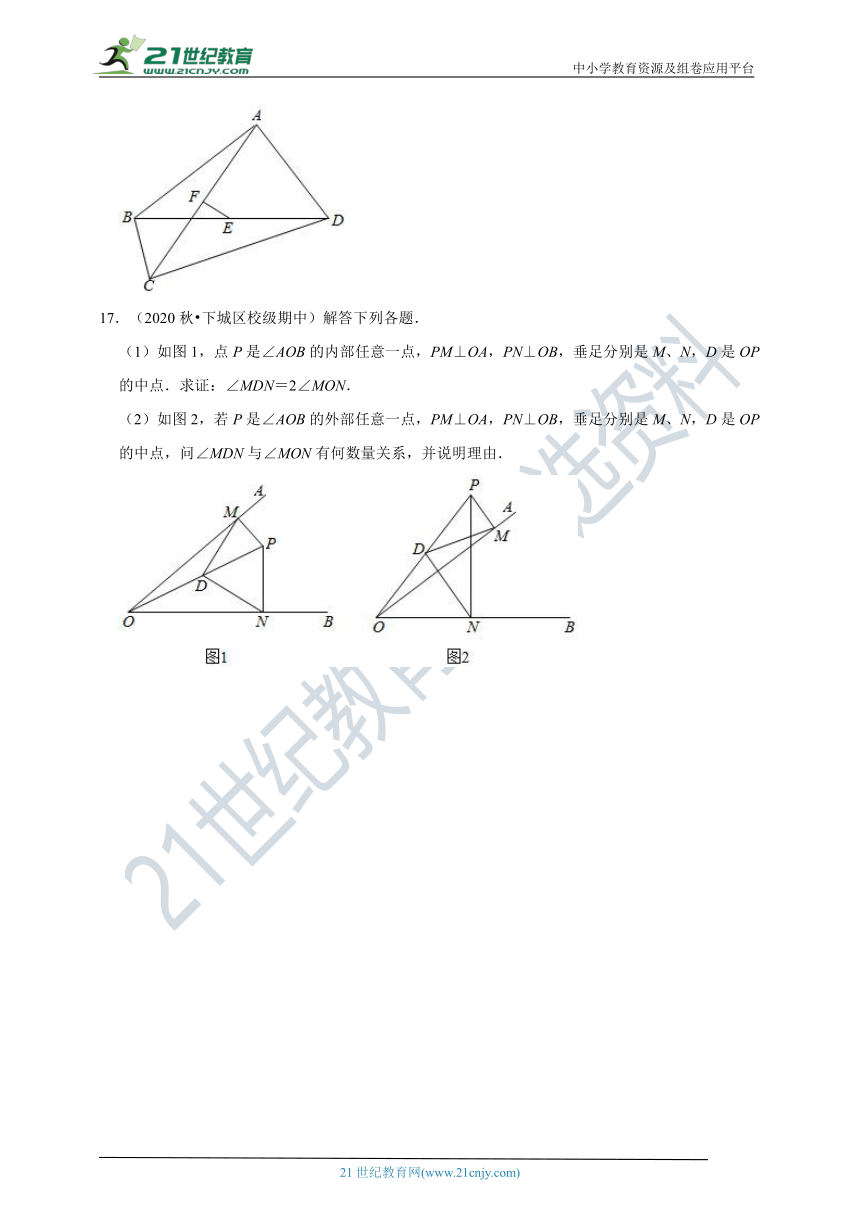
17．（2020秋?下城区校级期中）解答下列各题．
（1）如图1，点P是∠AOB的内部任意一点，PM⊥OA，PN⊥OB，垂足分别是M、N，D是OP的中点．求证：∠MDN＝2∠MON．
（2）如图2，若P是∠AOB的外部任意一点，PM⊥OA，PN⊥OB，垂足分别是M、N，D是OP的中点，问∠MDN与∠MON有何数量关系，并说明理由．
答案与解析
一．选择题
1．（2021春?历下区期中）在下列条件：①∠A+∠B＝∠C，②∠A：∠B：∠C＝5：3：2，③∠A＝90°﹣∠B，④∠A＝2∠B＝3∠C中，能确定△ABC是直角三角形的条件有（　　）
A．1个
B．2个
C．3个
D．4个
【解答】解：①∵∠A+∠B＝∠C，
∴2∠C＝180°，
∴∠C＝90°，
∴△ABC是直角三角形；
②∵∠A：∠B：∠C＝5：3：2，
设∠A＝5x，则∠B＝3x，∠C＝2x，
∴5x+2x+3x＝180，
解得：x＝18°，
∴∠5＝18°×5＝90°，
∴△ABC是直角三角形；
③∵∠A＝90°﹣∠B，
∴∠A+∠B＝90°，
∴∠C＝180°﹣90°＝90°，
∴△ABC是直角三角形；
④∵3∠C＝2∠B＝∠A，
∴∠A+∠B+∠C＝∠A+∠A+∠A＝180°，
∴∠A＝（）°，
∴△ABC为钝角三角形．
∴能确定△ABC是直角三角形的有①②③共3个，
故选：C．
2．（2020秋?嵊州市期中）直角三角形的两条直角边为3，4，则这个直角三角形斜边上的中线长为（　　）
A．5
B．2.5
C．3.5
D．4.5
【解答】解：由勾股定理得：直角三角形的斜边长是＝5，
所以＝2.5，
故选：B．
3．（2019秋?新华区期中）如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足为D．下列结论中，不一定成立的是（　　）
A．∠A与∠1互余
B．∠B与∠2互余
C．∠A＝∠2
D．∠1＝∠2
【解答】解：A、在Rt△ACD中，∠ADC＝90°，所以∠A与∠1互余，正确；
B、在Rt△BCD中，∠BDC＝90°，所以∠B与∠2互余，正确；
C、∵∠A+∠1＝90°，∠1+∠2＝90°，
∴∠A＝∠2，正确；
D、当∠A＝∠B时，AC＝BC，所以CD既是∠C的角平分线，也是斜边上的高与中线，所以∠1＝∠2，正确；当∠A≠∠B时，∠1≠∠2，错误；
故选：D．
4．（2020春?石狮市期末）在直角三角形ABC中，∠A：∠B：∠C＝2：m：4，则m的值是（　　）
A．3
B．4
C．2或6
D．2或4
【解答】解：设∠A、∠B、∠C的度数分别为2x、mx、4x，
当∠C为直角时，2x+mx＝4x，
解得，m＝2，
当∠B为直角时，2x+4x＝mx，
解得，m＝6，
故选：C．
5．（2021?任城区一模）如图，在△ABC中，AB＝AC，BE⊥AC，D是AB的中点，且DE＝BE，则∠C的度数是（　　）
A．65°
B．70°
C．75°
D．80°
【解答】解：∵BE⊥AC，
∴∠AEB＝90°，
∵D是AB的中点，
∴DE＝AB＝BD＝AD，
∵DE＝BE，
∴DE＝BE＝BD，
∴△BDE为等边三角形，
∴∠ABE＝60°，
∴∠A＝90°﹣60°＝30°，
∵AB＝AC，
∴∠C＝×（180°﹣30°）＝75°，
故选：C．
6．（2020?温州模拟）如图，△ABC中，AB＝AC＝8，BC＝6，AE平分∠BAC交BC于点E，点D为AB的中点，连接DE，则△BDE的周长是（　　）
A．7+
B．10
C．4+2
D．11
【解答】解：∵在△ABC中，AB＝AC＝6，AE平分∠BAC，
∴BE＝CE＝BC＝3，
又∵D是AB中点，
∴BD＝AB＝4，
∴DE是△ABC的中位线，
∴DE＝AC＝4，
∴△BDE的周长为BD+DE+BE＝3+4+4＝11．
故选：D．
7．（2020春?十堰期末）Rt△ABC中，∠C＝90°，锐角为30°，最短边长为5cm，则最长边上的中线是（　　）
A．5cm
B．15cm
C．10cm
D．2.5cm
【解答】解：∵∠C＝90°，∠B＝30°，
∴AB＝2AC＝10cm，
∵CD是AB的中线，
∴CD＝AB＝5cm．
故选：A．
二．填空题
8．（2020?余杭区一模）如图，在△ABC中，∠ACB＝90°，CD是△ABC的中线，若∠DCB＝40°，则∠A的度数为　50　°．
【解答】解：∵在△ABC中，∠ACB＝90°，CD是△ABC的中线，
∵BD＝CD＝AB，
∴∠B＝∠DCB＝40°，
∴∠A＝90°﹣∠B＝50°，
故答案为：50．
9．（2021春?金华月考）如图，在△ABC中，∠C＝90°，DE是AB的垂直平分线，且∠BAD：∠CAB＝1：3，则∠B＝　22.5°　．
【解答】解：∵DE是AB的垂直平分线，
∴AD＝BD，
∴∠B＝∠BAD，
设∠BAD＝x°，∠CAB＝3x°，
∴∠B＝x°，
∵∠C＝90°，
∴∠CAD+∠BAD+∠B＝90°，
∴3x+x＝90，
解得：x＝22.5，
∴∠B＝22.5°，
故答案为：22.5°．
10．（2019秋?闽清县期中）如图，△ABC中，∠ACB＝90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处．若∠A＝22°，则∠ADE＝　46　°．
【解答】解：△ABC中，∠ACB＝90°，∠A＝22°，
∴∠B＝90°﹣∠A＝68°，
由折叠的性质可得：∠CED＝∠B＝68°，∠BDC＝∠EDC，
∴∠ADE＝∠CED﹣∠A＝46°，
故答案为：46．
11．（2021?包河区三模）如图，已知△ABC中，∠ACB＝90°，O为AB的中点，点E在BC上，且CE＝AC，∠BAE＝15°，则∠COE＝　75　度．
【解答】解：∵∠ACB＝90°，CE＝AC，
∴∠CAE＝∠AEC＝45°，
∵∠BAE＝15°，
∴∠CAB＝60°，
∴∠B＝30°，
∵∠ACB＝90°，O为AB的中点，
∴CO＝BO＝AO＝AB，
∴△AOC是等边三角形，∠OCB＝∠B＝30°，
∴AC＝OC＝CE，
∴∠COE＝∠CEO＝（180°﹣30°）＝75°，
故答案为：75．
12．（2020?武汉模拟）如图，在△ABC中，∠ACB＝90°，D为AB的中点，E为线段BD上一点，且AC＝CE，若∠DCE＝30°，则∠B的度数为　40°　．
【解答】解：∵∠ACB＝90°，D为AB的中点，
∴CD＝AD＝BD，∠A+∠B＝90°，
∴∠DCB＝∠B，
∵∠DCE＝30°，
∴∠BCE＝∠DCB﹣∠DCE＝∠B﹣30°，
∵AC＝CE，
∴∠CEA＝∠A，
∵∠CEA＝∠BCE+∠B，
∴∠A＝∠B﹣30°+∠B＝2∠B﹣30°，
∴2∠B﹣30°+∠B＝90°，
∴∠B＝40°，
故答案为：40°．
13．（2020春?西城区校级期中）如图，Rt△ABC中，∠ACB＝90°，CD⊥AB于点D．∠ACD＝3∠BCD，E是斜边中点，则∠ECD＝　45　°．
【解答】解：∵∠ACB＝90°，∠ACD＝3∠BCD，
∴∠BCD＝90°×＝22.5°，
∠ACD＝90°×＝67.5°，
∵CD⊥AB，
∴∠B＝90°﹣22.5°＝67.5°，
∵E是AB的中点，∠ACB＝90°，
∴CE＝BE，
∴∠BCE＝∠B＝67.5°，
∴∠ECD＝∠BCE﹣∠BCD＝67.5°﹣22.5°＝45°，
故答案是：45．
三．解答题
14．（2016秋?江干区期末）已知：如图，在△ABC中，AD是BC边上的高，∠B＝30°，∠ACB＝45°，CE是AB边上的中线．
（1）CD＝AB；
（2）若CG＝EG，求证：DG⊥CE．
【解答】证明：（1）∵AD是BC边上的高，
∴AD⊥BC，
∵∠B＝30°，
∴AD＝AB，
∵∠ACB＝45°，
∴△ACD是等腰直角三角形，
∴CD＝AD，
∴CD＝AB；
（2）连接DE，如图所示：
∵CE是AB边上的中线，AD⊥BC，
∴DE是Rt△ABD斜边AB上的中线，
∴DE＝AB，
∵CD＝AB，
∴DE＝CD，
∵CG＝EG，
∴DG⊥CE．
15．（2020春?石阡县期末）如图，在△ABC中，CE，BF是两条高，若∠A＝70°，∠BCE＝30°，求∠EBF与∠FBC的度数．
【解答】解：在Rt△ABF中，∠A＝70°，CE，BF是两条高，
∴∠EBF＝20°，∠ECA＝20°，
又∵∠BCE＝30°，
∴∠ACB＝50°，
∴在Rt△BCF中∠FBC＝40°．
16．（2020秋?江干区校级期中）如图，在四边形ABCD中，∠BAD＝∠BCD＝90°，点E，F分别是BD，AC的中点，连接EF．
（1）试判断EF与AC的位置关系，并说明理由；
（2）若∠EAF＝45°，求∠ADC的度数．
【解答】解：（1）EF⊥AC．
理由：连接AE，CE．
∵∠BAD＝∠BCD＝90°，E是BD的中点，
∴AE＝BD，CE＝BD，
∴AE＝CE，
又∵F是AC的中点，
∴EF⊥AC．
（2）以E为圆心，BE长为半径画圆，
∵∠BAD+∠DCB＝90°+90°＝180°，
∴A、B、C、D四点共圆，且直径是BD，E为圆心，
∴∠BAC＝∠BDC，
∵∠EAF＝45°，
∴∠BAC+∠DAE＝45°，
∵AE＝DE，
∴∠ADB＝∠EAD，
∴∠ADC＝∠ADB+∠BDC＝∠BAC+∠EAD＝45°．
17．（2020秋?下城区校级期中）解答下列各题．
（1）如图1，点P是∠AOB的内部任意一点，PM⊥OA，PN⊥OB，垂足分别是M、N，D是OP的中点．求证：∠MDN＝2∠MON．
（2）如图2，若P是∠AOB的外部任意一点，PM⊥OA，PN⊥OB，垂足分别是M、N，D是OP的中点，问∠MDN与∠MON有何数量关系，并说明理由．
【解答】（1）证明：∵PM⊥OA，
∴∠OMP＝90°，
在Rt△OMP中，D是OP的中点，
∴DM＝OP＝DO，
∴∠DMO＝∠DOM，
∴∠MDP＝2∠MOP，
同理可知，∠NDP＝2∠NOP，
∴∠MDN＝∠MDP+∠NDP＝2∠MON；
（2）解：∠MDN＝2∠MON．
理由如下：如图2，∵PM⊥OA，
∴∠OMP＝90°，
在Rt△OMP中，D是OP的中点，
∴DM＝OP＝DO，
∴∠DMO＝∠DOM，
∴∠MDP＝2∠MOP，
同理可知，∠NDP＝2∠NOP，
∴∠MDN＝∠NDP﹣∠MDP＝2∠MON．
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
（共
2
页）
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)