2.7 探索勾股定理同步练习（含解析）

中小学教育资源及组卷应用平台
浙教版八年级上
2.7探索勾股定理同步练习
一．选择题
1．（2020秋?青田县期末）直角三角形的两条边长为5和12，它的斜边长为（　　）
A．13
B．
C．13或
D．13或12
2．（2020秋?柯桥区期中）如果三角形有一边上的中线长恰好等于这条边长，那么称这个三角形是“有趣三角形”，这条中线为“有趣中线”．如图，在△ABC中，∠C＝90°，较短的直角边BC＝，且△ABC是“有趣三角形”，则△ABC的“有趣中线”的长为（　　）
A．1
B．
C．2
D．
3．（2020秋?余杭区期中）如图，以Rt△ABC的三边为边长向外作正方形，三个正方形的面积分别为S1、S2、S3，若S1＝13，S2＝12，则S3的值为（　　）
A．1
B．5
C．25
D．144
4．（2020春?临海市期末）如图，每个小正方形的边长为1，四边形的顶点A，B，C，D都在格点上，则下面4条线段长度为的是（　　）
A．AB
B．BC
C．CD
D．AD
5．（2020?沭阳县模拟）如图，在△ABC中，AB＝AC＝5，BC＝6，点M为BC的中点，MN⊥AC于点N，则MN等于（　　）
A．1.5
B．2.4
C．2.5
D．3.5
6．（2020秋?诸暨市期中）如图，以Rt△ABC的三条边作三个正三角形，则S1、S2、S3、S4的关系为（　　）
A．S1+S2+S3＝S4
B．S1+S2＝S3+S4
C．S1+S3＝S2+S4
D．不能确定
7．（2020秋?萧山区期中）如图是“赵爽弦图”，△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形，四边形ABCD和EFGH都是正方形，如果AB＝10，EF＝2，那么AH等于（　　）
A．2
B．4
C．6
D．8
8．（2020春?南岸区期末）等腰三角形一腰长为5，这一腰上的高为3，则这个等腰三角形底边长为（　　）
A．
B．
C．或
D．4或
9．（2020秋?萧山区期中）已知直角三角形纸片的两条直角边长分别为m和3（m＜3），过锐角顶点把该纸片剪成两个三角形，若这两个三角形都为等腰三角形，则（　　）
A．m2+6m+9＝0
B．m2﹣6m+9＝0
C．m2+6m﹣9＝0
D．m2﹣6m﹣9＝0
10．（2020?金华）如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH．连接EG，BD相交于点O，BD与HC相交于点P．若GO＝GP，则的值是（　　）
A．1+
B．2+
C．5﹣
D．
二．填空题
11．（2020秋?乐清市期中）如图，已知Rt△ABC中，∠C＝90°，BC＝8，AC＝6，CD是斜边AB上的高，求AD的长度为　
　．
12．（2020秋?随县期末）如图，“人字梯”放在水平的地面上，AB＝AC，当梯子的一边与地面所夹的锐角α为60°时，两梯角之间的距离BC的长为2m．周日亮亮帮助妈妈整理换季衣服，先使α为60°，后又调整α为45°，则梯子顶端A离地面的高度下降了　
　m．
13．（2021春?拱墅区校级月考）如图在四边形ABCD中，∠ABC＝120°，AB⊥AD，BC⊥CD，AB＝4，CD＝5，则该四边形的面积是　
　．
14．（2019秋?余姚市期末）如图，在△ABC中，AC＝BC＝13，AB＝24，D是AB边上的一个动点，点E与点A关于直线CD对称，当△ADE为直角三角形时，则AD的长为　
　．
三．解答题
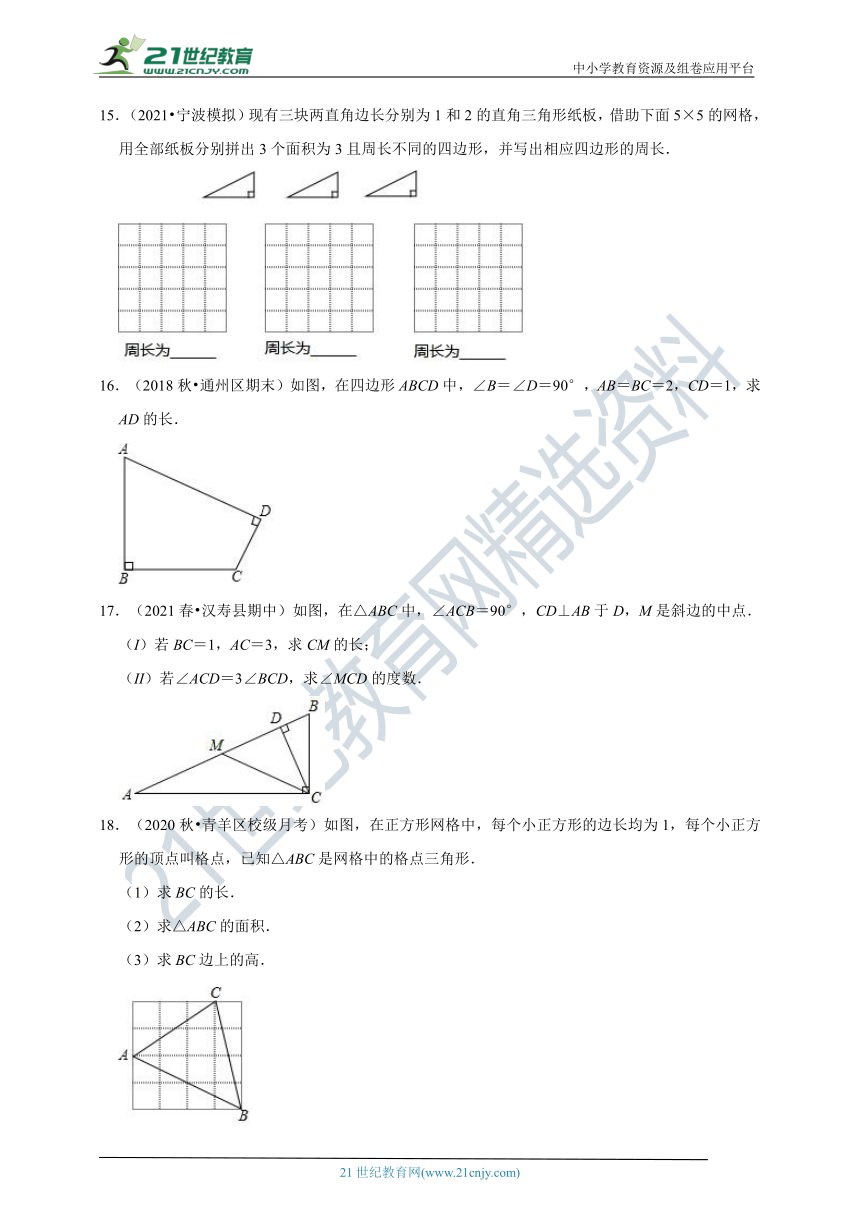
15．（2021?宁波模拟）现有三块两直角边长分别为1和2的直角三角形纸板，借助下面5×5的网格，用全部纸板分别拼出3个面积为3且周长不同的四边形，并写出相应四边形的周长．
16．（2018秋?通州区期末）如图，在四边形ABCD中，∠B＝∠D＝90°，AB＝BC＝2，CD＝1，求AD的长．
17．（2021春?汉寿县期中）如图，在△ABC中，∠ACB＝90°，CD⊥AB于D，M是斜边的中点．
（I）若BC＝1，AC＝3，求CM的长；
（II）若∠ACD＝3∠BCD，求∠MCD的度数．
18．（2020秋?青羊区校级月考）如图，在正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点叫格点，已知△ABC是网格中的格点三角形．
（1）求BC的长．
（2）求△ABC的面积．
（3）求BC边上的高．
19．（2020?上城区模拟）如图，△ABC中，∠ACB＝90°，AB＝5cm，BC＝3cm，若点P从点A出发，以每秒2cm的速度沿折线A﹣C﹣B﹣A运动，设运动时间为t秒（t＞0）．
（1）若点P在AC上，且满足PA＝PB时，求出此时t的值；
（2）若点P恰好在∠BAC的角平分线上，求t的值；
（3）在运动过程中，直接写出当t为何值时，△BCP为等腰三角形．
答案与解析
一．选择题
1．（2020秋?青田县期末）直角三角形的两条边长为5和12，它的斜边长为（　　）
A．13
B．
C．13或
D．13或12
【解析】解：当12是直角边时，斜边长＝＝13；
当12是斜边时，斜边长＝12．
故它的斜边长为13或12．
故选：D．
2．（2020秋?柯桥区期中）如果三角形有一边上的中线长恰好等于这条边长，那么称这个三角形是“有趣三角形”，这条中线为“有趣中线”．如图，在△ABC中，∠C＝90°，较短的直角边BC＝，且△ABC是“有趣三角形”，则△ABC的“有趣中线”的长为（　　）
A．1
B．
C．2
D．
【解析】解：“有趣中线”有三种情况：
①若“有趣中线”为斜边AB上的中线，直角三角形的斜边的中线等于斜边的一半，不合题意；
②若“有趣中线”为BC边上的中线，如图1，AD＝BC＝，
∴CD＝，
根据勾股定理得：AC＝＝＜，不符合题意；
③若“有趣中线”为另一直角边AC上的中线，如图2所示，BC＝，
设BD＝2x，则CD＝x，
在Rt△CBD中，根据勾股定理得：BD2＝BC2+CD2，即（2x）2＝（）2+x2，
解得：x＝1，
∴BD＝2，
则△ABC的“有趣中线”的长等于2．
故选：C．
3．（2020秋?余杭区期中）如图，以Rt△ABC的三边为边长向外作正方形，三个正方形的面积分别为S1、S2、S3，若S1＝13，S2＝12，则S3的值为（　　）
A．1
B．5
C．25
D．144
【解析】解：由勾股定理得：AC2+BC2＝AB2，
∵S1＝S2+S3，
∴S3＝S1﹣S2＝13﹣12＝1．
故选：A．
4．（2020春?临海市期末）如图，每个小正方形的边长为1，四边形的顶点A，B，C，D都在格点上，则下面4条线段长度为的是（　　）
A．AB
B．BC
C．CD
D．AD
【解析】解：AB＝＝，BC＝3，CD＝＝，AD＝＝，
故长度为的线段是AB，
故选：A．
5．（2020?沭阳县模拟）如图，在△ABC中，AB＝AC＝5，BC＝6，点M为BC的中点，MN⊥AC于点N，则MN等于（　　）
A．1.5
B．2.4
C．2.5
D．3.5
【解析】解：连接AM，
∵AB＝AC，点M为BC中点，
∴AM⊥CM（三线合一），BM＝CM，
∵AB＝AC＝5，BC＝6，
∴BM＝CM＝3，
在Rt△ABM中，AB＝5，BM＝3，
∴根据勾股定理得：AM＝＝＝4，
又S△AMC＝MN?AC＝AM?MC，
∴MN＝＝＝2.4．
故选：B．
6．（2020秋?诸暨市期中）如图，以Rt△ABC的三条边作三个正三角形，则S1、S2、S3、S4的关系为（　　）
A．S1+S2+S3＝S4
B．S1+S2＝S3+S4
C．S1+S3＝S2+S4
D．不能确定
【解析】解：如图，设Rt△ABC的三条边AB＝c，AC＝b，BC＝a，
∵△ACG，△BCH，△ABF是等边三角形，
∴S1＝S△ACG﹣S5＝b2﹣S5，S3＝S△BCH﹣S6＝a2﹣S6，
∴S1+S3＝（a2+b2）﹣S5﹣S6，
∵S2+S4＝S△ABF﹣S5﹣S6＝c2﹣S5﹣S6，
∵c2＝a2+b2，
∴S1+S3＝S2+S4，
故选：C．
7．（2020秋?萧山区期中）如图是“赵爽弦图”，△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形，四边形ABCD和EFGH都是正方形，如果AB＝10，EF＝2，那么AH等于（　　）
A．2
B．4
C．6
D．8
【解析】解：∵AB＝10，EF＝2，
∴大正方形的面积是100，小正方形的面积是4，
∴四个直角三角形面积和为100﹣4＝96，设AE为a，DE为b，即4×ab＝96，
∴2ab＝96，a2+b2＝100，
∴（a+b）2＝a2+b2+2ab＝100+96＝196，
∴a+b＝14，
∵a﹣b＝2，
解得：a＝8，b＝6，
∴AE＝8，DE＝6，
∴AH＝8﹣2＝6．
故选：C．
8．（2020春?南岸区期末）等腰三角形一腰长为5，这一腰上的高为3，则这个等腰三角形底边长为（　　）
A．
B．
C．或
D．4或
【解析】解：分两种情况：
（1）顶角是钝角时，如图1所示：
（2）
在Rt△ACO中，由勾股定理，得AO2＝AC2﹣OC2＝52﹣32＝16，
∴AO＝4，
OB＝AB+AO＝5+4＝9，
在Rt△BCO中，由勾股定理，得BC2＝OB2+OC2＝92+32＝90，
∴BC＝＝3；
（2）顶角是锐角时，如图2所示：
在Rt△ACD中，由勾股定理，得AD2＝AC2﹣DC2＝52﹣32＝16，
∴AD＝4，
DB＝AB﹣AD＝5﹣4＝1．
在Rt△BCD中，由勾股定理，得BC2＝DB2+DC2＝12+32＝10，
∴BC＝；
综上可知，这个等腰三角形的底的长度为3或．
故选：C．
9．（2020秋?萧山区期中）已知直角三角形纸片的两条直角边长分别为m和3（m＜3），过锐角顶点把该纸片剪成两个三角形，若这两个三角形都为等腰三角形，则（　　）
A．m2+6m+9＝0
B．m2﹣6m+9＝0
C．m2+6m﹣9＝0
D．m2﹣6m﹣9＝0
【解析】解：如图，
m2+m2＝（3﹣m）2，
2m2＝32﹣6m+m2，
m2+6m﹣9＝0．
故选：C．
10．（2020?金华）如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH．连接EG，BD相交于点O，BD与HC相交于点P．若GO＝GP，则的值是（　　）
A．1+
B．2+
C．5﹣
D．
【解析】解：∵四边形EFGH为正方形，
∴∠EGH＝45°，∠FGH＝90°，
∵OG＝GP，
∴∠GOP＝∠OPG＝67.5°，
∴∠PBG＝22.5°，
又∵∠DBC＝45°，
∴∠GBC＝22.5°，
∴∠PBG＝∠GBC，
∵∠BGP＝∠BGC＝90°，BG＝BG，
∴△BPG≌△BCG（ASA），
∴PG＝CG．
设OG＝PG＝CG＝x，
∵O为EG，BD的交点，
∴EG＝2x，FG＝x，
∵四个全等的直角三角形拼成“赵爽弦图”，
∴BF＝CG＝x，
∴BG＝x+x，
∴BC2＝BG2+CG2＝＝，
∴＝．
故选：B．
二．填空题
11．（2020秋?乐清市期中）如图，已知Rt△ABC中，∠C＝90°，BC＝8，AC＝6，CD是斜边AB上的高，求AD的长度为　　．
【解析】解：Rt△ABC中，∠C＝90°，
∴AB＝＝＝10，
∴S△ABC＝×AC×BC＝×AB×CD，即×6×8＝×10×CD，
解得，CD＝
在Rt△ACD中，AD＝＝＝，
故答案为：．
12．（2020秋?随县期末）如图，“人字梯”放在水平的地面上，AB＝AC，当梯子的一边与地面所夹的锐角α为60°时，两梯角之间的距离BC的长为2m．周日亮亮帮助妈妈整理换季衣服，先使α为60°，后又调整α为45°，则梯子顶端A离地面的高度下降了　（﹣）　m．
【解析】解：如图1所示：
过点A作AD⊥BC于点D，
由题意可得：∠B＝∠C＝60°，
则△ABC是等边三角形，
故BC＝AB＝AC＝2m，
则AD＝2sin60°＝m，
如图2所示：
过点A作AE⊥BC于点E，
由题意可得：∠B＝∠C＝60°，
则△ABC是等腰直角三角形，AC＝AB，
则AE＝BC＝m，
故梯子顶端离地面的高度AD下降了（﹣）m．
故答案为：（﹣）．
13．（2021春?拱墅区校级月考）如图在四边形ABCD中，∠ABC＝120°，AB⊥AD，BC⊥CD，AB＝4，CD＝5，则该四边形的面积是　　．
【解析】解：延长DA和CB交于O，
∵AB⊥AD，BC⊥CD，
∴∠DAB＝∠C＝∠OAB＝90°，
∵∠D＝60°，
∴∠O＝30°，
∵AB＝4，DC＝5，
∴OB＝2AB＝8，OD＝2DC＝10，
由勾股定理得：OA＝＝4，OC＝＝5，
∴四边形ABCD的面积是S△OCD﹣S△OAB＝×OC×CD﹣×OA×AB＝×5×5﹣×4×4＝．
故答案为．
14．（2019秋?余姚市期末）如图，在△ABC中，AC＝BC＝13，AB＝24，D是AB边上的一个动点，点E与点A关于直线CD对称，当△ADE为直角三角形时，则AD的长为　7或17　．
【解析】解：作CF⊥AB于F，
∵在△ABC中，AC＝BC＝13，AB＝24，
∴AF＝12，
∴CF＝＝5，
①如图1，当点D在AF上时，
∵∠ADE＝90°，
∴∠ADC＝∠EDC＝（360°﹣90°）÷2＝135°．
∴∠CDF＝45°．
∴CF＝DF．
∴AD＝AF﹣DF＝AF﹣CF＝12﹣5＝7．
②如图2，当点D在BF上时，
∵∠ADE＝90°，
∴∠CDF＝45°．
∴CF＝DF．
∴AD＝AF+DF＝AF+CF＝12+5＝17．
三．解答题
15．（2021?宁波模拟）现有三块两直角边长分别为1和2的直角三角形纸板，借助下面5×5的网格，用全部纸板分别拼出3个面积为3且周长不同的四边形，并写出相应四边形的周长．
【解析】解；如图所示：
16．（2018秋?通州区期末）如图，在四边形ABCD中，∠B＝∠D＝90°，AB＝BC＝2，CD＝1，求AD的长．
【解析】解：连接AC，
∵∠B＝90°
∴AC2＝AB2+BC2．
∵AB＝BC＝2
∴AC2＝8．
∵∠D＝90°
∴AD2＝AC2﹣CD2．
∵CD＝1，
∴AD2＝7．
∴．
17．（2021春?汉寿县期中）如图，在△ABC中，∠ACB＝90°，CD⊥AB于D，M是斜边的中点．
（I）若BC＝1，AC＝3，求CM的长；
（II）若∠ACD＝3∠BCD，求∠MCD的度数．
【解析】解：（Ⅰ）∵在△ABC中，∠ACB＝90°，BC＝1，AC＝3，
∴AB＝＝，
∵M是斜边的中点，
∴CM＝AB＝；
（Ⅱ）∵∠ACB＝∠ACD+∠BCD＝90°，∠ACD＝3∠BCD，
∴∠ACD＝90°×＝67.5°，
∵CD⊥AB，
∴∠A+∠ACD＝90°，
∴∠A＝22.5°，
∵CM＝AB＝AM，
∴∠ACM＝∠A＝22.5°，
∴∠MCD＝∠ACD﹣∠ACM＝67.5°﹣22.5°＝45°．
18．（2020秋?青羊区校级月考）如图，在正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点叫格点，已知△ABC是网格中的格点三角形．
（1）求BC的长．
（2）求△ABC的面积．
（3）求BC边上的高．
【解析】解：（1）由图可知：BC＝＝．
（2）如图，
S△ABC＝S正方形EDBF﹣S△BCF﹣S△ABD﹣S△ACE
＝4×4﹣×1×4﹣×2×4﹣×2×3
＝16﹣2﹣4﹣3
＝7．
（3）过点A作AH⊥BC于点H，
∵S△ABC＝×BC×AH，
∴7＝×AH，
∴AH＝．
∴BC边上的高为．
19．（2020?上城区模拟）如图，△ABC中，∠ACB＝90°，AB＝5cm，BC＝3cm，若点P从点A出发，以每秒2cm的速度沿折线A﹣C﹣B﹣A运动，设运动时间为t秒（t＞0）．
（1）若点P在AC上，且满足PA＝PB时，求出此时t的值；
（2）若点P恰好在∠BAC的角平分线上，求t的值；
（3）在运动过程中，直接写出当t为何值时，△BCP为等腰三角形．
【解析】解：（1）设存在点P，使得PA＝PB，
此时PA＝PB＝2t，PC＝4﹣2t，
在Rt△PCB中，PC2+CB2＝PB2，
即：（4﹣2t）2+32＝（2t）2，
解得：t＝，
∴当t＝时，PA＝PB；
（2）当点P在∠BAC的平分线上时，如图1，过点P作PE⊥AB于点E，
此时BP＝7﹣2t，PE＝PC＝2t﹣4，BE＝5﹣4＝1，
在Rt△BEP中，PE2+BE2＝BP2，
即：（2t﹣4）2+12＝（7﹣2t）2，
解得：t＝，
当t＝6时，点P与A重合，也符合条件，
∴当或6时，P在△ABC的角平分线上；
（3）在Rt△ABC中，∵AB＝5cm，BC＝3cm，
∴AC＝4cm，
根据题意得：AP＝2t，
当P在AC上时，△BCP为等腰三角形，
∴PC＝BC，即4﹣2t＝3，
∴t＝，
当P在AB上时，△BCP为等腰三角形，
①CP＝PB，点P在BC的垂直平分线上，
如图2，过P作PE⊥BC于E，
∴BE＝BC＝，
∴PB＝AB，即2t﹣3﹣4＝，解得：t＝，
②PB＝BC，即2t﹣3﹣4＝3，
解得：t＝5，
③PC＝BC，如图3，过C作CF⊥AB于F，
∴BF＝BP，
∵∠ACB＝90°，
由射影定理得；BC2＝BF?AB，
即32＝×5，
解得：t＝，
∴当时，△BCP为等腰三角形．
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
（共
2
页）
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)