1.5三角形全等的判定 同步能力提升专题训练 2021-2022学年浙教版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 1.5三角形全等的判定 同步能力提升专题训练 2021-2022学年浙教版八年级数学上册(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 433.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 00:00:00 | ||
图片预览



文档简介
2021-2022学年浙教版八年级数学上册《1.5三角形全等的判定》
同步能力提升专题训练(附答案)
一.全等三角形的判定
1.如图,AB=DB,∠ABD=∠CBE,①BE=BC,②∠D=∠A,③∠C=∠E,④AC=DE,能使△ABC≌△DBE的条件有( )个.
A.1
B.2
C.3
D.4
2.如图,AB,CD相交于点E,且AB=CD,试添加一个条件使得△ADE≌△CBE.现给出如下五个条件:①∠A=∠C;②∠B=∠D;③AE=CE;④BE=DE;⑤AD=CB.其中符合要求有( )
A.2个
B.3个
C.4个
D.5个
3.如图,已知四边形ABCD中,AB=10厘米,BC=8厘米,CD=12厘米,∠B=∠C,点E为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为
时,能够使△BPE与△CQP全等.
4.如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC与△DEC全等.
5.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.求证:△AEC≌△BED.
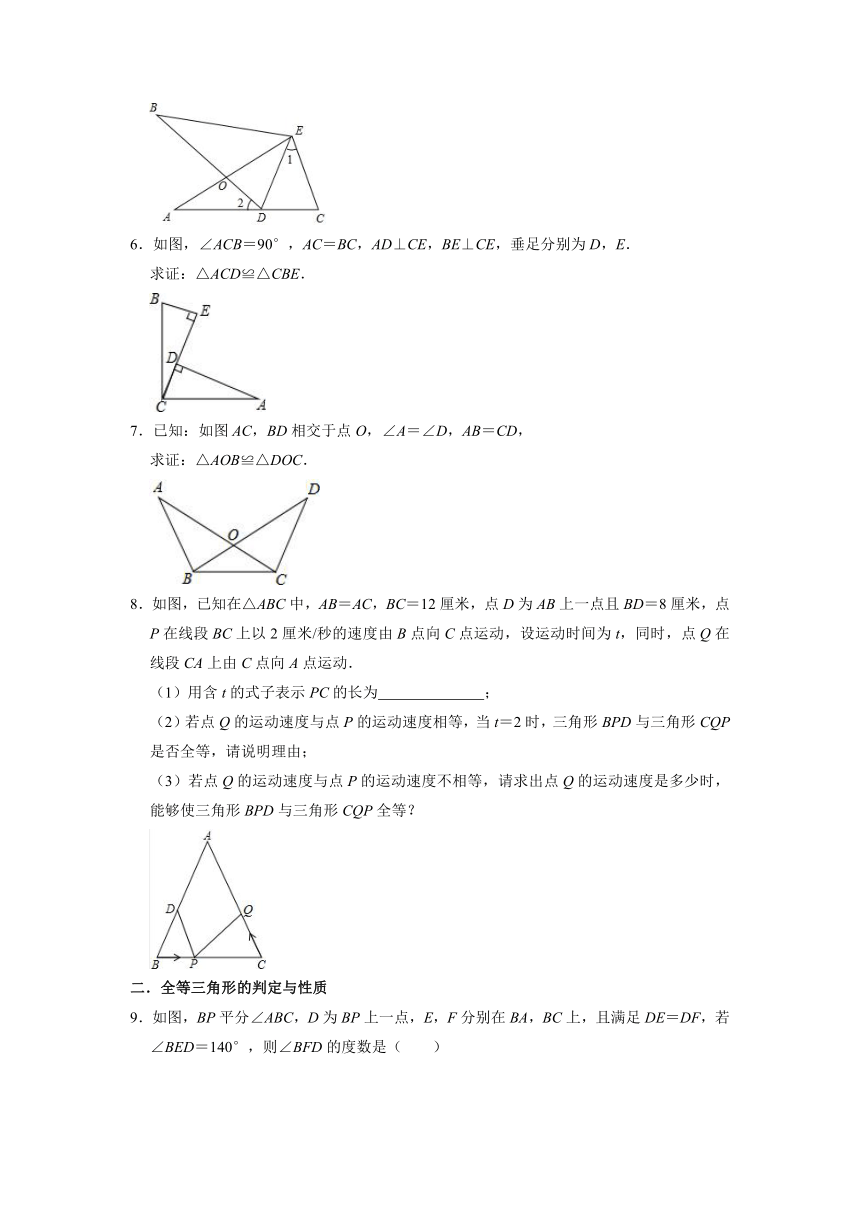
6.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.
求证:△ACD≌△CBE.
7.已知:如图AC,BD相交于点O,∠A=∠D,AB=CD,
求证:△AOB≌△DOC.
8.如图,已知在△ABC中,AB=AC,BC=12厘米,点D为AB上一点且BD=8厘米,点P在线段BC上以2厘米/秒的速度由B点向C点运动,设运动时间为t,同时,点Q在线段CA上由C点向A点运动.
(1)用含t的式子表示PC的长为
;
(2)若点Q的运动速度与点P的运动速度相等,当t=2时,三角形BPD与三角形CQP是否全等,请说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,请求出点Q的运动速度是多少时,能够使三角形BPD与三角形CQP全等?
二.全等三角形的判定与性质
9.如图,BP平分∠ABC,D为BP上一点,E,F分别在BA,BC上,且满足DE=DF,若∠BED=140°,则∠BFD的度数是( )
A.40°
B.50°
C.60°
D.70°
10.如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2cm,BE=0.5cm,则DE=
cm.
11.如图,△ABC中,AB=AC,点E,F在边BC上;BE=CF.
(1)求证:△ABE≌△ACF;
(2)若D在AF的延长线上,AD=AC,∠BAE=30°,∠BAD=75°,求证:AB∥DC.
12.如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD所在直线的位置关系为
,线段CF、BD的数量关系为
;
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.
13.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
14.如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,CE⊥BD于点E.
求证:AD=BE.
15.如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD.
16.如图,在△ABC中,AB=AC=8,BC=12,点D从B出发以每秒2个单位的速度在线段BC上从点B向点C运动,点E同时从C出发以每秒2个单位的速度在线段CA上向点A运动,连接AD、DE,设D、E两点运动时间为t秒(0<t<4)
(1)运动
秒时,AE=DC;
(2)运动多少秒时,△ABD≌△DCE能成立,并说明理由;
(3)若△ABD≌△DCE,∠BAC=α,则∠ADE=
(用含α的式子表示).
17.如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,AD交BE于O.求证:AD与BE互相平分.
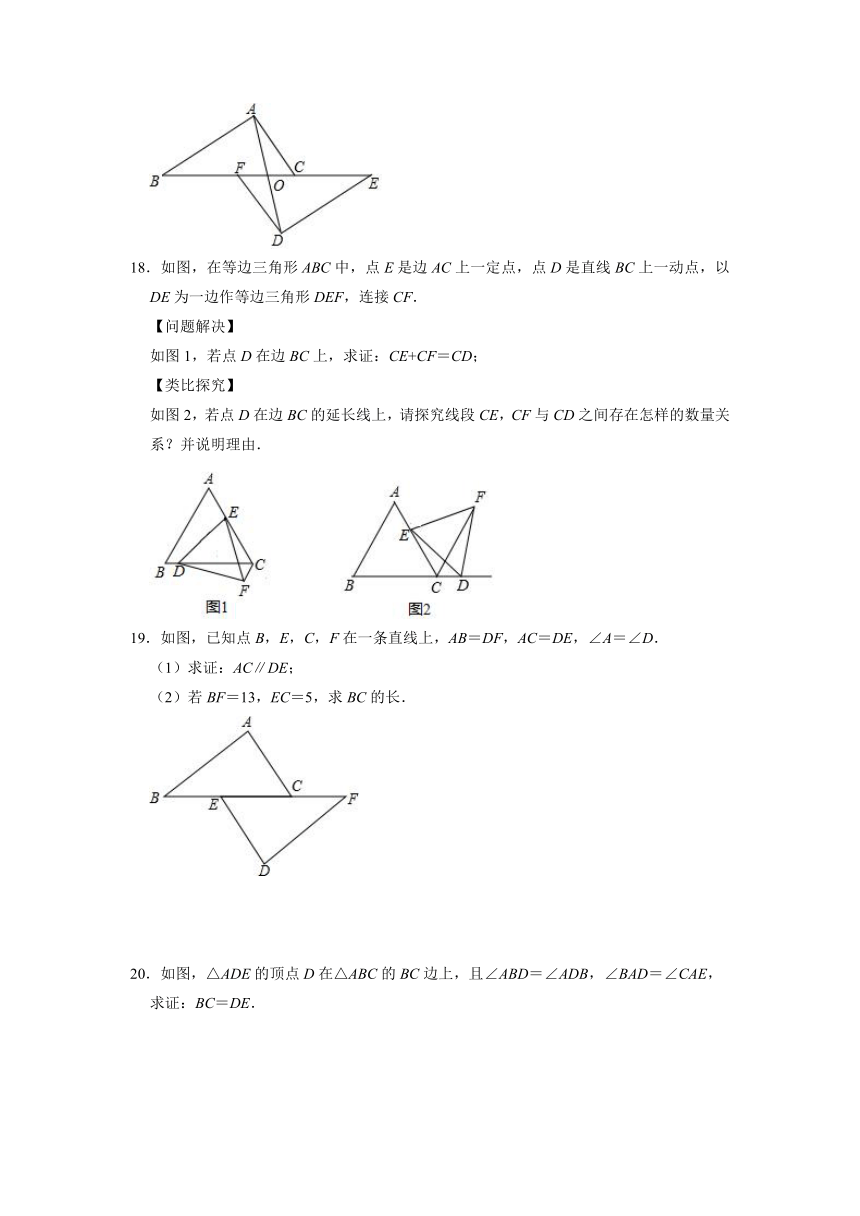
18.如图,在等边三角形ABC中,点E是边AC上一定点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.
【问题解决】
如图1,若点D在边BC上,求证:CE+CF=CD;
【类比探究】
如图2,若点D在边BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系?并说明理由.
19.如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.
(1)求证:AC∥DE;
(2)若BF=13,EC=5,求BC的长.
20.如图,△ADE的顶点D在△ABC的BC边上,且∠ABD=∠ADB,∠BAD=∠CAE,
求证:BC=DE.
21.如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.
22.如图,在△ABC中,∠ACB=45°,过点A作AD⊥BC于点D,点E为AD上一点,且ED=BD.
(1)求证:△ABD≌△CED;
(2)若CE为∠ACD的角平分线,求∠BAC的度数.
23.如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD.求证:AE=FB.
24.如图,AB∥CD,E、F分别为AB、CD上的点,且EC∥BF,连接AD,分别与EC、BF相交于点G,H,若AB=CD,求证:AG=DH.
25.已知:如图,点A、D、C、B在同一条直线上,AD=BC,AE=BF,CE=DF,求证:AE∥FB.
26.如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰三角形CDE,其中∠DCE=90°,连接BE.
(1)求证:△ACD≌△BCE;
(2)若AB=3cm,则BE=
cm.
(3)BE与AD有何位置关系?请说明理由.
27.如图,已知AB=AD,AC=AE,∠1=∠2,求证:BC=DE.
28.如图所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,垂足分别为E、F,且AB=CD.
(1)△ABF与△CDE全等吗?为什么?
(2)求证:EG=FG.
三.全等三角形的应用
29.如图,A,B两建筑物位于河的两岸,要测它们之间的距离,可以从B点出发在河岸上画一条射线BF,在BF上截取BC=CD,过点D作DE∥AB,使E,C,A在同一直线上,则DE的长就是A,B之间的距离,请你说明道理.
30.某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
①在河流的一条岸边B点,选对岸正对的一棵树A;
②沿河岸直走20m有一树C,继续前行20m到达D处;
③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;
④测得DE的长为5米.
求:(1)河的宽度是多少米?
(2)请你证明他们做法的正确性.
参考答案
一.全等三角形的判定
1.解:∵AB=DB,∠ABD=∠CBE,
∴∠ABC=∠DBE,
∵BE=BC,利用SAS可得△ABC≌△DBE;
∵∠D=∠A,利用ASA可得△ABC≌△DBE;
∵∠C=∠E,利用AAS可得△ABC≌△DBE;
故选:C.
2.解:延长DA、BC使它们相交于点F.
∵∠DAB=∠BCD,∠AED=∠BEC,
∴∠B=∠D,
又∵∠F=∠F,AB=CD,
∴△FAB≌△FCD
∴AF=FC,FD=FB,
∴AD=BC
∴△ADE≌△CBE①对
同理可得②对
∵AE=CE,AB=CD
∴DE=BE
又∵∠AED=∠BEC
∴△ADE≌△CBE(SAS)③对
同理可得④对
连接BD,∵AD=CB,AB=CD,BD=BD,
∴△ADB≌△CBD,
∴∠A=∠C,
∴△ADE≌△CBE,故⑤正确,
故选:D.
3.解:设点P运动的时间为t秒,则BP=3t,CP=8﹣3t,
∵∠B=∠C,
∴①当BE=CP=5,BP=CQ时,△BPE与△CQP全等,
此时,5=8﹣3t,
解得t=1,
∴BP=CQ=3,
此时,点Q的运动速度为3÷1=3厘米/秒;
②当BE=CQ=5,BP=CP时,△BPE与△CQP全等,
此时,3t=8﹣3t,
解得t=,
∴点Q的运动速度为5÷=厘米/秒;
故答案为:3厘米/秒或厘米/秒.
4.解:∵∠BCE=∠ACD=90°,
∴∠3+∠4=∠4+∠5,
∴∠3=∠5,
在△ACD中,∠ACD=90°,
∴∠2+∠D=90°,
∵∠BAE=∠1+∠2=90°,
∴∠1=∠D,
在△ABC和△DEC中,
,
∴△ABC≌△DEC(AAS).
5.证明:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,
∠A=∠B,∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA).
6.证明:∵AD⊥CE,BE⊥CE,
∴∠ADC=∠E=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∵∠B+∠BCE=90°,
∴∠B=∠ACD,
在△BEC和△CDA中,,
∴△ACD≌△CBE(AAS).
7.证明:在△AOB和△DOC中,,
所以,△AOB≌△DOC(AAS).
8.解:(1)BP=2t,则PC=BC﹣BP=12﹣2t;
故答案为(12﹣2t)cm
(2)当t=2时,BP=CQ=2×2=4厘米,
∵BD=8厘米.
又∵PC=BC﹣BP,BC=12厘米,
∴PC=12﹣4=8厘米,
∴PC=BD,
又∵AB=AC,
∴∠B=∠C,
在△BPD和△CQP中,,
∴△BPD≌△CQP(SAS);
③∵vP≠vQ,
∴BP≠CQ,
又∵△BPD≌△CPQ,∠B=∠C,
∴BP=PC=6cm,CQ=BD=8cm,
∴点P,点Q运动的时间t===3秒,
∴VQ==厘米/秒.
即点Q的运动速度是厘米/秒时,能够使三角形BPD与三角形CQP全等.
二.全等三角形的判定与性质
9.解:作DG⊥AB于G,DH⊥BC于H,
∵D是∠ABC平分线上一点,DG⊥AB,DH⊥BC,
∴DH=DG,
在Rt△DEG和Rt△DFH中,
,
∴Rt△DEG≌Rt△DFH(HL),
∴∠DEG=∠DFH,又∠DEG+∠BED=180°,
∴∠BFD+∠BED=180°,
∴∠BFD的度数=180°﹣140°=40°,
故选:A.
10.解:∵BE⊥CE,AD⊥CE
∴∠E=∠ADC=90°
∴∠DAC+∠DCA=90°
∵∠ACB=90°
∴∠BCE+∠DCA=90°
∴∠DAC=∠BCE
在△ACD和△CBE中,
,
∴△ACD≌△CBE
∴BE=CD=0.5(cm),EC=AD=2(cm)
DE=CE﹣CD=1.5(cm),
故答案为1.5
11.证明:∵AB=AC,
∴∠B=∠ACF,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(SAS);
(2)∵△ABE≌△ACF,∠BAE=30°,
∴∠BAE=∠CAF=30°,
∵AD=AC,
∴∠ADC=∠ACD,
∴∠ADC==75°,
∵∠BAD=75°,
∴∠BAD=∠ADC,
∴AB∥DC.
12.证明:(1)①正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
又∵AB=AC,
∴△DAB≌△FAC,
∴CF=BD,∠B=∠ACF,
∴∠ACB+∠ACF=90°,即CF⊥BD.
②当点D在BC的延长线上时①的结论仍成立.
由正方形ADEF得AD=AF,∠DAF=90度.
∵∠BAC=90°,
∴∠DAF=∠BAC,
∴∠DAB=∠FAC,
又∵AB=AC,
∴△DAB≌△FAC,
∴CF=BD,∠ACF=∠ABD.
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∴∠ACF=45°,
∴∠BCF=∠ACB+∠ACF=90度.
即CF⊥BD.
(2)当∠ACB=45°时,CF⊥BD(如图).
理由:过点A作AG⊥AC交CB的延长线于点G,
则∠GAC=90°,
∵∠ACB=45°,∠AGC=90°﹣∠ACB,
∴∠AGC=90°﹣45°=45°,
∴∠ACB=∠AGC=45°,
∴AC=AG,
∵∠DAG=∠FAC(同角的余角相等),AD=AF,
∴△GAD≌△CAF,
∴∠ACF=∠AGC=45°,
∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.
13.解:(1)证明:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,
∠A=∠B,∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA).
(2)∵△AEC≌△BED,
∴EC=ED,∠C=∠BDE.
在△EDC中,
∵EC=ED,∠1=42°,
∴∠C=∠EDC=69°,
∴∠BDE=∠C=69°.
14.证明:∵AD∥BC,
∴∠ADB=∠DBC.
∵CE⊥BD,
∴∠BEC=90°.
∵∠A=90°,
∴∠A=∠BEC.
∵BD=BC,
∴△ABD≌△BCE.
∴AD=BE.
15.证明:∵BD⊥AC于点D,CE⊥AB于点E,
∴∠ADB=∠AEC=90°,
在△ADB和△AEC中,
∴△ADB≌△AEC(ASA)
∴AB=AC,
又∵AD=AE,
∴BE=CD.
16.解:(1)由题可得,BD=CE=2t,
∴CD=12﹣2t,AE=8﹣2t,
∴当AE=DC,时,8﹣2t=(12﹣2t),
解得t=3,
故答案为:3;
(2)当△ABD≌△DCE成立时,AB=CD=8,
∴12﹣2t=8,
解得t=2,
∴运动2秒时,△ABD≌△DCE能成立;
(3)当△ABD≌△DCE时,∠CDE=∠BAD,
又∵∠ADE=180°﹣∠CDE﹣∠ADB,∠B=∠180°﹣∠BAD﹣∠ADB,
∴∠ADE=∠B,
又∵∠BAC=α,AB=AC,
∴∠ADE=∠B=(180°﹣α)=90°﹣α.
故答案为:90°﹣α.
17.证明:∵FB=CE,
∴BC=EF,
又∵AB∥ED,AC∥FD,
∴∠ABC=∠DEF,∠ACB=∠DFE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴AC=DF,
在△AOC和△DOF中,
,
∴△AOC≌△DOF(AAS)
∴AO=DO,FO=CO,
∵BF=CE,
∴BO=EO,
∴AD与BE互相平分.
18.【问题解决】证明:在CD上截取CH=CE,如图1所示:
∵△ABC是等边三角形,
∴∠ECH=60°,
∴△CEH是等边三角形,
∴EH=EC=CH,∠CEH=60°,
∵△DEF是等边三角形,
∴DE=FE,∠DEF=60°,
∴∠DEH+∠HEF=∠FEC+∠HEF=60°,
∴∠DEH=∠FEC,
在△DEH和△FEC中,
,
∴△DEH≌△FEC(SAS),
∴DH=CF,
∴CD=CH+DH=CE+CF,
∴CE+CF=CD;
【类比探究】解:线段CE,CF与CD之间的等量关系是FC=CD+CE;理由如下:
∵△ABC是等边三角形,
∴∠A=∠B=60°,
过D作DG∥AB,交AC的延长线于点G,如图2所示:
∵GD∥AB,
∴∠GDC=∠B=60°,∠DGC=∠A=60°,
∴∠GDC=∠DGC=60°,
∴△GCD为等边三角形,
∴DG=CD=CG,∠GDC=60°,
∵△EDF为等边三角形,
∴ED=DF,∠EDF=∠GDC=60°,
∴∠EDG=∠FDC,
在△EGD和△FCD中,
,
∴△EGD≌△FCD(SAS),
∴EG=FC,
∴FC=EG=CG+CE=CD+CE.
19.(1)证明:在△ABC和△DFE中,
∴△ABC≌△DFE(SAS),
∴∠ACE=∠DEF,
∴AC∥DE;
(2)解:∵△ABC≌△DFE,
∴BC=EF,
∴CB﹣EC=EF﹣EC,
∴EB=CF,
∵BF=13,EC=5,
∴EB==4,
∴CB=4+5=9.
20.证明:∵∠ABD=∠ADB,
∴AB=AD,
∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE,
∵在△ABC和△ADE中,
.
∴△ABC≌△ADE(SAS),
∴BC=DE.
21.(1)证明:
∵AC=AD,
∴∠ACD=∠ADC,
又∵∠BCD=∠EDC=90°,
∴∠ACB=∠ADE,
在△ABC和△AED中,
,
∴△ABC≌△AED(SAS);
(2)解:当∠B=140°时,∠E=140°,
又∵∠BCD=∠EDC=90°,
∴五边形ABCDE中,∠BAE=540°﹣140°×2﹣90°×2=80°.
22.(1)证明:∵AD⊥BC,∠ACB=45°,
∴∠ADB=∠CDE=90°,△ADC是等腰直角三角形,
∴AD=CD,∠CAD=∠ACD=45°,
在△ABD与△CED中,,
∴△ABD≌△CED(SAS);
(2)解:∵CE为∠ACD的角平分线,
∴∠ECD=∠ACD=22.5°,
由(1)得:△ABD≌△CED,
∴∠BAD=∠ECD=22.5°,
∴∠BAC=∠BAD+∠CAD=22.5°+45°=67.5°.
23.证明:∵CE∥DF,
∴∠ACE=∠D,
在△ACE和△FDB中,
,
∴△ACE≌△FDB(SAS),
∴AE=FB.
24.证明:∵AB∥CD、EC∥BF,
∴四边形BFCE是平行四边形,∠A=∠D,
∴∠BEC=∠BFC,BE=CF,
∴∠AEG=∠DFH,
∵AB=CD,
∴AE=DF,
在△AEG和△DFH中,
∵,
∴△AEG≌△DFH(ASA),
∴AG=DH.
25.证明:∵AD=BC,∴AC=BD,
在△ACE和△BDF中,,
∴△ACE≌△BDF(SSS)
∴∠A=∠B,
∴AE∥BF;
26.(1)证明:∵△ACB和△DCE都是等腰直角三角形,
∴CD=CE,CA=CB,
∵∠ACB=90°,∠DCE=90°,
∴∠ECD+∠DCB=∠DCB+∠ACB,即∠ECB=∠ACD,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS);
(2)解:∵△ACD≌△BCE,
∴AD=BE,
∵DB=AB=3cm,
∴BE=2×3cm=6cm;
(3)解:BE与AD垂直.理由如下:
∵△ACD≌△BCE,
∴∠1=∠2,
而∠3=∠4,
∴∠EBD=∠ECD=90°,
∴BE⊥AD.
27.证明:∵∠1=∠2,
∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠DAE,
在△ABC和△ADE中
,
∴△ABC≌△ADE,
∴BC=DE.
28.(1)解:△ABF与△CDE全等,理由如下:
∵DE⊥AC,BF⊥AC,
∴∠AFB=∠CED=90°,
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE,
在Rt△ABF和Rt△CDE中,,
∴Rt△ABF≌Rt△CDE(HL);
(2)证明:∵Rt△ABF≌Rt△CDE,
∴BF=DE,
在△DEG和△BFG中,,
∴△DEG≌△BFG(AAS),
∴EG=FG.
三.全等三角形的应用
29.解:∵DE∥AB,
∴∠A=∠E,
在△ABC和△EDC中,
,
∴△ABC≌△EDC(AAS),
∴DE=AB,
即DE的长就是A、B之间的距离.
30.(1)解:河的宽度是5m;
(2)证明:由作法知,BC=DC,∠ABC=∠EDC=90°,
在Rt△ABC和Rt△EDC中,
,
∴Rt△ABC≌Rt△EDC(ASA),
∴AB=ED,
即他们的做法是正确的.
同步能力提升专题训练(附答案)
一.全等三角形的判定
1.如图,AB=DB,∠ABD=∠CBE,①BE=BC,②∠D=∠A,③∠C=∠E,④AC=DE,能使△ABC≌△DBE的条件有( )个.
A.1
B.2
C.3
D.4
2.如图,AB,CD相交于点E,且AB=CD,试添加一个条件使得△ADE≌△CBE.现给出如下五个条件:①∠A=∠C;②∠B=∠D;③AE=CE;④BE=DE;⑤AD=CB.其中符合要求有( )
A.2个
B.3个
C.4个
D.5个
3.如图,已知四边形ABCD中,AB=10厘米,BC=8厘米,CD=12厘米,∠B=∠C,点E为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为
时,能够使△BPE与△CQP全等.
4.如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC与△DEC全等.
5.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.求证:△AEC≌△BED.
6.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.
求证:△ACD≌△CBE.
7.已知:如图AC,BD相交于点O,∠A=∠D,AB=CD,
求证:△AOB≌△DOC.
8.如图,已知在△ABC中,AB=AC,BC=12厘米,点D为AB上一点且BD=8厘米,点P在线段BC上以2厘米/秒的速度由B点向C点运动,设运动时间为t,同时,点Q在线段CA上由C点向A点运动.
(1)用含t的式子表示PC的长为
;
(2)若点Q的运动速度与点P的运动速度相等,当t=2时,三角形BPD与三角形CQP是否全等,请说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,请求出点Q的运动速度是多少时,能够使三角形BPD与三角形CQP全等?
二.全等三角形的判定与性质
9.如图,BP平分∠ABC,D为BP上一点,E,F分别在BA,BC上,且满足DE=DF,若∠BED=140°,则∠BFD的度数是( )
A.40°
B.50°
C.60°
D.70°
10.如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2cm,BE=0.5cm,则DE=
cm.
11.如图,△ABC中,AB=AC,点E,F在边BC上;BE=CF.
(1)求证:△ABE≌△ACF;
(2)若D在AF的延长线上,AD=AC,∠BAE=30°,∠BAD=75°,求证:AB∥DC.
12.如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD所在直线的位置关系为
,线段CF、BD的数量关系为
;
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.
13.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
14.如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,CE⊥BD于点E.
求证:AD=BE.
15.如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD.
16.如图,在△ABC中,AB=AC=8,BC=12,点D从B出发以每秒2个单位的速度在线段BC上从点B向点C运动,点E同时从C出发以每秒2个单位的速度在线段CA上向点A运动,连接AD、DE,设D、E两点运动时间为t秒(0<t<4)
(1)运动
秒时,AE=DC;
(2)运动多少秒时,△ABD≌△DCE能成立,并说明理由;
(3)若△ABD≌△DCE,∠BAC=α,则∠ADE=
(用含α的式子表示).
17.如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,AD交BE于O.求证:AD与BE互相平分.
18.如图,在等边三角形ABC中,点E是边AC上一定点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.
【问题解决】
如图1,若点D在边BC上,求证:CE+CF=CD;
【类比探究】
如图2,若点D在边BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系?并说明理由.
19.如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.
(1)求证:AC∥DE;
(2)若BF=13,EC=5,求BC的长.
20.如图,△ADE的顶点D在△ABC的BC边上,且∠ABD=∠ADB,∠BAD=∠CAE,
求证:BC=DE.
21.如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.
22.如图,在△ABC中,∠ACB=45°,过点A作AD⊥BC于点D,点E为AD上一点,且ED=BD.
(1)求证:△ABD≌△CED;
(2)若CE为∠ACD的角平分线,求∠BAC的度数.
23.如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD.求证:AE=FB.
24.如图,AB∥CD,E、F分别为AB、CD上的点,且EC∥BF,连接AD,分别与EC、BF相交于点G,H,若AB=CD,求证:AG=DH.
25.已知:如图,点A、D、C、B在同一条直线上,AD=BC,AE=BF,CE=DF,求证:AE∥FB.
26.如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰三角形CDE,其中∠DCE=90°,连接BE.
(1)求证:△ACD≌△BCE;
(2)若AB=3cm,则BE=
cm.
(3)BE与AD有何位置关系?请说明理由.
27.如图,已知AB=AD,AC=AE,∠1=∠2,求证:BC=DE.
28.如图所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,垂足分别为E、F,且AB=CD.
(1)△ABF与△CDE全等吗?为什么?
(2)求证:EG=FG.
三.全等三角形的应用
29.如图,A,B两建筑物位于河的两岸,要测它们之间的距离,可以从B点出发在河岸上画一条射线BF,在BF上截取BC=CD,过点D作DE∥AB,使E,C,A在同一直线上,则DE的长就是A,B之间的距离,请你说明道理.
30.某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
①在河流的一条岸边B点,选对岸正对的一棵树A;
②沿河岸直走20m有一树C,继续前行20m到达D处;
③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;
④测得DE的长为5米.
求:(1)河的宽度是多少米?
(2)请你证明他们做法的正确性.
参考答案
一.全等三角形的判定
1.解:∵AB=DB,∠ABD=∠CBE,
∴∠ABC=∠DBE,
∵BE=BC,利用SAS可得△ABC≌△DBE;
∵∠D=∠A,利用ASA可得△ABC≌△DBE;
∵∠C=∠E,利用AAS可得△ABC≌△DBE;
故选:C.
2.解:延长DA、BC使它们相交于点F.
∵∠DAB=∠BCD,∠AED=∠BEC,
∴∠B=∠D,
又∵∠F=∠F,AB=CD,
∴△FAB≌△FCD
∴AF=FC,FD=FB,
∴AD=BC
∴△ADE≌△CBE①对
同理可得②对
∵AE=CE,AB=CD
∴DE=BE
又∵∠AED=∠BEC
∴△ADE≌△CBE(SAS)③对
同理可得④对
连接BD,∵AD=CB,AB=CD,BD=BD,
∴△ADB≌△CBD,
∴∠A=∠C,
∴△ADE≌△CBE,故⑤正确,
故选:D.
3.解:设点P运动的时间为t秒,则BP=3t,CP=8﹣3t,
∵∠B=∠C,
∴①当BE=CP=5,BP=CQ时,△BPE与△CQP全等,
此时,5=8﹣3t,
解得t=1,
∴BP=CQ=3,
此时,点Q的运动速度为3÷1=3厘米/秒;
②当BE=CQ=5,BP=CP时,△BPE与△CQP全等,
此时,3t=8﹣3t,
解得t=,
∴点Q的运动速度为5÷=厘米/秒;
故答案为:3厘米/秒或厘米/秒.
4.解:∵∠BCE=∠ACD=90°,
∴∠3+∠4=∠4+∠5,
∴∠3=∠5,
在△ACD中,∠ACD=90°,
∴∠2+∠D=90°,
∵∠BAE=∠1+∠2=90°,
∴∠1=∠D,
在△ABC和△DEC中,
,
∴△ABC≌△DEC(AAS).
5.证明:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,
∠A=∠B,∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA).
6.证明:∵AD⊥CE,BE⊥CE,
∴∠ADC=∠E=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∵∠B+∠BCE=90°,
∴∠B=∠ACD,
在△BEC和△CDA中,,
∴△ACD≌△CBE(AAS).
7.证明:在△AOB和△DOC中,,
所以,△AOB≌△DOC(AAS).
8.解:(1)BP=2t,则PC=BC﹣BP=12﹣2t;
故答案为(12﹣2t)cm
(2)当t=2时,BP=CQ=2×2=4厘米,
∵BD=8厘米.
又∵PC=BC﹣BP,BC=12厘米,
∴PC=12﹣4=8厘米,
∴PC=BD,
又∵AB=AC,
∴∠B=∠C,
在△BPD和△CQP中,,
∴△BPD≌△CQP(SAS);
③∵vP≠vQ,
∴BP≠CQ,
又∵△BPD≌△CPQ,∠B=∠C,
∴BP=PC=6cm,CQ=BD=8cm,
∴点P,点Q运动的时间t===3秒,
∴VQ==厘米/秒.
即点Q的运动速度是厘米/秒时,能够使三角形BPD与三角形CQP全等.
二.全等三角形的判定与性质
9.解:作DG⊥AB于G,DH⊥BC于H,
∵D是∠ABC平分线上一点,DG⊥AB,DH⊥BC,
∴DH=DG,
在Rt△DEG和Rt△DFH中,
,
∴Rt△DEG≌Rt△DFH(HL),
∴∠DEG=∠DFH,又∠DEG+∠BED=180°,
∴∠BFD+∠BED=180°,
∴∠BFD的度数=180°﹣140°=40°,
故选:A.
10.解:∵BE⊥CE,AD⊥CE
∴∠E=∠ADC=90°
∴∠DAC+∠DCA=90°
∵∠ACB=90°
∴∠BCE+∠DCA=90°
∴∠DAC=∠BCE
在△ACD和△CBE中,
,
∴△ACD≌△CBE
∴BE=CD=0.5(cm),EC=AD=2(cm)
DE=CE﹣CD=1.5(cm),
故答案为1.5
11.证明:∵AB=AC,
∴∠B=∠ACF,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(SAS);
(2)∵△ABE≌△ACF,∠BAE=30°,
∴∠BAE=∠CAF=30°,
∵AD=AC,
∴∠ADC=∠ACD,
∴∠ADC==75°,
∵∠BAD=75°,
∴∠BAD=∠ADC,
∴AB∥DC.
12.证明:(1)①正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
又∵AB=AC,
∴△DAB≌△FAC,
∴CF=BD,∠B=∠ACF,
∴∠ACB+∠ACF=90°,即CF⊥BD.
②当点D在BC的延长线上时①的结论仍成立.
由正方形ADEF得AD=AF,∠DAF=90度.
∵∠BAC=90°,
∴∠DAF=∠BAC,
∴∠DAB=∠FAC,
又∵AB=AC,
∴△DAB≌△FAC,
∴CF=BD,∠ACF=∠ABD.
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∴∠ACF=45°,
∴∠BCF=∠ACB+∠ACF=90度.
即CF⊥BD.
(2)当∠ACB=45°时,CF⊥BD(如图).
理由:过点A作AG⊥AC交CB的延长线于点G,
则∠GAC=90°,
∵∠ACB=45°,∠AGC=90°﹣∠ACB,
∴∠AGC=90°﹣45°=45°,
∴∠ACB=∠AGC=45°,
∴AC=AG,
∵∠DAG=∠FAC(同角的余角相等),AD=AF,
∴△GAD≌△CAF,
∴∠ACF=∠AGC=45°,
∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.
13.解:(1)证明:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,
∠A=∠B,∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA).
(2)∵△AEC≌△BED,
∴EC=ED,∠C=∠BDE.
在△EDC中,
∵EC=ED,∠1=42°,
∴∠C=∠EDC=69°,
∴∠BDE=∠C=69°.
14.证明:∵AD∥BC,
∴∠ADB=∠DBC.
∵CE⊥BD,
∴∠BEC=90°.
∵∠A=90°,
∴∠A=∠BEC.
∵BD=BC,
∴△ABD≌△BCE.
∴AD=BE.
15.证明:∵BD⊥AC于点D,CE⊥AB于点E,
∴∠ADB=∠AEC=90°,
在△ADB和△AEC中,
∴△ADB≌△AEC(ASA)
∴AB=AC,
又∵AD=AE,
∴BE=CD.
16.解:(1)由题可得,BD=CE=2t,
∴CD=12﹣2t,AE=8﹣2t,
∴当AE=DC,时,8﹣2t=(12﹣2t),
解得t=3,
故答案为:3;
(2)当△ABD≌△DCE成立时,AB=CD=8,
∴12﹣2t=8,
解得t=2,
∴运动2秒时,△ABD≌△DCE能成立;
(3)当△ABD≌△DCE时,∠CDE=∠BAD,
又∵∠ADE=180°﹣∠CDE﹣∠ADB,∠B=∠180°﹣∠BAD﹣∠ADB,
∴∠ADE=∠B,
又∵∠BAC=α,AB=AC,
∴∠ADE=∠B=(180°﹣α)=90°﹣α.
故答案为:90°﹣α.
17.证明:∵FB=CE,
∴BC=EF,
又∵AB∥ED,AC∥FD,
∴∠ABC=∠DEF,∠ACB=∠DFE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴AC=DF,
在△AOC和△DOF中,
,
∴△AOC≌△DOF(AAS)
∴AO=DO,FO=CO,
∵BF=CE,
∴BO=EO,
∴AD与BE互相平分.
18.【问题解决】证明:在CD上截取CH=CE,如图1所示:
∵△ABC是等边三角形,
∴∠ECH=60°,
∴△CEH是等边三角形,
∴EH=EC=CH,∠CEH=60°,
∵△DEF是等边三角形,
∴DE=FE,∠DEF=60°,
∴∠DEH+∠HEF=∠FEC+∠HEF=60°,
∴∠DEH=∠FEC,
在△DEH和△FEC中,
,
∴△DEH≌△FEC(SAS),
∴DH=CF,
∴CD=CH+DH=CE+CF,
∴CE+CF=CD;
【类比探究】解:线段CE,CF与CD之间的等量关系是FC=CD+CE;理由如下:
∵△ABC是等边三角形,
∴∠A=∠B=60°,
过D作DG∥AB,交AC的延长线于点G,如图2所示:
∵GD∥AB,
∴∠GDC=∠B=60°,∠DGC=∠A=60°,
∴∠GDC=∠DGC=60°,
∴△GCD为等边三角形,
∴DG=CD=CG,∠GDC=60°,
∵△EDF为等边三角形,
∴ED=DF,∠EDF=∠GDC=60°,
∴∠EDG=∠FDC,
在△EGD和△FCD中,
,
∴△EGD≌△FCD(SAS),
∴EG=FC,
∴FC=EG=CG+CE=CD+CE.
19.(1)证明:在△ABC和△DFE中,
∴△ABC≌△DFE(SAS),
∴∠ACE=∠DEF,
∴AC∥DE;
(2)解:∵△ABC≌△DFE,
∴BC=EF,
∴CB﹣EC=EF﹣EC,
∴EB=CF,
∵BF=13,EC=5,
∴EB==4,
∴CB=4+5=9.
20.证明:∵∠ABD=∠ADB,
∴AB=AD,
∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE,
∵在△ABC和△ADE中,
.
∴△ABC≌△ADE(SAS),
∴BC=DE.
21.(1)证明:
∵AC=AD,
∴∠ACD=∠ADC,
又∵∠BCD=∠EDC=90°,
∴∠ACB=∠ADE,
在△ABC和△AED中,
,
∴△ABC≌△AED(SAS);
(2)解:当∠B=140°时,∠E=140°,
又∵∠BCD=∠EDC=90°,
∴五边形ABCDE中,∠BAE=540°﹣140°×2﹣90°×2=80°.
22.(1)证明:∵AD⊥BC,∠ACB=45°,
∴∠ADB=∠CDE=90°,△ADC是等腰直角三角形,
∴AD=CD,∠CAD=∠ACD=45°,
在△ABD与△CED中,,
∴△ABD≌△CED(SAS);
(2)解:∵CE为∠ACD的角平分线,
∴∠ECD=∠ACD=22.5°,
由(1)得:△ABD≌△CED,
∴∠BAD=∠ECD=22.5°,
∴∠BAC=∠BAD+∠CAD=22.5°+45°=67.5°.
23.证明:∵CE∥DF,
∴∠ACE=∠D,
在△ACE和△FDB中,
,
∴△ACE≌△FDB(SAS),
∴AE=FB.
24.证明:∵AB∥CD、EC∥BF,
∴四边形BFCE是平行四边形,∠A=∠D,
∴∠BEC=∠BFC,BE=CF,
∴∠AEG=∠DFH,
∵AB=CD,
∴AE=DF,
在△AEG和△DFH中,
∵,
∴△AEG≌△DFH(ASA),
∴AG=DH.
25.证明:∵AD=BC,∴AC=BD,
在△ACE和△BDF中,,
∴△ACE≌△BDF(SSS)
∴∠A=∠B,
∴AE∥BF;
26.(1)证明:∵△ACB和△DCE都是等腰直角三角形,
∴CD=CE,CA=CB,
∵∠ACB=90°,∠DCE=90°,
∴∠ECD+∠DCB=∠DCB+∠ACB,即∠ECB=∠ACD,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS);
(2)解:∵△ACD≌△BCE,
∴AD=BE,
∵DB=AB=3cm,
∴BE=2×3cm=6cm;
(3)解:BE与AD垂直.理由如下:
∵△ACD≌△BCE,
∴∠1=∠2,
而∠3=∠4,
∴∠EBD=∠ECD=90°,
∴BE⊥AD.
27.证明:∵∠1=∠2,
∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠DAE,
在△ABC和△ADE中
,
∴△ABC≌△ADE,
∴BC=DE.
28.(1)解:△ABF与△CDE全等,理由如下:
∵DE⊥AC,BF⊥AC,
∴∠AFB=∠CED=90°,
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE,
在Rt△ABF和Rt△CDE中,,
∴Rt△ABF≌Rt△CDE(HL);
(2)证明:∵Rt△ABF≌Rt△CDE,
∴BF=DE,
在△DEG和△BFG中,,
∴△DEG≌△BFG(AAS),
∴EG=FG.
三.全等三角形的应用
29.解:∵DE∥AB,
∴∠A=∠E,
在△ABC和△EDC中,
,
∴△ABC≌△EDC(AAS),
∴DE=AB,
即DE的长就是A、B之间的距离.
30.(1)解:河的宽度是5m;
(2)证明:由作法知,BC=DC,∠ABC=∠EDC=90°,
在Rt△ABC和Rt△EDC中,
,
∴Rt△ABC≌Rt△EDC(ASA),
∴AB=ED,
即他们的做法是正确的.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
