3.1圆 确定圆的条件练习题 2021——2022学年浙教版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 3.1圆 确定圆的条件练习题 2021——2022学年浙教版九年级数学上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 202.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 22:13:46 | ||
图片预览



文档简介
3.1 圆
确定圆的条件
【基础练习】
知识点1 确定圆的条件
1.可以作圆且只可以作一个圆的条件是
( )
A.已知圆心
B.已知半径
C.过三个已知点
D.过不在同一条直线上的三个点
2.平面直角坐标系内的三个点A(1,-3),B(0,-3),C(2,-3), 确定一个圆.(填“能”或“不能”)?
3.已知AB=4
cm,则过点A,B且半径为3
cm的圆有 个.?
4.如图,已知直线l和A,B两点,求作经过A,B两点的圆,且圆心在直线l上.
知识点2 三角形的外接圆
5.小红不小心把家里的一块圆形玻璃打碎了,现需要配制一块同样大小的圆形玻璃,工人师傅在一块如图所示的玻璃残片的边缘描出了点A,B,C,并作出△ABC,则这块圆形玻璃的圆心是
( )
A.AB,AC边上的中线的交点
B.AB,AC边的垂直平分线的交点
C.AB,AC边上的高线所在直线的交点
D.∠BAC与∠ABC的平分线的交点
6.如图1,在4×4的正方形网格中,A,B,C是三个格点,其中每个小正方形的边长均为1,△ABC的外心可能是
( )
图1
A.点M
B.点N
C.点P
D.点Q
7.如图2所示,在5×5的正方形网格中,一条圆弧经过A,B,C三点,
那么这条圆弧所在圆的圆心是
( )
图2
A.点P
B.点Q
C.点R
D.点M
8.[教材作业题第3题变式]
锐角三角形的外心在 ,直角三角形的外心在 ,钝角三角形的外心在 .
?
9.如图3,小明家的房前有一块矩形的空地,空地上有三棵树A,B,C,小明想建一个圆形花坛,使三棵树都在花坛的边上.请你帮小明把花坛位置画出来(用直尺和圆规作图,不写作法,保留作图痕迹).
图3
【能力提升】
10.如图4,△ABC的顶点都在格点上,则△ABC外接圆的圆心坐标是 .?
图4
11.
如图5,点
A,B,C均在6×6的正方形网格格点上,过A,B,C三点的圆除经过A,B,C三点外,还能经过的格点数为 .?
图5
12.已知△ABC的三边长a,b,c满足a2-6a++|c-5|+9=0,则△ABC外接圆的半径是 .?
13.如图6,在等腰三角形ABC中,AB=AC=10,BC=12,求△ABC外接圆的半径.
图6
14.如图7,已知D是△ABC中∠BAC的平分线所在直线上一点,BD⊥AD于点D,过点D作DE∥AC交AB于点E.
求证:点E是过A,B,D三点的圆的圆心.
图7
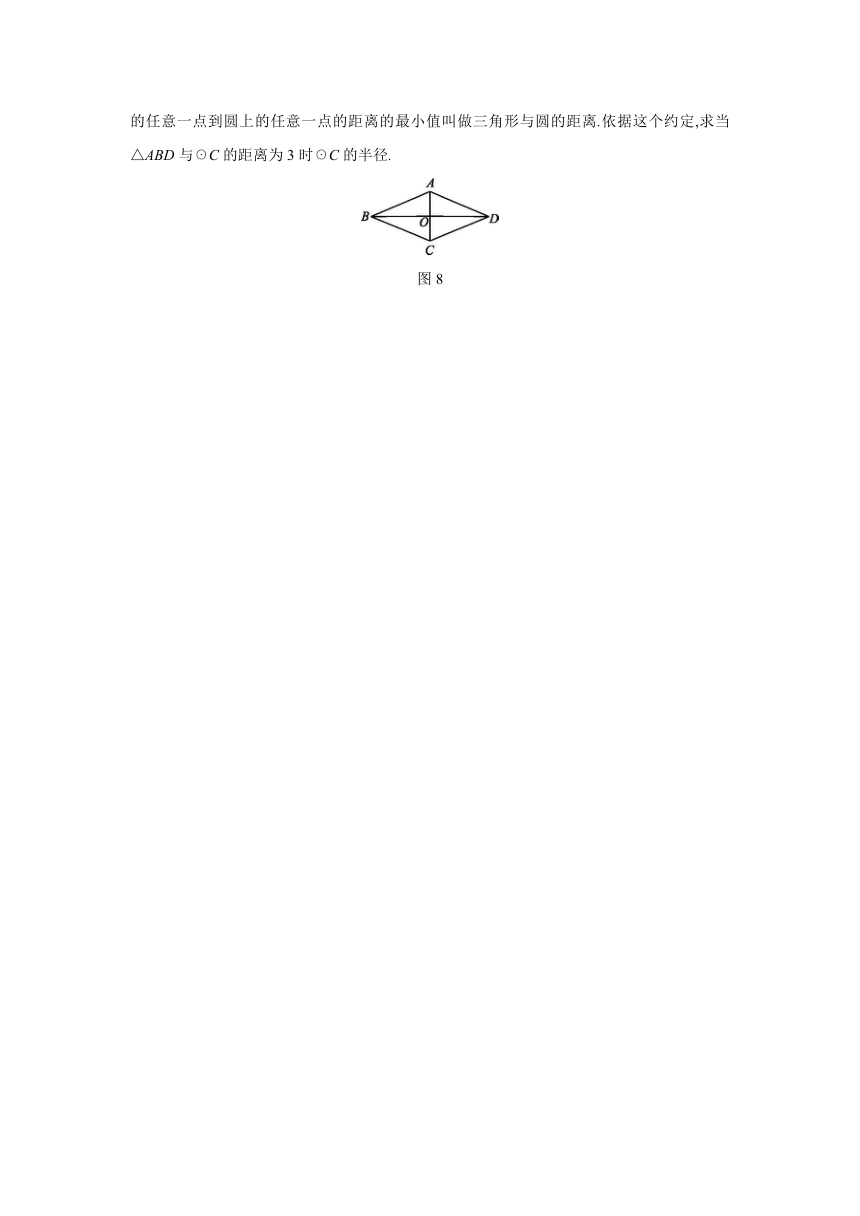
15.如图8,菱形ABCD的边长是13,点O是两条对角线的交点,且OB=12.约定:三角形三边上的任意一点到圆上的任意一点的距离的最小值叫做三角形与圆的距离.依据这个约定,求当△ABD与☉C的距离为3时☉C的半径.
图8
答案
1.D
2.不能 [解析]
因为A,B,C三点在同一条直线上,所以不能确定一个圆.
3.2
4.解:如图,连结AB,作出AB的垂直平分线交直线l于点O,以点O为圆心,OA的长为半径作圆,则☉O即为所求.
5.B [解析]
本题实质上是要确定三角形外接圆的圆心,三角形外接圆的圆心是三边垂直平分线的交点.故选B.
6.D [解析]
由图可知,△ABC是锐角三角形,
所以△ABC的外心只能在其内部,
由此可排除A选项和B选项.
由勾股定理,得BP=CP=≠PA,
所以排除C选项.
故选D.
7.B
8.三角形内 斜边中点上 三角形外
9.解:如图,
连结AB,AC,BC,用尺规作出△ABC任意两边的垂直平分线,交点记为点O,以点O为圆心,OA的长为半径画圆,☉O即为所求作的花坛的位置.
10.(1,2)
11.5 [解析]
如图,分别作AB,BC的中垂线,两直线的交点为O,
以O为圆心,OA为半径作圆,则☉O即为过A,B,C三点的圆.由图可知,☉O还经过点D,E,F,G,H这5个格点.
故答案为5.
12. [解析]
∵a2-6a++|c-5|+9=0,
整理,得(a-3)2++|c-5|=0.
又(a-3)2≥0,≥0,|c-5|≥0,
∴a-3=0且b-4=0且c-5=0,
∴a=3,b=4,c=5,
∴a2+b2=c2,故△ABC是直角三角形,
∴△ABC外接圆的半径r=×5=.
13.解:如图,过点A作AD⊥BC于点D.
∵AB=AC,AD⊥BC,
∴BD=CD.
又∵BC=12,
∴BD=6.
在Rt△ABD中,由勾股定理,得AD==8.
设O为△ABC外接圆的圆心,则点O在AD上,连结BO.
在Rt△BOD中,BO2=OD2+BD2,
即BO2=(8-BO)2+62,
解得BO=,
∴△ABC外接圆的半径为.
14.证明:如图.
∵AD平分∠BAC,
∴∠1=∠2.
∵DE∥AC,
∴∠2=∠3,
∴∠1=∠3,
∴AE=DE.
∵BD⊥AD于点D,
∴∠ADB=90°,
∴∠EBD+∠1=∠EDB+∠3=90°,
∴∠EBD=∠EDB,
∴BE=DE,
∴AE=BE=DE,
∴点E是过A,B,D三点的圆的圆心.
15.解:∵四边形ABCD是菱形,
∴AC⊥BD.
∵菱形ABCD的边长是13,且OB=12,
∴OC===5.
若△ABD中BD边上的中点O到☉C的距离最小,如图①.
∵△ABD与☉C的距离为3,OC=5,
∴☉C的半径为5-3=2.
若菱形ABCD在☉C内,如图②.
∵点B或点D到☉C的距离最小,CD=13,
∴☉C的半径为13+3=16.
综上,当△ABD与☉C的距离为3时,☉C的半径是2或16.
确定圆的条件
【基础练习】
知识点1 确定圆的条件
1.可以作圆且只可以作一个圆的条件是
( )
A.已知圆心
B.已知半径
C.过三个已知点
D.过不在同一条直线上的三个点
2.平面直角坐标系内的三个点A(1,-3),B(0,-3),C(2,-3), 确定一个圆.(填“能”或“不能”)?
3.已知AB=4
cm,则过点A,B且半径为3
cm的圆有 个.?
4.如图,已知直线l和A,B两点,求作经过A,B两点的圆,且圆心在直线l上.
知识点2 三角形的外接圆
5.小红不小心把家里的一块圆形玻璃打碎了,现需要配制一块同样大小的圆形玻璃,工人师傅在一块如图所示的玻璃残片的边缘描出了点A,B,C,并作出△ABC,则这块圆形玻璃的圆心是
( )
A.AB,AC边上的中线的交点
B.AB,AC边的垂直平分线的交点
C.AB,AC边上的高线所在直线的交点
D.∠BAC与∠ABC的平分线的交点
6.如图1,在4×4的正方形网格中,A,B,C是三个格点,其中每个小正方形的边长均为1,△ABC的外心可能是
( )
图1
A.点M
B.点N
C.点P
D.点Q
7.如图2所示,在5×5的正方形网格中,一条圆弧经过A,B,C三点,
那么这条圆弧所在圆的圆心是
( )
图2
A.点P
B.点Q
C.点R
D.点M
8.[教材作业题第3题变式]
锐角三角形的外心在 ,直角三角形的外心在 ,钝角三角形的外心在 .
?
9.如图3,小明家的房前有一块矩形的空地,空地上有三棵树A,B,C,小明想建一个圆形花坛,使三棵树都在花坛的边上.请你帮小明把花坛位置画出来(用直尺和圆规作图,不写作法,保留作图痕迹).
图3
【能力提升】
10.如图4,△ABC的顶点都在格点上,则△ABC外接圆的圆心坐标是 .?
图4
11.
如图5,点
A,B,C均在6×6的正方形网格格点上,过A,B,C三点的圆除经过A,B,C三点外,还能经过的格点数为 .?
图5
12.已知△ABC的三边长a,b,c满足a2-6a++|c-5|+9=0,则△ABC外接圆的半径是 .?
13.如图6,在等腰三角形ABC中,AB=AC=10,BC=12,求△ABC外接圆的半径.
图6
14.如图7,已知D是△ABC中∠BAC的平分线所在直线上一点,BD⊥AD于点D,过点D作DE∥AC交AB于点E.
求证:点E是过A,B,D三点的圆的圆心.
图7
15.如图8,菱形ABCD的边长是13,点O是两条对角线的交点,且OB=12.约定:三角形三边上的任意一点到圆上的任意一点的距离的最小值叫做三角形与圆的距离.依据这个约定,求当△ABD与☉C的距离为3时☉C的半径.
图8
答案
1.D
2.不能 [解析]
因为A,B,C三点在同一条直线上,所以不能确定一个圆.
3.2
4.解:如图,连结AB,作出AB的垂直平分线交直线l于点O,以点O为圆心,OA的长为半径作圆,则☉O即为所求.
5.B [解析]
本题实质上是要确定三角形外接圆的圆心,三角形外接圆的圆心是三边垂直平分线的交点.故选B.
6.D [解析]
由图可知,△ABC是锐角三角形,
所以△ABC的外心只能在其内部,
由此可排除A选项和B选项.
由勾股定理,得BP=CP=≠PA,
所以排除C选项.
故选D.
7.B
8.三角形内 斜边中点上 三角形外
9.解:如图,
连结AB,AC,BC,用尺规作出△ABC任意两边的垂直平分线,交点记为点O,以点O为圆心,OA的长为半径画圆,☉O即为所求作的花坛的位置.
10.(1,2)
11.5 [解析]
如图,分别作AB,BC的中垂线,两直线的交点为O,
以O为圆心,OA为半径作圆,则☉O即为过A,B,C三点的圆.由图可知,☉O还经过点D,E,F,G,H这5个格点.
故答案为5.
12. [解析]
∵a2-6a++|c-5|+9=0,
整理,得(a-3)2++|c-5|=0.
又(a-3)2≥0,≥0,|c-5|≥0,
∴a-3=0且b-4=0且c-5=0,
∴a=3,b=4,c=5,
∴a2+b2=c2,故△ABC是直角三角形,
∴△ABC外接圆的半径r=×5=.
13.解:如图,过点A作AD⊥BC于点D.
∵AB=AC,AD⊥BC,
∴BD=CD.
又∵BC=12,
∴BD=6.
在Rt△ABD中,由勾股定理,得AD==8.
设O为△ABC外接圆的圆心,则点O在AD上,连结BO.
在Rt△BOD中,BO2=OD2+BD2,
即BO2=(8-BO)2+62,
解得BO=,
∴△ABC外接圆的半径为.
14.证明:如图.
∵AD平分∠BAC,
∴∠1=∠2.
∵DE∥AC,
∴∠2=∠3,
∴∠1=∠3,
∴AE=DE.
∵BD⊥AD于点D,
∴∠ADB=90°,
∴∠EBD+∠1=∠EDB+∠3=90°,
∴∠EBD=∠EDB,
∴BE=DE,
∴AE=BE=DE,
∴点E是过A,B,D三点的圆的圆心.
15.解:∵四边形ABCD是菱形,
∴AC⊥BD.
∵菱形ABCD的边长是13,且OB=12,
∴OC===5.
若△ABD中BD边上的中点O到☉C的距离最小,如图①.
∵△ABD与☉C的距离为3,OC=5,
∴☉C的半径为5-3=2.
若菱形ABCD在☉C内,如图②.
∵点B或点D到☉C的距离最小,CD=13,
∴☉C的半径为13+3=16.
综上,当△ABD与☉C的距离为3时,☉C的半径是2或16.
同课章节目录
