3.8弧长及扇形的面积 扇形面积的相关计算练习题 2021—2022学年浙教版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 3.8弧长及扇形的面积 扇形面积的相关计算练习题 2021—2022学年浙教版九年级数学上册(Word版 含答案) | 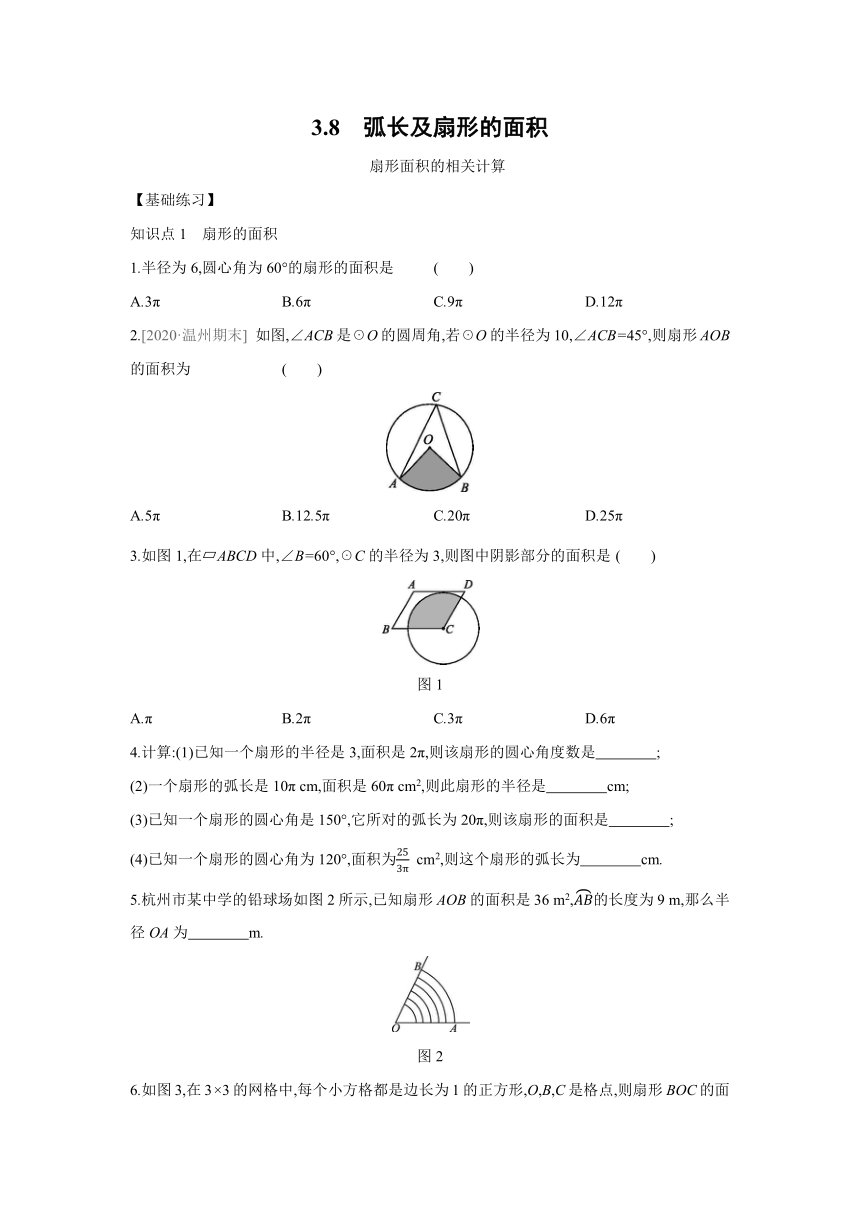 | |
| 格式 | docx | ||
| 文件大小 | 230.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 22:14:52 | ||
图片预览



文档简介
3.8 弧长及扇形的面积
扇形面积的相关计算
【基础练习】
知识点1 扇形的面积
1.半径为6,圆心角为60°的扇形的面积是
( )
A.3π
B.6π
C.9π
D.12π
2.[2020·温州期末]
如图,∠ACB是☉O的圆周角,若☉O的半径为10,∠ACB=45°,则扇形AOB的面积为
( )
A.5π
B.12.5π
C.20π
D.25π
3.如图1,在?ABCD中,∠B=60°,☉C的半径为3,则图中阴影部分的面积是
( )
图1
A.π
B.2π
C.3π
D.6π
4.计算:(1)已知一个扇形的半径是3,面积是2π,则该扇形的圆心角度数是 ;?
(2)一个扇形的弧长是10π
cm,面积是60π
cm2,则此扇形的半径是 cm;?
(3)已知一个扇形的圆心角是150°,它所对的弧长为20π,则该扇形的面积是 ;?
(4)已知一个扇形的圆心角为120°,面积为
cm2,则这个扇形的弧长为 cm.?
5.杭州市某中学的铅球场如图2所示,已知扇形AOB的面积是36
m2,的长度为9
m,那么半径OA为 m.?
图2
6.如图3,在3×3的网格中,每个小方格都是边长为1的正方形,O,B,C是格点,则扇形BOC的面积等于 .(结果保留π)?
图3
知识点2 弓形的面积
7.如图4,一个圆心角为90°的扇形,半径OA=2,那么图中阴影部分的面积为 .(结果保留π)?
图4
8.如图5,AB是☉O的直径,弦AC=2,∠ABC=30°,则图中阴影部分的面积是 .?
图5
9.如图6,小明自制一个乒乓球拍,正面是半径为8
cm的☉O,的度数为90°,在正面弓形ACB(阴影部分)粘贴胶皮,则胶皮的面积为 .?
图6
知识点3 不规则图形的面积
10.
今年寒假期间,小芮参观了中国扇博物馆,如图7是她看到的折扇和团扇.已知折扇的骨柄长为30
cm,扇面的宽度为18
cm,折扇张开的角度为120°.若这两把扇子的扇面面积相等,则团扇的半径为
( )
图7
A.6
cm
B.8
cm
C.6
cm
D.8
cm
11.如图8,AB为☉O的直径,AB=AC,BC交☉O于点D,AC交☉O于点E.
(1)求证:BD=CD;
(2)若AB=8,∠BAC=45°,求图中阴影部分的面积.
图8
【能力提升】
12.如图9,AB是☉O的直径,弦CD⊥AB,∠CDB=30°,CD=2,则图中阴影部分的面积为
( )
图9
A.2π
B.π
C.
D.
13.如图10,将一把三角尺和一把半圆形量角器按图中方式叠放,三角尺一边与量角器的零刻度线所在直线重合,重叠部分的量角器弧()对应的圆心角(∠AOB)为120°,OC的长为2
cm,则三角尺和量角器重叠部分的面积为 cm2.?
图10
14.[2020·嘉兴期末]
如图11,一张扇形纸片AOB,∠AOB=120°,OA=6,将这张扇形纸片折叠,使点A与点O重合,折痕为CD,则图中未重叠部分(即阴影部分)的面积为 .?
图11
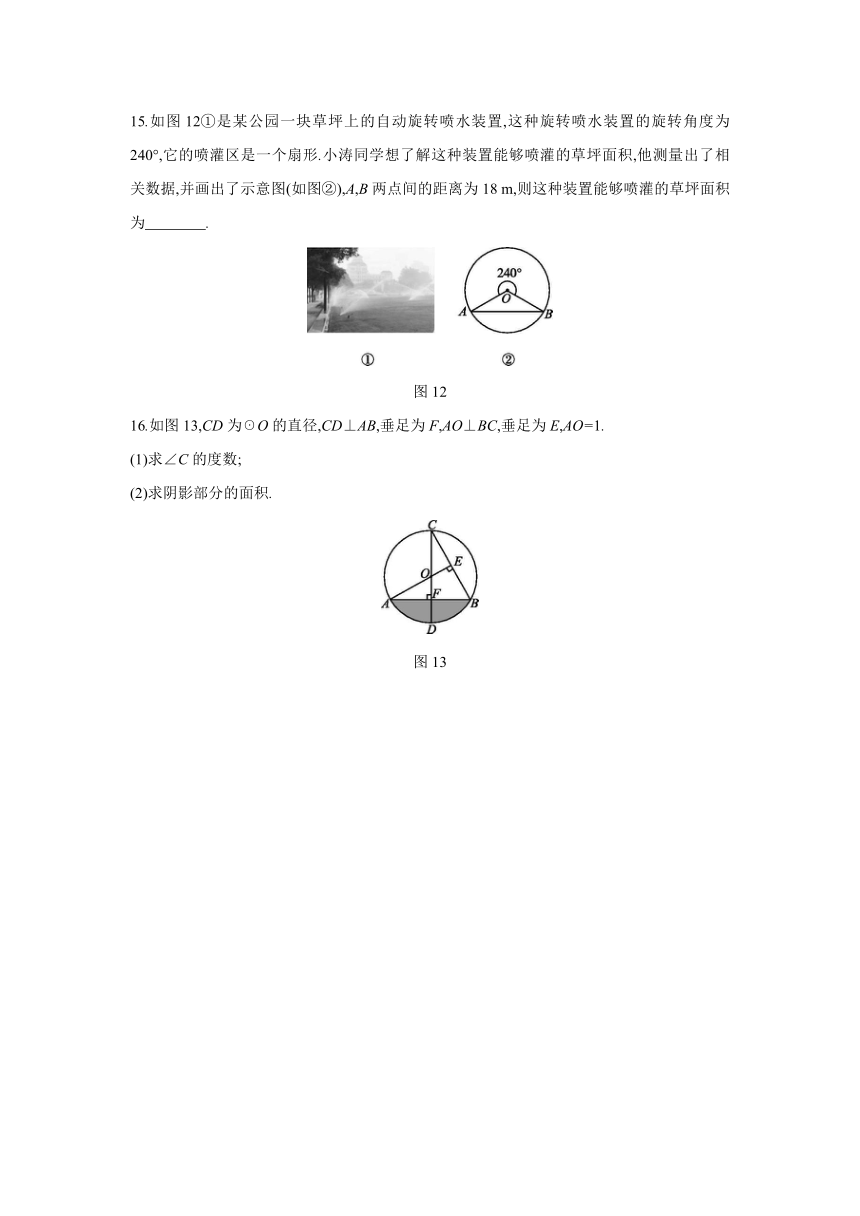
15.如图12①是某公园一块草坪上的自动旋转喷水装置,这种旋转喷水装置的旋转角度为240°,它的喷灌区是一个扇形.小涛同学想了解这种装置能够喷灌的草坪面积,他测量出了相关数据,并画出了示意图(如图②),A,B两点间的距离为18
m,则这种装置能够喷灌的草坪面积为 .?
图12
16.如图13,CD为☉O的直径,CD⊥AB,垂足为F,AO⊥BC,垂足为E,AO=1.
(1)求∠C的度数;
(2)求阴影部分的面积.
图13
答案
1.B 2.D 3.C
4.(1)80° [解析]
根据公式,得=2π,解得n=80.
(2)12
(3)240π [解析]
设扇形的半径为R,
则πR=20π,∴R=24,
∴扇形的面积为×20π×24=240π.
(4) [解析]
∵扇形的圆心角为120°,面积为
cm2,
∴=,∴πR=5,
∴l==
cm,即这个扇形的弧长为
cm.
5.8 [解析]
∵S扇形=lR,∴×9×R=36,
∴R=8.
6.π
7.π-2 [解析]
∵S扇形===π,S△AOB=OA·OB=×2×2=2,
∴阴影部分的面积=S扇形-S△AOB=π-2.
8. [解析]
连结OC,过点C作CH⊥AB于点H.∵AB为☉O的直径,∴∠ACB=90°.∵∠ABC=30°,∴AB=2AC=4,∠AOC=2∠ABC=60°,∴∠BOC=120°,OC=AB=2.
∵CH⊥AB,∴∠OCH=30°,
∴OH=OC=1,
∴CH=,
∴S弓形=S扇形BOC-S△BOC=-OB·CH=-×2×=.
9.(48π+32)cm2 [解析]
如图,连结AO,OB.∵的度数为90°,∴∠AOB=90°,
∴S阴影=S扇形ACB+S△OAB=+×8×8=(48π+32)cm2.
10.A [解析]
设团扇的半径为x
cm.
由题意,得(302-122)=π·x2,
解得x1=6,x2=-6(不合题意,舍去),
∴团扇的半径为6
cm.
故选A.
11.解:(1)证明:如图,连结AD.
∵AB为☉O的直径,
∴∠ADB=90°,即AD⊥BC.
又∵AB=AC,
∴BD=CD.
(2)如图,连结OE.
∵∠BAC=45°,
∴∠BOE=90°,
∴∠AOE=90°.
∵AB=8,
∴OB=OE=4,
∴S阴影=S△BOE+S扇形AOE=×4×4+=8+4π.
12.D [解析]
如图,连结OD,设CD交AB于点E.
∵CD⊥AB,
∴CE=DE=CD=(垂径定理),故S△OCE=S△ODE,
即可得阴影部分的面积等于扇形BOD的面积.
∵∠CDB=30°,
∴∠COB=60°(圆周角定理),∴OC=2.
∵OC=OD,CD⊥OB,
∴∠BOD=∠COB=60°,
∴S扇形BOD==,即阴影部分的面积为.故选D.
13.(π+2) [解析]
∵∠AOB=120°,
∴∠BOC=60°,
∴在Rt△OBC中,∠OBC=30°.
又∵OC=2
cm,∴OB=4
cm,
∴S扇形AOB==π(cm2),BC=2
cm,
∴S△OBC=OC·BC=2
cm2,
∴S重叠=S扇形AOB+S△OBC=π+2cm2.
14.9 [解析]
如图,连结AD,OD.
由折叠可知S弓形AD=S弓形OD,AD=OD.
又∵OA=OD,∴AD=OD=OA,
∴△AOD为等边三角形,
∴∠AOD=60°.
∵∠AOB=120°,
∴∠DOB=60°.
∵AD=OD=OA=6,
∴CO=3,∴CD=3,
∴S弓形AD=S扇形AOD-S△ADO=-×6×3=6π-9,
∴S弓形OD=6π-9,
∴阴影部分的面积=S扇形BOD-S弓形OD=-(6π-9)=9.
15.72π
m2 [解析]
如图,过点O作OC⊥AB于点C.
∵OC⊥AB,AB=18
m,
∴AC=AB=9
m.
∵OA=OB,∠AOB=360°-240°=120°,
∴∠OAB=∠OBA=30°,∴OC=OA.
在Rt△OAC中,OA2=OC2+AC2,AC=9
m,
∴r=OA=6
m,
∴S=πr2=72π(m2).
16.解:(1)如图,连结OB.
∵CD为☉O的直径,CD⊥AB,
∴=,
∴∠AOD=∠BOD=2∠C.
又∵∠AOD=∠COE,∴∠COE=2∠C.
∵AO⊥BC,∴∠OEC=90°,
∴∠C+∠COE=90°,∴3∠C=90°,
∴∠C=30°.
(2)由(1)知∠C=30°,
∴∠AOD=∠BOD=60°,∴∠AOB=120°.
∵在Rt△AOF中,∠AFO=90°,∠AOF=60°,∴∠OAF=30°,
∴OF=AO=,AF=,∴AB=,
∴S阴影=S扇形AOB-S△OAB=×π×12-=π-.
扇形面积的相关计算
【基础练习】
知识点1 扇形的面积
1.半径为6,圆心角为60°的扇形的面积是
( )
A.3π
B.6π
C.9π
D.12π
2.[2020·温州期末]
如图,∠ACB是☉O的圆周角,若☉O的半径为10,∠ACB=45°,则扇形AOB的面积为
( )
A.5π
B.12.5π
C.20π
D.25π
3.如图1,在?ABCD中,∠B=60°,☉C的半径为3,则图中阴影部分的面积是
( )
图1
A.π
B.2π
C.3π
D.6π
4.计算:(1)已知一个扇形的半径是3,面积是2π,则该扇形的圆心角度数是 ;?
(2)一个扇形的弧长是10π
cm,面积是60π
cm2,则此扇形的半径是 cm;?
(3)已知一个扇形的圆心角是150°,它所对的弧长为20π,则该扇形的面积是 ;?
(4)已知一个扇形的圆心角为120°,面积为
cm2,则这个扇形的弧长为 cm.?
5.杭州市某中学的铅球场如图2所示,已知扇形AOB的面积是36
m2,的长度为9
m,那么半径OA为 m.?
图2
6.如图3,在3×3的网格中,每个小方格都是边长为1的正方形,O,B,C是格点,则扇形BOC的面积等于 .(结果保留π)?
图3
知识点2 弓形的面积
7.如图4,一个圆心角为90°的扇形,半径OA=2,那么图中阴影部分的面积为 .(结果保留π)?
图4
8.如图5,AB是☉O的直径,弦AC=2,∠ABC=30°,则图中阴影部分的面积是 .?
图5
9.如图6,小明自制一个乒乓球拍,正面是半径为8
cm的☉O,的度数为90°,在正面弓形ACB(阴影部分)粘贴胶皮,则胶皮的面积为 .?
图6
知识点3 不规则图形的面积
10.
今年寒假期间,小芮参观了中国扇博物馆,如图7是她看到的折扇和团扇.已知折扇的骨柄长为30
cm,扇面的宽度为18
cm,折扇张开的角度为120°.若这两把扇子的扇面面积相等,则团扇的半径为
( )
图7
A.6
cm
B.8
cm
C.6
cm
D.8
cm
11.如图8,AB为☉O的直径,AB=AC,BC交☉O于点D,AC交☉O于点E.
(1)求证:BD=CD;
(2)若AB=8,∠BAC=45°,求图中阴影部分的面积.
图8
【能力提升】
12.如图9,AB是☉O的直径,弦CD⊥AB,∠CDB=30°,CD=2,则图中阴影部分的面积为
( )
图9
A.2π
B.π
C.
D.
13.如图10,将一把三角尺和一把半圆形量角器按图中方式叠放,三角尺一边与量角器的零刻度线所在直线重合,重叠部分的量角器弧()对应的圆心角(∠AOB)为120°,OC的长为2
cm,则三角尺和量角器重叠部分的面积为 cm2.?
图10
14.[2020·嘉兴期末]
如图11,一张扇形纸片AOB,∠AOB=120°,OA=6,将这张扇形纸片折叠,使点A与点O重合,折痕为CD,则图中未重叠部分(即阴影部分)的面积为 .?
图11
15.如图12①是某公园一块草坪上的自动旋转喷水装置,这种旋转喷水装置的旋转角度为240°,它的喷灌区是一个扇形.小涛同学想了解这种装置能够喷灌的草坪面积,他测量出了相关数据,并画出了示意图(如图②),A,B两点间的距离为18
m,则这种装置能够喷灌的草坪面积为 .?
图12
16.如图13,CD为☉O的直径,CD⊥AB,垂足为F,AO⊥BC,垂足为E,AO=1.
(1)求∠C的度数;
(2)求阴影部分的面积.
图13
答案
1.B 2.D 3.C
4.(1)80° [解析]
根据公式,得=2π,解得n=80.
(2)12
(3)240π [解析]
设扇形的半径为R,
则πR=20π,∴R=24,
∴扇形的面积为×20π×24=240π.
(4) [解析]
∵扇形的圆心角为120°,面积为
cm2,
∴=,∴πR=5,
∴l==
cm,即这个扇形的弧长为
cm.
5.8 [解析]
∵S扇形=lR,∴×9×R=36,
∴R=8.
6.π
7.π-2 [解析]
∵S扇形===π,S△AOB=OA·OB=×2×2=2,
∴阴影部分的面积=S扇形-S△AOB=π-2.
8. [解析]
连结OC,过点C作CH⊥AB于点H.∵AB为☉O的直径,∴∠ACB=90°.∵∠ABC=30°,∴AB=2AC=4,∠AOC=2∠ABC=60°,∴∠BOC=120°,OC=AB=2.
∵CH⊥AB,∴∠OCH=30°,
∴OH=OC=1,
∴CH=,
∴S弓形=S扇形BOC-S△BOC=-OB·CH=-×2×=.
9.(48π+32)cm2 [解析]
如图,连结AO,OB.∵的度数为90°,∴∠AOB=90°,
∴S阴影=S扇形ACB+S△OAB=+×8×8=(48π+32)cm2.
10.A [解析]
设团扇的半径为x
cm.
由题意,得(302-122)=π·x2,
解得x1=6,x2=-6(不合题意,舍去),
∴团扇的半径为6
cm.
故选A.
11.解:(1)证明:如图,连结AD.
∵AB为☉O的直径,
∴∠ADB=90°,即AD⊥BC.
又∵AB=AC,
∴BD=CD.
(2)如图,连结OE.
∵∠BAC=45°,
∴∠BOE=90°,
∴∠AOE=90°.
∵AB=8,
∴OB=OE=4,
∴S阴影=S△BOE+S扇形AOE=×4×4+=8+4π.
12.D [解析]
如图,连结OD,设CD交AB于点E.
∵CD⊥AB,
∴CE=DE=CD=(垂径定理),故S△OCE=S△ODE,
即可得阴影部分的面积等于扇形BOD的面积.
∵∠CDB=30°,
∴∠COB=60°(圆周角定理),∴OC=2.
∵OC=OD,CD⊥OB,
∴∠BOD=∠COB=60°,
∴S扇形BOD==,即阴影部分的面积为.故选D.
13.(π+2) [解析]
∵∠AOB=120°,
∴∠BOC=60°,
∴在Rt△OBC中,∠OBC=30°.
又∵OC=2
cm,∴OB=4
cm,
∴S扇形AOB==π(cm2),BC=2
cm,
∴S△OBC=OC·BC=2
cm2,
∴S重叠=S扇形AOB+S△OBC=π+2cm2.
14.9 [解析]
如图,连结AD,OD.
由折叠可知S弓形AD=S弓形OD,AD=OD.
又∵OA=OD,∴AD=OD=OA,
∴△AOD为等边三角形,
∴∠AOD=60°.
∵∠AOB=120°,
∴∠DOB=60°.
∵AD=OD=OA=6,
∴CO=3,∴CD=3,
∴S弓形AD=S扇形AOD-S△ADO=-×6×3=6π-9,
∴S弓形OD=6π-9,
∴阴影部分的面积=S扇形BOD-S弓形OD=-(6π-9)=9.
15.72π
m2 [解析]
如图,过点O作OC⊥AB于点C.
∵OC⊥AB,AB=18
m,
∴AC=AB=9
m.
∵OA=OB,∠AOB=360°-240°=120°,
∴∠OAB=∠OBA=30°,∴OC=OA.
在Rt△OAC中,OA2=OC2+AC2,AC=9
m,
∴r=OA=6
m,
∴S=πr2=72π(m2).
16.解:(1)如图,连结OB.
∵CD为☉O的直径,CD⊥AB,
∴=,
∴∠AOD=∠BOD=2∠C.
又∵∠AOD=∠COE,∴∠COE=2∠C.
∵AO⊥BC,∴∠OEC=90°,
∴∠C+∠COE=90°,∴3∠C=90°,
∴∠C=30°.
(2)由(1)知∠C=30°,
∴∠AOD=∠BOD=60°,∴∠AOB=120°.
∵在Rt△AOF中,∠AFO=90°,∠AOF=60°,∴∠OAF=30°,
∴OF=AO=,AF=,∴AB=,
∴S阴影=S扇形AOB-S△OAB=×π×12-=π-.
同课章节目录
