4.5相似三角形的性质及其应用 相似三角形的性质2(周长、面积的比)练习题 2021—2022学年浙教版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 4.5相似三角形的性质及其应用 相似三角形的性质2(周长、面积的比)练习题 2021—2022学年浙教版九年级数学上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 190.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 22:16:35 | ||
图片预览



文档简介
4.5 相似三角形的性质及其应用
相似三角形的性质2(周长、面积的比)
【基础练习】
知识点1 相似三角形的周长比
1.如图1,AB∥CD,=,则△AOB的周长与△DOC的周长比是 .?
图1
2.已知△ABC∽△A'B'C',相似比为,△ABC的周长为6,则△A'B'C'的周长为 .?
3.如图2,在△ABC中,D,E分别是边AB,AC上的点,且DE∥BC.若△ADE与△ABC的周长之比为2∶3,AD=4,则DB= .?
图2
4.已知两个相似三角形的一对对应边长分别是35
cm和14
cm,且它们的周长相差60
cm,求这两个三角形的周长.
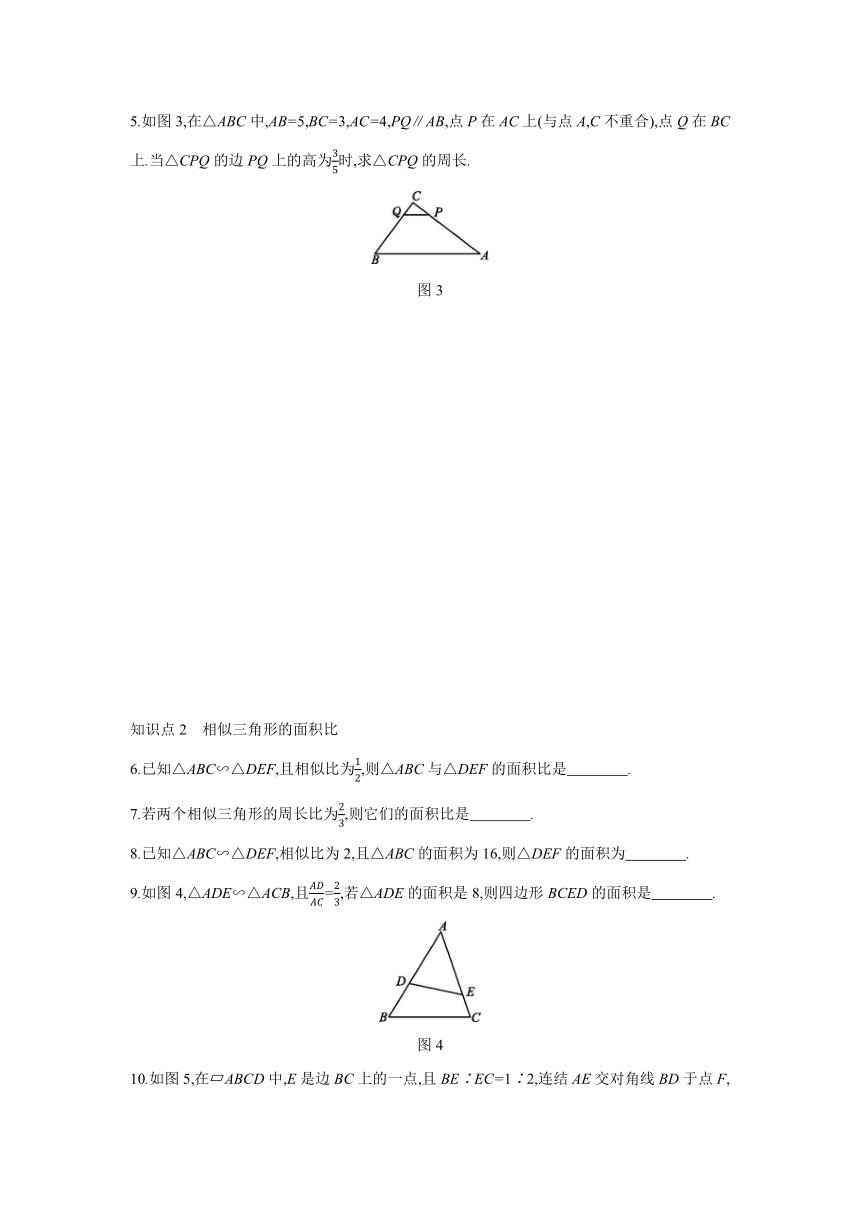
5.如图3,在△ABC中,AB=5,BC=3,AC=4,PQ∥AB,点P在AC上(与点A,C不重合),点Q在BC上.当△CPQ的边PQ上的高为时,求△CPQ的周长.
图3
知识点2 相似三角形的面积比
6.已知△ABC∽△DEF,且相似比为,则△ABC与△DEF的面积比是 .?
7.若两个相似三角形的周长比为,则它们的面积比是 .?
8.已知△ABC∽△DEF,相似比为2,且△ABC的面积为16,则△DEF的面积为 .?
9.如图4,△ADE∽△ACB,且=,若△ADE的面积是8,则四边形BCED的面积是 .?
图4
10.如图5,在?ABCD中,E是边BC上的一点,且BE∶EC=1∶2,连结AE交对角线BD于点F,若S△BFE=12
cm2,求S△DFA.
图5
【能力提升】
11.两个相似三角形的对应角平分线的比是∶1,其中一个三角形的面积为16,则另一个三角形的面积为
( )
A.8或16
B.8或32
C.8
D.8
12.[2020·南通]
如图6,在正方形网格中,每个小正方形的边长均为1,△ABC和△DEF的顶点都在网格线的交点上,设△ABC的周长为C1,△DEF的周长为C2,则的值等于 .?
图6
13.
如图7,在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,EF∥AB,AD∶BD=5∶3,△ABC的面积为64,则四边形BFED的面积为 .?
图7
14.如图8,在△ABC中,中线BE,CD相交于点O,连结DE,下列结论中正确的有 (填序号).?
①=;②=;
③=;④=.
图8
15.[2019·宁波镇海区一模]
在图9所示的6×6的网格中,已知格点三角形ABC(顶点A,B,C都在格点上).
(1)在图?中,画出一个与△ABC面积相等的格点三角形ABD(不与△ABC全等).
(2)在图?中,画出一个与△ABC相似的格点三角形A1B1C1,使得①S△ABC∶=1∶4;②两个三角形的对应边分别互相垂直.
图9
16.[问题背景]
(1)如图10①所示,在△ABC中,DE∥BC,与AB,AC分别交于D,E两点,过点E作EF∥AB交BC于点F.请按图示数据填空:
四边形DBFE的面积S= ,△EFC的面积S1= ,△ADE的面积S2= .?
[探究发现]
(2)在(1)中,若BF=a,FC=b,DE与BC间的距离为h,请证明S2=4S1S2.
[拓展迁移]
(3)如图10②,?DEFG的四个顶点在△ABC的三边上,若△ADG,△DBE,△GFC的面积分别为2,5,3,试利用(2)中的结论求△ABC的面积.
图10
答案
1. 2.8 3.2
4.解:∵两个相似三角形的一对对应边长分别是35
cm和14
cm,
∴这两个相似三角形的相似比为5∶2,
∴这两个相似三角形的周长比为5∶2.
设较大的三角形的周长为5x
cm,则较小的三角形的周长为2x
cm.
∵它们的周长相差60
cm,
∴5x-2x=60,解得x=20,
∴5x=5×20=100,2x=2×20=40,
∴较大的三角形的周长为100
cm,较小的三角形的周长为40
cm.
5.解:∵AB=5,BC=3,AC=4,
∴AB2=AC2+BC2,
∴△ABC为直角三角形,其斜边AB上的高为=.
∵PQ∥AB,
∴△CPQ∽△CAB,相似比==,
∴=.
∵△CAB的周长=3+4+5=12,
∴△CPQ的周长=×12=3.
6. 7.
8.4 [解析]
∵△ABC∽△DEF,相似比为2,
∴△ABC和△DEF的面积比为4.
∵△ABC的面积为16,∴△DEF的面积为4.
9.10 [解析]
∵△ADE∽△ACB,且=,
∴=,即=,
解得S△ABC=18,
∴S四边形BCED=18-8=10.
10.解:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∵BE∶EC=1∶2,
∴BE∶BC=1∶3,即BE∶AD=1∶3.
∵AD∥BC,∴△BFE∽△DFA,
∴S△BFE∶S△DFA=(BE∶AD)2=1∶9.
∵S△BFE=12
cm2,∴S△DFA=108
cm2.
11.B [解析]
设两个三角形的面积分别是S1,S2,令S1=16.
①若=2,有=,∴S2=8;
②若=2,有=,∴S2=32.
故选B.
12.
13.30
14.①③④ [解析]
①∵DE是△ABC的中位线,
∴DE=BC,即=,
故①正确;
②∵DE是△ABC的中位线,∴DE∥BC,
∴△DOE∽△COB,
∴===,
故②错误;
③∵DE∥BC,
∴△ADE∽△ABC,△DOE∽△COB,
∴=,=,∴=,
故③正确;
④∵△ABC的中线BE与CD相交于点O,
∴点O是△ABC的重心,
根据重心性质,可得BO=2OE,△ABC的高=3△COB的高,且△ABC与△COB同底(BC),
∴S△ABC=3S△OBC.
由②和③知,
S△DOE=S△COB,S△ADE=S△ABC,
∴S△ADE=S△COB,∴=,
故④正确.
综上,①③④正确.
15.解:(1)如图①,△ABD为所作.(答案不唯一)
(2)如图②,△A1B1C1为所作.
16.解:(1)6 9 1
(2)证明:∵DE∥BC,EF∥AB,
∴四边形DBFE为平行四边形,∠AED=∠C,∠A=∠CEF,
∴DE=BF=a,△ADE∽△EFC,
∴=2=.
∵S1=bh,
∴S2=·S1=,
∴4S1S2=4·bh·=(ah)2.
而S=ah,∴S2=4S1S2.
(3)过点G作GH∥AB交BC于点H,则四边形DBHG为平行四边形,
∴∠GHC=∠B,BD=GH,DG=BH.
∵四边形DEFG为平行四边形,
∴DG=EF,∴BH=EF,
∴BE=HF,∴△DBE≌△GHF,
∴△GHC的面积为5+3=8.
由(2)得?DBHG的面积为=8,
∴△ABC的面积为2+8+8=18.
相似三角形的性质2(周长、面积的比)
【基础练习】
知识点1 相似三角形的周长比
1.如图1,AB∥CD,=,则△AOB的周长与△DOC的周长比是 .?
图1
2.已知△ABC∽△A'B'C',相似比为,△ABC的周长为6,则△A'B'C'的周长为 .?
3.如图2,在△ABC中,D,E分别是边AB,AC上的点,且DE∥BC.若△ADE与△ABC的周长之比为2∶3,AD=4,则DB= .?
图2
4.已知两个相似三角形的一对对应边长分别是35
cm和14
cm,且它们的周长相差60
cm,求这两个三角形的周长.
5.如图3,在△ABC中,AB=5,BC=3,AC=4,PQ∥AB,点P在AC上(与点A,C不重合),点Q在BC上.当△CPQ的边PQ上的高为时,求△CPQ的周长.
图3
知识点2 相似三角形的面积比
6.已知△ABC∽△DEF,且相似比为,则△ABC与△DEF的面积比是 .?
7.若两个相似三角形的周长比为,则它们的面积比是 .?
8.已知△ABC∽△DEF,相似比为2,且△ABC的面积为16,则△DEF的面积为 .?
9.如图4,△ADE∽△ACB,且=,若△ADE的面积是8,则四边形BCED的面积是 .?
图4
10.如图5,在?ABCD中,E是边BC上的一点,且BE∶EC=1∶2,连结AE交对角线BD于点F,若S△BFE=12
cm2,求S△DFA.
图5
【能力提升】
11.两个相似三角形的对应角平分线的比是∶1,其中一个三角形的面积为16,则另一个三角形的面积为
( )
A.8或16
B.8或32
C.8
D.8
12.[2020·南通]
如图6,在正方形网格中,每个小正方形的边长均为1,△ABC和△DEF的顶点都在网格线的交点上,设△ABC的周长为C1,△DEF的周长为C2,则的值等于 .?
图6
13.
如图7,在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,EF∥AB,AD∶BD=5∶3,△ABC的面积为64,则四边形BFED的面积为 .?
图7
14.如图8,在△ABC中,中线BE,CD相交于点O,连结DE,下列结论中正确的有 (填序号).?
①=;②=;
③=;④=.
图8
15.[2019·宁波镇海区一模]
在图9所示的6×6的网格中,已知格点三角形ABC(顶点A,B,C都在格点上).
(1)在图?中,画出一个与△ABC面积相等的格点三角形ABD(不与△ABC全等).
(2)在图?中,画出一个与△ABC相似的格点三角形A1B1C1,使得①S△ABC∶=1∶4;②两个三角形的对应边分别互相垂直.
图9
16.[问题背景]
(1)如图10①所示,在△ABC中,DE∥BC,与AB,AC分别交于D,E两点,过点E作EF∥AB交BC于点F.请按图示数据填空:
四边形DBFE的面积S= ,△EFC的面积S1= ,△ADE的面积S2= .?
[探究发现]
(2)在(1)中,若BF=a,FC=b,DE与BC间的距离为h,请证明S2=4S1S2.
[拓展迁移]
(3)如图10②,?DEFG的四个顶点在△ABC的三边上,若△ADG,△DBE,△GFC的面积分别为2,5,3,试利用(2)中的结论求△ABC的面积.
图10
答案
1. 2.8 3.2
4.解:∵两个相似三角形的一对对应边长分别是35
cm和14
cm,
∴这两个相似三角形的相似比为5∶2,
∴这两个相似三角形的周长比为5∶2.
设较大的三角形的周长为5x
cm,则较小的三角形的周长为2x
cm.
∵它们的周长相差60
cm,
∴5x-2x=60,解得x=20,
∴5x=5×20=100,2x=2×20=40,
∴较大的三角形的周长为100
cm,较小的三角形的周长为40
cm.
5.解:∵AB=5,BC=3,AC=4,
∴AB2=AC2+BC2,
∴△ABC为直角三角形,其斜边AB上的高为=.
∵PQ∥AB,
∴△CPQ∽△CAB,相似比==,
∴=.
∵△CAB的周长=3+4+5=12,
∴△CPQ的周长=×12=3.
6. 7.
8.4 [解析]
∵△ABC∽△DEF,相似比为2,
∴△ABC和△DEF的面积比为4.
∵△ABC的面积为16,∴△DEF的面积为4.
9.10 [解析]
∵△ADE∽△ACB,且=,
∴=,即=,
解得S△ABC=18,
∴S四边形BCED=18-8=10.
10.解:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∵BE∶EC=1∶2,
∴BE∶BC=1∶3,即BE∶AD=1∶3.
∵AD∥BC,∴△BFE∽△DFA,
∴S△BFE∶S△DFA=(BE∶AD)2=1∶9.
∵S△BFE=12
cm2,∴S△DFA=108
cm2.
11.B [解析]
设两个三角形的面积分别是S1,S2,令S1=16.
①若=2,有=,∴S2=8;
②若=2,有=,∴S2=32.
故选B.
12.
13.30
14.①③④ [解析]
①∵DE是△ABC的中位线,
∴DE=BC,即=,
故①正确;
②∵DE是△ABC的中位线,∴DE∥BC,
∴△DOE∽△COB,
∴===,
故②错误;
③∵DE∥BC,
∴△ADE∽△ABC,△DOE∽△COB,
∴=,=,∴=,
故③正确;
④∵△ABC的中线BE与CD相交于点O,
∴点O是△ABC的重心,
根据重心性质,可得BO=2OE,△ABC的高=3△COB的高,且△ABC与△COB同底(BC),
∴S△ABC=3S△OBC.
由②和③知,
S△DOE=S△COB,S△ADE=S△ABC,
∴S△ADE=S△COB,∴=,
故④正确.
综上,①③④正确.
15.解:(1)如图①,△ABD为所作.(答案不唯一)
(2)如图②,△A1B1C1为所作.
16.解:(1)6 9 1
(2)证明:∵DE∥BC,EF∥AB,
∴四边形DBFE为平行四边形,∠AED=∠C,∠A=∠CEF,
∴DE=BF=a,△ADE∽△EFC,
∴=2=.
∵S1=bh,
∴S2=·S1=,
∴4S1S2=4·bh·=(ah)2.
而S=ah,∴S2=4S1S2.
(3)过点G作GH∥AB交BC于点H,则四边形DBHG为平行四边形,
∴∠GHC=∠B,BD=GH,DG=BH.
∵四边形DEFG为平行四边形,
∴DG=EF,∴BH=EF,
∴BE=HF,∴△DBE≌△GHF,
∴△GHC的面积为5+3=8.
由(2)得?DBHG的面积为=8,
∴△ABC的面积为2+8+8=18.
同课章节目录
