第一章 二次函数 题型分类汇总练习(一)2021-2022学年九年级数学浙教版上册(Word版 含答案)
文档属性
| 名称 | 第一章 二次函数 题型分类汇总练习(一)2021-2022学年九年级数学浙教版上册(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 247.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 00:00:00 | ||
图片预览



文档简介
二次函数经典题型分类汇总练习
类型一、二次函数的基本概念
1.下列各式中,是二次函数的是(
)
A.
B.
C.
D.
2.(2020·苏州市平江中学校九年级期中)二次函数的图象经过原点,则__________.
3.(2021·安徽九年级期末)二次函数的二次项系数与常数项的和是__________.
4.(2021·河南九年级模拟)若函数是关于x的二次函数,则m的值是(
)
A.2
B.或3
C.3
D.
类型二、二次函数的图像及其性质
5.关于二次函数的图象,下列说法正确的是(
)
A.开口向上
B.最低点是
C.可以由向左平移2个单位得到
D.当时,随的增大而增大
6.(2021·山东烟台市·九年级期末)下列函数中,当x>0时,y随x的增大而减小的是(
)
A.y=x2
B.y=x﹣1
C.y=
D.y=﹣x2
1.坐标系中图像判断
7.二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax-b的图象大致是( )
A.
B.
C.
D.
8.(桐乡九上期中)二次函数y=ax2+bx+c的图象如图所示,则反比例函数与一次函数y=bx+c在同一坐标系中的大致图象是(
)
A.
B.
C.
D.
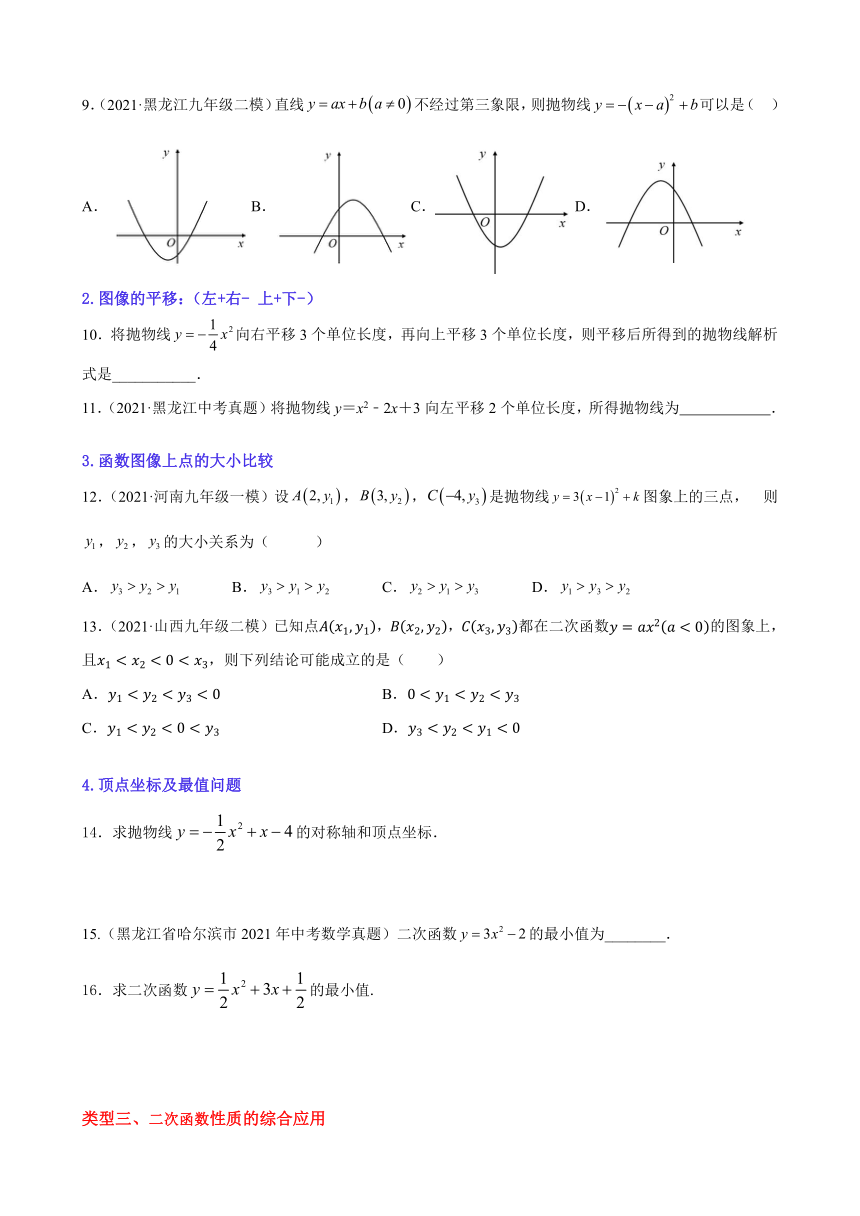
9.(2021·黑龙江九年级二模)直线不经过第三象限,则抛物线可以是(
)
A.B.C.D.
2.图像的平移:(左+右-
上+下-)
10.将抛物线向右平移3个单位长度,再向上平移3个单位长度,则平移后所得到的抛物线解析式是___________.
11.(2021·黑龙江中考真题)将抛物线y=x2﹣2x+3向左平移2个单位长度,所得抛物线为
.
3.函数图像上点的大小比较
12.(2021·河南九年级一模)设,,是抛物线图象上的三点,
则,,的大小关系为(
)
A.
B.
C.
D.
13.(2021·山西九年级二模)已知点,,都在二次函数的图象上,且,则下列结论可能成立的是(
)
A.
B.
C.
D.
4.顶点坐标及最值问题
14.求抛物线的对称轴和顶点坐标.
15.(黑龙江省哈尔滨市2021年中考数学真题)二次函数的最小值为________.
16.求二次函数的最小值.
类型三、二次函数性质的综合应用
1.图像的综合应用
17.(2019·湖北九年级期中)在平面直角坐标系中,二次函数的图象如图所示,下列结论:①;②;③;④a-b+c<0.其中正确结论的个数是(
)
A.1个
B.2个
C.3个
D.4个
18.(2021·吉林东北师大附中)已知二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图象如图所示,下面四个结论,①abc<0;②a+c<b;③2a+b=1;④a+b≥m(am+b),其中全部正确的是______
2.用待定系数法求函数解析式
19.已知:抛物线经过A(0,),B(1,),C(,)三点
求它的顶点坐标及对称轴.
20.(2020·江西宜春九中)已知二次函数的顶点为且过点,求该函数解析式.
21.已知抛物线经过(3,5),A(4,0),B(-2,0),且与y轴交于点C.
(1)求二次函数解析式;
(2)求△ABC的面积.
3.二次函数与实际问题
22.(2020·上海市静安区实验中学)在半径为4cm
的圆中,挖去了一个半径为xcm的圆面,剩下一个圆环的面积为ycm2,则y与x的函数关系式为(
)
A.
B.
C.
D.
23.(2020·德庆县九市中学九年级月考)如图,二次函数y=﹣x2+(k﹣1)x+4的图象与y轴交于点A,与x轴的负半轴交于点B,且△AOB的面积为6.
(1)求A,B两点的坐标;
(2)求该二次函数的表达式;
(3)如果点P在坐标轴上,且△ABP是等腰三角形,求点P的坐标.
24.进价为每件40元的某商品,售价为每件50元时,每星期可卖出500件,市场调查反映:如果每件的售价每降价1元,每星期可多卖出100件,但售价不能低于每件42元,且每星期至少要销售800件.设每件降价x元
(x为正整数),每星期的利润为y元.
(1)求y与x的函数关系式并写出自变量x的取值范围;
(2)若某星期的利润为5600元,此利润是否是该星期的最大利润?说明理由.
(3)直接写出售价为多少时,每星期的利润不低于5000元?
【参考答案】
C
2,3
3,1
4,C
D
6,D
7,B
8,D
9,D
10.
11.y=x2+2x+3
12.A
13.A
14,
顶点坐标为,对称轴为直线.
15.0
16,
y有最小值-4
17.B
18.①②④.
19.设(a≠0),据题意列,解得,
所得函数为
对称轴方程:,顶点.
20.
解:由顶点(-2,2),可设抛物线为:,
将点(-1,3)代入上式可得:
综上所述:.
21.(1)设抛物线解析式为(a≠0),将(3,5)代入得,
∴
.
∴
.
即.
(2)由(1)知C(0,8),
∴
.
22.A
解:圆的面积公式是,
原来的圆的面积=,
挖去的圆的面积=,
∴圆环面积.
23.(1)A的坐标为(0,4),B的坐标为(﹣3,0);(2);(3)点P的坐标为(3,0),(2,0),(﹣8,0),(,0)或(0,)或(0,9)或(0,﹣1)或(0,﹣4).
解:(1)令x=0,y=4,
∴点A的坐标为(0,4),
∵S△OAB=×BO×4=6,
∴BO=3.
∴B(3,0)或(﹣3,0),
∵二次函数与x轴的负半轴交于点B,
∴点B的坐标为(﹣3,0);
(2)把点B的坐标(﹣3,0)代入y=﹣x2+(k﹣1)x+4,
得﹣(﹣3)2+(k﹣1)×(﹣3)+4=0.
解得k﹣1=﹣,
∴所求二次函数的解析式为y=﹣x2﹣x+4;
(3)(Ⅰ)当点P在x轴上时,
①如图1,当AB=AP时,
则点P和点B关于y轴对称,
则点P的坐标为(3,0);
②如图2,当AB=BP时,
当点P在y轴左侧时,BP=AB=5,则OP=PB+OB=5+3=8,故点P(﹣8,0),
当点P在y轴右侧时,则B
=5,则O=B+OB=5﹣3=2,
故点(2,0),
故点P的坐标为(2,0)或(﹣8,0);
③如图3,当AP=BP时,
设点P的坐标为(x,0),
根据题意,得=|x+3|.
解得x=.
∴点P的坐标为(,0);
故点P的坐标为(3,0),(2,0),(﹣8,0),(,0).
(Ⅱ)当点P在y轴上时,
①如图4,当AB=AP时,
∵AB=5,
∴AP=5,
若点P在y轴的正半轴上,OP=AO+AP=9,
则点P的坐标为(0,9);
若点P在y轴的负半轴上,OP=AP-AO=1,
则点P的坐标为(0,-1);
②如图5,当AB=BP时,
又∵BO⊥AP,
∴OP=OA=4,
∴点P的坐标为(0,﹣4);
③如图6,当AP=BP时,
设点P的坐标为(0,y),
根据题意,得=|4-y
|.
解得y=.
∴点P的坐标为(0,)
综上所述,点P的坐标为(3,0),(2,0),(﹣8,0),(,0)或(0,)或(0,9)或(0,﹣1)或(0,﹣4).
24.
解:(1)依题意,得y=(50﹣40﹣x)?(500+100x)=﹣100x2+500x+5000,
∵,
∴3≤x≤8;
(2)y=﹣100x2+500x+5000=﹣100(x﹣)+5625,
∵5600<5625,
∴5600不是最大利润.
(3)当y=5000时,y=﹣100x2+500x+5000=5000,
解得x1=0,x2=5,
故当0≤x≤5时,y≥5000,
即当售价在不小于45元且不大于50元时,月利润不低于5000
类型一、二次函数的基本概念
1.下列各式中,是二次函数的是(
)
A.
B.
C.
D.
2.(2020·苏州市平江中学校九年级期中)二次函数的图象经过原点,则__________.
3.(2021·安徽九年级期末)二次函数的二次项系数与常数项的和是__________.
4.(2021·河南九年级模拟)若函数是关于x的二次函数,则m的值是(
)
A.2
B.或3
C.3
D.
类型二、二次函数的图像及其性质
5.关于二次函数的图象,下列说法正确的是(
)
A.开口向上
B.最低点是
C.可以由向左平移2个单位得到
D.当时,随的增大而增大
6.(2021·山东烟台市·九年级期末)下列函数中,当x>0时,y随x的增大而减小的是(
)
A.y=x2
B.y=x﹣1
C.y=
D.y=﹣x2
1.坐标系中图像判断
7.二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax-b的图象大致是( )
A.
B.
C.
D.
8.(桐乡九上期中)二次函数y=ax2+bx+c的图象如图所示,则反比例函数与一次函数y=bx+c在同一坐标系中的大致图象是(
)
A.
B.
C.
D.
9.(2021·黑龙江九年级二模)直线不经过第三象限,则抛物线可以是(
)
A.B.C.D.
2.图像的平移:(左+右-
上+下-)
10.将抛物线向右平移3个单位长度,再向上平移3个单位长度,则平移后所得到的抛物线解析式是___________.
11.(2021·黑龙江中考真题)将抛物线y=x2﹣2x+3向左平移2个单位长度,所得抛物线为
.
3.函数图像上点的大小比较
12.(2021·河南九年级一模)设,,是抛物线图象上的三点,
则,,的大小关系为(
)
A.
B.
C.
D.
13.(2021·山西九年级二模)已知点,,都在二次函数的图象上,且,则下列结论可能成立的是(
)
A.
B.
C.
D.
4.顶点坐标及最值问题
14.求抛物线的对称轴和顶点坐标.
15.(黑龙江省哈尔滨市2021年中考数学真题)二次函数的最小值为________.
16.求二次函数的最小值.
类型三、二次函数性质的综合应用
1.图像的综合应用
17.(2019·湖北九年级期中)在平面直角坐标系中,二次函数的图象如图所示,下列结论:①;②;③;④a-b+c<0.其中正确结论的个数是(
)
A.1个
B.2个
C.3个
D.4个
18.(2021·吉林东北师大附中)已知二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图象如图所示,下面四个结论,①abc<0;②a+c<b;③2a+b=1;④a+b≥m(am+b),其中全部正确的是______
2.用待定系数法求函数解析式
19.已知:抛物线经过A(0,),B(1,),C(,)三点
求它的顶点坐标及对称轴.
20.(2020·江西宜春九中)已知二次函数的顶点为且过点,求该函数解析式.
21.已知抛物线经过(3,5),A(4,0),B(-2,0),且与y轴交于点C.
(1)求二次函数解析式;
(2)求△ABC的面积.
3.二次函数与实际问题
22.(2020·上海市静安区实验中学)在半径为4cm
的圆中,挖去了一个半径为xcm的圆面,剩下一个圆环的面积为ycm2,则y与x的函数关系式为(
)
A.
B.
C.
D.
23.(2020·德庆县九市中学九年级月考)如图,二次函数y=﹣x2+(k﹣1)x+4的图象与y轴交于点A,与x轴的负半轴交于点B,且△AOB的面积为6.
(1)求A,B两点的坐标;
(2)求该二次函数的表达式;
(3)如果点P在坐标轴上,且△ABP是等腰三角形,求点P的坐标.
24.进价为每件40元的某商品,售价为每件50元时,每星期可卖出500件,市场调查反映:如果每件的售价每降价1元,每星期可多卖出100件,但售价不能低于每件42元,且每星期至少要销售800件.设每件降价x元
(x为正整数),每星期的利润为y元.
(1)求y与x的函数关系式并写出自变量x的取值范围;
(2)若某星期的利润为5600元,此利润是否是该星期的最大利润?说明理由.
(3)直接写出售价为多少时,每星期的利润不低于5000元?
【参考答案】
C
2,3
3,1
4,C
D
6,D
7,B
8,D
9,D
10.
11.y=x2+2x+3
12.A
13.A
14,
顶点坐标为,对称轴为直线.
15.0
16,
y有最小值-4
17.B
18.①②④.
19.设(a≠0),据题意列,解得,
所得函数为
对称轴方程:,顶点.
20.
解:由顶点(-2,2),可设抛物线为:,
将点(-1,3)代入上式可得:
综上所述:.
21.(1)设抛物线解析式为(a≠0),将(3,5)代入得,
∴
.
∴
.
即.
(2)由(1)知C(0,8),
∴
.
22.A
解:圆的面积公式是,
原来的圆的面积=,
挖去的圆的面积=,
∴圆环面积.
23.(1)A的坐标为(0,4),B的坐标为(﹣3,0);(2);(3)点P的坐标为(3,0),(2,0),(﹣8,0),(,0)或(0,)或(0,9)或(0,﹣1)或(0,﹣4).
解:(1)令x=0,y=4,
∴点A的坐标为(0,4),
∵S△OAB=×BO×4=6,
∴BO=3.
∴B(3,0)或(﹣3,0),
∵二次函数与x轴的负半轴交于点B,
∴点B的坐标为(﹣3,0);
(2)把点B的坐标(﹣3,0)代入y=﹣x2+(k﹣1)x+4,
得﹣(﹣3)2+(k﹣1)×(﹣3)+4=0.
解得k﹣1=﹣,
∴所求二次函数的解析式为y=﹣x2﹣x+4;
(3)(Ⅰ)当点P在x轴上时,
①如图1,当AB=AP时,
则点P和点B关于y轴对称,
则点P的坐标为(3,0);
②如图2,当AB=BP时,
当点P在y轴左侧时,BP=AB=5,则OP=PB+OB=5+3=8,故点P(﹣8,0),
当点P在y轴右侧时,则B
=5,则O=B+OB=5﹣3=2,
故点(2,0),
故点P的坐标为(2,0)或(﹣8,0);
③如图3,当AP=BP时,
设点P的坐标为(x,0),
根据题意,得=|x+3|.
解得x=.
∴点P的坐标为(,0);
故点P的坐标为(3,0),(2,0),(﹣8,0),(,0).
(Ⅱ)当点P在y轴上时,
①如图4,当AB=AP时,
∵AB=5,
∴AP=5,
若点P在y轴的正半轴上,OP=AO+AP=9,
则点P的坐标为(0,9);
若点P在y轴的负半轴上,OP=AP-AO=1,
则点P的坐标为(0,-1);
②如图5,当AB=BP时,
又∵BO⊥AP,
∴OP=OA=4,
∴点P的坐标为(0,﹣4);
③如图6,当AP=BP时,
设点P的坐标为(0,y),
根据题意,得=|4-y
|.
解得y=.
∴点P的坐标为(0,)
综上所述,点P的坐标为(3,0),(2,0),(﹣8,0),(,0)或(0,)或(0,9)或(0,﹣1)或(0,﹣4).
24.
解:(1)依题意,得y=(50﹣40﹣x)?(500+100x)=﹣100x2+500x+5000,
∵,
∴3≤x≤8;
(2)y=﹣100x2+500x+5000=﹣100(x﹣)+5625,
∵5600<5625,
∴5600不是最大利润.
(3)当y=5000时,y=﹣100x2+500x+5000=5000,
解得x1=0,x2=5,
故当0≤x≤5时,y≥5000,
即当售价在不小于45元且不大于50元时,月利润不低于5000
同课章节目录
