第3章 圆的对称性 3.1_3.3 练习题 2021—2022学年浙教版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 第3章 圆的对称性 3.1_3.3 练习题 2021—2022学年浙教版九年级数学上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 305.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 22:24:44 | ||
图片预览




文档简介
3.1~3.3 练习题
一、选择题(每小题5分,共30分)
1.已知☉O的半径是6,OP=5,则点P与☉O的位置关系是
( )
A.点P在☉O内
B.点P在☉O上
C.点P在☉O外
D.不能确定
2.下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后能与原图形完全重合的是
( )
图1
3.已知点A,B,C在☉O上,则下列命题为真命题的是
( )
A.若半径OB平分弦AC,则四边形OABC是平行四边形
B.若四边形OABC是平行四边形,则∠ABC=120°
C.若∠ABC=120°,则弦AC平分半径OB
D.若弦AC平分半径OB,则半径OB平分弦AC
4.如图2,AB,BC是☉O的两条弦,AO⊥BC,垂足为D.若☉O的半径为5,BC=8,则AB的长为
( )
图2
A.8
B.10
C.4
D.4
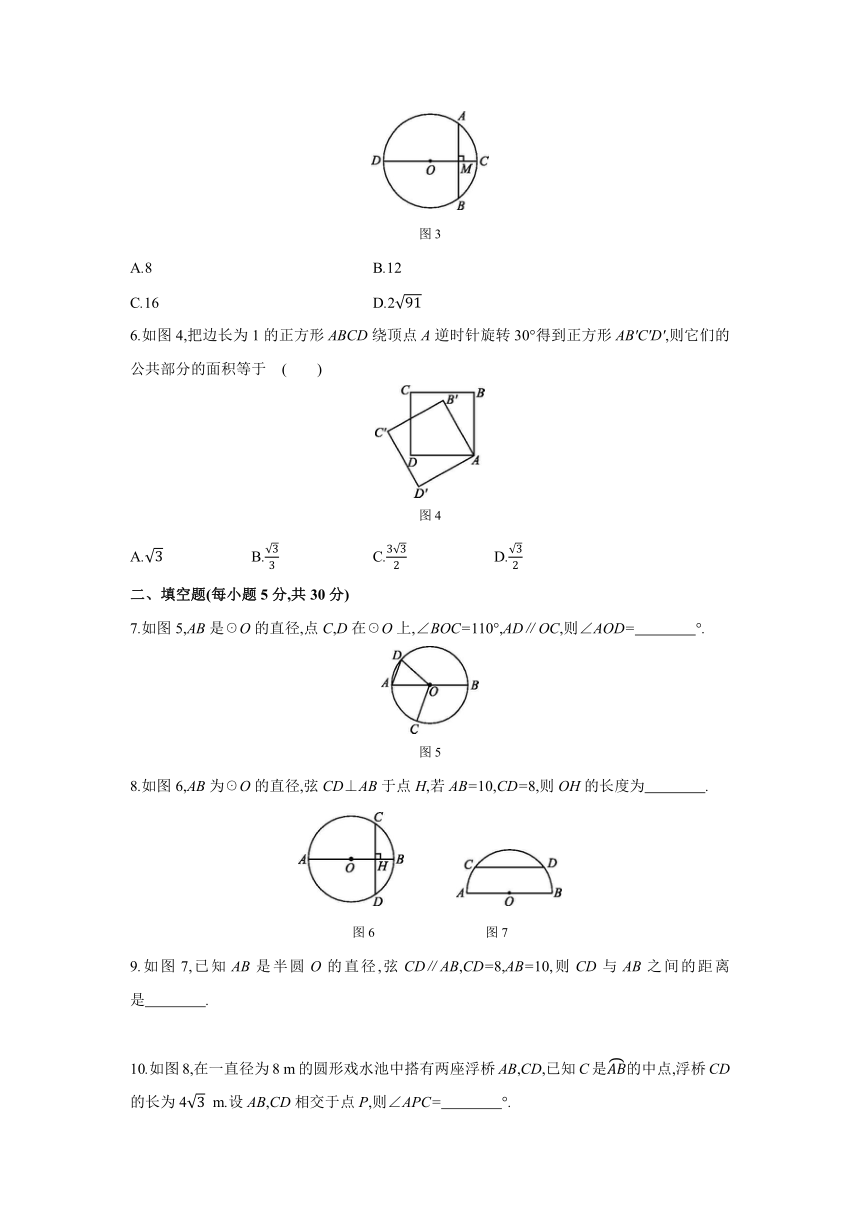
5.如图3,☉O的直径CD=20,AB是☉O的弦,AB⊥CD,垂足为M,OM∶OC=3∶5,则AB的长为
( )
图3
A.8
B.12
C.16
D.2
6.如图4,把边长为1的正方形ABCD绕顶点A逆时针旋转30°得到正方形AB'C'D',则它们的公共部分的面积等于
( )
图4
A.
B.
C.
D.
二、填空题(每小题5分,共30分)
7.如图5,AB是☉O的直径,点C,D在☉O上,∠BOC=110°,AD∥OC,则∠AOD= °.?
图5
8.如图6,AB为☉O的直径,弦CD⊥AB于点H,若AB=10,CD=8,则OH的长度为 .?
图6
图7
9.如图7,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是 .?
10.如图8,在一直径为8
m的圆形戏水池中搭有两座浮桥AB,CD,已知C是的中点,浮桥CD的长为4
m.设AB,CD相交于点P,则∠APC= °.?
图8
11.已知☉O的直径为10
cm,AB,CD是☉O的两条弦,AB∥CD,AB=8
cm,CD=6
cm,则AB与CD之间的距离为 cm.?
12.A,C为半径是3的圆周上两点,B为的中点,以线段BA,BC为邻边作菱形ABCD,若顶点D恰在该圆直径的三等分点上,则该菱形的边长为 .?
三、解答题(共40分)
13.(12分)已知:在△ABC中,AB=AC.
(1)求作:△ABC的外接圆;(要求:尺规作图,保留作图痕迹,不写作法)
(2)若△ABC的外接圆的圆心O到BC边的距离为8,BC=12,求☉O的面积.
图9
14.(12分)如图10,某地有一座圆弧形拱桥,桥下水面宽度AB为7.2
m,拱高CD为2.4
m.
(1)求拱桥所在圆的半径;
(2)现有一艘宽3
m,船舱顶部为长方形并高出水面2
m的货船要经过这里,则此货船能顺利通过该拱桥吗?
图10
15.(16分)如图11,AB,CD是半径为5的☉O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,且点E,F在圆心O的两侧.若P为EF上任意一点,求PA+PC的最小值.
图11
答案
1.A [解析]
∵OP=5<6,
∴点P与☉O的位置关系是点P在☉O内.
故选A.
2.A
3.B [解析]
选项
分析
图示
真假命题
A
如图,若OB平分AC,无法推出四边形OABC是平行四边形
假
B
如图,若四边形OABC是平行四边形,则AB=OC=OA=BC=OB,
∴△OAB和△OBC都是等边三角形,
∴∠ABC=∠ABO+∠OBC=120°
真
C
如图,若∠ABC=120°,无法推出AC平分OB
假
D
如图,若AC平分OB,无法推出OB平分AC
假
4.D [解析]
连结OB,如图.
∵AD⊥BC,AD过点O,BC=8,
∴BD=CD=4,∠BDO=90°.
在Rt△ODB中,由勾股定理得OD===3,
∴AD=AO+OD=5+3=8.
在Rt△ADB中,由勾股定理得AB==4.
故选D.
5.C [解析]
如图,连结OA.
∵☉O的直径CD=20,
∴OA=OC=10.
又∵OM∶OC=3∶5,
∴OM=6.
∵AB⊥CD,∴∠AMO=90°,AM=BM,
∴AM===8,
∴AB=2AM=16.
6.B [解析]
如图,设CD,B'C'相交于点M,连结AM.设DM=x,根据旋转的性质以及正方形的性质可得AB'=AD,∠BAB'=30°,∠B'=∠D=90°.
又∵AM=AM,
∴Rt△AB'M≌Rt△ADM,
∴∠MAD=∠MAB'.
∵∠BAB'=30°,
∴∠MAD=30°,则AM=2x.
在Rt△ADM中,由勾股定理,得x2+1=4x2,∴x=(负值已舍去),
∴S△ADM=×1×=,
∴它们公共部分的面积S四边形ADMB'=2×=.故选B.
7.40 [解析]
∵∠BOC=110°,∠BOC+∠AOC=180°,∴∠AOC=70°.
∵AD∥OC,∴∠A=∠AOC=70°.
又∵OD=OA,∴∠D=∠A=70°,
∴∠AOD=180°-2∠A=40°.
8.3 [解析]
连结OC.
∵AB为☉O的直径,AB=10,∴OC=5.
∵弦CD⊥AB于点H,CD=8,∴CH=4.
在Rt△OCH中,由勾股定理得OH===3.
故答案为3.
9.3 [解析]
过点O作OH⊥CD于点H,连结OC,如图,则CH=DH=CD=4.
∵AB是半圆O的直径,AB=10,∴OC=5.
在Rt△OCH中,OH==3,
∴CD与AB之间的距离是3.故答案为3.
10.60 [解析]
如图,过点O作OM⊥CD于点M,连结OC,交AB于点N.
∵C是的中点,∴OC⊥AB.
∵CD=4,OM⊥CD,∴CM=CD=2,
∴在Rt△OCM中,OM==2.
∵OM=OC,∴∠OCM=30°,
∴∠APC=90°-∠OCM=60°.
11.7或1 [解析]
(1)当圆心O在AB,CD之间时,如图①,
过圆心O作OM⊥AB于点M,延长MO交CD于点N,连结OB,OD.
∵AB∥CD,∴MN⊥CD.
由垂径定理可知MB=4,ND=3,
∴OM==3,ON==4,
∴MN=OM+ON=7;
(2)当圆心O在AB,CD同侧时,如图②,
过圆心O作OM⊥AB于点M,延长OM交CD于点N,则ON⊥CD.
同(1)可得OM=3,ON=4,
∴MN=ON-OM=1.
综上所述,AB与CD之间的距离为7
cm或1
cm.
12.或2 [解析]
分两种情况讨论:如图①所示,若对角线BD=2,连结OA,AC,AC交BD于点E,则AE⊥BD,BE=ED=1,OE=2.根据勾股定理,在Rt△AOE中,AE2=OA2-OE2=9-4=5;在Rt△AED中,AD2=AE2+ED2=6,∴AD=,即菱形的边长为;如图②所示,若对角线BD=4,同理,有OE=OD=1,根据勾股定理,在Rt△AOE中,AE2=OA2-OE2=9-1=8;在Rt△AED中,AD2=AE2+ED2=12,∴AD=2,即菱形的边长为2.综上可知,该菱形的边长为或2.
13.解:(1)如图,☉O即为所画的图形.
(2)如图,连结OB,设线段BC的垂直平分线交BC于点E.
由题意得OE=8,BE=EC=6.
在Rt△BOE中,OB==10,
∴S☉O=πr2=π×102=100π.
14.解:(1)设拱桥所在圆的圆心为O,连结OB,OD,如图,则点C,D,O在同一条直线上,且OC⊥AB,
∴BD=AB=3.6
m.
设OB=OC=r
m,则OD=(r-2.4)m.
在Rt△BOD中,OB2=OD2+BD2,
即r2=(r-2.4)2+3.62,解得r=3.9.
∴拱桥所在圆的半径为3.9
m.
(2)作出拱桥下的矩形MNQP,使NQ=2
m,且点M,N在上,点P,Q在AB上,如图.
设MN交CD于点E,连结ON,则OC⊥MN,DE=NQ=2
m.
∵CD=2.4
m,∴CE=CD-DE=0.4
m,
∴OE=OC-CE=3.9-0.4=3.5(m).
在Rt△OEN中,EN===(m),
∵OC⊥MN,
∴MN=2EN=2×≈3.44(m)>3
m,
∴此货船能顺利通过该拱桥.
15.解:如图,连结AD,过点D作DH⊥AB于点H.
∵MN是☉O的直径,CD⊥MN,
∴点C,D关于MN对称,∴PC=PD,
∴当P为AD与MN的交点时,PA+PC的值最小.
连结AO,CO.
∵AB⊥MN于点E,∴AE=AB=4.
又∵AO=5,∴EO==3.
同理,CF=DF=3,可求得OF=4,∴EF=7.
∵DH⊥AB,AB⊥MN,CD⊥MN,
∴∠FEH=∠EFD=∠DHE=90°,
∴四边形EHDF为矩形,
∴DH=EF=7,EH=DF=3,
∴AH=AE+EH=4+3=7.
在Rt△AHD中,根据勾股定理,得
AD==7,
∴PA+PC的最小值为7.
一、选择题(每小题5分,共30分)
1.已知☉O的半径是6,OP=5,则点P与☉O的位置关系是
( )
A.点P在☉O内
B.点P在☉O上
C.点P在☉O外
D.不能确定
2.下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后能与原图形完全重合的是
( )
图1
3.已知点A,B,C在☉O上,则下列命题为真命题的是
( )
A.若半径OB平分弦AC,则四边形OABC是平行四边形
B.若四边形OABC是平行四边形,则∠ABC=120°
C.若∠ABC=120°,则弦AC平分半径OB
D.若弦AC平分半径OB,则半径OB平分弦AC
4.如图2,AB,BC是☉O的两条弦,AO⊥BC,垂足为D.若☉O的半径为5,BC=8,则AB的长为
( )
图2
A.8
B.10
C.4
D.4
5.如图3,☉O的直径CD=20,AB是☉O的弦,AB⊥CD,垂足为M,OM∶OC=3∶5,则AB的长为
( )
图3
A.8
B.12
C.16
D.2
6.如图4,把边长为1的正方形ABCD绕顶点A逆时针旋转30°得到正方形AB'C'D',则它们的公共部分的面积等于
( )
图4
A.
B.
C.
D.
二、填空题(每小题5分,共30分)
7.如图5,AB是☉O的直径,点C,D在☉O上,∠BOC=110°,AD∥OC,则∠AOD= °.?
图5
8.如图6,AB为☉O的直径,弦CD⊥AB于点H,若AB=10,CD=8,则OH的长度为 .?
图6
图7
9.如图7,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是 .?
10.如图8,在一直径为8
m的圆形戏水池中搭有两座浮桥AB,CD,已知C是的中点,浮桥CD的长为4
m.设AB,CD相交于点P,则∠APC= °.?
图8
11.已知☉O的直径为10
cm,AB,CD是☉O的两条弦,AB∥CD,AB=8
cm,CD=6
cm,则AB与CD之间的距离为 cm.?
12.A,C为半径是3的圆周上两点,B为的中点,以线段BA,BC为邻边作菱形ABCD,若顶点D恰在该圆直径的三等分点上,则该菱形的边长为 .?
三、解答题(共40分)
13.(12分)已知:在△ABC中,AB=AC.
(1)求作:△ABC的外接圆;(要求:尺规作图,保留作图痕迹,不写作法)
(2)若△ABC的外接圆的圆心O到BC边的距离为8,BC=12,求☉O的面积.
图9
14.(12分)如图10,某地有一座圆弧形拱桥,桥下水面宽度AB为7.2
m,拱高CD为2.4
m.
(1)求拱桥所在圆的半径;
(2)现有一艘宽3
m,船舱顶部为长方形并高出水面2
m的货船要经过这里,则此货船能顺利通过该拱桥吗?
图10
15.(16分)如图11,AB,CD是半径为5的☉O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,且点E,F在圆心O的两侧.若P为EF上任意一点,求PA+PC的最小值.
图11
答案
1.A [解析]
∵OP=5<6,
∴点P与☉O的位置关系是点P在☉O内.
故选A.
2.A
3.B [解析]
选项
分析
图示
真假命题
A
如图,若OB平分AC,无法推出四边形OABC是平行四边形
假
B
如图,若四边形OABC是平行四边形,则AB=OC=OA=BC=OB,
∴△OAB和△OBC都是等边三角形,
∴∠ABC=∠ABO+∠OBC=120°
真
C
如图,若∠ABC=120°,无法推出AC平分OB
假
D
如图,若AC平分OB,无法推出OB平分AC
假
4.D [解析]
连结OB,如图.
∵AD⊥BC,AD过点O,BC=8,
∴BD=CD=4,∠BDO=90°.
在Rt△ODB中,由勾股定理得OD===3,
∴AD=AO+OD=5+3=8.
在Rt△ADB中,由勾股定理得AB==4.
故选D.
5.C [解析]
如图,连结OA.
∵☉O的直径CD=20,
∴OA=OC=10.
又∵OM∶OC=3∶5,
∴OM=6.
∵AB⊥CD,∴∠AMO=90°,AM=BM,
∴AM===8,
∴AB=2AM=16.
6.B [解析]
如图,设CD,B'C'相交于点M,连结AM.设DM=x,根据旋转的性质以及正方形的性质可得AB'=AD,∠BAB'=30°,∠B'=∠D=90°.
又∵AM=AM,
∴Rt△AB'M≌Rt△ADM,
∴∠MAD=∠MAB'.
∵∠BAB'=30°,
∴∠MAD=30°,则AM=2x.
在Rt△ADM中,由勾股定理,得x2+1=4x2,∴x=(负值已舍去),
∴S△ADM=×1×=,
∴它们公共部分的面积S四边形ADMB'=2×=.故选B.
7.40 [解析]
∵∠BOC=110°,∠BOC+∠AOC=180°,∴∠AOC=70°.
∵AD∥OC,∴∠A=∠AOC=70°.
又∵OD=OA,∴∠D=∠A=70°,
∴∠AOD=180°-2∠A=40°.
8.3 [解析]
连结OC.
∵AB为☉O的直径,AB=10,∴OC=5.
∵弦CD⊥AB于点H,CD=8,∴CH=4.
在Rt△OCH中,由勾股定理得OH===3.
故答案为3.
9.3 [解析]
过点O作OH⊥CD于点H,连结OC,如图,则CH=DH=CD=4.
∵AB是半圆O的直径,AB=10,∴OC=5.
在Rt△OCH中,OH==3,
∴CD与AB之间的距离是3.故答案为3.
10.60 [解析]
如图,过点O作OM⊥CD于点M,连结OC,交AB于点N.
∵C是的中点,∴OC⊥AB.
∵CD=4,OM⊥CD,∴CM=CD=2,
∴在Rt△OCM中,OM==2.
∵OM=OC,∴∠OCM=30°,
∴∠APC=90°-∠OCM=60°.
11.7或1 [解析]
(1)当圆心O在AB,CD之间时,如图①,
过圆心O作OM⊥AB于点M,延长MO交CD于点N,连结OB,OD.
∵AB∥CD,∴MN⊥CD.
由垂径定理可知MB=4,ND=3,
∴OM==3,ON==4,
∴MN=OM+ON=7;
(2)当圆心O在AB,CD同侧时,如图②,
过圆心O作OM⊥AB于点M,延长OM交CD于点N,则ON⊥CD.
同(1)可得OM=3,ON=4,
∴MN=ON-OM=1.
综上所述,AB与CD之间的距离为7
cm或1
cm.
12.或2 [解析]
分两种情况讨论:如图①所示,若对角线BD=2,连结OA,AC,AC交BD于点E,则AE⊥BD,BE=ED=1,OE=2.根据勾股定理,在Rt△AOE中,AE2=OA2-OE2=9-4=5;在Rt△AED中,AD2=AE2+ED2=6,∴AD=,即菱形的边长为;如图②所示,若对角线BD=4,同理,有OE=OD=1,根据勾股定理,在Rt△AOE中,AE2=OA2-OE2=9-1=8;在Rt△AED中,AD2=AE2+ED2=12,∴AD=2,即菱形的边长为2.综上可知,该菱形的边长为或2.
13.解:(1)如图,☉O即为所画的图形.
(2)如图,连结OB,设线段BC的垂直平分线交BC于点E.
由题意得OE=8,BE=EC=6.
在Rt△BOE中,OB==10,
∴S☉O=πr2=π×102=100π.
14.解:(1)设拱桥所在圆的圆心为O,连结OB,OD,如图,则点C,D,O在同一条直线上,且OC⊥AB,
∴BD=AB=3.6
m.
设OB=OC=r
m,则OD=(r-2.4)m.
在Rt△BOD中,OB2=OD2+BD2,
即r2=(r-2.4)2+3.62,解得r=3.9.
∴拱桥所在圆的半径为3.9
m.
(2)作出拱桥下的矩形MNQP,使NQ=2
m,且点M,N在上,点P,Q在AB上,如图.
设MN交CD于点E,连结ON,则OC⊥MN,DE=NQ=2
m.
∵CD=2.4
m,∴CE=CD-DE=0.4
m,
∴OE=OC-CE=3.9-0.4=3.5(m).
在Rt△OEN中,EN===(m),
∵OC⊥MN,
∴MN=2EN=2×≈3.44(m)>3
m,
∴此货船能顺利通过该拱桥.
15.解:如图,连结AD,过点D作DH⊥AB于点H.
∵MN是☉O的直径,CD⊥MN,
∴点C,D关于MN对称,∴PC=PD,
∴当P为AD与MN的交点时,PA+PC的值最小.
连结AO,CO.
∵AB⊥MN于点E,∴AE=AB=4.
又∵AO=5,∴EO==3.
同理,CF=DF=3,可求得OF=4,∴EF=7.
∵DH⊥AB,AB⊥MN,CD⊥MN,
∴∠FEH=∠EFD=∠DHE=90°,
∴四边形EHDF为矩形,
∴DH=EF=7,EH=DF=3,
∴AH=AE+EH=4+3=7.
在Rt△AHD中,根据勾股定理,得
AD==7,
∴PA+PC的最小值为7.
同课章节目录
