1.5三角形全等的判定 能力提升训练(Word版 附答案) 2021-2022学年浙教版八年级数学上册
文档属性
| 名称 | 1.5三角形全等的判定 能力提升训练(Word版 附答案) 2021-2022学年浙教版八年级数学上册 |
|
|
| 格式 | doc | ||
| 文件大小 | 195.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 00:00:00 | ||
图片预览


文档简介
2021-2022学年浙教版八年级数学上册《1.5三角形全等的判定》能力提升训练(附答案)
一、选择题
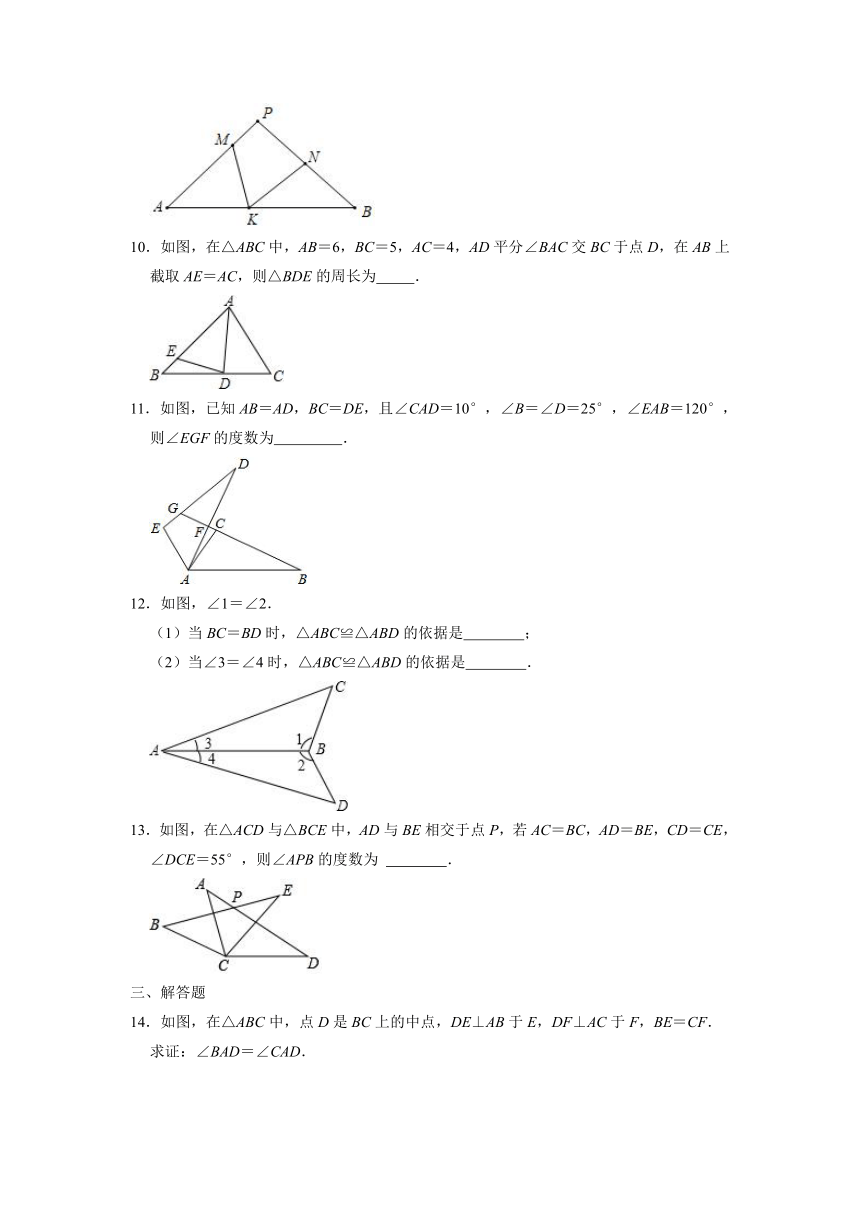
1.如图,点B在线段AC上,AD∥BE,AD=BC,再补充下列一个条件,不能证明△ADB≌△BCE的是( )
A.∠ABD=∠E
B.∠D=∠C
C.AB=BE
D.BD=EC
2.如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择了一点C,测得∠ABC=75°,∠ACB=35°,然后在M处立了标杆,使∠CBM=75°,∠MCB=35°,得到△MBC≌△ABC,所以测得MB的长就是A,B两点间的距离,这里判定△MBC≌△ABC的理由是( )
A.SAS
B.AAA
C.SSS
D.ASA
3.如图,下列条件中,不能证明△ABD≌△ACD的是( )
A.BD=DC,AB=AC
B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD
D.∠B=∠C,BD=DC
4.如图,D是AB上一点,DF交AC于点E,FC∥AB,则下列结论错误的是( )
A.若AE=CE,则DE=FE
B.若DE=FE,则AE=CE
C.若BC=CF,则AD=CF
D.若AD=CF,则DE=FE
5.如图,AB=CD,∠ABC=∠DCB,AC与BD交于点E,在图中全等三角形有( )
A.2对
B.3对
C.4对
D.5对
6.如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块完全一样形状的玻璃.那么最省事的办法是带( )
A.带①去
B.带②去
C.带③去
D.带①②去
7.工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M、N重合,过角尺顶点C作射线OC,由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS
B.SAS
C.ASA
D.AAS
8.如图,已知AD=AE,BE=CD,∠1=∠2=100°,∠BAE=60°,则∠CAE的度数为( )
A.20°
B.30°
C.40°
D.50°
二、填空题
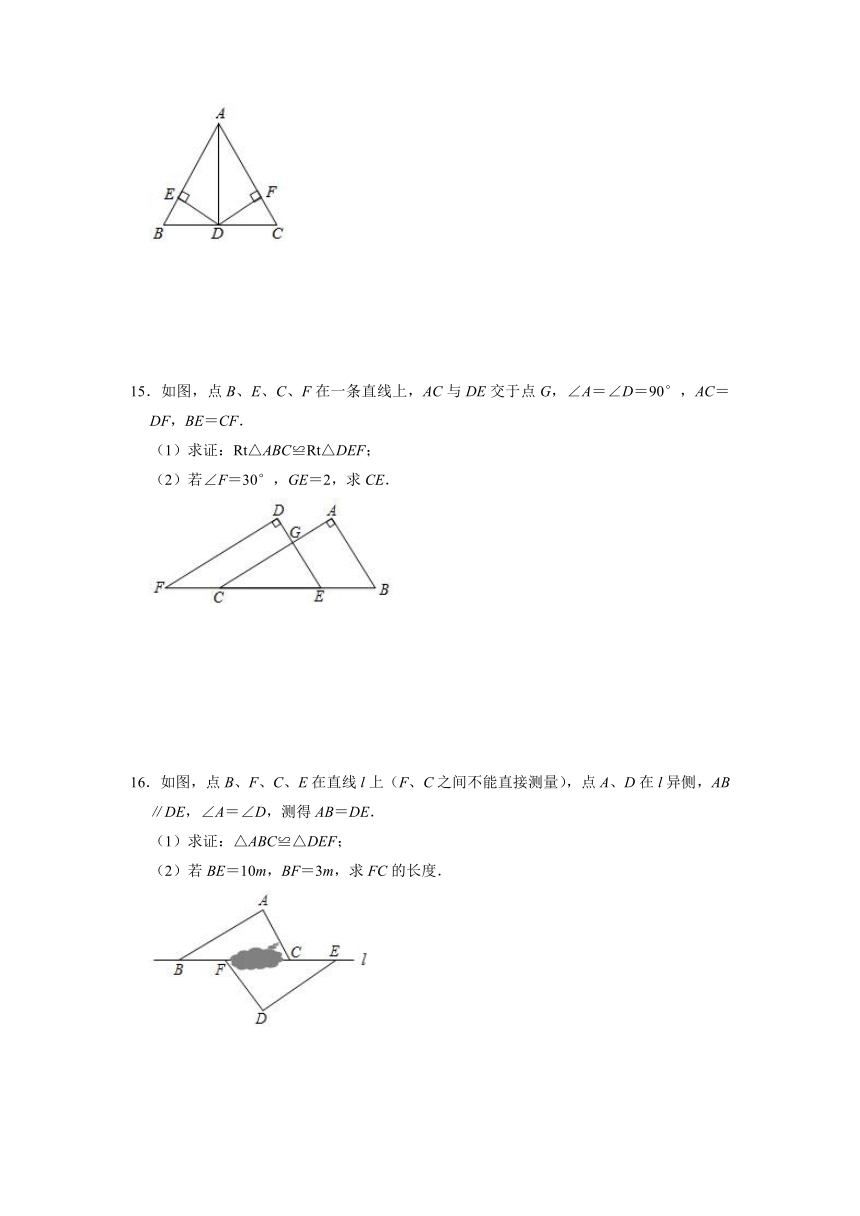
9.如图,在△PAB中,PA=PB,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为
.
10.如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D,在AB上截取AE=AC,则△BDE的周长为
.
11.如图,已知AB=AD,BC=DE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,则∠EGF的度数为
.
12.如图,∠1=∠2.
(1)当BC=BD时,△ABC≌△ABD的依据是
;
(2)当∠3=∠4时,△ABC≌△ABD的依据是
.
13.如图,在△ACD与△BCE中,AD与BE相交于点P,若AC=BC,AD=BE,CD=CE,∠DCE=55°,则∠APB的度数为
.
三、解答题
14.如图,在△ABC中,点D是BC上的中点,DE⊥AB于E,DF⊥AC于F,BE=CF.
求证:∠BAD=∠CAD.
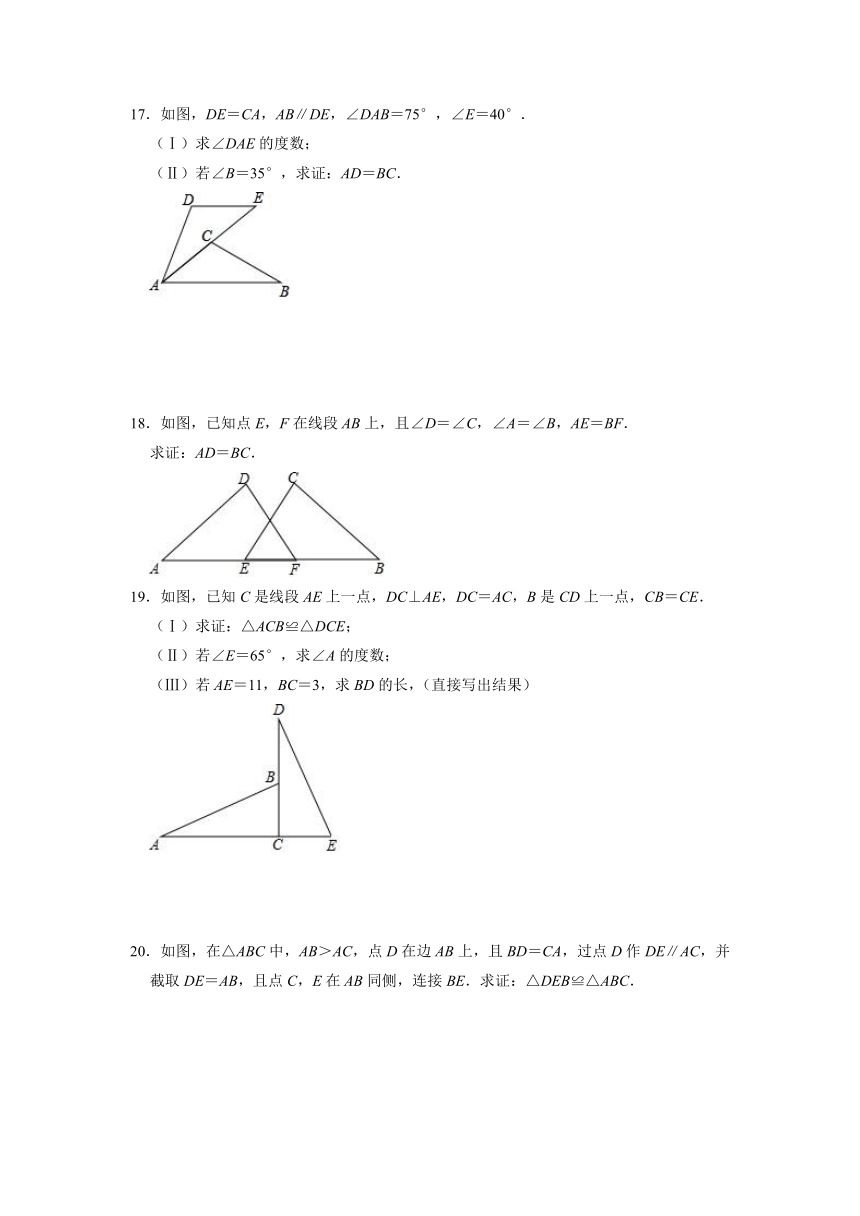
15.如图,点B、E、C、F在一条直线上,AC与DE交于点G,∠A=∠D=90°,AC=DF,BE=CF.
(1)求证:Rt△ABC≌Rt△DEF;
(2)若∠F=30°,GE=2,求CE.
16.如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,AB∥DE,∠A=∠D,测得AB=DE.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
17.如图,DE=CA,AB∥DE,∠DAB=75°,∠E=40°.
(Ⅰ)求∠DAE的度数;
(Ⅱ)若∠B=35°,求证:AD=BC.
18.如图,已知点E,F在线段AB上,且∠D=∠C,∠A=∠B,AE=BF.
求证:AD=BC.
19.如图,已知C是线段AE上一点,DC⊥AE,DC=AC,B是CD上一点,CB=CE.
(Ⅰ)求证:△ACB≌△DCE;
(Ⅱ)若∠E=65°,求∠A的度数;
(Ⅲ)若AE=11,BC=3,求BD的长,(直接写出结果)
20.如图,在△ABC中,AB>AC,点D在边AB上,且BD=CA,过点D作DE∥AC,并截取DE=AB,且点C,E在AB同侧,连接BE.求证:△DEB≌△ABC.
21.如图,在△ABC和△ADE中,AB=AD,AC=AE,∠1=∠2,AD、BC相交于点F.
(1)求证:∠B=∠D;
(2)若AB∥DE,AE=3,DE=4,求△ACF的周长.
参考答案
1.解:∵AD∥BE,
∴∠A=∠EBC,
A、根据AAS,推出△ADB≌△BCE,本选项不符合题意.
B、根据ASA,推出△ADB≌△BCE,本选项不符合题意.
C、根据SAS,推出△ADB≌△BCE,本选项不符合题意.
D、SSA,不能判断三角形全等,本选项符合题意,
故选:D.
2.解:在△ABC和△MBC中,
∴△MBC≌△ABC(ASA),
故选:D.
3.解:A、依据SSS可知△ABD≌△ACD,故A不符合要求;
B、依据SAS可知△ABD≌△ACD,故B不符合要求;
C、依据AAS可知△ABD≌△ACD,故C不符合要求;
D、依据SSA可知△ABD≌△ACD,故D符合要求.
故选:D.
4.解:
∵AB∥FC,
∴∠A=∠ACF,∠ADE=∠F,
当AE=CE时,利用AAS则可证得△ADE≌△CFE,则有DE=EF,故A选项说法是正确的,不符合题意,
当DE=FE时,同理可证得△ADE≌△CFE,则有AE=CE,故B选项说法是正确的,不符合题意,
当BC=CF时,无法证明△ADE≌△CFE,即无法得出AD=CF,故C说法是错误的,符合题意,
当AD=CF时,利用ASA则可证得△ADE≌△CFE,则有DE=FE,故D选项是正确的,不符合题意,
故选:C.
5.解:①△ABC≌△DCB;
∵AB=CD,∠ABC=∠DCB,
∵BC=CB,
∴△ABC≌△DCB;
②△ABE≌△DCE,
∵△ABC≌△DCB,
∴∠BAC=∠CDB,
∵AB=CD,∠AEB=∠DEC,
∴△ABE≌△CDE;
③△ABD≌△DCA,
∵∠BAC=∠CDB,∠AEB=∠DEC,
∴∠ABD=∠DCA,
∵AB=CD,BD=AC,
∴△ABD≌△DCA;
故选:B.
6.解:第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;
第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.
故选:C.
7.解:∵在△ONC和△OMC中,
∴△MOC≌△NOC(SSS),
∴∠BOC=∠AOC,
故选:A.
8.解:∵∠1=∠2=100°,
∴∠ADE=∠AED=80°,
∴∠DAE=180°﹣∠ADE﹣∠AED=20°,
∵AD=AE,∠ADE=∠AED,BE=CD,
∴△AEB≌△ADC(SAS)
∴∠BAE=∠CAD=60°,
∴∠CAE=∠CAD﹣∠DAE=40°,
故选:C.
9.解:∵PA=PB,
∴∠A=∠B,
在△AMK和△BKN中,
,
∴△AMK≌△BKN(SAS),
∴∠AMK=∠BKN,
∵∠A+∠AMK=∠MKN+∠BKN,
∴∠A=∠MKN=40°,
∴∠P=180°﹣∠A﹣∠B=180°﹣40°﹣40°=100°,
故答案为100°.
10.解:∵AD是∠BAC的平分线,
∴∠EAD=∠CAD
在△ADE和△ADC中,
,
∴△ADE≌△ADC(SAS),
∴ED=CD,
∴BC=BD+CD=DE+BD=5,
∴△BDE的周长=BE+BD+ED=(6﹣4)+5=7.
故答案为:7
11.解:∵AB=AD,BC=DE,∠B=∠D=25°,
∴△ABC≌△ADE(SAS)
∴∠DAE=∠CAB,
∵∠EAB=120°,∠CAD=10°,
∴∠EAD=∠CAB=55°,
∴∠DAB=65°,
∵∠GFD=∠AFB,∠B=∠D=25°,
∴∠DGB=∠DAB=65°,
∴∠EGF=115°
故答案为:115°.
12.解:(1)∵∠1=∠2,AB=AB,BC=BD
∴△ABC≌△ABD(SAS);
(2)∵∠1=∠2,AB=AB,∠3=∠4
∴△ABC≌△ABD(ASA).
故答案为SAS、ASA.
13.解:在△ACD和△BCE中,
,
∴△ACD≌△BCE(SSS),
∴∠D=∠E,
∵∠DPE+∠1+∠E=∠DCE+∠2+∠D,
而∠1=∠2,
∴∠DPE=∠DCE=55°,
∴∠APB=∠DPE=55°.
故答案为55°.
14.证明:∵D是BC的中点,
∴BD=CD,
∵DE⊥AB,DF⊥AC,
在Rt△BED和Rt△CFD中,
,
∴Rt△BED≌Rt△CFD(HL),
∴DE=DF,
∴点D在∠BAC的平分线上,
∴AD平分∠BAC,
∴∠BAD=∠CAD.
15.(1)∵BE=CF
∴BE+CE=CF+CE
即BC=EF
在Rt△ABC和Rt△DEF中
∴Rt△ABC≌Rt△DEF(HL)
(2)∵Rt△ABC≌Rt△DEF
∴∠ACE=∠F
∵∠F=30°
∴∠ACE=30°
∴AC∥DF
∴∠CGE=∠D
∵∠D=90°
∴∠CGE=90°
∵在Rt△CGE中,∠ACB=30°,GE=2
∴CE=2GE=4
16.(1)证明:∵AB∥DE,
∴∠ABC=∠DEF,
在△ABC与△DEF中
,
∴△ABC≌△DEF;
(2)∵△ABC≌△DEF,
∴BC=EF,
∴BF+FC=EC+FC,
∴BF=EC,
∵BE=10m,BF=3m,
∴FC=10﹣3﹣3=4m.
17.解:(Ⅰ)∵AB∥DE,
∴∠E=∠CAB=40°,
∵∠DAB=75°,
∴∠DAE=35°;
(Ⅱ)∵∠B=35°,
∴∠B=∠DAE,
在△ADE和△BCA中,
,
∴△ADE≌△BCA(AAS),
∴AD=BC.
18.证明:∵AE=BF,
∴AE+EF=BF+EF,
∴AF=BE,
在△ADF与△BCE中,,
∴△ADF≌△BCE(AAS),
∴AD=BC.
19.证明:(Ⅰ)∵DC=AC,∠ACB=∠DCE=90°,BC=CE
∴△ACB≌△DCE(SAS)
(Ⅱ)∵△ACB≌△DCE,
∴∠E=∠ABC=65°
∴∠A=90°﹣∠ABC=25°
(Ⅲ)∵△ACB≌△DCE
∴AC=DC,BC=CE=3,
∴AC=AE﹣CE=11﹣3=8=CD
∴BD=CD﹣BC=8﹣3=5
20.证明:∵DE∥AC,
∴∠EDB=∠A.
在△DEB与△ABC中,
,
∴△DEB≌△ABC(SAS).
21.解:(1)证明:∵∠1=∠2,
∴∠1+∠CAD=∠2+∠CAD,
∴∠CAB=∠EAD,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(SAS),
∴∠B=∠D;
(2)∵AB∥DE,
∴∠D=∠1,
∵∠B=∠D,
∴∠1=∠B,
∴FA=FB,
∴FA+FC=FB+FC=BC,
∵△ABC≌△ADE,
∴AC=AE=3,BC=DE=4,
∴△ACF的周长为:AC+AF+CF=AC+BC=7
一、选择题
1.如图,点B在线段AC上,AD∥BE,AD=BC,再补充下列一个条件,不能证明△ADB≌△BCE的是( )
A.∠ABD=∠E
B.∠D=∠C
C.AB=BE
D.BD=EC
2.如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择了一点C,测得∠ABC=75°,∠ACB=35°,然后在M处立了标杆,使∠CBM=75°,∠MCB=35°,得到△MBC≌△ABC,所以测得MB的长就是A,B两点间的距离,这里判定△MBC≌△ABC的理由是( )
A.SAS
B.AAA
C.SSS
D.ASA
3.如图,下列条件中,不能证明△ABD≌△ACD的是( )
A.BD=DC,AB=AC
B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD
D.∠B=∠C,BD=DC
4.如图,D是AB上一点,DF交AC于点E,FC∥AB,则下列结论错误的是( )
A.若AE=CE,则DE=FE
B.若DE=FE,则AE=CE
C.若BC=CF,则AD=CF
D.若AD=CF,则DE=FE
5.如图,AB=CD,∠ABC=∠DCB,AC与BD交于点E,在图中全等三角形有( )
A.2对
B.3对
C.4对
D.5对
6.如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块完全一样形状的玻璃.那么最省事的办法是带( )
A.带①去
B.带②去
C.带③去
D.带①②去
7.工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M、N重合,过角尺顶点C作射线OC,由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS
B.SAS
C.ASA
D.AAS
8.如图,已知AD=AE,BE=CD,∠1=∠2=100°,∠BAE=60°,则∠CAE的度数为( )
A.20°
B.30°
C.40°
D.50°
二、填空题
9.如图,在△PAB中,PA=PB,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为
.
10.如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D,在AB上截取AE=AC,则△BDE的周长为
.
11.如图,已知AB=AD,BC=DE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,则∠EGF的度数为
.
12.如图,∠1=∠2.
(1)当BC=BD时,△ABC≌△ABD的依据是
;
(2)当∠3=∠4时,△ABC≌△ABD的依据是
.
13.如图,在△ACD与△BCE中,AD与BE相交于点P,若AC=BC,AD=BE,CD=CE,∠DCE=55°,则∠APB的度数为
.
三、解答题
14.如图,在△ABC中,点D是BC上的中点,DE⊥AB于E,DF⊥AC于F,BE=CF.
求证:∠BAD=∠CAD.
15.如图,点B、E、C、F在一条直线上,AC与DE交于点G,∠A=∠D=90°,AC=DF,BE=CF.
(1)求证:Rt△ABC≌Rt△DEF;
(2)若∠F=30°,GE=2,求CE.
16.如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,AB∥DE,∠A=∠D,测得AB=DE.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
17.如图,DE=CA,AB∥DE,∠DAB=75°,∠E=40°.
(Ⅰ)求∠DAE的度数;
(Ⅱ)若∠B=35°,求证:AD=BC.
18.如图,已知点E,F在线段AB上,且∠D=∠C,∠A=∠B,AE=BF.
求证:AD=BC.
19.如图,已知C是线段AE上一点,DC⊥AE,DC=AC,B是CD上一点,CB=CE.
(Ⅰ)求证:△ACB≌△DCE;
(Ⅱ)若∠E=65°,求∠A的度数;
(Ⅲ)若AE=11,BC=3,求BD的长,(直接写出结果)
20.如图,在△ABC中,AB>AC,点D在边AB上,且BD=CA,过点D作DE∥AC,并截取DE=AB,且点C,E在AB同侧,连接BE.求证:△DEB≌△ABC.
21.如图,在△ABC和△ADE中,AB=AD,AC=AE,∠1=∠2,AD、BC相交于点F.
(1)求证:∠B=∠D;
(2)若AB∥DE,AE=3,DE=4,求△ACF的周长.
参考答案
1.解:∵AD∥BE,
∴∠A=∠EBC,
A、根据AAS,推出△ADB≌△BCE,本选项不符合题意.
B、根据ASA,推出△ADB≌△BCE,本选项不符合题意.
C、根据SAS,推出△ADB≌△BCE,本选项不符合题意.
D、SSA,不能判断三角形全等,本选项符合题意,
故选:D.
2.解:在△ABC和△MBC中,
∴△MBC≌△ABC(ASA),
故选:D.
3.解:A、依据SSS可知△ABD≌△ACD,故A不符合要求;
B、依据SAS可知△ABD≌△ACD,故B不符合要求;
C、依据AAS可知△ABD≌△ACD,故C不符合要求;
D、依据SSA可知△ABD≌△ACD,故D符合要求.
故选:D.
4.解:
∵AB∥FC,
∴∠A=∠ACF,∠ADE=∠F,
当AE=CE时,利用AAS则可证得△ADE≌△CFE,则有DE=EF,故A选项说法是正确的,不符合题意,
当DE=FE时,同理可证得△ADE≌△CFE,则有AE=CE,故B选项说法是正确的,不符合题意,
当BC=CF时,无法证明△ADE≌△CFE,即无法得出AD=CF,故C说法是错误的,符合题意,
当AD=CF时,利用ASA则可证得△ADE≌△CFE,则有DE=FE,故D选项是正确的,不符合题意,
故选:C.
5.解:①△ABC≌△DCB;
∵AB=CD,∠ABC=∠DCB,
∵BC=CB,
∴△ABC≌△DCB;
②△ABE≌△DCE,
∵△ABC≌△DCB,
∴∠BAC=∠CDB,
∵AB=CD,∠AEB=∠DEC,
∴△ABE≌△CDE;
③△ABD≌△DCA,
∵∠BAC=∠CDB,∠AEB=∠DEC,
∴∠ABD=∠DCA,
∵AB=CD,BD=AC,
∴△ABD≌△DCA;
故选:B.
6.解:第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;
第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.
故选:C.
7.解:∵在△ONC和△OMC中,
∴△MOC≌△NOC(SSS),
∴∠BOC=∠AOC,
故选:A.
8.解:∵∠1=∠2=100°,
∴∠ADE=∠AED=80°,
∴∠DAE=180°﹣∠ADE﹣∠AED=20°,
∵AD=AE,∠ADE=∠AED,BE=CD,
∴△AEB≌△ADC(SAS)
∴∠BAE=∠CAD=60°,
∴∠CAE=∠CAD﹣∠DAE=40°,
故选:C.
9.解:∵PA=PB,
∴∠A=∠B,
在△AMK和△BKN中,
,
∴△AMK≌△BKN(SAS),
∴∠AMK=∠BKN,
∵∠A+∠AMK=∠MKN+∠BKN,
∴∠A=∠MKN=40°,
∴∠P=180°﹣∠A﹣∠B=180°﹣40°﹣40°=100°,
故答案为100°.
10.解:∵AD是∠BAC的平分线,
∴∠EAD=∠CAD
在△ADE和△ADC中,
,
∴△ADE≌△ADC(SAS),
∴ED=CD,
∴BC=BD+CD=DE+BD=5,
∴△BDE的周长=BE+BD+ED=(6﹣4)+5=7.
故答案为:7
11.解:∵AB=AD,BC=DE,∠B=∠D=25°,
∴△ABC≌△ADE(SAS)
∴∠DAE=∠CAB,
∵∠EAB=120°,∠CAD=10°,
∴∠EAD=∠CAB=55°,
∴∠DAB=65°,
∵∠GFD=∠AFB,∠B=∠D=25°,
∴∠DGB=∠DAB=65°,
∴∠EGF=115°
故答案为:115°.
12.解:(1)∵∠1=∠2,AB=AB,BC=BD
∴△ABC≌△ABD(SAS);
(2)∵∠1=∠2,AB=AB,∠3=∠4
∴△ABC≌△ABD(ASA).
故答案为SAS、ASA.
13.解:在△ACD和△BCE中,
,
∴△ACD≌△BCE(SSS),
∴∠D=∠E,
∵∠DPE+∠1+∠E=∠DCE+∠2+∠D,
而∠1=∠2,
∴∠DPE=∠DCE=55°,
∴∠APB=∠DPE=55°.
故答案为55°.
14.证明:∵D是BC的中点,
∴BD=CD,
∵DE⊥AB,DF⊥AC,
在Rt△BED和Rt△CFD中,
,
∴Rt△BED≌Rt△CFD(HL),
∴DE=DF,
∴点D在∠BAC的平分线上,
∴AD平分∠BAC,
∴∠BAD=∠CAD.
15.(1)∵BE=CF
∴BE+CE=CF+CE
即BC=EF
在Rt△ABC和Rt△DEF中
∴Rt△ABC≌Rt△DEF(HL)
(2)∵Rt△ABC≌Rt△DEF
∴∠ACE=∠F
∵∠F=30°
∴∠ACE=30°
∴AC∥DF
∴∠CGE=∠D
∵∠D=90°
∴∠CGE=90°
∵在Rt△CGE中,∠ACB=30°,GE=2
∴CE=2GE=4
16.(1)证明:∵AB∥DE,
∴∠ABC=∠DEF,
在△ABC与△DEF中
,
∴△ABC≌△DEF;
(2)∵△ABC≌△DEF,
∴BC=EF,
∴BF+FC=EC+FC,
∴BF=EC,
∵BE=10m,BF=3m,
∴FC=10﹣3﹣3=4m.
17.解:(Ⅰ)∵AB∥DE,
∴∠E=∠CAB=40°,
∵∠DAB=75°,
∴∠DAE=35°;
(Ⅱ)∵∠B=35°,
∴∠B=∠DAE,
在△ADE和△BCA中,
,
∴△ADE≌△BCA(AAS),
∴AD=BC.
18.证明:∵AE=BF,
∴AE+EF=BF+EF,
∴AF=BE,
在△ADF与△BCE中,,
∴△ADF≌△BCE(AAS),
∴AD=BC.
19.证明:(Ⅰ)∵DC=AC,∠ACB=∠DCE=90°,BC=CE
∴△ACB≌△DCE(SAS)
(Ⅱ)∵△ACB≌△DCE,
∴∠E=∠ABC=65°
∴∠A=90°﹣∠ABC=25°
(Ⅲ)∵△ACB≌△DCE
∴AC=DC,BC=CE=3,
∴AC=AE﹣CE=11﹣3=8=CD
∴BD=CD﹣BC=8﹣3=5
20.证明:∵DE∥AC,
∴∠EDB=∠A.
在△DEB与△ABC中,
,
∴△DEB≌△ABC(SAS).
21.解:(1)证明:∵∠1=∠2,
∴∠1+∠CAD=∠2+∠CAD,
∴∠CAB=∠EAD,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(SAS),
∴∠B=∠D;
(2)∵AB∥DE,
∴∠D=∠1,
∵∠B=∠D,
∴∠1=∠B,
∴FA=FB,
∴FA+FC=FB+FC=BC,
∵△ABC≌△ADE,
∴AC=AE=3,BC=DE=4,
∴△ACF的周长为:AC+AF+CF=AC+BC=7
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
