《1.4二次函数的应用》同步提升训练2021-2022学年浙教版九年级数学上册(Word版含答案)
文档属性
| 名称 | 《1.4二次函数的应用》同步提升训练2021-2022学年浙教版九年级数学上册(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 153.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 22:42:38 | ||
图片预览



文档简介
2021-2022学年浙教版九年级数学上册《1.4二次函数的应用》同步提升训练(附答案)
一、选择题
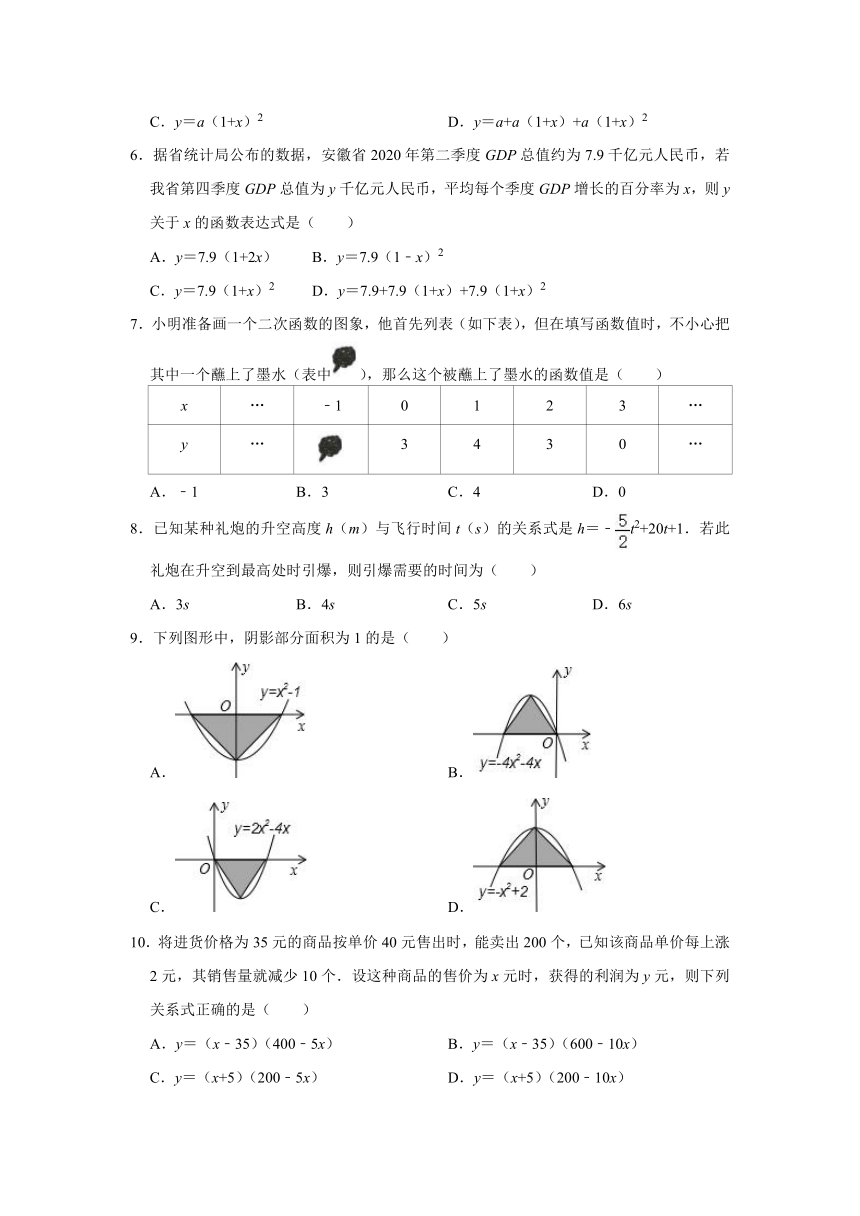
1.已知二次函数y=kx2﹣6x﹣9的图象与x轴有两个不同的交点,则k的取值范围为( )
A.k>﹣1
B.k>﹣1且k≠0
C.k≥﹣1
D.k≥﹣1且k≠0
2.二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表,则方程ax2+bx+c=0的一个解的范围是( )
x
6.17
6.18
6.19
y
﹣0.03
﹣0.01
0.02
A.﹣0.03<x<﹣0.01
B.﹣0.01<x<0.02
C.6.18<x<6.19
D.6.17<x<6.18
3.如图,直线y1=﹣x+k与抛物线y2=ax2(a≠0)交于点A(﹣2,4)和点B.若y1<y2,则x的取值范围是( )
A.x<﹣2
B.﹣2<x<1
C.x<﹣2或x>1
D.x<﹣2或x>
4.如图,直线y1=kx+b与抛物线y2=ax2+bx+c交于A(﹣1,m)、B(4,n)两点,若y1<y2,则x的取值范围( )
A.x<﹣1
B.x>4
C.﹣1<x<4
D.x<﹣1或x>4
5.某工厂2019年产品的产量为a吨,该产品产量的年平均增长率为x(x>0),设2021年该产品的产量为y吨,则y关于x的函数关系式为( )
A.y=a(1﹣x)2
B.y=
C.y=a(1+x)2
D.y=a+a(1+x)+a(1+x)2
6.据省统计局公布的数据,安徽省2020年第二季度GDP总值约为7.9千亿元人民币,若我省第四季度GDP总值为y千亿元人民币,平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是( )
A.y=7.9(1+2x)
B.y=7.9(1﹣x)2
C.y=7.9(1+x)2
D.y=7.9+7.9(1+x)+7.9(1+x)2
7.小明准备画一个二次函数的图象,他首先列表(如下表),但在填写函数值时,不小心把其中一个蘸上了墨水(表中),那么这个被蘸上了墨水的函数值是( )
x
…
﹣1
0
1
2
3
…
y
…
3
4
3
0
…
A.﹣1
B.3
C.4
D.0
8.已知某种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h=﹣t2+20t+1.若此礼炮在升空到最高处时引爆,则引爆需要的时间为( )
A.3s
B.4s
C.5s
D.6s
9.下列图形中,阴影部分面积为1的是( )
A.
B.
C.
D.
10.将进货价格为35元的商品按单价40元售出时,能卖出200个,已知该商品单价每上涨2元,其销售量就减少10个.设这种商品的售价为x元时,获得的利润为y元,则下列关系式正确的是( )
A.y=(x﹣35)(400﹣5x)
B.y=(x﹣35)(600﹣10x)
C.y=(x+5)(200﹣5x)
D.y=(x+5)(200﹣10x)
11.若二次函数y=kx2﹣2x﹣1与x轴有交点,则k的取值范围是( )
A.k>﹣1
B.k≤1且k≠0
C.k<﹣1
D.k≥﹣1且k≠0
12.如表格中是二次函数y=ax2+bx+c(a≠0)的自变量x与函数y的一些对应值,可以判断方程ax2+bx+c=﹣3(a≠0)的一个近似根是( )
x
﹣1.1
﹣1.2
﹣1.3
﹣1.4
y=ax2+bx+c
﹣2.75
﹣2.86
﹣3.13
﹣3.28
A.﹣1.1
B.﹣1.2
C.﹣1.3
D.﹣1.4
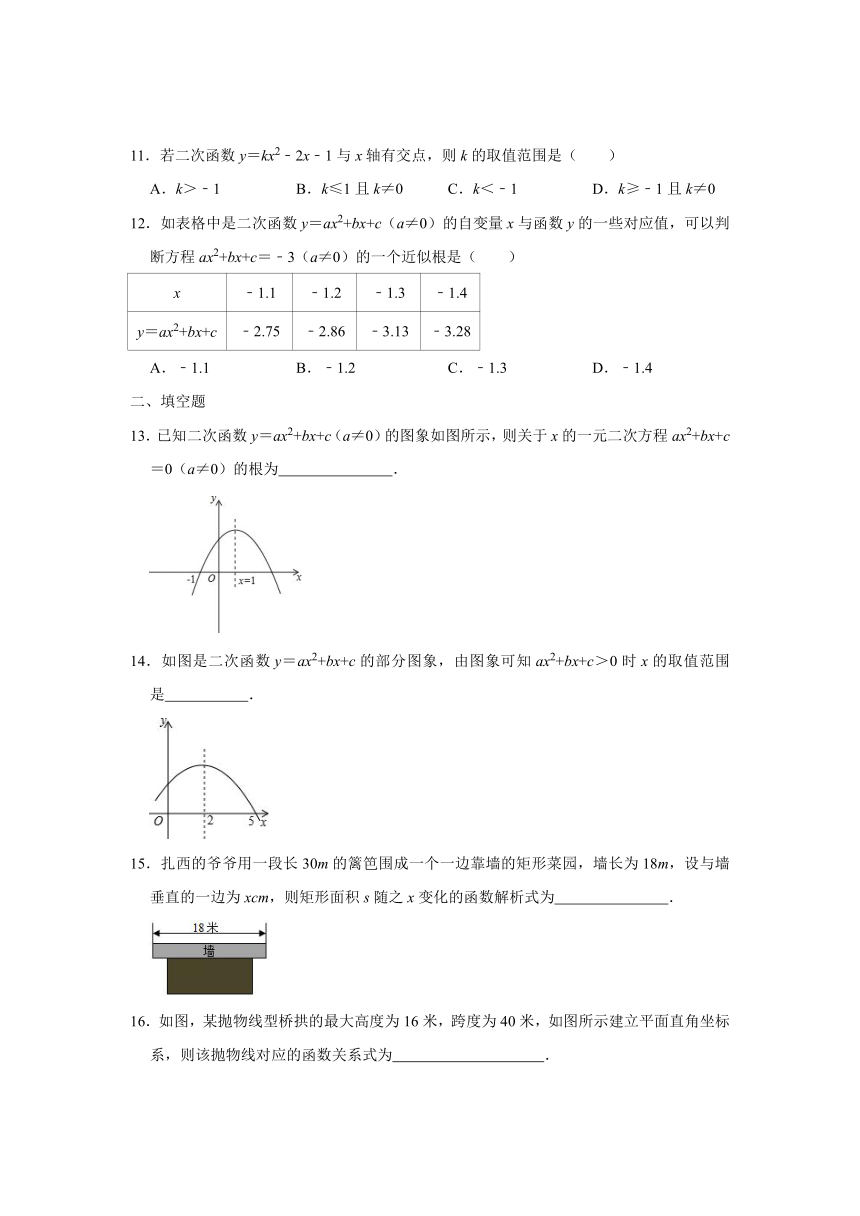
二、填空题
13.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则关于x的一元二次方程ax2+bx+c=0(a≠0)的根为
.
14.如图是二次函数y=ax2+bx+c的部分图象,由图象可知ax2+bx+c>0时x的取值范围是
.
15.扎西的爷爷用一段长30m的篱笆围成一个一边靠墙的矩形菜园,墙长为18m,设与墙垂直的一边为xcm,则矩形面积s随之x变化的函数解析式为
.
16.如图,某抛物线型桥拱的最大高度为16米,跨度为40米,如图所示建立平面直角坐标系,则该抛物线对应的函数关系式为
.
17.已知二次函数y=x2与一次函数y=2x+1相交于A、B两点,点C是线段AB上一动点,点D是抛物线上一动点,且CD平行于y轴,在移动过程中CD最大值为
.
18.下列关于二次函数y=x2﹣(m+1)x+m(m为常数)的结论:①该函数图象是开口向上的抛物线;②该函数图象一定经过点(1,0);③该函数图象与x轴有两个公共点;④该函数图象的顶点在函数y=﹣(x﹣1)2的图象上.其中所有正确结论的序号是
.
三、解答题
19.已知关于x的一元二次方程x2+x﹣m=0.
(1)若方程有两个不相等的实数根,求m的取值范围;
(2)二次函数y=x2+x﹣m的部分图象如图所示,求一元二次方程x2+x﹣m=0的解.
20.如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B,且当x=4时,二次函数的值为6.
(1)求m的值和抛物线的解析式;
(2)求不等式x2+bx+c>x+m的解集.
参考答案
1.解:令y=0,则kx2﹣6x﹣9=0.
∵二次函数y=kx2﹣6x﹣9的图象与x轴有两个不同的交点,
∴一元二次方程kx2﹣6x﹣9=0有两个不相等的解,
∴,
解得:k>﹣1且k≠0.
故选:B.
2.解:由表格中的数据看出﹣0.01和0.02更接近于0,
故x应取对应的范围为:6.18<x<6.19,
故选:C.
3.解:将点A(﹣2,4)代入y1=﹣x+k,
∴k=2,
再将点A(﹣2,4)代入y2=ax2,
∴a=1,
∴y=﹣x+2与y=x2交于两点,
∴B(1,1),
∴y1<y2时,x<﹣2或x>1;
故选:C.
4.解:当y1<y2,则x的取值范围为﹣1<x<4.
故选:C.
5.解:根据题意,得:y关于x的函数关系式为y=a(1+x)2,
故选:C.
6.解:设平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是:y=7.9(1+x)2.
故选:C.
7.解:∵x=0、x=2时的函数值都是3相等,
∴此函数图象的对称轴为直线x==1.
∴这个被蘸上了墨水的函数值是0,
故选:D.
8.解:∵h=﹣t2+20t+1,
∴h=﹣(t﹣4)2+41,
∴顶点坐标为(4,41),
∴到达最高处的时间为4s.
故选:B.
9.解:A、该抛物线与坐标轴交于:(﹣1,0),(1,0),(0,﹣1),故阴影部分的三角形是等腰直角三角形,其面积S=×2×1=1;
B、该抛物线与坐标轴交于:(0,0),(1,0),顶点坐标为(﹣,1),故阴影部分的三角形是等腰直角三角形,其面积S=×1×1=;
C、该抛物线与坐标轴交于:(0,0),(2,0),顶点坐标为(0,﹣2),故阴影部分的三角形是等腰直角三角形,其面积S=×2×2=2;
D、该抛物线与坐标轴交于:(﹣,0),(,0),(0,2),故阴影部分的三角形是等腰直角三角形,其面积S=×2×2=2;
故选:A.
10.解:设这种商品的售价为x元时,获得的利润为y元,根据题意可得:y=(x﹣35)(400﹣5x),
故选:A.
11.解:∵二次函数y=kx2﹣2x﹣l与x轴有交点,
∴△=(﹣2)2﹣4k×(﹣1)≥0,且k≠0,
解得k≥﹣1且k≠0,
故选:D.
12.解:由题意,得
y=ax2+x+c+3对应的值x=﹣1.1,y=0.25;
x=﹣1.2,y=0.14;
x=﹣1.3,y=﹣0.13;
x=﹣1.4,y=﹣0.28,
由此可得x=﹣1.3时,y值更接近0,
ax2+bx+c=﹣3(a≠0)的一个近似根是x=﹣1.3,
故选:C.
13.解:根据图象知,抛物线y=ax2+bx+c(a≠0)与x轴的一个交点是(﹣1,0),对称轴是直线x=1.
设该抛物线与x轴的另一个交点是(x,0).则
=1,
解得,x=3,
即该抛物线与x轴的另一个交点是(3,0).
所以关于x的一元二次方程ax2+bx+c=0(a≠0)的根为x1=﹣1,x2=3.
故答案是:x1=﹣1,x2=3.
14.解:由图可知,二次函数图象为直线x=2,
所以,函数图象与x轴的另一交点为(﹣1,0),
所以,ax2+bx+c>0时x的取值范围是﹣1<x<5.
故答案为:﹣1<x<5.
15.解:由题意可得,
s=x(30﹣2x)=﹣2x2+30x,
故答案为:s=﹣2x2+30x
16.解:由图象可知抛物线顶点坐标(20,16),经过(0,0),(40,0).
设抛物线的解析式为y=a(x﹣20)2+16,把(0,0)代入得到a=﹣,
∴抛物线的解析式为y=﹣(x﹣20)2+16,
即y=﹣x2+x,
故答案为:y=﹣x2+x.
17.解:根据题意得,CD=2x+1﹣x2=﹣x2+2x+1=﹣(x2﹣2x+1﹣1)+1=﹣(x2﹣2x+1)+2=﹣(x﹣1)2+2,
可见CD的最大值为2.
故答案为2.
18.解:①抛物线系数a=1,
∴开口向上正确;
②当x=1时代入抛物线解析式y=12﹣(m+1)×1+m=0,
∴该函数图象一定经过点(1,0)正确;
③令x2﹣(m+1)x+m=0,
△=(m+1)2﹣4m=(m﹣1)2,
当m=1时该函数图象与x轴只有一个公共点,
故该函数图象与x轴有两个公共点不正确;
④∵y=x2﹣(m+1)x+m=(x﹣)2+,
∴二次函数y=x2﹣(m+1)x+m(m为常数)的顶点坐标为(,),
又∵=﹣=﹣(﹣1)2,
∴函数图象的顶点在函数y=﹣(x﹣1)2的图象上正确,
故答案为①②④.
19.解:(1)∵一元二次方程x2+x﹣m=0有两个不相等的实数根,
∴△>0,即1+4m>0,
∴m>﹣;
(2)二次函数y=x2+x﹣m图象的对称轴为直线x=﹣,
∴抛物线与x轴两个交点关于直线x=﹣对称,
由图可知抛物线与x轴一个交点为(1,0),
∴另一个交点为(﹣2,0),
∴一元二次方程x2+x﹣m=0的解为x1=1,x2=﹣2.
20.解:(1)∵直线y=x+m经过点A(1,0),
∴1+m=0,解得m=﹣1;
∵抛物线y=x2+bx+c经过点A(1,0),且当x=4时,二次函数的值为6,
∴,解得,
∴抛物线的解析式为y=x2﹣3x+2;
(2)∵由(1)知m=﹣1,抛物线的解析式为y=x2﹣3x+2,
∴直线的解析式为y=x﹣1,
∴,解得或,
∴B(3,2).
∵由函数图象可知,当x<1或x>3时,二次函数的值大于一次函数的值,
∴不等式x2+bx+c>x+m的解集为x<1或x>3.
一、选择题
1.已知二次函数y=kx2﹣6x﹣9的图象与x轴有两个不同的交点,则k的取值范围为( )
A.k>﹣1
B.k>﹣1且k≠0
C.k≥﹣1
D.k≥﹣1且k≠0
2.二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表,则方程ax2+bx+c=0的一个解的范围是( )
x
6.17
6.18
6.19
y
﹣0.03
﹣0.01
0.02
A.﹣0.03<x<﹣0.01
B.﹣0.01<x<0.02
C.6.18<x<6.19
D.6.17<x<6.18
3.如图,直线y1=﹣x+k与抛物线y2=ax2(a≠0)交于点A(﹣2,4)和点B.若y1<y2,则x的取值范围是( )
A.x<﹣2
B.﹣2<x<1
C.x<﹣2或x>1
D.x<﹣2或x>
4.如图,直线y1=kx+b与抛物线y2=ax2+bx+c交于A(﹣1,m)、B(4,n)两点,若y1<y2,则x的取值范围( )
A.x<﹣1
B.x>4
C.﹣1<x<4
D.x<﹣1或x>4
5.某工厂2019年产品的产量为a吨,该产品产量的年平均增长率为x(x>0),设2021年该产品的产量为y吨,则y关于x的函数关系式为( )
A.y=a(1﹣x)2
B.y=
C.y=a(1+x)2
D.y=a+a(1+x)+a(1+x)2
6.据省统计局公布的数据,安徽省2020年第二季度GDP总值约为7.9千亿元人民币,若我省第四季度GDP总值为y千亿元人民币,平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是( )
A.y=7.9(1+2x)
B.y=7.9(1﹣x)2
C.y=7.9(1+x)2
D.y=7.9+7.9(1+x)+7.9(1+x)2
7.小明准备画一个二次函数的图象,他首先列表(如下表),但在填写函数值时,不小心把其中一个蘸上了墨水(表中),那么这个被蘸上了墨水的函数值是( )
x
…
﹣1
0
1
2
3
…
y
…
3
4
3
0
…
A.﹣1
B.3
C.4
D.0
8.已知某种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h=﹣t2+20t+1.若此礼炮在升空到最高处时引爆,则引爆需要的时间为( )
A.3s
B.4s
C.5s
D.6s
9.下列图形中,阴影部分面积为1的是( )
A.
B.
C.
D.
10.将进货价格为35元的商品按单价40元售出时,能卖出200个,已知该商品单价每上涨2元,其销售量就减少10个.设这种商品的售价为x元时,获得的利润为y元,则下列关系式正确的是( )
A.y=(x﹣35)(400﹣5x)
B.y=(x﹣35)(600﹣10x)
C.y=(x+5)(200﹣5x)
D.y=(x+5)(200﹣10x)
11.若二次函数y=kx2﹣2x﹣1与x轴有交点,则k的取值范围是( )
A.k>﹣1
B.k≤1且k≠0
C.k<﹣1
D.k≥﹣1且k≠0
12.如表格中是二次函数y=ax2+bx+c(a≠0)的自变量x与函数y的一些对应值,可以判断方程ax2+bx+c=﹣3(a≠0)的一个近似根是( )
x
﹣1.1
﹣1.2
﹣1.3
﹣1.4
y=ax2+bx+c
﹣2.75
﹣2.86
﹣3.13
﹣3.28
A.﹣1.1
B.﹣1.2
C.﹣1.3
D.﹣1.4
二、填空题
13.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则关于x的一元二次方程ax2+bx+c=0(a≠0)的根为
.
14.如图是二次函数y=ax2+bx+c的部分图象,由图象可知ax2+bx+c>0时x的取值范围是
.
15.扎西的爷爷用一段长30m的篱笆围成一个一边靠墙的矩形菜园,墙长为18m,设与墙垂直的一边为xcm,则矩形面积s随之x变化的函数解析式为
.
16.如图,某抛物线型桥拱的最大高度为16米,跨度为40米,如图所示建立平面直角坐标系,则该抛物线对应的函数关系式为
.
17.已知二次函数y=x2与一次函数y=2x+1相交于A、B两点,点C是线段AB上一动点,点D是抛物线上一动点,且CD平行于y轴,在移动过程中CD最大值为
.
18.下列关于二次函数y=x2﹣(m+1)x+m(m为常数)的结论:①该函数图象是开口向上的抛物线;②该函数图象一定经过点(1,0);③该函数图象与x轴有两个公共点;④该函数图象的顶点在函数y=﹣(x﹣1)2的图象上.其中所有正确结论的序号是
.
三、解答题
19.已知关于x的一元二次方程x2+x﹣m=0.
(1)若方程有两个不相等的实数根,求m的取值范围;
(2)二次函数y=x2+x﹣m的部分图象如图所示,求一元二次方程x2+x﹣m=0的解.
20.如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B,且当x=4时,二次函数的值为6.
(1)求m的值和抛物线的解析式;
(2)求不等式x2+bx+c>x+m的解集.
参考答案
1.解:令y=0,则kx2﹣6x﹣9=0.
∵二次函数y=kx2﹣6x﹣9的图象与x轴有两个不同的交点,
∴一元二次方程kx2﹣6x﹣9=0有两个不相等的解,
∴,
解得:k>﹣1且k≠0.
故选:B.
2.解:由表格中的数据看出﹣0.01和0.02更接近于0,
故x应取对应的范围为:6.18<x<6.19,
故选:C.
3.解:将点A(﹣2,4)代入y1=﹣x+k,
∴k=2,
再将点A(﹣2,4)代入y2=ax2,
∴a=1,
∴y=﹣x+2与y=x2交于两点,
∴B(1,1),
∴y1<y2时,x<﹣2或x>1;
故选:C.
4.解:当y1<y2,则x的取值范围为﹣1<x<4.
故选:C.
5.解:根据题意,得:y关于x的函数关系式为y=a(1+x)2,
故选:C.
6.解:设平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是:y=7.9(1+x)2.
故选:C.
7.解:∵x=0、x=2时的函数值都是3相等,
∴此函数图象的对称轴为直线x==1.
∴这个被蘸上了墨水的函数值是0,
故选:D.
8.解:∵h=﹣t2+20t+1,
∴h=﹣(t﹣4)2+41,
∴顶点坐标为(4,41),
∴到达最高处的时间为4s.
故选:B.
9.解:A、该抛物线与坐标轴交于:(﹣1,0),(1,0),(0,﹣1),故阴影部分的三角形是等腰直角三角形,其面积S=×2×1=1;
B、该抛物线与坐标轴交于:(0,0),(1,0),顶点坐标为(﹣,1),故阴影部分的三角形是等腰直角三角形,其面积S=×1×1=;
C、该抛物线与坐标轴交于:(0,0),(2,0),顶点坐标为(0,﹣2),故阴影部分的三角形是等腰直角三角形,其面积S=×2×2=2;
D、该抛物线与坐标轴交于:(﹣,0),(,0),(0,2),故阴影部分的三角形是等腰直角三角形,其面积S=×2×2=2;
故选:A.
10.解:设这种商品的售价为x元时,获得的利润为y元,根据题意可得:y=(x﹣35)(400﹣5x),
故选:A.
11.解:∵二次函数y=kx2﹣2x﹣l与x轴有交点,
∴△=(﹣2)2﹣4k×(﹣1)≥0,且k≠0,
解得k≥﹣1且k≠0,
故选:D.
12.解:由题意,得
y=ax2+x+c+3对应的值x=﹣1.1,y=0.25;
x=﹣1.2,y=0.14;
x=﹣1.3,y=﹣0.13;
x=﹣1.4,y=﹣0.28,
由此可得x=﹣1.3时,y值更接近0,
ax2+bx+c=﹣3(a≠0)的一个近似根是x=﹣1.3,
故选:C.
13.解:根据图象知,抛物线y=ax2+bx+c(a≠0)与x轴的一个交点是(﹣1,0),对称轴是直线x=1.
设该抛物线与x轴的另一个交点是(x,0).则
=1,
解得,x=3,
即该抛物线与x轴的另一个交点是(3,0).
所以关于x的一元二次方程ax2+bx+c=0(a≠0)的根为x1=﹣1,x2=3.
故答案是:x1=﹣1,x2=3.
14.解:由图可知,二次函数图象为直线x=2,
所以,函数图象与x轴的另一交点为(﹣1,0),
所以,ax2+bx+c>0时x的取值范围是﹣1<x<5.
故答案为:﹣1<x<5.
15.解:由题意可得,
s=x(30﹣2x)=﹣2x2+30x,
故答案为:s=﹣2x2+30x
16.解:由图象可知抛物线顶点坐标(20,16),经过(0,0),(40,0).
设抛物线的解析式为y=a(x﹣20)2+16,把(0,0)代入得到a=﹣,
∴抛物线的解析式为y=﹣(x﹣20)2+16,
即y=﹣x2+x,
故答案为:y=﹣x2+x.
17.解:根据题意得,CD=2x+1﹣x2=﹣x2+2x+1=﹣(x2﹣2x+1﹣1)+1=﹣(x2﹣2x+1)+2=﹣(x﹣1)2+2,
可见CD的最大值为2.
故答案为2.
18.解:①抛物线系数a=1,
∴开口向上正确;
②当x=1时代入抛物线解析式y=12﹣(m+1)×1+m=0,
∴该函数图象一定经过点(1,0)正确;
③令x2﹣(m+1)x+m=0,
△=(m+1)2﹣4m=(m﹣1)2,
当m=1时该函数图象与x轴只有一个公共点,
故该函数图象与x轴有两个公共点不正确;
④∵y=x2﹣(m+1)x+m=(x﹣)2+,
∴二次函数y=x2﹣(m+1)x+m(m为常数)的顶点坐标为(,),
又∵=﹣=﹣(﹣1)2,
∴函数图象的顶点在函数y=﹣(x﹣1)2的图象上正确,
故答案为①②④.
19.解:(1)∵一元二次方程x2+x﹣m=0有两个不相等的实数根,
∴△>0,即1+4m>0,
∴m>﹣;
(2)二次函数y=x2+x﹣m图象的对称轴为直线x=﹣,
∴抛物线与x轴两个交点关于直线x=﹣对称,
由图可知抛物线与x轴一个交点为(1,0),
∴另一个交点为(﹣2,0),
∴一元二次方程x2+x﹣m=0的解为x1=1,x2=﹣2.
20.解:(1)∵直线y=x+m经过点A(1,0),
∴1+m=0,解得m=﹣1;
∵抛物线y=x2+bx+c经过点A(1,0),且当x=4时,二次函数的值为6,
∴,解得,
∴抛物线的解析式为y=x2﹣3x+2;
(2)∵由(1)知m=﹣1,抛物线的解析式为y=x2﹣3x+2,
∴直线的解析式为y=x﹣1,
∴,解得或,
∴B(3,2).
∵由函数图象可知,当x<1或x>3时,二次函数的值大于一次函数的值,
∴不等式x2+bx+c>x+m的解集为x<1或x>3.
同课章节目录
