1.3证明课时练习 2021—2022学年浙教版数学八年级上册 (Word版 含答案)
文档属性
| 名称 | 1.3证明课时练习 2021—2022学年浙教版数学八年级上册 (Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 157.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 22:44:42 | ||
图片预览

文档简介
浙教版数学八年级上册1.3
《证明》课时练习
一、选择题
1.如图,已知AB∥CD,BC平分∠ABE,∠C=33°,则∠BED的度数是(
)
A.16°
B.33°
C.49°
D.66°
2.如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是(
)
A.30°
B.20°
C.15°
D.14°
3.如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°,则∠AOF的度数是( )
A.20°?
??
B.25°??
???
C.30°???
??
D.35°
4.如图,直线AB与CD相交于E,在∠CEB的平分线上有一点F,FM∥AB.当∠3=10°时,∠F度数是( )
A.80°
B.82°
C.83°
D.85°
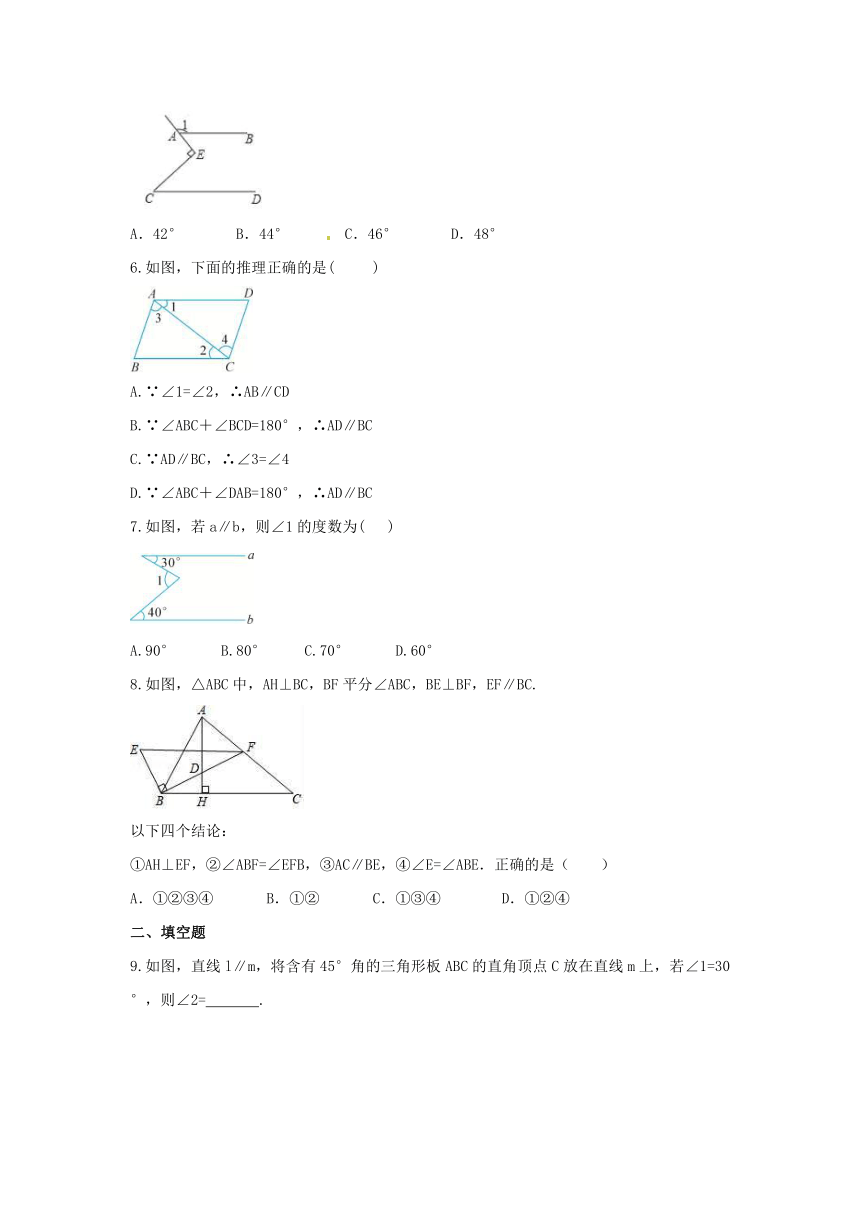
5.如图,直线AB∥CD,∠1=136°,∠E为直角,则∠C等于( )
A.42°
B.44°
C.46°
D.48°
6.如图,下面的推理正确的是(
)
A.∵∠1=∠2,∴AB∥CD
B.∵∠ABC+∠BCD=180°,∴AD∥BC
C.∵AD∥BC,∴∠3=∠4
D.∵∠ABC+∠DAB=180°,∴AD∥BC
7.如图,若a∥b,则∠1的度数为(
)
A.90°
B.80°
C.70°
D.60°
8.如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC.
以下四个结论:
①AH⊥EF,②∠ABF=∠EFB,③AC∥BE,④∠E=∠ABE.正确的是( )
A.①②③④
B.①②
C.①③④
D.①②④
二、填空题
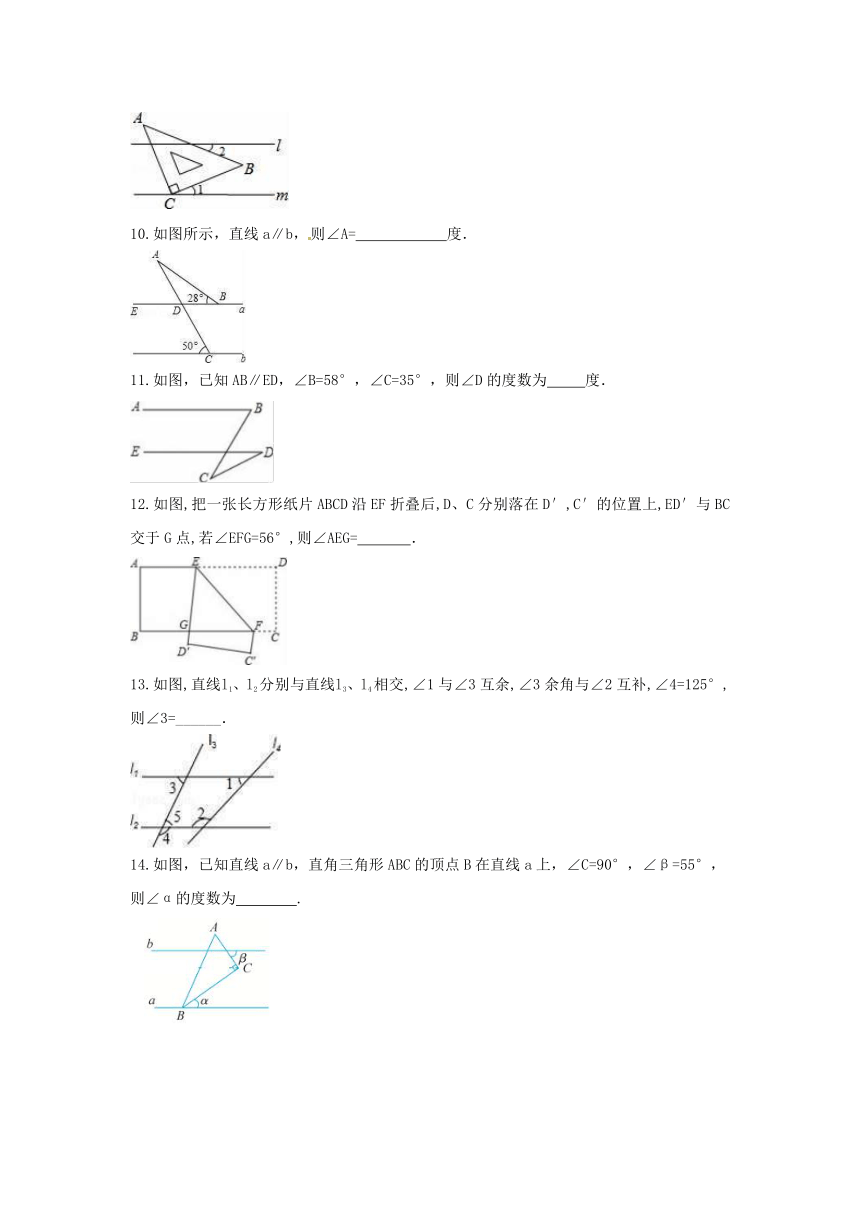
9.如图,直线l∥m,将含有45°角的三角形板ABC的直角顶点C放在直线m上,若∠1=30°,则∠2=
.
10.如图所示,直线a∥b,则∠A= 度.
11.如图,已知AB∥ED,∠B=58°,∠C=35°,则∠D的度数为
度.
12.如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别落在D′,C′的位置上,ED′与BC交于G点,若∠EFG=56°,则∠AEG=
.
13.如图,直线l1、l2分别与直线l3、l4相交,∠1与∠3互余,∠3余角与∠2互补,∠4=125°,
则∠3=______.
14.如图,已知直线a∥b,直角三角形ABC的顶点B在直线a上,∠C=90°,∠β=55°,
则∠α的度数为
.
三、解答题
15.如图,直线a∥b,三角形纸板的直角顶点A落在直线a上,两条直线分别交直线b于B,C两点.若∠1=42°,求∠2的度数.
16.如图,AB∥DE,∠1=∠ACB,AC平分∠BAD,
(1)试说明:
AD∥BC.
(2)若∠B=80°,求∠ADE的度数.
17.如图,已知AB∥CD∥EF,GC⊥CF,∠ABC=65?,∠EFC=40?,求∠BCG的度数。
18.如图,已知AB∥CD,分别探讨下面四个图形中∠APC与∠PAB,∠PCD之间的关系,请你从所得到的关系中任选一个加以证明。
(1)在图1中,∠APC与∠PAB,∠PCD之间的关系是:
.
(2)在图2中,∠APC与∠PAB,∠PCD之间的关系是:
.
(3)在图3中,∠APC与∠PAB,∠PCD之间的关系是:
.
(4)在图4中,∠APC与∠PAB,∠PCD之间的关系是:
.
(5)在图
中,求证:
.
参考答案
1.D.
2.C
3.D.
4.D.
5.C.
6.D.
7.C.
8.D.
解析:∵AH⊥BC,EF∥BC,∴①AH⊥EF正确;
∵BF平分∠ABC,∴∠ABF=∠CBF,∵EF∥BC,∴∠EFB=∠CBF,∴②∠ABF=∠EFB正确;
∵BE⊥BF,而AC与BF不一定垂直,∴BE∥AC不一定成立,故③错误;
∵BE⊥BF,∴∠E和∠EFB互余,∠ABE和∠ABF互余,而∠EFB=∠ABF,
∴④∠E=∠ABE正确.故选:D.
9.答案为:15°.
10.答案为:22;
11.答案为:23.
12.答案为:68°
13.答案为:55°.
14.答案为:35°.
15.解:∵直线a∥b,∠1=42°(已知),
∴∠ACB=42°(两直线平行,内错角相等).
又∵∠BAC=90°(已知),
∴∠ABC=180°-∠BAC-∠ACB=48°(三角形的内角和为180°),
∴∠2=∠ABC=48°(对顶角相等).
16.(1)证明:∵AB∥DE(已知),
∴∠1=∠BAC(两直线平行,同位角相等),
∵AC平分∠BAD(已知),
∴∠BAC=∠DAC,
∴∠1=∠DAC(等量代换),
∵∠1=∠ACB(已知),
∴∠DAC=∠ACB(等量代换),
∴AD∥BC(内错角相等,两直线平行).
(2)证明:∵AB∥CD,AD∥BC,
∴∠B=∠DEC,∠DEC=∠ADE,
∴∠B=∠ADE,
∵∠B=80°,
∴∠ADE=80°.
17.答案为:15°.
18.解:(1)∠APC+∠PAB+∠PCD=360°;
(2)∠APC=∠PAB+∠PCD;
(3)∠PAB=∠APC+∠PCD;
(4)∠PCD=∠APC+∠PAB.
(5)在图2中,求证:∠APC=∠PAB+∠PCD.
证明:过P点作PE∥AB,
∴∠1=∠PAB.
又∵AB∥CD,PE∥CD,
∴∠2=∠PCD,
∴∠1+∠2=∠PAB+∠PCD,
而∠APC=∠1+∠2,
∴∠APC=∠PAB+∠PCD.
《证明》课时练习
一、选择题
1.如图,已知AB∥CD,BC平分∠ABE,∠C=33°,则∠BED的度数是(
)
A.16°
B.33°
C.49°
D.66°
2.如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是(
)
A.30°
B.20°
C.15°
D.14°
3.如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°,则∠AOF的度数是( )
A.20°?
??
B.25°??
???
C.30°???
??
D.35°
4.如图,直线AB与CD相交于E,在∠CEB的平分线上有一点F,FM∥AB.当∠3=10°时,∠F度数是( )
A.80°
B.82°
C.83°
D.85°
5.如图,直线AB∥CD,∠1=136°,∠E为直角,则∠C等于( )
A.42°
B.44°
C.46°
D.48°
6.如图,下面的推理正确的是(
)
A.∵∠1=∠2,∴AB∥CD
B.∵∠ABC+∠BCD=180°,∴AD∥BC
C.∵AD∥BC,∴∠3=∠4
D.∵∠ABC+∠DAB=180°,∴AD∥BC
7.如图,若a∥b,则∠1的度数为(
)
A.90°
B.80°
C.70°
D.60°
8.如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC.
以下四个结论:
①AH⊥EF,②∠ABF=∠EFB,③AC∥BE,④∠E=∠ABE.正确的是( )
A.①②③④
B.①②
C.①③④
D.①②④
二、填空题
9.如图,直线l∥m,将含有45°角的三角形板ABC的直角顶点C放在直线m上,若∠1=30°,则∠2=
.
10.如图所示,直线a∥b,则∠A= 度.
11.如图,已知AB∥ED,∠B=58°,∠C=35°,则∠D的度数为
度.
12.如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别落在D′,C′的位置上,ED′与BC交于G点,若∠EFG=56°,则∠AEG=
.
13.如图,直线l1、l2分别与直线l3、l4相交,∠1与∠3互余,∠3余角与∠2互补,∠4=125°,
则∠3=______.
14.如图,已知直线a∥b,直角三角形ABC的顶点B在直线a上,∠C=90°,∠β=55°,
则∠α的度数为
.
三、解答题
15.如图,直线a∥b,三角形纸板的直角顶点A落在直线a上,两条直线分别交直线b于B,C两点.若∠1=42°,求∠2的度数.
16.如图,AB∥DE,∠1=∠ACB,AC平分∠BAD,
(1)试说明:
AD∥BC.
(2)若∠B=80°,求∠ADE的度数.
17.如图,已知AB∥CD∥EF,GC⊥CF,∠ABC=65?,∠EFC=40?,求∠BCG的度数。
18.如图,已知AB∥CD,分别探讨下面四个图形中∠APC与∠PAB,∠PCD之间的关系,请你从所得到的关系中任选一个加以证明。
(1)在图1中,∠APC与∠PAB,∠PCD之间的关系是:
.
(2)在图2中,∠APC与∠PAB,∠PCD之间的关系是:
.
(3)在图3中,∠APC与∠PAB,∠PCD之间的关系是:
.
(4)在图4中,∠APC与∠PAB,∠PCD之间的关系是:
.
(5)在图
中,求证:
.
参考答案
1.D.
2.C
3.D.
4.D.
5.C.
6.D.
7.C.
8.D.
解析:∵AH⊥BC,EF∥BC,∴①AH⊥EF正确;
∵BF平分∠ABC,∴∠ABF=∠CBF,∵EF∥BC,∴∠EFB=∠CBF,∴②∠ABF=∠EFB正确;
∵BE⊥BF,而AC与BF不一定垂直,∴BE∥AC不一定成立,故③错误;
∵BE⊥BF,∴∠E和∠EFB互余,∠ABE和∠ABF互余,而∠EFB=∠ABF,
∴④∠E=∠ABE正确.故选:D.
9.答案为:15°.
10.答案为:22;
11.答案为:23.
12.答案为:68°
13.答案为:55°.
14.答案为:35°.
15.解:∵直线a∥b,∠1=42°(已知),
∴∠ACB=42°(两直线平行,内错角相等).
又∵∠BAC=90°(已知),
∴∠ABC=180°-∠BAC-∠ACB=48°(三角形的内角和为180°),
∴∠2=∠ABC=48°(对顶角相等).
16.(1)证明:∵AB∥DE(已知),
∴∠1=∠BAC(两直线平行,同位角相等),
∵AC平分∠BAD(已知),
∴∠BAC=∠DAC,
∴∠1=∠DAC(等量代换),
∵∠1=∠ACB(已知),
∴∠DAC=∠ACB(等量代换),
∴AD∥BC(内错角相等,两直线平行).
(2)证明:∵AB∥CD,AD∥BC,
∴∠B=∠DEC,∠DEC=∠ADE,
∴∠B=∠ADE,
∵∠B=80°,
∴∠ADE=80°.
17.答案为:15°.
18.解:(1)∠APC+∠PAB+∠PCD=360°;
(2)∠APC=∠PAB+∠PCD;
(3)∠PAB=∠APC+∠PCD;
(4)∠PCD=∠APC+∠PAB.
(5)在图2中,求证:∠APC=∠PAB+∠PCD.
证明:过P点作PE∥AB,
∴∠1=∠PAB.
又∵AB∥CD,PE∥CD,
∴∠2=∠PCD,
∴∠1+∠2=∠PAB+∠PCD,
而∠APC=∠1+∠2,
∴∠APC=∠PAB+∠PCD.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
