1.2 二次函数的图像习题精练- 2021-2022学年浙教版数学九年级上册(Word版 含答案)
文档属性
| 名称 | 1.2 二次函数的图像习题精练- 2021-2022学年浙教版数学九年级上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 214.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 22:46:22 | ||
图片预览




文档简介
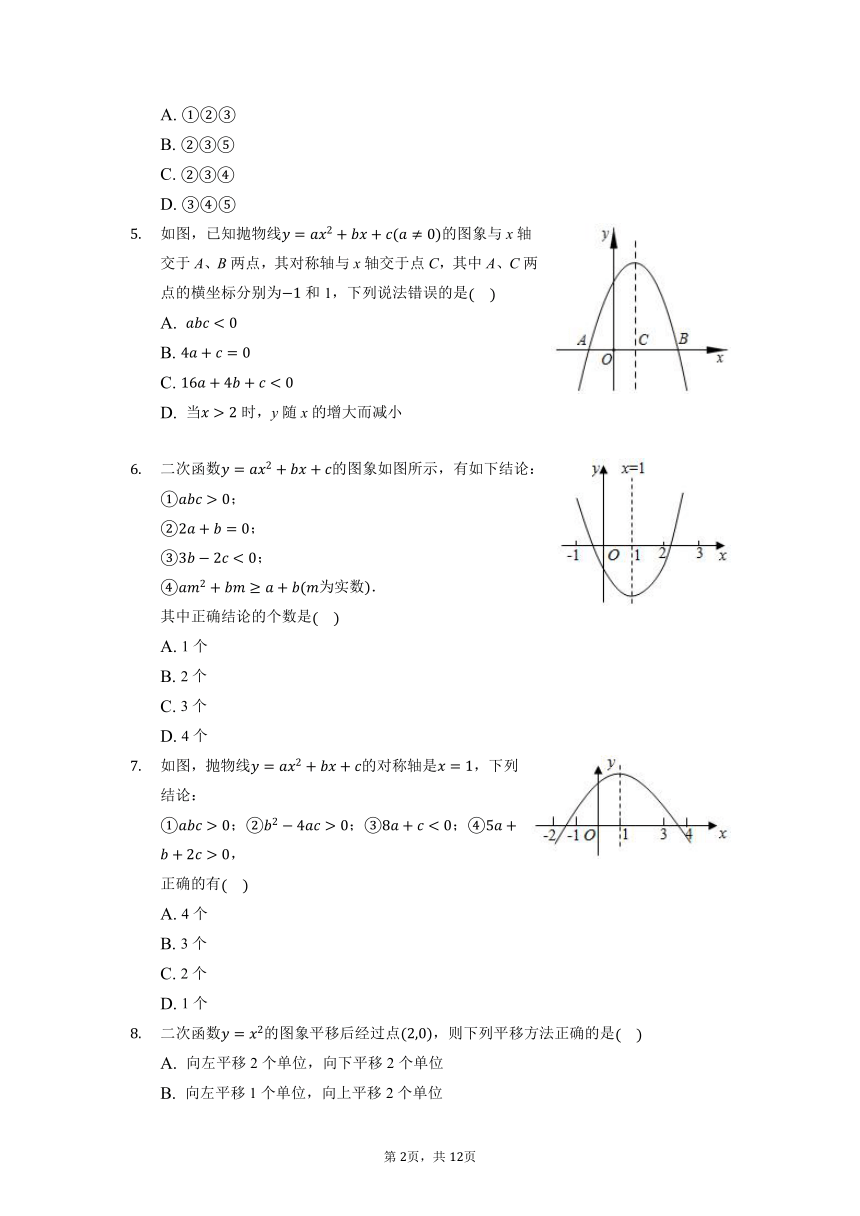
浙教版九年级第一章1.2二次函数的图像习题精练
一、选择题
在同一平面直角坐标系中,一次函数和二次函数的大致图象可能为?
?
A.
B.
C.
D.
如图所示,正方形ABCD的边长为10,四个全等的小正方形的对称中心分别在正方形ABCD的顶点上,且它们的各边与正方形ABCD各边平行或垂直若小正方形的边长为x,且,阴影部分的面积为y,则能反映y与x之间函数关系的大致图象是?
?
A.
B.
C.
D.
以下性质:
开口向上
以点为顶点
以y轴为对称轴
关于x轴对称.
其中是抛物线,,的共同性质的有?
?
A.
1个
B.
2个
C.
3个
D.
4个
如图,已知二次函数的图象如图所示,有下列5个结论:;;;;其中正确结论的有
A.
B.
C.
D.
如图,已知抛物线的图象与x轴交于A、B两点,其对称轴与x轴交于点C,其中A、C两点的横坐标分别为和1,下列说法错误的是
A.
B.
C.
D.
当时,y随x的增大而减小
二次函数的图象如图所示,有如下结论:
;
;
;
为实数.
其中正确结论的个数是
A.
1个
B.
2个
C.
3个
D.
4个
如图,抛物线的对称轴是,下列结论:
;;;,
正确的有
A.
4个
B.
3个
C.
2个
D.
1个
二次函数的图象平移后经过点,则下列平移方法正确的是
A.
向左平移2个单位,向下平移2个单位
B.
向左平移1个单位,向上平移2个单位
C.
向右平移1个单位,向下平移1个单位
D.
向右平移2个单位,向上平移1个单位
抛物线与y轴的交点坐标为?
???
A.
B.
C.
D.
如图,正方形四个顶点的坐标依次为,,,若抛物线的图象与正方形有公共点,则实数a的取值范围是
A.
B.
C.
D.
二、填空题
二次函数图象的顶点所在的图象对应的函数表达式为??????????.
若对于任意非零实数a,抛物线总不经过点,则写出符合条件的点P的坐标:______.
如图所示,已知抛物线,试确定下列各式与0的关系填“”“”或“”??????????0,b??????????0,c??????????0,??????????0,??????????
将抛物线向右平移1单位,得到的抛物线与y轴的交点的坐标是______.
三、解答题
在平面直角坐标系xOy中,抛物线.
求抛物线顶点C的坐标用含m的代数式表示;
已知点,,若该抛物线与线段AB有公共点,结合函数图象,求出m的取值范围.
已知抛物线经过.
求抛物线对应的函数关系式
若将此抛物线沿x轴向右平移,平移后的抛物线经过,求平移距离.
在平面直角坐标系xOy中,抛物线C:的顶点为P.
直接写出点P的坐标用含m的式子表示;
已知点关于直线的对称点为点B,抛物线C与线段AB有公共点.
当时,若点B恰好在抛物线C上,求m的值;
直接写出的取值范围.
将抛物线先向下平移3个单位,再向右平移个单位,所得新抛物线经过点,求新抛物线的表达式及新抛物线与y轴交点的坐标.
答案和解析
1.【答案】B
【解析】解:
A.函数中,,,函数中,,,A错误
B.函数中,,,函数中,,,B正确
C.函数中,,,函数中,,,C错误
D.函数中,,,函数中,,,D错误.
故选B.
2.【答案】D【解析】解:由题意可得,阴影部分的面积相当于一个小正方形的面积,
,
故选D.
3.【答案】B
【解析】解:抛物线,的开口向上,的开口向下
抛物线,,的顶点均为点,对称轴都为y轴,则是这三个抛物线的共同性质.
故选B.
4.【答案】B
【解析】解:由抛物线开口向下可知,
抛物线与y轴交点在x轴上方可知:,
对称轴在y轴的右侧,
即,,
,
故不正确;
当时,,
,
故正确;
由对称知,当时,函数值大于0,
即,
故正确;
,
,
,
,
,
故不正确;
当时,y的值最大,此时,,
而当时,,
所以,
故,即,
故正确.
故正确.
故选:B.??
5.【答案】B
【解析】解:抛物线开口向下,因此,
对称轴为,即,也就是,,
抛物线与y轴交于正半轴,于是,
,因此选项A不符合题意;
由、对称轴为,可得抛物线与x轴的另一个交点,
,,,因此选项B符合题意;
当时,,因此选项C不符合题意;
当时,y随x的增大而减小,因此选项D不符合题意;
故选:B.
6.【答案】D
【解析】解:对称轴在y轴右侧,
、b异号,
,
,故正确;
对称轴,
,故正确;
,
,
当时,,
,故正确;
根据图象知,当时,y有最小值;
当m为实数时,有,
所以为实数,故正确.
本题正确的结论有:,4个;
故选:D.
7.【答案】B
【解析】解:由抛物线的开口向下可得:,
根据抛物线的对称轴在y轴右边可得:a,b异号,所以,
根据抛物线与y轴的交点在正半轴可得:,
,故错误;
抛物线与x轴有两个交点,
,故正确;
直线是抛物线的对称轴,所以,可得,
由图象可知,当时,,即,
,
即,故正确;
由图象可知,当时,;当时,,
两式相加得,,故正确;
结论正确的是,3个,
故选:B.??
8.【答案】C
【解析】解:A、平移后的解析式为,当时,,本选项不符合题意.
B、平移后的解析式为,当时,,本选项不符合题意.
C、平移后的解析式为,当时,,函数图象经过,本选项符合题意.
D、平移后的解析式为,当时,,本选项不符合题意.
故选:C.
9.【答案】D
【解析】解:当时,
抛物线与y轴的交点坐标为?,
故选D.??
10.【答案】A
【解析】解:当抛物线经过时,,
当抛物线经过时,,
观察图象可知,
故选:A.
11.【答案】?
【解析】解:二次函数图象的顶点坐标为,
当时,,
,
把代入,得,
即所求表达式为.
12.【答案】,
【解析】解:对于任意非零实数a,抛物线总不经过点,
或,
点P的坐标为或
故答案为或.
13.【答案】
【解析】解:图象开口向下,
抛物线与y轴的交点在y轴的正半轴上,
抛物线的对称轴为,又,所以
把代入解析式,得
把代入解析式,得.
14.【答案】
【解析】解:抛物线的顶点坐标为,
把点向右平移1个单位得到点的坐标为,
所以平移后抛物线解析式为,
所以得到的抛物线与y轴的交点坐标为.
故答案为.
15.【答案】解:,
抛物线顶点为.
把的坐标代入,
得,
解得??.
把的坐标代入,
得,
即,
解得??或.
结合函数图象可知:或.
16.【答案】解:
把代入,得,解得.
故该抛物线对应的函数关系式为.
设平移距离为,
则抛物线沿x轴向右平移h后得到抛物线.
将代入,得,
解得负值舍去,
即平移距离是.
17.【答案】解:抛物线C:,
,,
点P的坐标是,
点与点B关于直线对称,
点,
点B在抛物线C上,
,
解得:,,
点与点B关于直线对称,
点,
当时,,
解得:,,
,,
抛物线C与线段AB有公共点,如图,
或,
解得:或.
18.【答案】解:平移后,设新抛物线的表达式为,
新抛物线经过点,
将,代入:,
,
,
,.
,
舍去,得到.
新抛物线的表达式为.
与y轴的交点坐标,
设交点为,
将代入到新抛物线中,得到:,
与y轴的交点坐标为.
第2页,共3页
一、选择题
在同一平面直角坐标系中,一次函数和二次函数的大致图象可能为?
?
A.
B.
C.
D.
如图所示,正方形ABCD的边长为10,四个全等的小正方形的对称中心分别在正方形ABCD的顶点上,且它们的各边与正方形ABCD各边平行或垂直若小正方形的边长为x,且,阴影部分的面积为y,则能反映y与x之间函数关系的大致图象是?
?
A.
B.
C.
D.
以下性质:
开口向上
以点为顶点
以y轴为对称轴
关于x轴对称.
其中是抛物线,,的共同性质的有?
?
A.
1个
B.
2个
C.
3个
D.
4个
如图,已知二次函数的图象如图所示,有下列5个结论:;;;;其中正确结论的有
A.
B.
C.
D.
如图,已知抛物线的图象与x轴交于A、B两点,其对称轴与x轴交于点C,其中A、C两点的横坐标分别为和1,下列说法错误的是
A.
B.
C.
D.
当时,y随x的增大而减小
二次函数的图象如图所示,有如下结论:
;
;
;
为实数.
其中正确结论的个数是
A.
1个
B.
2个
C.
3个
D.
4个
如图,抛物线的对称轴是,下列结论:
;;;,
正确的有
A.
4个
B.
3个
C.
2个
D.
1个
二次函数的图象平移后经过点,则下列平移方法正确的是
A.
向左平移2个单位,向下平移2个单位
B.
向左平移1个单位,向上平移2个单位
C.
向右平移1个单位,向下平移1个单位
D.
向右平移2个单位,向上平移1个单位
抛物线与y轴的交点坐标为?
???
A.
B.
C.
D.
如图,正方形四个顶点的坐标依次为,,,若抛物线的图象与正方形有公共点,则实数a的取值范围是
A.
B.
C.
D.
二、填空题
二次函数图象的顶点所在的图象对应的函数表达式为??????????.
若对于任意非零实数a,抛物线总不经过点,则写出符合条件的点P的坐标:______.
如图所示,已知抛物线,试确定下列各式与0的关系填“”“”或“”??????????0,b??????????0,c??????????0,??????????0,??????????
将抛物线向右平移1单位,得到的抛物线与y轴的交点的坐标是______.
三、解答题
在平面直角坐标系xOy中,抛物线.
求抛物线顶点C的坐标用含m的代数式表示;
已知点,,若该抛物线与线段AB有公共点,结合函数图象,求出m的取值范围.
已知抛物线经过.
求抛物线对应的函数关系式
若将此抛物线沿x轴向右平移,平移后的抛物线经过,求平移距离.
在平面直角坐标系xOy中,抛物线C:的顶点为P.
直接写出点P的坐标用含m的式子表示;
已知点关于直线的对称点为点B,抛物线C与线段AB有公共点.
当时,若点B恰好在抛物线C上,求m的值;
直接写出的取值范围.
将抛物线先向下平移3个单位,再向右平移个单位,所得新抛物线经过点,求新抛物线的表达式及新抛物线与y轴交点的坐标.
答案和解析
1.【答案】B
【解析】解:
A.函数中,,,函数中,,,A错误
B.函数中,,,函数中,,,B正确
C.函数中,,,函数中,,,C错误
D.函数中,,,函数中,,,D错误.
故选B.
2.【答案】D【解析】解:由题意可得,阴影部分的面积相当于一个小正方形的面积,
,
故选D.
3.【答案】B
【解析】解:抛物线,的开口向上,的开口向下
抛物线,,的顶点均为点,对称轴都为y轴,则是这三个抛物线的共同性质.
故选B.
4.【答案】B
【解析】解:由抛物线开口向下可知,
抛物线与y轴交点在x轴上方可知:,
对称轴在y轴的右侧,
即,,
,
故不正确;
当时,,
,
故正确;
由对称知,当时,函数值大于0,
即,
故正确;
,
,
,
,
,
故不正确;
当时,y的值最大,此时,,
而当时,,
所以,
故,即,
故正确.
故正确.
故选:B.??
5.【答案】B
【解析】解:抛物线开口向下,因此,
对称轴为,即,也就是,,
抛物线与y轴交于正半轴,于是,
,因此选项A不符合题意;
由、对称轴为,可得抛物线与x轴的另一个交点,
,,,因此选项B符合题意;
当时,,因此选项C不符合题意;
当时,y随x的增大而减小,因此选项D不符合题意;
故选:B.
6.【答案】D
【解析】解:对称轴在y轴右侧,
、b异号,
,
,故正确;
对称轴,
,故正确;
,
,
当时,,
,故正确;
根据图象知,当时,y有最小值;
当m为实数时,有,
所以为实数,故正确.
本题正确的结论有:,4个;
故选:D.
7.【答案】B
【解析】解:由抛物线的开口向下可得:,
根据抛物线的对称轴在y轴右边可得:a,b异号,所以,
根据抛物线与y轴的交点在正半轴可得:,
,故错误;
抛物线与x轴有两个交点,
,故正确;
直线是抛物线的对称轴,所以,可得,
由图象可知,当时,,即,
,
即,故正确;
由图象可知,当时,;当时,,
两式相加得,,故正确;
结论正确的是,3个,
故选:B.??
8.【答案】C
【解析】解:A、平移后的解析式为,当时,,本选项不符合题意.
B、平移后的解析式为,当时,,本选项不符合题意.
C、平移后的解析式为,当时,,函数图象经过,本选项符合题意.
D、平移后的解析式为,当时,,本选项不符合题意.
故选:C.
9.【答案】D
【解析】解:当时,
抛物线与y轴的交点坐标为?,
故选D.??
10.【答案】A
【解析】解:当抛物线经过时,,
当抛物线经过时,,
观察图象可知,
故选:A.
11.【答案】?
【解析】解:二次函数图象的顶点坐标为,
当时,,
,
把代入,得,
即所求表达式为.
12.【答案】,
【解析】解:对于任意非零实数a,抛物线总不经过点,
或,
点P的坐标为或
故答案为或.
13.【答案】
【解析】解:图象开口向下,
抛物线与y轴的交点在y轴的正半轴上,
抛物线的对称轴为,又,所以
把代入解析式,得
把代入解析式,得.
14.【答案】
【解析】解:抛物线的顶点坐标为,
把点向右平移1个单位得到点的坐标为,
所以平移后抛物线解析式为,
所以得到的抛物线与y轴的交点坐标为.
故答案为.
15.【答案】解:,
抛物线顶点为.
把的坐标代入,
得,
解得??.
把的坐标代入,
得,
即,
解得??或.
结合函数图象可知:或.
16.【答案】解:
把代入,得,解得.
故该抛物线对应的函数关系式为.
设平移距离为,
则抛物线沿x轴向右平移h后得到抛物线.
将代入,得,
解得负值舍去,
即平移距离是.
17.【答案】解:抛物线C:,
,,
点P的坐标是,
点与点B关于直线对称,
点,
点B在抛物线C上,
,
解得:,,
点与点B关于直线对称,
点,
当时,,
解得:,,
,,
抛物线C与线段AB有公共点,如图,
或,
解得:或.
18.【答案】解:平移后,设新抛物线的表达式为,
新抛物线经过点,
将,代入:,
,
,
,.
,
舍去,得到.
新抛物线的表达式为.
与y轴的交点坐标,
设交点为,
将代入到新抛物线中,得到:,
与y轴的交点坐标为.
第2页,共3页
同课章节目录
