1.2二次函数的图象 同步能力提升训练 2021-2022学年浙教版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 1.2二次函数的图象 同步能力提升训练 2021-2022学年浙教版九年级数学上册(Word版 含答案) | 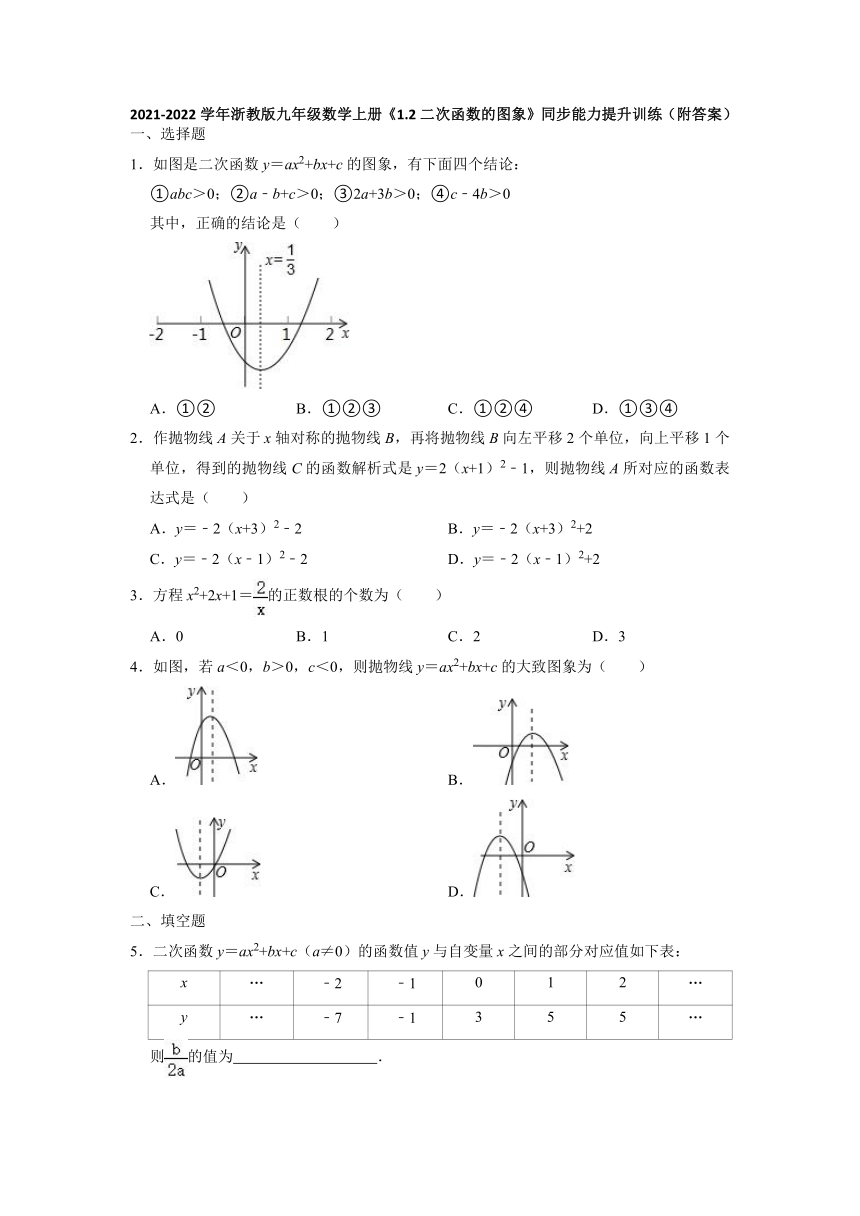 | |
| 格式 | doc | ||
| 文件大小 | 148.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 22:48:00 | ||
图片预览




文档简介
2021-2022学年浙教版九年级数学上册《1.2二次函数的图象》同步能力提升训练(附答案)
一、选择题
1.如图是二次函数y=ax2+bx+c的图象,有下面四个结论:
①abc>0;②a﹣b+c>0;③2a+3b>0;④c﹣4b>0
其中,正确的结论是( )
A.①②
B.①②③
C.①②④
D.①③④
2.作抛物线A关于x轴对称的抛物线B,再将抛物线B向左平移2个单位,向上平移1个单位,得到的抛物线C的函数解析式是y=2(x+1)2﹣1,则抛物线A所对应的函数表达式是( )
A.y=﹣2(x+3)2﹣2
B.y=﹣2(x+3)2+2
C.y=﹣2(x﹣1)2﹣2
D.y=﹣2(x﹣1)2+2
3.方程x2+2x+1=的正数根的个数为( )
A.0
B.1
C.2
D.3
4.如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )
A.
B.
C.
D.
二、填空题
5.二次函数y=ax2+bx+c(a≠0)的函数值y与自变量x之间的部分对应值如下表:
x
…
﹣2
﹣1
0
1
2
…
y
…
﹣7
﹣1
3
5
5
…
则的值为
.
6.已知二次函数y=3(x﹣1)2+k的图象上三点A(2,y1),B(3,y2),C(﹣4,y3),则y1、y2、y3的大小关系是
.
7.已知二次函数y=ax2+bx+c中,自变量x与函数y的部分对应值如下表:
x
…
﹣2
0
2
3
…
y
…
8
0
0
3
…
当x=﹣1时,y=
.
8.若点A(2,m)在抛物线y=x2上,则点A关于原点对称点的坐标是
.
9.已知点A(a,m)、B(b,m)、P(a+b,n)为抛物线y=x2﹣2x﹣2上的点,则n=
.
10.把抛物线y=2x2先向下平移1个单位,再向左平移2个单位,得到的抛物线的解析式是
.
11.已知点A(4,y1),B(,y2),C(﹣2,y3)都在二次函数y=(x﹣2)2﹣m的图象上,则y1,y2,y3的大小关系为
.
12.如图所示,在同一平面直角坐标系中,作出①y=﹣3x2,②y=﹣,③y=﹣x2的图象,则从里到外的三条抛物线对应的函数依次是
(填序号)
13.将抛物线y=x2的图象向上平移1个单位,则平移后的抛物线的解析式为
.
14.将抛物线y=﹣x2向左平移2个单位后,得到的抛物线的解析式是
.
15.若抛物线y=2x2﹣px+4p+1中不管p取何值时都通过定点,则定点坐标为
.
16.已知抛物线y=x2﹣2x+5经过两点A(﹣2,y1)和B(3,y2),则y1与y2的大小关系是
.
17.a、b、c是实数,点A(a+1、b)、B(a+2,c)在二次函数y=x2﹣2ax+3的图象上,则b、c的大小关系是b
c(用“>”或“<”号填空)
三、解答题
18.已知抛物线y=ax2+bx﹣3(a≠0)经过点(﹣1,0),(3,0),求a,b的值.
19.已知抛物线y=a(x﹣3)2+2经过点(1,﹣2).
(1)求a的值;
(2)若点A(m,y1)、B(n,y2)(m<n<3)都在该抛物线上,试比较y1与y2的大小.
20.先阅读以下材料,然后解答问题:
材料:将二次函数y=﹣x2+2x+3的图象向左平移1个单位,再向下平移2个单位,求平移后的抛物线的解析式(平移后抛物线的形状不变).
解:在抛物线y=﹣x2+2x+3图象上任取两点A(0,3)、B(1,4),由题意知:点A向左平移1个单位得到A′(﹣1,3),再向下平移2个单位得到A″(﹣1,1);点B向左平移1个单位得到B′(0,4),再向下平移2个单位得到B″(0,2).
设平移后的抛物线的解析式为y=﹣x2+bx+c.则点A″(﹣1,1),B″(0,2)在抛物线上.可得:,解得:.所以平移后的抛物线的解析式为:y=﹣x2+2.
根据以上信息解答下列问题:
将直线y=2x﹣3向右平移3个单位,再向上平移1个单位,求平移后的直线的解析式.
21.(1)请在坐标系中画出二次函数y=﹣x2+2x的大致图象;
(2)在同一个坐标系中画出y=﹣x2+2x的图象向上平移两个单位后的图象;
(3)直接写出平移后的图象的解析式.
注:图中小正方形网格的边长为1.
22.如图抛物线y=ax2﹣5ax+4a与x轴相交于点A、B,且过点C(5,4).
(1)求a的值和该抛物线顶点P的坐标.
(2)请你设计一种平移的方法,使平移后抛物线的顶点落在第二象限,并写出平移后抛物线的解析式.
参考答案
1.解:∵抛物线开口向上,
∴a>0;
∵抛物线的对称轴在y轴的右侧,
∴x=﹣>0,
∴b<0;
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc>0,所以①正确;
∵x=﹣1时,y>0,
∴a﹣b+c>0,所以②正确;
∵x=﹣=,
∴2a+3b=0,所以③错误;
∵x=2时,y>0,
∴4a+2b+c>0,
把2a=﹣3b代入得﹣6b+2b+c>0,
∴c﹣4b>0,所以④正确.
故选:C.
2.解:易得抛物线C的顶点为(﹣1,﹣1),
∵是向左平移2个单位,向上平移1个单位得到抛物线C的,
∴抛物线B的坐标为(1,﹣2),
可设抛物线B的坐标为y=2(x﹣h)2+k,代入得:y=2(x﹣1)2﹣2,
易得抛物线A的二次项系数为﹣2,顶点坐标为(1,2),
∴抛物线A的解析式为y=﹣2(x﹣1)2+2.
故选:D.
3.解:二次函数y=x2+2x+1=(x+1)2的图象过点(0,1),且在第一、二象限内,
反比例函数y=的图象在第一、三象限,
∴这两个函数只在第一象限有一个交点.
即方程x2+2x+1=的正数根的个数为1.
故选:B.
4.解:∵a<0,
∴抛物线的开口方向向下,
故第三个选项错误;
∵c<0,
∴抛物线与y轴的交点为在y轴的负半轴上,
故第一个选项错误;
∵a<0、b>0,对称轴为x=>0,
∴对称轴在y轴右侧,
故第四个选项错误.
故选:B.
5.解:∵x=1、x=2时的函数值都是﹣1相等,
∴此函数图象的对称轴为直线x=﹣==,
即=﹣.
故答案为:﹣.
6.解:∵y=3(x﹣1)2+k,
∴图象的开口向上,对称轴是直线x=1,
A(﹣4,y3)关于直线x=1的对称点是(6,y3),
∵2<3<6,
∴y1<y2<y3,
故答案为y1<y2<y3.
7.解:依据表格可知抛物线的对称轴为x=1,
∴当x=﹣1时与x=3时函数值相同,
∴当x=﹣1时,y=3.
故答案为:3.
8.解:∵点A(2,m)在抛物线y=x2上,
∴m=4,
∴A(2,4),
∴点A关于原点对称点的坐标是(﹣2,﹣4),
故答案为:(﹣2,﹣4).
9.解:∵抛物线解析式为y=x2﹣2x﹣2=(x﹣1)2﹣3,
∴该抛物线的对称轴是直线x=1,
又∵点A(a,m)和B(b,m)关于直线x=1对称,
∴=1,
∴a+b=2,
把(2,n)代入抛物线的解析式得,n=22﹣2×2﹣2=﹣2.
故答案是:﹣2.
10.解:由“上加下减”的原则可知,二次函数y=2x2的图象向下平移1个单位得到y=2x2﹣1,
由“左加右减”的原则可知,将二次函数y=2x2﹣1的图象向左平移2个单位可得到函数y=2(x+2)2﹣1,
故答案是:y=2(x+2)2﹣1.
11.解:A(4,y1),B(,y2),在对称轴的右侧,y随x的增大而增大,
∵<4,
∴y2<y1,
∴点A离直线x=2近,点C离直线x=2最远,
而抛物线开口向上,
则y3>y1,
故y3>y1>y2,
故答案是:y3>y1>y2.
12.解:①y=﹣3x2,
②y=﹣x2,
③y=﹣x2中,二次项系数a分别为﹣3、﹣、﹣1,
∵|﹣3|>|﹣1|>|﹣|,
∴抛物线②y=﹣x2的开口最宽,抛物线①y=﹣3x2的开口最窄.
故答案为:①③②.
13.解:∵抛物线y=x2的图象向上平移1个单位,
∴平移后的抛物线的解析式为y=x2+1.
故答案为:y=x2+1.
14.解:由“左加右减”的原则可知,抛物线y=﹣x2向左平移2个单位后,得到的抛物线的解析式是y=﹣(x+2)2,即y=﹣x2﹣4x﹣4.
故答案为:y=﹣x2﹣4x﹣4.
15.解:y=2x2﹣px+4p+1可化为y=2x2﹣p(x﹣4)+1,
分析可得:当x=4时,y=33;且与p的取值无关;
故不管p取何值时都通过定点(4,33).
16.解:∵抛物线y=x2﹣2x+5经过两点A(﹣2,y1)和B(3,y2),
∴y1=4+4+5=13,即y1=13,
y2=9﹣6+5=8,即y2=8,
∵8<13,
∴y2<y1.
故答案是:y1>y2.
17.解:∵二次函数y=x2﹣2ax+3的图象的对称轴为x=a,二次项系数1>0,
∴抛物线的开口向上,在对称轴的右边,y随x的增大而增大,
∵a+1<a+2,点A(a+1、b)、B(a+2,c)在二次函数y=x2﹣2ax+3的图象上,
∴b<c,
故答案为:<.
18.解:∵抛物线y=ax2+bx﹣3(a≠0)经过点(﹣1,0),(3,0),
∴,
解得,
,
即a的值是1,b的值是﹣2.
19.解:(1)∵抛物线y=a(x﹣3)2+2经过点(1,﹣2),
∴﹣2=a(1﹣3)2+2,
解得a=﹣1;
(2)∵函数y=﹣(x﹣3)2+2的对称轴为x=3,
∴A(m,y1)、B(n,y2)(m<n<3)在对称轴左侧,
又∵抛物线开口向下,
∴对称轴左侧y随x的增大而增大,
∵m<n<3,
∴y1<y2.
20.解:在直线y=2x﹣3上任取一点A(0,﹣3),由题意知A向右平移3个单位,再向上平移1个单位得到A′(3,﹣2),
设平移后的解析式为y=2x+b,
则A′(3,﹣2)在y=2x+b的解析式上,
﹣2=2×3+b,
解得:b=﹣8,
所以平移后的直线的解析式为y=2x﹣8.
21.解:(1)∵抛物线y=﹣x2+2x=﹣(x﹣1)2+1,
∴顶点坐标为(1,1),开口向下,过原点,画图如下:
(2)图象向上平移2单位,把各点的纵坐标加2,横坐标不变,画图如下:
(3)向上平移2个单位后的解析式为y=﹣x2+2x+2.
22.解:(1)把点C(5,4)代入抛物线y=ax2﹣5ax+4a,
得25a﹣25a+4a=4,
解得a=1.
∴该二次函数的解析式为y=x2﹣5x+4.
∵y=x2﹣5x+4=(x﹣)2﹣,
∴顶点坐标为P(,﹣).
(2)如先向左平移3个单位,再向上平移4个单位.
得到的二次函数解析式为y=(x﹣+3)2﹣+4=(x+)2+,
即y=x2+x+2.
一、选择题
1.如图是二次函数y=ax2+bx+c的图象,有下面四个结论:
①abc>0;②a﹣b+c>0;③2a+3b>0;④c﹣4b>0
其中,正确的结论是( )
A.①②
B.①②③
C.①②④
D.①③④
2.作抛物线A关于x轴对称的抛物线B,再将抛物线B向左平移2个单位,向上平移1个单位,得到的抛物线C的函数解析式是y=2(x+1)2﹣1,则抛物线A所对应的函数表达式是( )
A.y=﹣2(x+3)2﹣2
B.y=﹣2(x+3)2+2
C.y=﹣2(x﹣1)2﹣2
D.y=﹣2(x﹣1)2+2
3.方程x2+2x+1=的正数根的个数为( )
A.0
B.1
C.2
D.3
4.如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )
A.
B.
C.
D.
二、填空题
5.二次函数y=ax2+bx+c(a≠0)的函数值y与自变量x之间的部分对应值如下表:
x
…
﹣2
﹣1
0
1
2
…
y
…
﹣7
﹣1
3
5
5
…
则的值为
.
6.已知二次函数y=3(x﹣1)2+k的图象上三点A(2,y1),B(3,y2),C(﹣4,y3),则y1、y2、y3的大小关系是
.
7.已知二次函数y=ax2+bx+c中,自变量x与函数y的部分对应值如下表:
x
…
﹣2
0
2
3
…
y
…
8
0
0
3
…
当x=﹣1时,y=
.
8.若点A(2,m)在抛物线y=x2上,则点A关于原点对称点的坐标是
.
9.已知点A(a,m)、B(b,m)、P(a+b,n)为抛物线y=x2﹣2x﹣2上的点,则n=
.
10.把抛物线y=2x2先向下平移1个单位,再向左平移2个单位,得到的抛物线的解析式是
.
11.已知点A(4,y1),B(,y2),C(﹣2,y3)都在二次函数y=(x﹣2)2﹣m的图象上,则y1,y2,y3的大小关系为
.
12.如图所示,在同一平面直角坐标系中,作出①y=﹣3x2,②y=﹣,③y=﹣x2的图象,则从里到外的三条抛物线对应的函数依次是
(填序号)
13.将抛物线y=x2的图象向上平移1个单位,则平移后的抛物线的解析式为
.
14.将抛物线y=﹣x2向左平移2个单位后,得到的抛物线的解析式是
.
15.若抛物线y=2x2﹣px+4p+1中不管p取何值时都通过定点,则定点坐标为
.
16.已知抛物线y=x2﹣2x+5经过两点A(﹣2,y1)和B(3,y2),则y1与y2的大小关系是
.
17.a、b、c是实数,点A(a+1、b)、B(a+2,c)在二次函数y=x2﹣2ax+3的图象上,则b、c的大小关系是b
c(用“>”或“<”号填空)
三、解答题
18.已知抛物线y=ax2+bx﹣3(a≠0)经过点(﹣1,0),(3,0),求a,b的值.
19.已知抛物线y=a(x﹣3)2+2经过点(1,﹣2).
(1)求a的值;
(2)若点A(m,y1)、B(n,y2)(m<n<3)都在该抛物线上,试比较y1与y2的大小.
20.先阅读以下材料,然后解答问题:
材料:将二次函数y=﹣x2+2x+3的图象向左平移1个单位,再向下平移2个单位,求平移后的抛物线的解析式(平移后抛物线的形状不变).
解:在抛物线y=﹣x2+2x+3图象上任取两点A(0,3)、B(1,4),由题意知:点A向左平移1个单位得到A′(﹣1,3),再向下平移2个单位得到A″(﹣1,1);点B向左平移1个单位得到B′(0,4),再向下平移2个单位得到B″(0,2).
设平移后的抛物线的解析式为y=﹣x2+bx+c.则点A″(﹣1,1),B″(0,2)在抛物线上.可得:,解得:.所以平移后的抛物线的解析式为:y=﹣x2+2.
根据以上信息解答下列问题:
将直线y=2x﹣3向右平移3个单位,再向上平移1个单位,求平移后的直线的解析式.
21.(1)请在坐标系中画出二次函数y=﹣x2+2x的大致图象;
(2)在同一个坐标系中画出y=﹣x2+2x的图象向上平移两个单位后的图象;
(3)直接写出平移后的图象的解析式.
注:图中小正方形网格的边长为1.
22.如图抛物线y=ax2﹣5ax+4a与x轴相交于点A、B,且过点C(5,4).
(1)求a的值和该抛物线顶点P的坐标.
(2)请你设计一种平移的方法,使平移后抛物线的顶点落在第二象限,并写出平移后抛物线的解析式.
参考答案
1.解:∵抛物线开口向上,
∴a>0;
∵抛物线的对称轴在y轴的右侧,
∴x=﹣>0,
∴b<0;
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc>0,所以①正确;
∵x=﹣1时,y>0,
∴a﹣b+c>0,所以②正确;
∵x=﹣=,
∴2a+3b=0,所以③错误;
∵x=2时,y>0,
∴4a+2b+c>0,
把2a=﹣3b代入得﹣6b+2b+c>0,
∴c﹣4b>0,所以④正确.
故选:C.
2.解:易得抛物线C的顶点为(﹣1,﹣1),
∵是向左平移2个单位,向上平移1个单位得到抛物线C的,
∴抛物线B的坐标为(1,﹣2),
可设抛物线B的坐标为y=2(x﹣h)2+k,代入得:y=2(x﹣1)2﹣2,
易得抛物线A的二次项系数为﹣2,顶点坐标为(1,2),
∴抛物线A的解析式为y=﹣2(x﹣1)2+2.
故选:D.
3.解:二次函数y=x2+2x+1=(x+1)2的图象过点(0,1),且在第一、二象限内,
反比例函数y=的图象在第一、三象限,
∴这两个函数只在第一象限有一个交点.
即方程x2+2x+1=的正数根的个数为1.
故选:B.
4.解:∵a<0,
∴抛物线的开口方向向下,
故第三个选项错误;
∵c<0,
∴抛物线与y轴的交点为在y轴的负半轴上,
故第一个选项错误;
∵a<0、b>0,对称轴为x=>0,
∴对称轴在y轴右侧,
故第四个选项错误.
故选:B.
5.解:∵x=1、x=2时的函数值都是﹣1相等,
∴此函数图象的对称轴为直线x=﹣==,
即=﹣.
故答案为:﹣.
6.解:∵y=3(x﹣1)2+k,
∴图象的开口向上,对称轴是直线x=1,
A(﹣4,y3)关于直线x=1的对称点是(6,y3),
∵2<3<6,
∴y1<y2<y3,
故答案为y1<y2<y3.
7.解:依据表格可知抛物线的对称轴为x=1,
∴当x=﹣1时与x=3时函数值相同,
∴当x=﹣1时,y=3.
故答案为:3.
8.解:∵点A(2,m)在抛物线y=x2上,
∴m=4,
∴A(2,4),
∴点A关于原点对称点的坐标是(﹣2,﹣4),
故答案为:(﹣2,﹣4).
9.解:∵抛物线解析式为y=x2﹣2x﹣2=(x﹣1)2﹣3,
∴该抛物线的对称轴是直线x=1,
又∵点A(a,m)和B(b,m)关于直线x=1对称,
∴=1,
∴a+b=2,
把(2,n)代入抛物线的解析式得,n=22﹣2×2﹣2=﹣2.
故答案是:﹣2.
10.解:由“上加下减”的原则可知,二次函数y=2x2的图象向下平移1个单位得到y=2x2﹣1,
由“左加右减”的原则可知,将二次函数y=2x2﹣1的图象向左平移2个单位可得到函数y=2(x+2)2﹣1,
故答案是:y=2(x+2)2﹣1.
11.解:A(4,y1),B(,y2),在对称轴的右侧,y随x的增大而增大,
∵<4,
∴y2<y1,
∴点A离直线x=2近,点C离直线x=2最远,
而抛物线开口向上,
则y3>y1,
故y3>y1>y2,
故答案是:y3>y1>y2.
12.解:①y=﹣3x2,
②y=﹣x2,
③y=﹣x2中,二次项系数a分别为﹣3、﹣、﹣1,
∵|﹣3|>|﹣1|>|﹣|,
∴抛物线②y=﹣x2的开口最宽,抛物线①y=﹣3x2的开口最窄.
故答案为:①③②.
13.解:∵抛物线y=x2的图象向上平移1个单位,
∴平移后的抛物线的解析式为y=x2+1.
故答案为:y=x2+1.
14.解:由“左加右减”的原则可知,抛物线y=﹣x2向左平移2个单位后,得到的抛物线的解析式是y=﹣(x+2)2,即y=﹣x2﹣4x﹣4.
故答案为:y=﹣x2﹣4x﹣4.
15.解:y=2x2﹣px+4p+1可化为y=2x2﹣p(x﹣4)+1,
分析可得:当x=4时,y=33;且与p的取值无关;
故不管p取何值时都通过定点(4,33).
16.解:∵抛物线y=x2﹣2x+5经过两点A(﹣2,y1)和B(3,y2),
∴y1=4+4+5=13,即y1=13,
y2=9﹣6+5=8,即y2=8,
∵8<13,
∴y2<y1.
故答案是:y1>y2.
17.解:∵二次函数y=x2﹣2ax+3的图象的对称轴为x=a,二次项系数1>0,
∴抛物线的开口向上,在对称轴的右边,y随x的增大而增大,
∵a+1<a+2,点A(a+1、b)、B(a+2,c)在二次函数y=x2﹣2ax+3的图象上,
∴b<c,
故答案为:<.
18.解:∵抛物线y=ax2+bx﹣3(a≠0)经过点(﹣1,0),(3,0),
∴,
解得,
,
即a的值是1,b的值是﹣2.
19.解:(1)∵抛物线y=a(x﹣3)2+2经过点(1,﹣2),
∴﹣2=a(1﹣3)2+2,
解得a=﹣1;
(2)∵函数y=﹣(x﹣3)2+2的对称轴为x=3,
∴A(m,y1)、B(n,y2)(m<n<3)在对称轴左侧,
又∵抛物线开口向下,
∴对称轴左侧y随x的增大而增大,
∵m<n<3,
∴y1<y2.
20.解:在直线y=2x﹣3上任取一点A(0,﹣3),由题意知A向右平移3个单位,再向上平移1个单位得到A′(3,﹣2),
设平移后的解析式为y=2x+b,
则A′(3,﹣2)在y=2x+b的解析式上,
﹣2=2×3+b,
解得:b=﹣8,
所以平移后的直线的解析式为y=2x﹣8.
21.解:(1)∵抛物线y=﹣x2+2x=﹣(x﹣1)2+1,
∴顶点坐标为(1,1),开口向下,过原点,画图如下:
(2)图象向上平移2单位,把各点的纵坐标加2,横坐标不变,画图如下:
(3)向上平移2个单位后的解析式为y=﹣x2+2x+2.
22.解:(1)把点C(5,4)代入抛物线y=ax2﹣5ax+4a,
得25a﹣25a+4a=4,
解得a=1.
∴该二次函数的解析式为y=x2﹣5x+4.
∵y=x2﹣5x+4=(x﹣)2﹣,
∴顶点坐标为P(,﹣).
(2)如先向左平移3个单位,再向上平移4个单位.
得到的二次函数解析式为y=(x﹣+3)2﹣+4=(x+)2+,
即y=x2+x+2.
同课章节目录
