1.3二次函数的性质 同步优生辅导训练 2021-2022学年浙教版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 1.3二次函数的性质 同步优生辅导训练 2021-2022学年浙教版九年级数学上册(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 279.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 00:00:00 | ||
图片预览




文档简介
2021-2022学年浙教版九年级数学上册《1.3二次函数的性质》同步优生辅导训练(附答案)
一、选择题
1.已知函数y=,则使y=k成立的x值恰好有三个,则k的值为( )
A.0
B.1
C.2
D.3
2.给出下列函数:①y=2x;②y=﹣2x+1;③y=(x>0);④y=x2(x<﹣1).其中,y随x的增大而减小的函数是( )
A.①②
B.①③
C.②④
D.②③④
3.将y=(2x﹣1)?(x+2)+1化成y=a(x+m)2+n的形式为( )
A.
B.
C.
D.
4.二次函数y=x2﹣x+m(m为常数)的图象如图所示,当x=a时,y<0;那么当x=a﹣1时,函数值( )
A.y<0
B.0<y<m
C.y>m
D.y=m
5.二次函数y=﹣x2+6x﹣7,当x取值为t≤x≤t+2时,y最大值=﹣(t﹣3)2+2,则t的取值范围是( )
A.t=0
B.0≤t≤3
C.t≥3
D.以上都不对
6.若实数x,y满足条件2x2﹣6x+y2=0,则x2+y2+2x的最大值是( )
A.14
B.15
C.16
D.不能确定
7.已知一条抛物线经过E(0,10),F(2,2),G(4,2),H(3,1)四点,选择其中两点用待定系数法能求出抛物线解析式的为( )
A.E,F
B.E,G
C.E,H
D.F,G
8.下面说法错误的是( )
A.直线y=x就是一、三象限的角平分线
B.函数y=3x﹣10的图象经过点(3,﹣1)C.函数中y随x的增大而减小
D.抛物线y=x2﹣2x+1的对称轴是直线x=1
9.已知:二次函数y=x2+2x+a(a为大于0的常数),当x=m时的函数值y1<0;则当x=m+2时的函数值y2与0的大小关系为( )
A.y2>0
B.y2<0
C.y2=O
D.不能确定
10.下列函数:①y=2x﹣3,②y=﹣6x,③,④,⑤y=4x2+2x,其中y随着x的增大而减小有( )
A.1个
B.2个
C.3个
D.4个
11.在初中已学过的一次函数、反比例函数和二次函数等函数中,它们的图象与任意一条直线x=a(a是任意实数)交点的个数为( )
A.必有一个
B.一个或两个
C.至少一个
D.至多一个
12.若二次函数y=ax2+bx+1的图象与平行于x轴的直线交于二点的横坐标分别为m、n.则:当x=m+n时,二次函数y的值是( )
A.1
B.2
C.﹣1
D.O
二、填空题
13.已知抛物线y=x2,过其对称轴上一点P的直线AB交抛物线于A,B两点,且∠AOB=Rt∠,试写出满足条件的直线AB的解析式
(只要写出一个即可)
14.已知M、N两点关于y轴对称,且点M在双曲线上,点N在直线y=﹣x+3上,设点M坐标为(a,b),则y=﹣abx2+(a+b)x的顶点坐标为
.
15.若的最大值为a,最小值为b,则a2+b2的值为
.
16.若直线y=b(b为实数)与函数y=|x2﹣4x+3|的图象至少有三个公共点,则实数b的取值范围是
.
17.已知函数y=4x2﹣4ax+a2﹣2a+2在0≤x≤2上有最小值3,则a的值
.
18.若二次函数y=x2+(a+17)x+38﹣a与反比例函数y=的交点是整点(横坐标和纵坐标都是整数的点),则正整数a的值是
.
19.老师给出一个函数,甲,乙,丙,丁四位同学各指出这个函数的一个性质:
甲:函数的图象不经过第三象限;乙:函数的图象经过第一象限;
丙:当x<2时,y随x的增大而减小;丁:当x<2时,y>0.
已知这四位同学叙述都正确,请构造出满足上述所有性质的一个函数
.
20.已知函数y=x2+2ax+a2﹣1在0≤x≤3范围内有最大值24最小值3,则实数a的值为
.
21.分式的最小值是
.
22.如果抛物线y=x2﹣6x+c﹣2的顶点到x轴的距离是3,那么c的值等于
.
23.设a,b满足a2+b2﹣2a﹣4=0,则2a﹣b的最大值与最小值之差为
.
24.设x、y、z满足关系式x﹣1==,则x2+y2+z2的最小值为
.
三、解答题
25.已知抛物线y=﹣x2+bx+c与直线y=﹣x+m相交于第一象限内不同的两点A(4,n),B(1,4),
(1)求此抛物线的解析式.
(2)抛物线上是否存在点P,使直线OP将线段AB平分?若存在直接求出P点坐标;若不存在说明理由.
26.如图所示,抛物线y=ax2+bx+c经过A(﹣2,0)、B(4,0)、C(0,4)三点,抛物线对称轴与x轴交于点D.
(1)求该抛物线的解析式;
(2)若点E为对称轴上一点,将线段ED绕点E顺时针方向旋转90°得到线段EF,若点F恰好在该抛物线上,求线段DE的长.
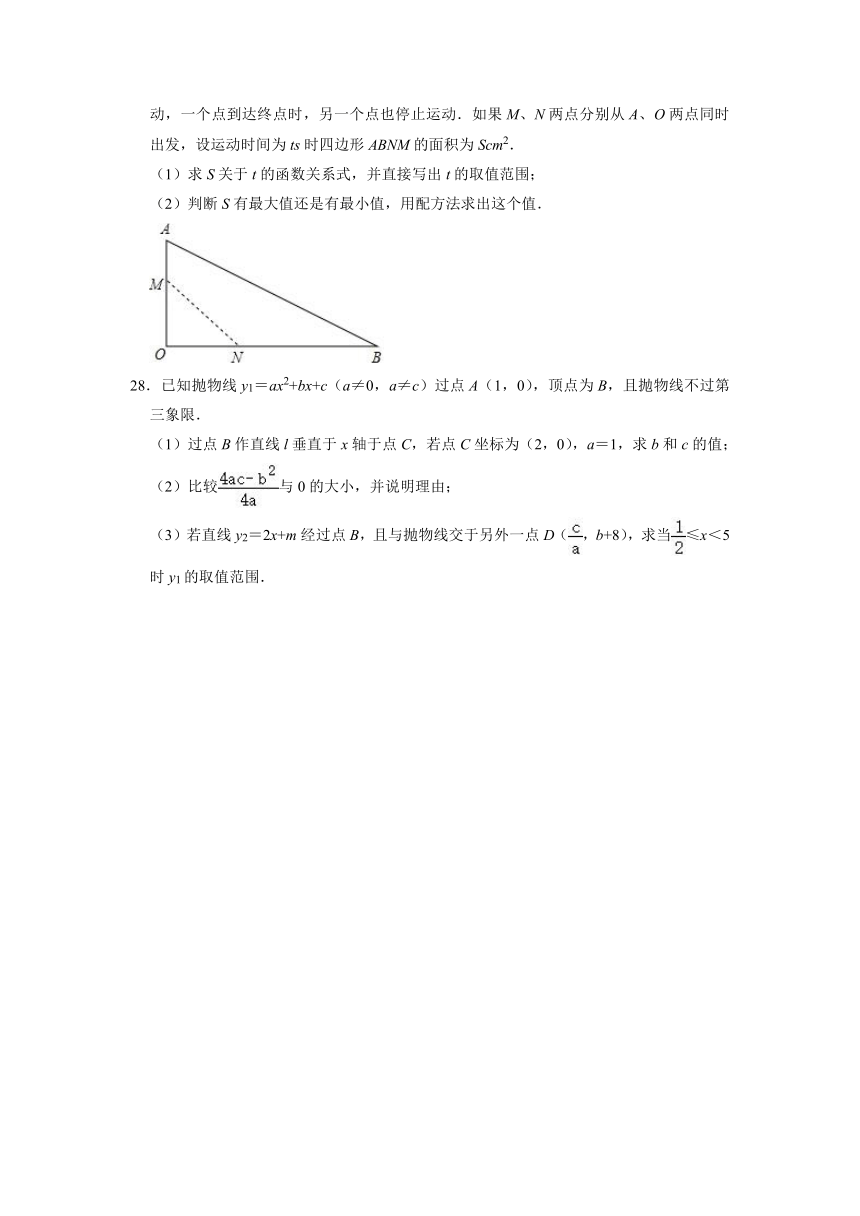
27.如图,在△AOB中,∠O=90°,AO=18cm,BO=30cm,动点M从点A开始沿边AO以1cm/s的速度向终点O移动,动点N从点O开始沿边OB以2cm/s的速度向终点B移动,一个点到达终点时,另一个点也停止运动.如果M、N两点分别从A、O两点同时出发,设运动时间为ts时四边形ABNM的面积为Scm2.
(1)求S关于t的函数关系式,并直接写出t的取值范围;
(2)判断S有最大值还是有最小值,用配方法求出这个值.
28.已知抛物线y1=ax2+bx+c(a≠0,a≠c)过点A(1,0),顶点为B,且抛物线不过第三象限.
(1)过点B作直线l垂直于x轴于点C,若点C坐标为(2,0),a=1,求b和c的值;
(2)比较与0的大小,并说明理由;
(3)若直线y2=2x+m经过点B,且与抛物线交于另外一点D(,b+8),求当≤x<5时y1的取值范围.
参考答案
1.解:如图,
当y=k成立的x值恰好有三个,即直线y=k与两抛物线有三个交点,
而当x=3,两函数的函数值都为3,即它们的交点为(3,3),
所以k=3.
故选:D.
2.解:①y=2x,正比例函数,k>0,故y随着x的增大而增大;
②y=﹣2x+1,一次函数,k<0,故y随着x增大而减小;
③y=(x>0),反比例函数,k>0在第一象限内y随x的增大而减小;
④y=x2(x<﹣1),图象在对称轴右侧,y随着x的增大而增大;而在对称轴左侧,y随着x的增大而减小.
故选:D.
3.解:y=(2x﹣1)(x+2)+1
=2x2+3x﹣1
=2(x2+x+)﹣﹣1
=2(x+)2﹣.
故选:C.
4.解:∵对称轴是直线x=,0<x1<
故由对称性<x2<1
当x=a时,y<0,
则a的范围是x1<a<x2,
所以a﹣1<0,
当x时y随x的增大而减小,
当x=0时函数值是m.
因而当x=a﹣1<0时,函数值y一定大于m.
故选:C.
5.解:∵y=﹣x2+6x﹣7=﹣(x﹣3)2+2,
当t≤3≤t+2时,即1≤t≤3时,函数为增函数,
ymax=f(3)=2,与ymax=﹣(t﹣3)2+2矛盾.
当3≥t+2时,即t≤1时,ymax=f(t+2)=﹣(t﹣1)2+2,与ymax=﹣(t﹣3)2+2矛盾.
当3≤t,即t≥3时,ymax=f(t)=﹣(t﹣3)2+2与题设相等,
故t的取值范围t≥3,
故选:C.
6.解:由已知得:y2=﹣2x2+6x,
∴x2+y2+2x=x2﹣2x2+6x+2x,
=﹣x2+8x,
=﹣(x﹣4)2+16,
又y2=﹣2x2+6x≥0,
解得:0≤x≤3,
∴当x=3时,y=0,所以x2+y2+2x的最大值为15.
故选:B.
7.解:∵F(2,2),G(4,2),
∴F和G点为抛物线上的对称点,
∴抛物线的对称轴为直线x=3,
∴H(3,1)点为抛物线的顶点,
设抛物线的解析式为y=a(x﹣3)2+1,
把E(0,10)代入得9a+1=10,解得a=1,
∴抛物线的解析式为y=(x﹣3)2+1.
故选:C.
8.解:A、直线y=x就是一、三象限的角平分线,正确,
B、把点(3,﹣1)代入y=3x﹣10中,式子成立,正确,
C、反比例函数系数k=2,函数图象经过一三象限,在各个象限内,y随x增大而减小,在整个定义域内y不是随x增大而减小,故本选项错误,
D、抛物线y=x2﹣2x+1=(x﹣1)2,故可得对称轴为x=1,正确.
故选:C.
9.解:设二次函数y=x2+2x+a的图象与x轴交于点(x1,0)、(x2,0)(x1<x2),
∵当x=0时,y=x2+2x+a=a≥0,且抛物线的对称轴为直线x=﹣=﹣1,
∴﹣2≤x1<m<x2≤0,
∴0<m+2<2,
∴当x=m+2时,函数值y>0.
故选:A.
10.解:①因为k>0,可知函数随x的增大而增大,此选项错误;
②由于k<0,可知函数随x的增大而减小,此选项正确;
③是反比例函数,有两个象限,此选项错误;
④是反比例函数,有两个象限,此选项错误;
⑤函数是二次函数,故以对称轴为分界线,两边既有增大而减小的,也有增大而增大的,此选项错误.
故选:A.
11.解:∵任意一条直线x=a(a是任意实数)是平行于y轴的一条直线,
∴在初中已学过的一次函数、反比例函数和二次函数等函数中,
只有反比例函数与x=0时,没有交点,其他只有一个交点.
∴它们的图象与任意一条直线x=a交点的个数至多有一个.
故选:D.
12.解:∵过横坐标分别为m、n的两点的直线与x轴平行,
∴m+n=﹣×2,
∴=﹣,
∴=﹣,
即x=m+n与x=0关于对称轴对称,
∴x=m+n时,二次函数y的函数值与x=0时的函数值相等,
当x=0时,y=a×02+b×0+1=1,
∴当x=m+n时,二次函数y的值是1.
故选:A.
13.解:设A(x1,x12)、B(x2,x22),
∵∠AOB=Rt∠,
∴OA2+OB2=AB2,
即x12+x14+x2+x24=(x1﹣x2)2+(x12﹣x22)2,
整理可得x1x2=﹣4,
设直线AB解析式为y=kx+b,
则,
两式相减可得k=(x1+x2),
,b=2,
取k=1,
∴y=x+2,
故答案为:y=x+2
14.解:∵M、N两点关于y轴对称,
∴M坐标为(a,b),N为(﹣a,b),分别代入相应的函数中得,b=①,a+3=b②,
∴ab=,(a+b)2=(a﹣b)2+4ab=11,a+b=±,
∴y=﹣x2±x,
∵=±,=,
∴顶点坐标(,)或(﹣,).
故答案为:(,)或(﹣,).
15.解:由1﹣x≥0,且≥0,得≤x≤1.
.
由于,
所以当时,y2取到最大值1,故a=1.
当或1时,y2取到最小值,故.
所以:.
故答案为:.
16.解:∵当x2﹣4x+3=0时,x=1或x=3,
∴当x<1或x>3时,x2﹣4x+3>0,即:y=|x2﹣4x+3|,函数值大于0,
当1<x<3时,﹣1≤x2﹣4x+3<0,即:y=|﹣x2+4x﹣3|,函数最大值为1,
故符合条件的实数b的取值范围是0<b≤1.
17.解:配方得y=4(x﹣)2﹣2a+2,故函数图象开口朝上,且对称轴为x=.
当≤0,即a≤0时,当x=0时,y最小值=a2﹣2a+2=3,解得a=1﹣或a=1+(舍);
当0<<2,即0<a<4时,当x=时,y最小值=﹣2a+2=3,解得a=﹣(舍);
当≥2时,当x=2时,y最小值=8﹣8a+a2﹣2a+2=3,
解得a=5+.
综上所述,a的值是1﹣或5+.
故答案是:1﹣或5+.
18.解:联立方程组
,
消去y得,x2+(a+17)x+38﹣a=,
即x3+(a+17)x2+(38﹣a)x﹣56=0,
当x=1时,x3+(a+17)x2+(38﹣a)x﹣56=0,
∴式子x3+(a+17)x2+(38﹣a)x﹣56中含有因式(x﹣1),
分解因式得(x﹣1)[x2+(a+18)x+56]=0,(1)
显然x1=1是方程(1)的一个根,(1,56)是两个函数的图象的一个交点.
因为a是正整数,所以关于x的方程x2+(a+18)x+56=0,(2)
其判别式Δ=(a+18)2﹣224>0,它一定有两个不同的实数根.
而两个函数的图象的交点都是整点,所以方程(2)的根都是整数,
因此它的判别式Δ=(a+18)2﹣224应该是一个完全平方数.
设(a+18)2﹣224=k2(其中k为非负整数),则(a+18)2﹣k2=224,即(a+18+k)(a+18﹣k)=224.
显然a+18+k与a+18﹣k的奇偶性相同,且a+18+k≥18,而224=112×2=56×4=28×8,
所以
或或,
解得
或
或.
而a是正整数,所以只可能
或.
故答案为:a=39或a=12.
19.解:∵当x<2时,y随x的增大而减小.当x<2时,y>0.
∴可以写一个对称轴是直线x=2,开口向上的二次函数就可以.
∵函数的图象不经过第三象限.
∴所写的二次函数的顶点可以在x轴上方,
设顶点是(2,0),并且二次项系数大于0的二次函数,就满足条件.
如y=(x﹣2)2,答案不唯一.
故答案为:y=(x﹣2)2.
20.解:配方y=(x+a)2﹣1,
函数的对称轴为直线x=﹣a,
顶点坐标为(﹣a,﹣1).
①当0≤﹣a≤3即﹣3≤a≤0时,
函数最小值为﹣1,不合题意;
②当﹣a<0即a>0时,
∵当x=3时,y有最大值;当x=0时,y有最小值,
∴,解得a=2;
③当﹣a>3即a<﹣3时,
∵当x=3时,y有最小值;当x=0时,y有最大值,
∴,解得a=﹣5.
∴实数a的值为2或﹣5.
故答案为2或﹣5.
21.解:令y==6﹣,
问题转化为考虑函数z=x2+2x+2的最小值,
∵z=x2+2x+2=(x+1)2+1
∴当x=﹣1时,zmin=1,
∴ymin=6﹣2=4,
即分式分式的最小值是:4.
故答案为:4.
22.解:由题意,得:=±3,
当=3时,c=14,
当=﹣3时,c=8.
即c的值为14或8.
故答案为:14或8.
23.解:设t=2a﹣b,故b=2a﹣t,
∵a2+b2﹣2a﹣4=0,
∴a2+4a2﹣4at+t2﹣2a﹣4=0,
即5a2﹣(4t+2)a+t2﹣4=0,
Δ=(4t+2)2﹣20(t2﹣4)≥0,
解得﹣3≤t≤7,
故2a﹣b的最大值与最小值之差为7﹣(﹣3)=10.
故答案为10.
24.解:令x﹣1===k,则x=k+1,y=2k﹣1,z=3k+2,
于是x2+y2+z2=(k+1)2+(2k﹣1)2+(3k+2)2,
=k2+2k+1+4k2+1﹣4k+9k2+4+12k
=14k2+10k+6,
其最小值为==.
25.解:(1)把B(1,4)代入y=﹣x+m得,m=5,
∴直线的解析式为:y=﹣x+5,
∴A(4,1),
把A(4,1),B(1,4)代入y=﹣x2+bx+c得,,
解得:,
∴抛物线解析式为:y=﹣x2+4x+1;
(2)存在,
设P点坐标为(m,﹣m2+4m+1),
∵线段AB的中点E的坐标为(,),
∴直线OP的解析式为:y=x,
∴m=﹣m2+4m+1,
解得:m=或m=,
∴P点坐标为(,)(,).
26.解:(1)把A(﹣2,0)、B(4,0)、C(0,4)代入y=ax2+bx+c得,,
解得:,
∴该抛物线的解析式为:y=﹣x2+x+4;
(2)∵x=﹣=1,
∴D(1,0),
∵点E为对称轴上一点,
∴设E(1,m),
则DE=|m|,
∵将线段ED绕点E顺时针方向旋转90°得到线段EF,
∴∠FED=90°,EF=DE=|m|,
当点E在x轴的上面,
∴F(1﹣m,m),
∵点F恰好在该抛物线上,
∴m=﹣(1﹣m)2+(1﹣m)+4,
解得:m=﹣1+,m=﹣1﹣,(不合题意,舍去),
当点E在x轴的下面,
∴F(1﹣m,m),
∵点F恰好在该抛物线上,
∴m=﹣(1﹣m)2+1﹣m+4,
解得:m=﹣1+(舍弃),m=﹣1﹣,
∴线段DE的长为:﹣1或1+.
27.解:(1)由题意得,AM=t,ON=2t,则OM=OA﹣AM=18﹣t,
四边形ABNM的面积S=△AOB的面积﹣△MON的面积
=×18×30﹣×(18﹣t)×2t
=t2﹣18t+270(0<t≤15);
(2)S=t2﹣18t+270
=t2﹣18t+81﹣81+270
=(t﹣9)2+189,
∵a=1>0,
∴S有最小值,这个值是189.
28.解:∵抛物线y1=ax2+bx+c(a≠0,a≠c),经过A(1,0),
抛物线不过第三象限,则a>0,
把点代入函数即可得到:b=﹣a﹣c;
(1)由题意得:函数对称轴是直线x=2=,而a=1、b=﹣a﹣c,
解得:b=﹣4,c=3;
(2)由抛物线开口向上,且过点A,知:顶点在x轴下方,
即:<0;
(3)由韦达定理得:
x1+x2=,x1x2=,
其中x1=1,则x2=,而D坐标是(,b+8),
故:b+8=0,即b=﹣8,
∵a+c=﹣b,∴a+c=8…①,
把B、C两点代入直线解析式易得:c﹣a=4…②,
联立①、②并求解得:a=2,c=6
函数表达式为:y=2x2﹣8x+6,
A、B、C点的坐标分别为(1,0)、(2,﹣2)、(3,0)
当≤x<5时,
y1的取值范围易证为:16>y1≥﹣2,
一、选择题
1.已知函数y=,则使y=k成立的x值恰好有三个,则k的值为( )
A.0
B.1
C.2
D.3
2.给出下列函数:①y=2x;②y=﹣2x+1;③y=(x>0);④y=x2(x<﹣1).其中,y随x的增大而减小的函数是( )
A.①②
B.①③
C.②④
D.②③④
3.将y=(2x﹣1)?(x+2)+1化成y=a(x+m)2+n的形式为( )
A.
B.
C.
D.
4.二次函数y=x2﹣x+m(m为常数)的图象如图所示,当x=a时,y<0;那么当x=a﹣1时,函数值( )
A.y<0
B.0<y<m
C.y>m
D.y=m
5.二次函数y=﹣x2+6x﹣7,当x取值为t≤x≤t+2时,y最大值=﹣(t﹣3)2+2,则t的取值范围是( )
A.t=0
B.0≤t≤3
C.t≥3
D.以上都不对
6.若实数x,y满足条件2x2﹣6x+y2=0,则x2+y2+2x的最大值是( )
A.14
B.15
C.16
D.不能确定
7.已知一条抛物线经过E(0,10),F(2,2),G(4,2),H(3,1)四点,选择其中两点用待定系数法能求出抛物线解析式的为( )
A.E,F
B.E,G
C.E,H
D.F,G
8.下面说法错误的是( )
A.直线y=x就是一、三象限的角平分线
B.函数y=3x﹣10的图象经过点(3,﹣1)C.函数中y随x的增大而减小
D.抛物线y=x2﹣2x+1的对称轴是直线x=1
9.已知:二次函数y=x2+2x+a(a为大于0的常数),当x=m时的函数值y1<0;则当x=m+2时的函数值y2与0的大小关系为( )
A.y2>0
B.y2<0
C.y2=O
D.不能确定
10.下列函数:①y=2x﹣3,②y=﹣6x,③,④,⑤y=4x2+2x,其中y随着x的增大而减小有( )
A.1个
B.2个
C.3个
D.4个
11.在初中已学过的一次函数、反比例函数和二次函数等函数中,它们的图象与任意一条直线x=a(a是任意实数)交点的个数为( )
A.必有一个
B.一个或两个
C.至少一个
D.至多一个
12.若二次函数y=ax2+bx+1的图象与平行于x轴的直线交于二点的横坐标分别为m、n.则:当x=m+n时,二次函数y的值是( )
A.1
B.2
C.﹣1
D.O
二、填空题
13.已知抛物线y=x2,过其对称轴上一点P的直线AB交抛物线于A,B两点,且∠AOB=Rt∠,试写出满足条件的直线AB的解析式
(只要写出一个即可)
14.已知M、N两点关于y轴对称,且点M在双曲线上,点N在直线y=﹣x+3上,设点M坐标为(a,b),则y=﹣abx2+(a+b)x的顶点坐标为
.
15.若的最大值为a,最小值为b,则a2+b2的值为
.
16.若直线y=b(b为实数)与函数y=|x2﹣4x+3|的图象至少有三个公共点,则实数b的取值范围是
.
17.已知函数y=4x2﹣4ax+a2﹣2a+2在0≤x≤2上有最小值3,则a的值
.
18.若二次函数y=x2+(a+17)x+38﹣a与反比例函数y=的交点是整点(横坐标和纵坐标都是整数的点),则正整数a的值是
.
19.老师给出一个函数,甲,乙,丙,丁四位同学各指出这个函数的一个性质:
甲:函数的图象不经过第三象限;乙:函数的图象经过第一象限;
丙:当x<2时,y随x的增大而减小;丁:当x<2时,y>0.
已知这四位同学叙述都正确,请构造出满足上述所有性质的一个函数
.
20.已知函数y=x2+2ax+a2﹣1在0≤x≤3范围内有最大值24最小值3,则实数a的值为
.
21.分式的最小值是
.
22.如果抛物线y=x2﹣6x+c﹣2的顶点到x轴的距离是3,那么c的值等于
.
23.设a,b满足a2+b2﹣2a﹣4=0,则2a﹣b的最大值与最小值之差为
.
24.设x、y、z满足关系式x﹣1==,则x2+y2+z2的最小值为
.
三、解答题
25.已知抛物线y=﹣x2+bx+c与直线y=﹣x+m相交于第一象限内不同的两点A(4,n),B(1,4),
(1)求此抛物线的解析式.
(2)抛物线上是否存在点P,使直线OP将线段AB平分?若存在直接求出P点坐标;若不存在说明理由.
26.如图所示,抛物线y=ax2+bx+c经过A(﹣2,0)、B(4,0)、C(0,4)三点,抛物线对称轴与x轴交于点D.
(1)求该抛物线的解析式;
(2)若点E为对称轴上一点,将线段ED绕点E顺时针方向旋转90°得到线段EF,若点F恰好在该抛物线上,求线段DE的长.
27.如图,在△AOB中,∠O=90°,AO=18cm,BO=30cm,动点M从点A开始沿边AO以1cm/s的速度向终点O移动,动点N从点O开始沿边OB以2cm/s的速度向终点B移动,一个点到达终点时,另一个点也停止运动.如果M、N两点分别从A、O两点同时出发,设运动时间为ts时四边形ABNM的面积为Scm2.
(1)求S关于t的函数关系式,并直接写出t的取值范围;
(2)判断S有最大值还是有最小值,用配方法求出这个值.
28.已知抛物线y1=ax2+bx+c(a≠0,a≠c)过点A(1,0),顶点为B,且抛物线不过第三象限.
(1)过点B作直线l垂直于x轴于点C,若点C坐标为(2,0),a=1,求b和c的值;
(2)比较与0的大小,并说明理由;
(3)若直线y2=2x+m经过点B,且与抛物线交于另外一点D(,b+8),求当≤x<5时y1的取值范围.
参考答案
1.解:如图,
当y=k成立的x值恰好有三个,即直线y=k与两抛物线有三个交点,
而当x=3,两函数的函数值都为3,即它们的交点为(3,3),
所以k=3.
故选:D.
2.解:①y=2x,正比例函数,k>0,故y随着x的增大而增大;
②y=﹣2x+1,一次函数,k<0,故y随着x增大而减小;
③y=(x>0),反比例函数,k>0在第一象限内y随x的增大而减小;
④y=x2(x<﹣1),图象在对称轴右侧,y随着x的增大而增大;而在对称轴左侧,y随着x的增大而减小.
故选:D.
3.解:y=(2x﹣1)(x+2)+1
=2x2+3x﹣1
=2(x2+x+)﹣﹣1
=2(x+)2﹣.
故选:C.
4.解:∵对称轴是直线x=,0<x1<
故由对称性<x2<1
当x=a时,y<0,
则a的范围是x1<a<x2,
所以a﹣1<0,
当x时y随x的增大而减小,
当x=0时函数值是m.
因而当x=a﹣1<0时,函数值y一定大于m.
故选:C.
5.解:∵y=﹣x2+6x﹣7=﹣(x﹣3)2+2,
当t≤3≤t+2时,即1≤t≤3时,函数为增函数,
ymax=f(3)=2,与ymax=﹣(t﹣3)2+2矛盾.
当3≥t+2时,即t≤1时,ymax=f(t+2)=﹣(t﹣1)2+2,与ymax=﹣(t﹣3)2+2矛盾.
当3≤t,即t≥3时,ymax=f(t)=﹣(t﹣3)2+2与题设相等,
故t的取值范围t≥3,
故选:C.
6.解:由已知得:y2=﹣2x2+6x,
∴x2+y2+2x=x2﹣2x2+6x+2x,
=﹣x2+8x,
=﹣(x﹣4)2+16,
又y2=﹣2x2+6x≥0,
解得:0≤x≤3,
∴当x=3时,y=0,所以x2+y2+2x的最大值为15.
故选:B.
7.解:∵F(2,2),G(4,2),
∴F和G点为抛物线上的对称点,
∴抛物线的对称轴为直线x=3,
∴H(3,1)点为抛物线的顶点,
设抛物线的解析式为y=a(x﹣3)2+1,
把E(0,10)代入得9a+1=10,解得a=1,
∴抛物线的解析式为y=(x﹣3)2+1.
故选:C.
8.解:A、直线y=x就是一、三象限的角平分线,正确,
B、把点(3,﹣1)代入y=3x﹣10中,式子成立,正确,
C、反比例函数系数k=2,函数图象经过一三象限,在各个象限内,y随x增大而减小,在整个定义域内y不是随x增大而减小,故本选项错误,
D、抛物线y=x2﹣2x+1=(x﹣1)2,故可得对称轴为x=1,正确.
故选:C.
9.解:设二次函数y=x2+2x+a的图象与x轴交于点(x1,0)、(x2,0)(x1<x2),
∵当x=0时,y=x2+2x+a=a≥0,且抛物线的对称轴为直线x=﹣=﹣1,
∴﹣2≤x1<m<x2≤0,
∴0<m+2<2,
∴当x=m+2时,函数值y>0.
故选:A.
10.解:①因为k>0,可知函数随x的增大而增大,此选项错误;
②由于k<0,可知函数随x的增大而减小,此选项正确;
③是反比例函数,有两个象限,此选项错误;
④是反比例函数,有两个象限,此选项错误;
⑤函数是二次函数,故以对称轴为分界线,两边既有增大而减小的,也有增大而增大的,此选项错误.
故选:A.
11.解:∵任意一条直线x=a(a是任意实数)是平行于y轴的一条直线,
∴在初中已学过的一次函数、反比例函数和二次函数等函数中,
只有反比例函数与x=0时,没有交点,其他只有一个交点.
∴它们的图象与任意一条直线x=a交点的个数至多有一个.
故选:D.
12.解:∵过横坐标分别为m、n的两点的直线与x轴平行,
∴m+n=﹣×2,
∴=﹣,
∴=﹣,
即x=m+n与x=0关于对称轴对称,
∴x=m+n时,二次函数y的函数值与x=0时的函数值相等,
当x=0时,y=a×02+b×0+1=1,
∴当x=m+n时,二次函数y的值是1.
故选:A.
13.解:设A(x1,x12)、B(x2,x22),
∵∠AOB=Rt∠,
∴OA2+OB2=AB2,
即x12+x14+x2+x24=(x1﹣x2)2+(x12﹣x22)2,
整理可得x1x2=﹣4,
设直线AB解析式为y=kx+b,
则,
两式相减可得k=(x1+x2),
,b=2,
取k=1,
∴y=x+2,
故答案为:y=x+2
14.解:∵M、N两点关于y轴对称,
∴M坐标为(a,b),N为(﹣a,b),分别代入相应的函数中得,b=①,a+3=b②,
∴ab=,(a+b)2=(a﹣b)2+4ab=11,a+b=±,
∴y=﹣x2±x,
∵=±,=,
∴顶点坐标(,)或(﹣,).
故答案为:(,)或(﹣,).
15.解:由1﹣x≥0,且≥0,得≤x≤1.
.
由于,
所以当时,y2取到最大值1,故a=1.
当或1时,y2取到最小值,故.
所以:.
故答案为:.
16.解:∵当x2﹣4x+3=0时,x=1或x=3,
∴当x<1或x>3时,x2﹣4x+3>0,即:y=|x2﹣4x+3|,函数值大于0,
当1<x<3时,﹣1≤x2﹣4x+3<0,即:y=|﹣x2+4x﹣3|,函数最大值为1,
故符合条件的实数b的取值范围是0<b≤1.
17.解:配方得y=4(x﹣)2﹣2a+2,故函数图象开口朝上,且对称轴为x=.
当≤0,即a≤0时,当x=0时,y最小值=a2﹣2a+2=3,解得a=1﹣或a=1+(舍);
当0<<2,即0<a<4时,当x=时,y最小值=﹣2a+2=3,解得a=﹣(舍);
当≥2时,当x=2时,y最小值=8﹣8a+a2﹣2a+2=3,
解得a=5+.
综上所述,a的值是1﹣或5+.
故答案是:1﹣或5+.
18.解:联立方程组
,
消去y得,x2+(a+17)x+38﹣a=,
即x3+(a+17)x2+(38﹣a)x﹣56=0,
当x=1时,x3+(a+17)x2+(38﹣a)x﹣56=0,
∴式子x3+(a+17)x2+(38﹣a)x﹣56中含有因式(x﹣1),
分解因式得(x﹣1)[x2+(a+18)x+56]=0,(1)
显然x1=1是方程(1)的一个根,(1,56)是两个函数的图象的一个交点.
因为a是正整数,所以关于x的方程x2+(a+18)x+56=0,(2)
其判别式Δ=(a+18)2﹣224>0,它一定有两个不同的实数根.
而两个函数的图象的交点都是整点,所以方程(2)的根都是整数,
因此它的判别式Δ=(a+18)2﹣224应该是一个完全平方数.
设(a+18)2﹣224=k2(其中k为非负整数),则(a+18)2﹣k2=224,即(a+18+k)(a+18﹣k)=224.
显然a+18+k与a+18﹣k的奇偶性相同,且a+18+k≥18,而224=112×2=56×4=28×8,
所以
或或,
解得
或
或.
而a是正整数,所以只可能
或.
故答案为:a=39或a=12.
19.解:∵当x<2时,y随x的增大而减小.当x<2时,y>0.
∴可以写一个对称轴是直线x=2,开口向上的二次函数就可以.
∵函数的图象不经过第三象限.
∴所写的二次函数的顶点可以在x轴上方,
设顶点是(2,0),并且二次项系数大于0的二次函数,就满足条件.
如y=(x﹣2)2,答案不唯一.
故答案为:y=(x﹣2)2.
20.解:配方y=(x+a)2﹣1,
函数的对称轴为直线x=﹣a,
顶点坐标为(﹣a,﹣1).
①当0≤﹣a≤3即﹣3≤a≤0时,
函数最小值为﹣1,不合题意;
②当﹣a<0即a>0时,
∵当x=3时,y有最大值;当x=0时,y有最小值,
∴,解得a=2;
③当﹣a>3即a<﹣3时,
∵当x=3时,y有最小值;当x=0时,y有最大值,
∴,解得a=﹣5.
∴实数a的值为2或﹣5.
故答案为2或﹣5.
21.解:令y==6﹣,
问题转化为考虑函数z=x2+2x+2的最小值,
∵z=x2+2x+2=(x+1)2+1
∴当x=﹣1时,zmin=1,
∴ymin=6﹣2=4,
即分式分式的最小值是:4.
故答案为:4.
22.解:由题意,得:=±3,
当=3时,c=14,
当=﹣3时,c=8.
即c的值为14或8.
故答案为:14或8.
23.解:设t=2a﹣b,故b=2a﹣t,
∵a2+b2﹣2a﹣4=0,
∴a2+4a2﹣4at+t2﹣2a﹣4=0,
即5a2﹣(4t+2)a+t2﹣4=0,
Δ=(4t+2)2﹣20(t2﹣4)≥0,
解得﹣3≤t≤7,
故2a﹣b的最大值与最小值之差为7﹣(﹣3)=10.
故答案为10.
24.解:令x﹣1===k,则x=k+1,y=2k﹣1,z=3k+2,
于是x2+y2+z2=(k+1)2+(2k﹣1)2+(3k+2)2,
=k2+2k+1+4k2+1﹣4k+9k2+4+12k
=14k2+10k+6,
其最小值为==.
25.解:(1)把B(1,4)代入y=﹣x+m得,m=5,
∴直线的解析式为:y=﹣x+5,
∴A(4,1),
把A(4,1),B(1,4)代入y=﹣x2+bx+c得,,
解得:,
∴抛物线解析式为:y=﹣x2+4x+1;
(2)存在,
设P点坐标为(m,﹣m2+4m+1),
∵线段AB的中点E的坐标为(,),
∴直线OP的解析式为:y=x,
∴m=﹣m2+4m+1,
解得:m=或m=,
∴P点坐标为(,)(,).
26.解:(1)把A(﹣2,0)、B(4,0)、C(0,4)代入y=ax2+bx+c得,,
解得:,
∴该抛物线的解析式为:y=﹣x2+x+4;
(2)∵x=﹣=1,
∴D(1,0),
∵点E为对称轴上一点,
∴设E(1,m),
则DE=|m|,
∵将线段ED绕点E顺时针方向旋转90°得到线段EF,
∴∠FED=90°,EF=DE=|m|,
当点E在x轴的上面,
∴F(1﹣m,m),
∵点F恰好在该抛物线上,
∴m=﹣(1﹣m)2+(1﹣m)+4,
解得:m=﹣1+,m=﹣1﹣,(不合题意,舍去),
当点E在x轴的下面,
∴F(1﹣m,m),
∵点F恰好在该抛物线上,
∴m=﹣(1﹣m)2+1﹣m+4,
解得:m=﹣1+(舍弃),m=﹣1﹣,
∴线段DE的长为:﹣1或1+.
27.解:(1)由题意得,AM=t,ON=2t,则OM=OA﹣AM=18﹣t,
四边形ABNM的面积S=△AOB的面积﹣△MON的面积
=×18×30﹣×(18﹣t)×2t
=t2﹣18t+270(0<t≤15);
(2)S=t2﹣18t+270
=t2﹣18t+81﹣81+270
=(t﹣9)2+189,
∵a=1>0,
∴S有最小值,这个值是189.
28.解:∵抛物线y1=ax2+bx+c(a≠0,a≠c),经过A(1,0),
抛物线不过第三象限,则a>0,
把点代入函数即可得到:b=﹣a﹣c;
(1)由题意得:函数对称轴是直线x=2=,而a=1、b=﹣a﹣c,
解得:b=﹣4,c=3;
(2)由抛物线开口向上,且过点A,知:顶点在x轴下方,
即:<0;
(3)由韦达定理得:
x1+x2=,x1x2=,
其中x1=1,则x2=,而D坐标是(,b+8),
故:b+8=0,即b=﹣8,
∵a+c=﹣b,∴a+c=8…①,
把B、C两点代入直线解析式易得:c﹣a=4…②,
联立①、②并求解得:a=2,c=6
函数表达式为:y=2x2﹣8x+6,
A、B、C点的坐标分别为(1,0)、(2,﹣2)、(3,0)
当≤x<5时,
y1的取值范围易证为:16>y1≥﹣2,
同课章节目录
