1.1认识三角形 课件（共20张PPT）

(共22张PPT)
教学模板PPT
浙教版
八年级上
新知导入
那么，怎样的图形叫做三角形呢?
新知讲解
三角形的定义
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
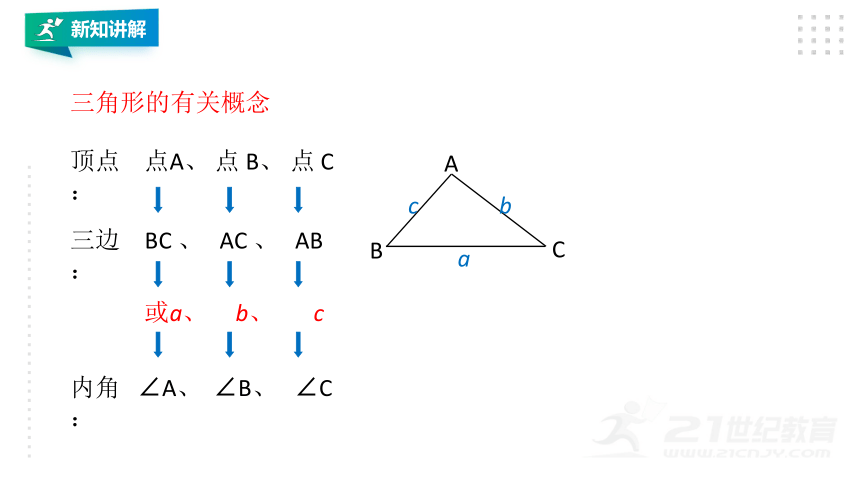
三角形的表示方法
“三角形”用符号“Δ”表示，如图顶点是A，B，C的三角形记做“ΔABC”，读做“三角形ABC”.
A
B
C
BC
、
AC
、
AB
内角：
∠A、
∠B、
∠C
点A、
点
B、
点
C
A
B
C
a
c
b
或a、
b、
c
三边：
顶点：
三角形的有关概念
新知讲解
课堂练习
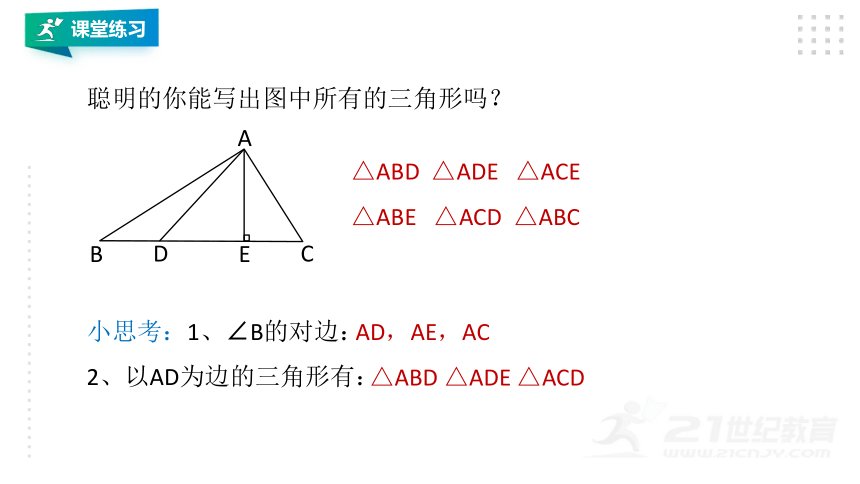
聪明的你能写出图中所有的三角形吗？
△ABD
△ADE
△ACE
△ABE
△ACD
△ABC
小思考：1、∠B的对边：
2、以AD为边的三角形有：
AD，AE，AC
△ABD
△ADE
△ACD
B
C
E
D
A
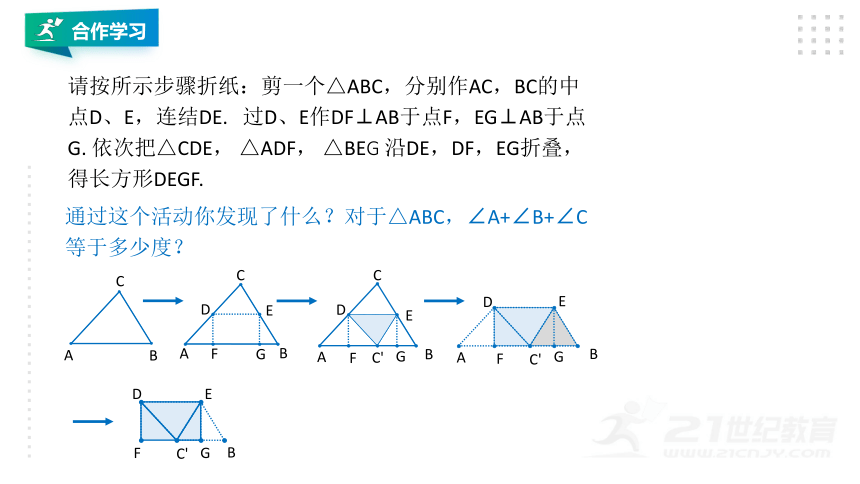
合作学习
请按所示步骤折纸：剪一个△ABC，分别作AC，BC的中点D、E，连结DE.
过D、E作DF⊥AB于点F，EG⊥AB于点G.
依次把△CDE，
△ADF，
△BEG
沿DE，DF，EG折叠，得长方形DEGF.
C
A
B
G
F
E
D
C
A
B
C'
G
F
E
D
C
A
B
C'
G
F
E
D
A
B
C'
G
F
E
D
B
通过这个活动你发现了什么？对于△ABC，∠A+∠B+∠C等于多少度？
新知讲解
A
B
C
三角形三个内角的和等于180°
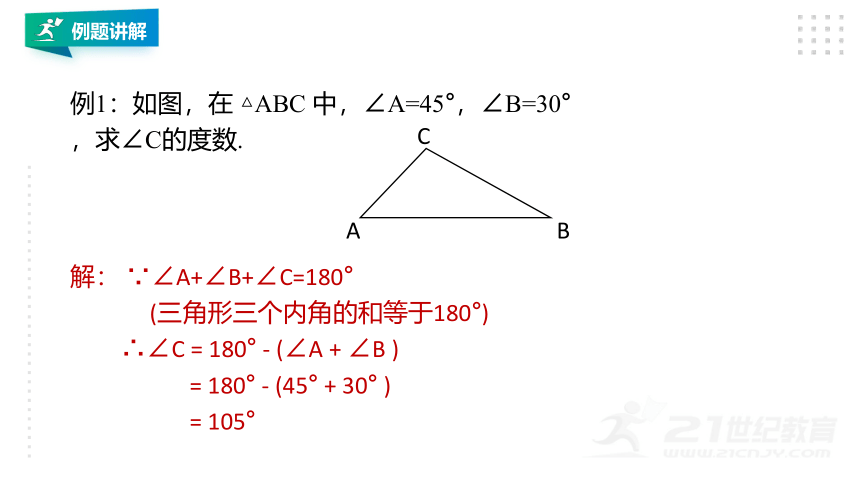
例1：如图，在
△ABC
中，∠A=45°，∠B=30°，求∠C的度数.
C
A
B
解：
∵∠A+∠B+∠C=180°
(三角形三个内角的和等于180°)
∴∠C
=
180°
-
(∠A
+
∠B
)
=
180°
-
(45°
+
30°
)
=
105°
例题讲解
变式1：在△ABC中，∠A=45°，∠B=2∠C，求∠B、
∠C的度数.
变式2：在△ABC中，∠A=∠B=2∠C，求∠B、
∠C的度数.
变式3：在△ABC中，∠A：∠B：∠C=2：3：5，求∠A
、∠B、∠C的度数.
变式4：在△ABC中，∠A+∠B
=∠C，求∠C的度数.
∠B=90°
∠C=45°
∠B=72°
∠C=36°
∠A=36°
∠B=54°
∠C=90°
∠C=90°
变式练习
一个三角形中：
最多有几个钝角？几个直角？几个锐角？
想一想：
钝角三角形
直角三角形
锐角三角形
A
B
C
A
B
C
A
B
C
三角形按内角的大小分类如下：
三角形
直角三角形（有一个直角）
锐角三角形（三个都是锐角）
钝角三角形（有一个钝角）
一个三角形有一个角是30
°，这个三角形是什么类型的三角形？
知识讲解
例2:
已知△ABC中，∠A∶∠B∶∠C=1∶3∶5，求∠A、∠B和∠C的度数，它是什么三角形？
解：∵
∠A∶∠B∶∠C=1∶3∶5，
且∠A+∠B+∠C=180°
设∠A=x
则∠B=3x
∠C=5x
.
即x
+
3x
+
5x
=
180°
∴
x
=20°
∴
∠A=
20°
，∠B=
60°
，∠C=
100°
△ABC为钝角三角形.
例题讲解
在△ABC中∠A：∠B：∠C＝1：2：3，则
△ABC是（
）
A.
锐角三角形
B.
直角三角形
C.
钝角三角形
D.
不能确定
B
课堂练习
A
B
●
②
③
①
④
上图由A地——B地，走那条路最近？为什么？
想一想
两点之间线段最短
任意两边之和大于第三边
A
B
C
a
b
c
两点之间线段最短！
从A到B走哪条路要近？为什么？
结论：
如何判断三条线段能否组成三角形?
例2：判断下列各组线段中，哪些能组成三角形，哪些不能组成三角形，并说明理由.
(1)
a
=
2.5cm，b
=
3cm，c
=
5cm.
(2)
e
=
6.3cm，f
=
6.3cm，g
=
12.6cm.
解
(1)
∵
最长线段是
c
=
5cm，a
+
b=2.5+3=5.5(cm)
∴
a
+
b＞c.
所以线段a，b，c能组成三角形.
(2)
∵
最长线段是g=12.6cm，e
+
f
=6.3+6.3=12.6(cm)
∴
e
+
f
=
g.所以线段e，f，g不能组成三角形.
例题讲解
长度为6cm，4cm，3cm三条线段能否组成三角形？
只要满足较小的两条线段之和大于较长线段，便可构成三角形；若不满足，则不能构成三角形.
判断方法：
(1)
找出较长边.
(2)
比较大小：较长边
较短两边之和.
(3)
判断能否组成三角形.
解:∵
6+4>3
6+3>4
4+3>6
∴能组成三角形
小于
课堂练习
三角形任何两边的差与第三边有什么关系？
三角形任何两边的差小于第三边
a
-
b
____
c；
b
-
c
____
a
；
c
-
a
____
b；
<
<
<
合作探究
课堂小结
1.
用符号、字母表示三角形.
2.
三角形的三边关系：
(1)判断三条已知线段能否组成三角形.
(2)已知三角形的两边，求第三边的取值范围：
两边之差
?
第三边
?
两边之和
三角形的任何两边的和大于第三边；两边之差小于第三边
作业布置
作业本
课本作业题1.2.6
https://www.21cnjy.com/help/help_extract.php